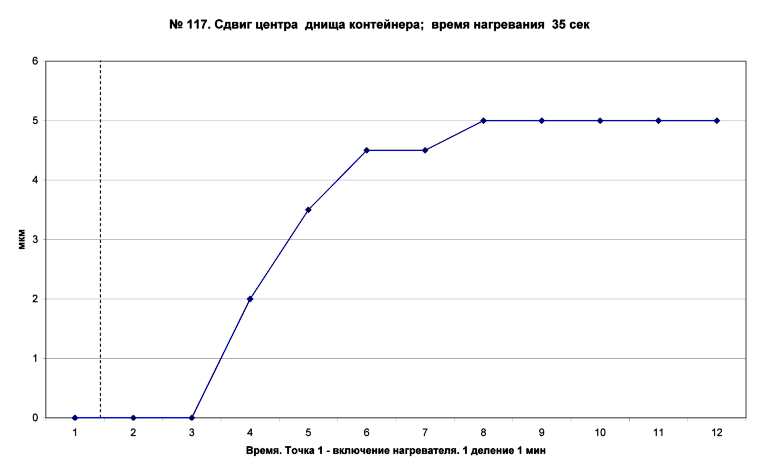
1. Степень герметичности контейнера оценивалась двумя способами. В первом измерялась деформация (прогиб) днища контейнера, вызванная изменением давления воздуха внутри сосуда. Прогиб днища контейнера, выполняющего роль мембраны “манометра”, контролировался с помощью механического индикатора смещений, а также оптическим методом (на центр мембраны опирался край легкого плоского зеркала, угловые смещения которого фиксировались с помощью луча лазера); оба метода показали одинаковые результаты. На рис. 1П и рис. 2П приведены временные зависимости величины прогиба мембраны, пропорциональные изменению давления внутри контейнера при обычном (35 с) и повышенном (180 с) временах нагрева образца.
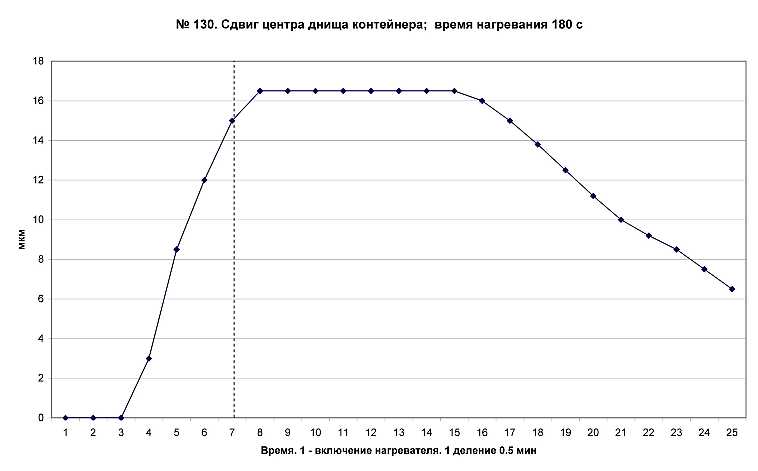
Сравнение временных зависимостей на рис. 1П и рис. 3 статьи, а также протяженное “плато” на рис. 2П, указывают, что герметичность контейнера достаточно высока и влияние утечки воздуха из контейнера на измерения температурной зависимости массы образца (рис. 3) незначительно.
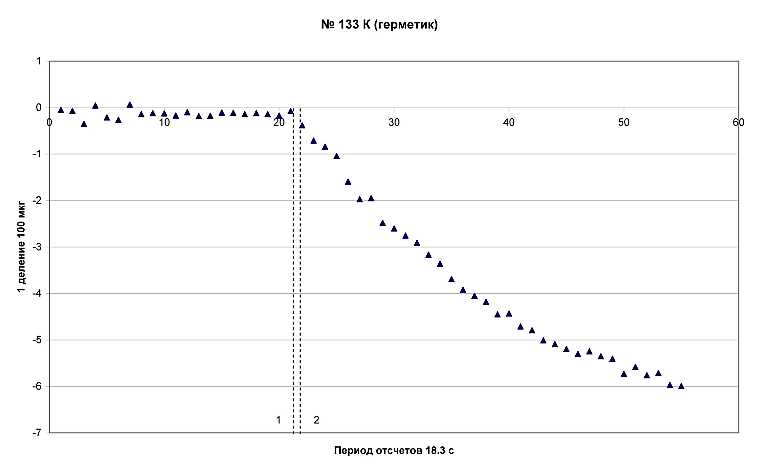
Во втором способе проверки герметичности контейнера его поверхность покрывалась толстым слоем полимерного клея “герметик”, после чего выполнялись измерения температурной зависимости веса образца по описанной в статье методике. Результаты таких измерений приведены на рис. 3П и хорошо соответствуют рис. 3 статьи.
2. Изменения объема контейнера, вызванные температурным ростом давления находящегося в нем воздуха, приводят к изменению величины его плавучести (архимедовой силы выталкивания). Для оценки влияния этого фактора на результаты взвешивания выполнены измерения температуры воздуха внутри контейнера, непосредственно у его боковых стенок, представленные на рис. 4П и рис. 5П.
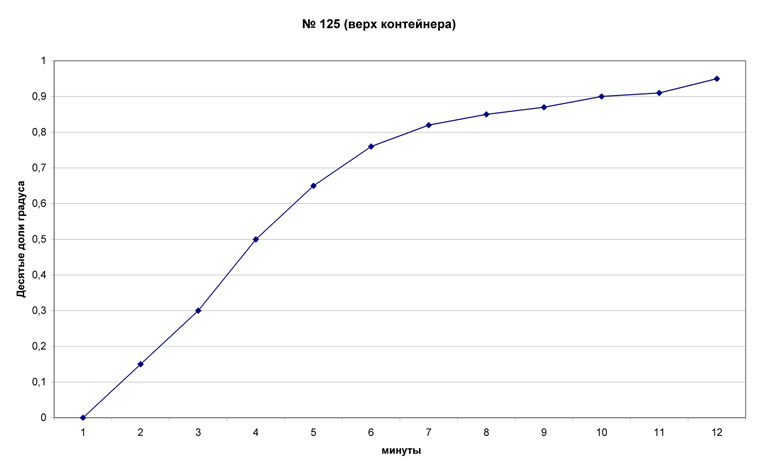
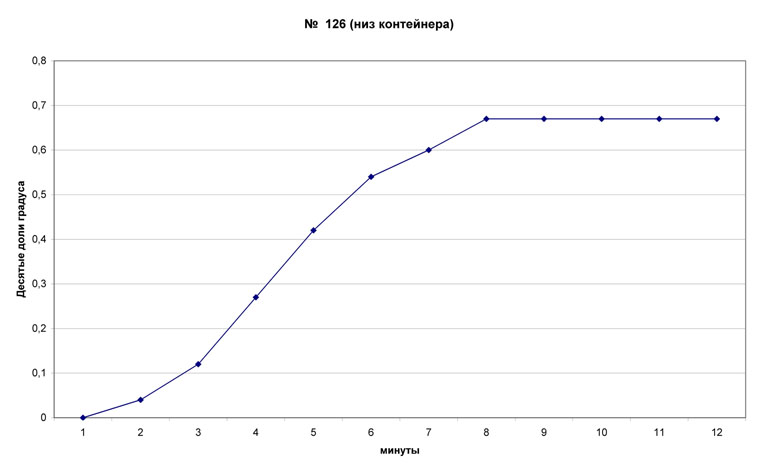
Распределение температуры в заполненном пористым теплоизолятором объеме контейнера неоднородно и на основании приводимых данных, с учетом указанной в статье оценки максимальной температуры нагреваемого образца, изменение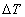 
средней температуры воздуха в объеме контейнера, по крайней мере, не превышает 3°К. Соответствующее максимальное изменение 
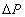давления в сосуде,
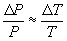, (1)где нормальное атмосферное давление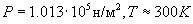 
, 
.
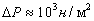Изменение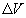 
объема контейнера равно сумме изменения 
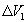объема его цилиндрической части и изменения 
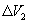объема, обусловленного деформацией его торцов. Согласно элементарной теории упругости,
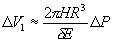, (2)где H - высота цилиндра,
R - его радиус,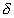 
- толщина стенок, E
- модуль Юнга материала цилиндра.
Подстановкой в выражение 2 величин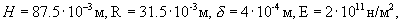 
получим 
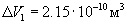. Соответствующее
отрицательное приращение кажущейся массы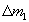 
контейнера, 
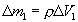(плотность воздуха
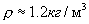) равно около 0.26 мкг, что в
условиях проводимого эксперимента, очевидно, несущественно. Гораздо большее
влияние на величину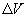 
оказывают деформации обоих торцов контейнера, при этом, полагая форму деформированного днища контейнера близкой к сферической,
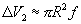, (3) где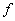 
- величина прогиба днища.
Подставляя в 3 экспериментальное максимальное значение прогиба днища величиной 5 мкм (рис. 1П), для
соответствующего изменения кажущейся массы контейнера вследствие деформации торцов контейнера, находим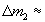
20 мкг.
Экспериментально наблюдаемое изменение массы контейнера (рис. 3 статьи, рис 3П) примерно в 30 раз превышает приведенную оценку. Итак, есть серьезные основания полагать, что основной причиной изменения кажущейся массы контейнера, рассмотренного в настоящей статье и подтверждаемого другими независимыми экспериментами, является отрицательная температурная зависимость силы тяжести.
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
