Ответственное занятие, от которого будет зависеть Ваш успех в освоении основ программирования. Причем, не только на QB. Внимательно отнеситесь к изучению стандартных функций, постарайтесь выработать навык безошибочного набора математических формул.
Вам известны функции, изученные и изучаемые в курсе математики и других дисциплин. Как задаются и вычисляются их значения на языках программирования?
Вначале рассмотрим хорошо Вам известные из математики функции: Sinx, Cosx, tgx, arctgx, ç х ç
На QB эти функции записываются в весьма естественном виде:
a = SIN(x): m = COS(t): n = TAN(q)
y = ATN(p):’*****это функция arctgx*****
Если аргументам x, t, q, p, были присвоены какие-либо значения, то переменным a, m, n, y будут присвоены значения указанных функций. Обратите внимание, что аргументы всех функций на QB пишутся только в скобках. Аргументы тригонометрических функций не градусы, а действительные числа (обратите внимание!). В качестве аргументов могут быть действительные числа, так строка r = SIN(2) присвоит переменной r значение синуса действительного числа 2. Написание на QB всех функций осуществляйте только строчными буквами и если Вы сделали правильно QB сам “сделает” их заглавными.
Почему мы на прошлом занятии записали pi = 4*ATN(1)? Так мы присвоили переменной pi значение 3.1415926.. Вам хорошо известно, что arctg1 = ![]() .
.
ç х ç - часто используемый модуль числа, на QB это ABS(x), почему-то студенты часто ошибаются и пишут АВС (?).
y = ex, (ее график называют экспонентой, часто и саму функцию) – популярнейшая функция, многие процессы и явления изменяются именно по этому закону. На QB (и на других языках) это EXP(x).
Попросите QB ? EXP(1) и Вы увидите знакомое Вам значение 2.718281828..
А возведение в степень переменных, констант осуществляется с помощью знака “^”. Набирают x^2 (это x2), a^(x/2) и т.д. Никогда не набирайте EXP^x - плохая ошибка!
Логарифмическая функция. QB “знает” только натуральный логарифм – lnx. И набирают LOG(x). Если необходимо найти логарифм по произвольному основанию a, то используют формулу перехода: LOG(x)/LOG(a)
Функция y = ![]() . На QB это SQR(x), а вот корни произвольной степени придется записывать так:
. На QB это SQR(x), а вот корни произвольной степени придется записывать так: ![]() Þ x^(3/4), что не одно и то же, что x^3/4, подумайте почему (!).
Þ x^(3/4), что не одно и то же, что x^3/4, подумайте почему (!).
Особое внимание уделим функциям, которые редко используются в традиционной математике, но довольно популярны в программировании.
Функция SGN(x) – знак числа, она принимает только 3 значения: 1, если х > 0, -1, если х < 0 и 0, если ее аргумент равен нулю.
Функция MOD. x = a MOD(3) – эта конструкция означает, что переменной х присваивается значение равное остатку от деления целой части числа а на 3, в дальнейшем эта конструкция может использоваться в качестве признака деления. Аргументом в скобках может быть и переменная.
Очень популярная в программировании функция, которой мы будем часто пользоваться, функция RND. Кстати, на Ваших МК есть такая кнопочка. Функция генерирует случайные числа из интервала (0; 1)
На самом деле числа псевдослучайные, т.е. при каждом запуске получают одни и те же значения. Чтобы сделать их “более случайными” каждая программа, использующая RND, снабжается строкой RANDOMIZE TIMER, этот оператор “запускает” генератор случайных чисел. См. предыдущее занятие.
Часто необходимо сгенерировать случайные числа из заданного интервала (a;b). Согласитесь с конструкцией: x = a + (b – a)*RND. Переменная х получит значение, принадлежащее интервалу (a;b).
Более подробно остановиться на функциях INT и CINT.
Функция INT(x) – целая часть числа х, причем – это ближайшее целое число, стоящее на числовой прямой слева от х. Естественно y = x - INT(x) – это дробная часть числа. Функция же СINT(x) округляет число х до ближайшего целого. (Предлагаем студентам самостоятельно изучить аналогичную функцию FIX.) В силу того, что CINT имеет ограничения по значениям аргумента, рекомендовать использовать функцию INT(x). Полезно здесь же научить округлять с заданной точностью, например:
х = 7.45632 x = (INT(x*100+.5))/100, при этом переменной х будет присвоено значение 7.46. Если х = 7.45332, то округленному до сотых долей х будет присвоено значение 7.45. Или x = (СINT(x*100))/100.
Еще примеры применения INT(x). Пусть переменной х пользователь присвоил или получил в результате вычислений значение угла в радианах: х = 2.45378. Перевести в градусы и минуты (QB “не знает” этой меры углов).
y = 180*2.45378/pi – это угол в градусах с десятичными долями.
yg = INT(y) – это целое число градусов,
ym = (СINT((y – yg)*60*100))/100 – это целое число минут.
И выводите на печать значения переменных yg и ym.
Обратный перевод: g – целое число градусов, m – целое число минут. Получить радианную меру этого угла. x = (g + m*60)*pi/180.
Используя приведенные примеры перевести самостоятельно в рубли и копейки сумму, выраженную десятичной дробью, например, х = 45.67854 рублей. Получить ответ: “С Вас 45 рублей и 68 копеек”.
Функция пользователя, оператор DEF FN_, где _ - идентификатор – какая-либо буква латинского алфавита. Отметим, что DEF FN может задавать функции более чем одной переменной, что его задание должно обязательно предшествовать первому обращению к нему, что программа может содержать несколько функций пользователя, отличающихся идентификатором, т.е. не более 26. Например:
DEF FNA(x) = x^2 – 5*x + 3
DEF FNB(x,y) = y*x^2 – y^3*x + 3*y*x – SIN(2*x) и т.д.
Теперь, используя полученную информацию, необходимо выработать устойчивые навыки по набору математических выражений. Учимся набирать на QB формулы:
Пусть необходимо вычислить значение функции
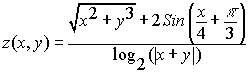
****************Программа 3.1**********************************
INPUT”Введите х и у”; x,y
z = (SQR(x^2 + y^2) + 2*SIN(x/4 + pi/3))/((LOG(ABS(x + y))/LOG(2))
PRINT “z = “;z
Будьте внимательны при использовании скобок – “золотое правило”: сколько скобок открыто, столько же должно быть закрыто. При наборе дробей помните: ВЕСЬ числитель делится, как правило, на ВЕСЬ знаменатель, не забывайте о скобках.
Рекомендуется работать в режиме строчных латинских букв, это очень полезно – сам QB будет проверять правильность набора. Например, так.
****************Программа 3.2**********************************
input”Введите a и b”;a,b
t=((cos(a+b))^2-log(a*b)/log(2))/(a+sqr(a^2+b^2))/abs(a+b)
?”Получите t=”;t
Посмотрите, что сделал с набранной программой QB.
А теперь восстановите набранную формулу: запишите ее на языке обычной алгебры.
Пусть необходимо вычислить значение выражения, зависящего от двух переменных. Некоторые студенты во избежание ошибок “разбивают” эту формулу на отдельные части.
 ;
;
****************Программа 3.3**********************************
INPUT”Введите х и у”; x,y
t = sin(x) + (x + y)^2
p = sqr(x^2 + y^2)
q = (exp(x) + atn(x))^(1/3)
?”Получите m”; t/(p + q)
Чтобы научиться программировать формулы, их надо программировать, проверять у QB, консультироваться с товарищами, проверять у преподавателя, только не словами: “Найдите у меня ошибку”…
В качестве домашнего задания запрограммируйте несколько формул: готовьтесь к самостоятельной работе!
 ;
; 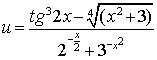
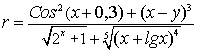 ;
; 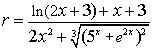
Что нового Вы узнали и чему научились?
|
|