Статистика нечисловых данных - это направление в эконометрике, в котором в качестве исходных статистических данных (результатов наблюдений) рассматриваются объекты нечисловой природы. Так принято называть объекты, которые нецелесообразно описывать числами, в частности элементы нелинейных пространств. Примерами являются бинарные отношения (ранжировки, разбиения, толерантности и др.), результаты парных и множественных сравнений, множества, нечеткие множества, измерение в шкалах, отличных от абсолютных. Этот перечень примеров не претендует на законченность. Он складывался постепенно в соответствии с развитием теоретических исследований в области статистики нечисловых данных и расширением опыта применений этого направления эконометрики.
Объекты нечисловой природы широко используются в теоретических и прикладных исследованиях по экономике, менеджменту и другим проблемам управления, в частности управления качеством продукции, в технических науках, социологии, психологии, медицине и т.д., а также практически во всех отраслях народного хозяйства.
8.1. Объекты нечисловой природы
Начнем с первоначального знакомства с основными видами объектов нечисловой природы.
Результаты измерений в шкалах, отличных от абсолютной. Рассмотрим конкретное исследование в области маркетинга образовательных услуг, послужившее поводом к развитию отечественных исследований по теории измерений (см. главу 3). При изучении привлекательности различных профессий для выпускников новосибирских школ был составлен список из 30 профессий. Опрашиваемых просили оценить каждую из этих профессий одним из баллов 1,2,...,10 по правилу: чем больше нравится, тем выше балл. Для получения социологических выводов необходимо было дать единую оценку привлекательности определенной профессии для совокупности выпускников школ. В качестве такой оценки в работе [1] использовалось среднее арифметическое баллов, выставленных профессии опрошенными школьниками. В частности, физика получила средний балл 7,69, а математика - 7,50. Поскольку 7,69 больше, чем 7,50, был сделан вывод, что физика более предпочтительна для школьников, чем математика.
Однако этот вывод противоречит данным работы [2], согласно которым ленинградские школьники средних классов больше любят математику, чем физику. Обсудим одно из возможных объяснений этого противоречия, которое сводится к указанию на неадекватность (с точки зрения теории измерений) методики обработки эконометрических данных, примененной в работе [1].
Дело
в том, что баллы 1,2,...,10 введены конкретными исследователями, т.е.
субъективно. Если одна профессия оценена в 10 баллов, а вторая - в 2, то из
этого нельзя заключить, что первая ровно в 5 раз привлекательней второй. Другой
коллектив социологов мог бы принять иную систему баллов, например 1,4,9,16,...,100.
Естественно предположить , что упорядочивание профессий по привлекательности,
присущее школьникам, не зависит от того, какой системой баллов им предложит
пользоваться маркетолог. Раз так, то распределение профессий по градациям
десятибалльной системы не изменится, если перейти к другой системе баллов с
помощью любого допустимого преобразования в порядковой шкале (см. главу 3),
т.е. с помощью строго возрастающей функции ![]() Если , Y1, Y2,...,Yn -ответы
n выпускников школ, касающихся математики, а Z1,
Z2,...,Zn -физики,
то после перехода к новой системе баллов ответы относительно математики будут
иметь вид g(Y1), g(Y2),...,g(Yn), а относительно физики - g(Z1), g(Z2),...,g(Zn).
Если , Y1, Y2,...,Yn -ответы
n выпускников школ, касающихся математики, а Z1,
Z2,...,Zn -физики,
то после перехода к новой системе баллов ответы относительно математики будут
иметь вид g(Y1), g(Y2),...,g(Yn), а относительно физики - g(Z1), g(Z2),...,g(Zn).
Пусть
единая оценка привлекательности профессии вычисляется с помощью функции f(X1, X2,...,Xn). Какие требования естественно наложить на
функцию ![]() чтобы полученные с ее помощью выводы не
зависели от того, какой именно системой баллов пользовался специалист по
маркетингу образовательных услуг?
чтобы полученные с ее помощью выводы не
зависели от того, какой именно системой баллов пользовался специалист по
маркетингу образовательных услуг?
Замечание. Обсуждение можно вести в терминах экспертных оценок. Тогда вместо сравнения математики и физики n экспертов (а не выпускников школ) оценивают по конкурентоспособности на мировом рынке, например, две марки стали. Однако в настоящее время маркетинговые и социологические исследования более привычны, чем экспертные.
Единая оценка вычислялась для того, чтобы сравнивать профессии по привлекательности. Пусть f(X1, X2,...,Xn) - среднее по Коши. Пусть среднее по первой совокупности меньше среднего по второй совокупности:
f(Y1, Y2,...,Yn) < f(Z1, Z2,...,Zn ).
Тогда согласно теории измерений (см. главу 3) необходимо потребовать, чтобы для любого допустимого преобразования g из группы допустимых преобразований в порядковой шкале было справедливо также неравенство
f(g(Y1), g(Y2),...,g(Yn)) < f(g(Z1), g(Z2),...,g(Zn)).
т.е. среднее преобразованных значений из первой совокупности также было меньше среднего преобразованных значений для второй совокупности. Причем сформулированное условие должно быть верно для любых двух совокупностей Y1, Y2,...,Yn и Z1, Z2,...,Zn и, напомним, любого допустимого преобразования. Средние величины, удовлетворяющие сформулированному условию, называют допустимыми (в порядковой шкале). Согласно теории измерений только такими средними можно пользоваться при анализе мнений выпускников школ, экспертов и иных данных, измеренных в порядковой шкале.
Какие единые оценки привлекательности профессий f(X1, X2,...,Xn) устойчивы относительно сравнения? Ответ на этот вопрос дан в главе 3. В частности, оказалось, что средним арифметическим, как в работе [1] новосибирских специалистов по маркетингу образовательных услуг, пользоваться нельзя, а порядковыми статистиками, т.е. членами вариационного ряда (и только ими) - можно.
Методы анализа конкретных экономических данных, измеренных в шкалах, отличных от абсолютной, являются предметом изучения в статистике нечисловых данных как части эконометрики. Как известно, основные шкалы измерения делятся на качественные (шкалы наименований и порядка) и количественные (шкалы интервалов, отношений, разностей, абсолютная). Методы анализа статистических данных в количественных шкалах сравнительно мало отличаются от таковых в абсолютной шкале. Добавляется только требование инвариантности относительно преобразований сдвига и/или масштаба. Методы анализа качественных данных - принципиально иные. О них пойдет речь в настоящей главе.
Напомним,
что исходным понятием теории измерений является совокупность ![]() допустимых преобразований шкалы (обычно
Ф- группа),
допустимых преобразований шкалы (обычно
Ф- группа), ![]() . Алгоритм обработки данных W, т.е. функция
. Алгоритм обработки данных W, т.е. функция ![]() (здесь A-множество возможных результатов работы алгоритма)
называется адекватным в шкале с совокупностью допустимых преобразований Ф, если
(здесь A-множество возможных результатов работы алгоритма)
называется адекватным в шкале с совокупностью допустимых преобразований Ф, если
![]()
для
всех ![]() и всех
и всех ![]() Таким образом, теорию измерений
рассматриваем как теорию инвариантов относительно различных совокупностей
допустимых преобразований Ф. Интерес вызывают две задачи:
Таким образом, теорию измерений
рассматриваем как теорию инвариантов относительно различных совокупностей
допустимых преобразований Ф. Интерес вызывают две задачи:
а) дана группа допустимых преобразований Ф (т.е. задана шкала); какие алгоритмы анализа данных W из определенного класса являются адекватными?
б) дан алгоритм анализа данных W; для каких шкал (т.е. групп допустимых преобразований Ф) он является адекватным?
В главе 3 первая задача рассматривалась для алгоритмов расчета средних величин. Информацию о других результатах решения задач указанных типов можно найти в работах [3-5].
Бинарные отношения. Пусть ![]() - адекватный алгоритм в шкале
наименований. Можно показать, что этот алгоритм задается некоторой функцией от
матрицы
- адекватный алгоритм в шкале
наименований. Можно показать, что этот алгоритм задается некоторой функцией от
матрицы ![]() где
где
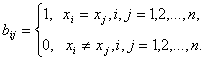
Если
![]() - адекватный алгоритм в шкале порядка,
то этот алгоритм задается некоторой функцией от матрицы
- адекватный алгоритм в шкале порядка,
то этот алгоритм задается некоторой функцией от матрицы ![]() порядка n
порядка n ![]() n, где
n, где
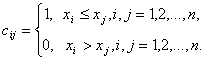
Матрицы
B и C можно проинтерпретировать в терминах бинарных отношений.
Пусть некоторая характеристика измеряется у n объектов q1,q2,…,qn, причем xi - результат ее измерения у объекта qi Тогда матрицы B и C задают
бинарные отношения на множестве объектов Q ={q1,q2,…,qn}. Поскольку бинарное отношение можно
рассматривать как подмножество декартова квадрата Q ![]() Q, то любой матрице D = ||dij|| порядка n
Q, то любой матрице D = ||dij|| порядка n ![]() n из 0 и 1 соответствует бинарное отношение R(D),
определяемое следующим образом:
n из 0 и 1 соответствует бинарное отношение R(D),
определяемое следующим образом: ![]() тогда и только тогда, когда dij = 1.
тогда и только тогда, когда dij = 1.
Бинарное
отношение R(B) - отношение эквивалентности, т.е. рефлексивное
симметричное транзитивное отношение. Оно задает разбиение Q на классы
эквивалентности. Два объекта qi
и qj входят в один класс эквивалентности тогда
и только тогда, когда ![]()
Выше показано, как разбиения возникают в результате измерений в шкале наименований. Разбиения могут появляться и непосредственно. Так, при оценке качества промышленной продукции эксперты дают разбиение показателей качества на группы. Для изучения психологического состояния людей их просят разбить предъявленные рисунки на группы сходных между собой. Аналогичная методика применяется и в иных экспериментальных психологических исследованиях, необходимых для оптимизации управления персоналом.
Во многих эконометрических задачах разбиения получаются "на выходе" (например, в кластер - анализе) или же используются на промежуточных этапах анализа данных (например, сначала проводят классификацию с целью выделения однородных групп, а затем в каждой группе строят регрессионную зависимость).
Бинарное
отношение R(С) задает разбиение Q на классы эквивалентности,
между которыми введено отношение строгого порядка. Два объекта qi и qj входят в один класс тогда и только
тогда, когда cij= 1 и cji= 1, т.е. xi = xj. Класс эквивалентности Q1 предшествует классу эквивалентности Q2 тогда и только тогда, когда для любых ![]() имеем cij = 1, cji= 0, т.е. xi < xj. Такое бинарное отношение в статистике часто называют
ранжировкой со связями; связанными считаются объекты, входящие в один класс
эквивалентности. В литературе встречаются и другие названия: линейный
квазипорядок, упорядочение, квазисерия, ранжирование. Если каждый из классов
эквивалентности состоит только из одного элемента, то имеем обычную ранжировку (другими
словами, линейный порядок).
имеем cij = 1, cji= 0, т.е. xi < xj. Такое бинарное отношение в статистике часто называют
ранжировкой со связями; связанными считаются объекты, входящие в один класс
эквивалентности. В литературе встречаются и другие названия: линейный
квазипорядок, упорядочение, квазисерия, ранжирование. Если каждый из классов
эквивалентности состоит только из одного элемента, то имеем обычную ранжировку (другими
словами, линейный порядок).
Как известно, ранжировки возникают в результате измерений в порядковой шкале. Так, при описанном выше опросе ответ выпускника школы - это ранжировка (со связями) профессий по привлекательности. Ранжировки часто возникают и непосредственно, без промежуточного этапа - приписывания объектам квазичисловых оценок - баллов. Многочисленные примеры тому даны М. Кендэлом [6]. При оценке качества промышленной продукции нормативные методические документы предусматривают использование ранжировок.
Для прикладных областей, кроме ранжировок и разбиений, представляют интерес толерантности, т.е. рефлексивные симметричные отношения. Толерантность - математическая модель для выражения представлений о сходстве (похожести, близости). Разбиения - частный вид толерантностей. Толерантность, обладающая свойством транзитивности - это разбиение. Однако в общем случае толерантность не обязана быть транзитивной. Толерантности появляются во многих постановках теории экспертных оценок, например, как результат парных сравнений (см. ниже).
Напомним, что любое бинарное отношение на конечном множестве может быть описано матрицей из 0 и 1.
Дихотомические (бинарные) данные. Это данные, которые могут принимать одно из двух значений (0 или 1), т.е. результаты измерений значений альтернативного признака. Как уже было показано, измерения в шкале наименований и порядковой шкале приводят к бинарным отношениям, а те могут быть выражены как результаты измерений по нескольким альтернативным признакам, соответствующим элементам матриц, описывающих отношения. Дихотомические данные возникают в прикладных исследованиях и многими иными путями.
В настоящее время в большинстве стандартов на конкретную продукцию предусмотрен контроль по альтернативному признаку. Это означает, что единица продукции относится к одной из двух категорий - "годных" или "дефектных", т.е. соответствующих или не соответствующих требованиям стандарта. Отечественными специалистами проведены обширные теоретические исследования проблем статистического приемочного контроля по альтернативному признаку. Основополагающими в этой области являются работы академика А.Н.Колмогорова. Подход советской вероятностно-статистической школы к проблемам контроля качества продукции отражен в монографиях [7,8] (см. также главу 13).
Дихотомические данные - давний объект математической статистики. Особенно большое применение они имеют в экономических и социологических исследованиях, в которых большинство переменных, интересующих специалистов, измеряется по качественным шкалам. При этом дихотомические данные зачастую являются более адекватными, чем результаты измерений по методикам, использующим большее число градаций. В частности, психологические тесты типа MMPI используют только дихотомические данные. На них опираются и популярные в технико-экономическом анализе методы парных сравнений [9].
Элементарным актом в методе парных сравнений является предъявление эксперту для сравнения двух объектов (сравнение может проводиться также прибором). В одних постановках эксперт должен выбрать из двух объектов лучший по качеству, в других - ответить, похожи объекты или нет. В обоих случаях ответ эксперта можно выразить одной из двух цифр (меток)- 0 или 1. В первой постановке: 0, если лучшим объявлен первый объект; 1 - если второй. Во второй постановке: 0, если объекты похожи, схожи, близки; 1 - в противном случае.
Подводя итоги изложенному, можно сказать, что рассмотренные выше данные представимы в виде векторов из 0 и 1 (при этом матрицы, очевидно, могут быть записаны в виде векторов). Поскольку все результаты наблюдений имеют лишь несколько значащих цифр, то, используя двоичную систему счисления, любые виды анализируемых эконометрическими методами данных можно записать в виде векторов из 0 и 1. Представляется, что эта возможность имеет лишь академический интерес, но во всяком случае можно констатировать, что анализ дихотомических данных необходим во многих прикладных постановках.
Множества. Совокупность Xn векторов X = (x1, x2,…,xn) из 0 и 1 размерности n находится во
взаимно-однозначном соответствии с совокупностью 2n всех подмножеств множества N = {1, 2,
..., n}. При этом вектору X = (x1, x2,…,xn) соответствует подмножество N(X)![]() N, состоящее из тех и только из тех i, для которых xi = 1. Это объясняет, почему изложение
вероятностных и статистических результатов, относящихся к анализу данных,
являющихся объектами нечисловой природы перечисленных выше видов, можно вести
на языке конечных случайных множеств, как это было сделано в монографии .[3].
N, состоящее из тех и только из тех i, для которых xi = 1. Это объясняет, почему изложение
вероятностных и статистических результатов, относящихся к анализу данных,
являющихся объектами нечисловой природы перечисленных выше видов, можно вести
на языке конечных случайных множеств, как это было сделано в монографии .[3].
Множества как исходные данные появляются и в иных постановках. Из геологических реалий исходил Ж. Матерон, из электротехнических - Н.Н. Ляшенко и др. Случайные множества применялись для описания процесса случайного распространения, например распространения информации, слухов, эпидемии или пожара, а также в математической экономике. В монографии [3] рассмотрены приложения случайных множеств в теории экспертных оценок и в теории управления запасами и ресурсами (логистике).
Отметим, что реальные объекты можно моделировать случайными множествами как из конечного числа элементов, так и из бесконечного, однако при расчетах на ЭВМ неизбежна дискретизация, т.е. переход к первой из названных возможностей.
Нечеткие множества. Пусть A - некоторое множество. Подмножество B множества A характеризуется своей характеристической функцией
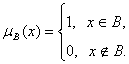 (1)
(1)
Что
такое нечеткое множество? Обычно говорят, что нечеткое подмножество C множества A характеризуется своей функцией принадлежности ![]() Если функция принадлежности
Если функция принадлежности ![]() имеет вид (1) при некотором B, то C есть обычное (четкое) подмножество A.
имеет вид (1) при некотором B, то C есть обычное (четкое) подмножество A.
Обычное подмножество можно было бы отождествить с его характеристической функцией. Этого математики не делают, поскольку для задания функции (в ныне принятом подходе) необходимо сначала задать множество. Нечеткое же подмножество с формальной точки зрения можно отождествить с его функцией принадлежности. Однако термин "нечеткое подмножество" предпочтительнее при построении математических моделей реальных явлений.
Начало современной теории нечеткости положено работой 1965 г. американского ученого азербайджанского происхождения Л.А.Заде. К настоящему времени по этой теории опубликованы тысячи книг и статей, издается несколько международных журналов, выполнено достаточно много как теоретических, так и прикладных работ.
Л.А. Заде рассматривал теорию нечетких множеств как аппарат анализа и моделирования гуманистических систем, т.е. систем, в которых участвует человек. Его подход опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от "принадлежности" к "непринадлежности" не скачкообразен, а непрерывен. В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятием, качеством продукции и технологическими процессами.
Л.А. Заде использовал термин "fuzzy set" (нечеткое множество). На русский язык термин "fuzzy" переводили как нечеткий, размытый, расплывчатый, и даже как пушистый и туманный.
Аппарат
теории нечеткости громоздок. В качестве примера дадим определения
теоретико-множественных операций над нечеткими множествами. Пусть C и D- два нечетких подмножества A с функциями принадлежности ![]() и
и ![]() соответственно. Пересечением
соответственно. Пересечением ![]() , произведением CD, объединением
, произведением CD, объединением ![]() , отрицанием
, отрицанием ![]() , суммой C+D называются нечеткие подмножества A с функциями принадлежности
, суммой C+D называются нечеткие подмножества A с функциями принадлежности
![]()
![]()
![]()
соответственно.
Теория нечетких множеств в определенном смысле сводится к теории вероятностей, а именно, к теории случайных множеств. Соответствующий цикл теорем приведен в книгах [3,10]. Однако при решении прикладных задач вероятностно-статистические методы и методы теории нечеткости обычно рассматриваются как различные.
Объекты нечисловой природы как статистические данные. В эконометрике и прикладной математической статистике наиболее распространенный объект изучения - выборка x1, x2,…,xn, т.е. совокупность результатов n наблюдений. В различных областях статистики результат наблюдения - это или число, или конечномерный вектор, или функция... Соответственно проводится деление прикладной математической статистики: одномерная статистика, многомерный статистический анализ, статистика временных рядов и случайных процессов... В статистике нечисловых данных в качестве результатов наблюдений рассматриваются объекты нечисловой природы, в частности, перечисленных выше видов - измерения в шкалах, отличных от абсолютной, бинарные отношения, вектора из 0 и 1, множества, нечеткие множества. Выборка может состоять из n ранжировок или n толерантностей, или n множеств, или n нечетких множеств и т.д.
Отметим необходимость развития методов статистической обработка "разнотипных данных", обусловленную большой ролью в прикладных исследованиях "признаков смешанной природы". Речь идет о том, что результат наблюдения состояния объекта зачастую представляет собой вектор, у которого часть координат измерена по шкале наименований, часть - по порядковой шкале, часть - по шкале интервалов и т.д. Статистические методы ориентированы обычно либо на абсолютную шкалу, либо на шкалу наименований (анализ таблиц сопряженности), а потому зачастую непригодны для обработки разнотипных данных. Есть и более сложные модели разнотипных данных, например, когда некоторые координаты вектора наблюдений описываются нечеткими множествами.
Для обозначения подобных неклассических результатов наблюдений в 1979 г. в монографии [3] предложен собирательный термин - объекты нечисловой природы. Термин "нечисловой" означает, что структура пространства, в котором лежат результаты наблюдений, не является структурой действительных чисел, векторов или функций, она вообще не является структурой линейного (векторного) пространства. При расчетах объекты числовой природы, разумеется, изображаются с помощью чисел, но эти числа нельзя складывать и умножать.
С целью "стандартизации математических орудий" целесообразно разрабатывать методы статистического анализа данных, пригодные одновременно для всех перечисленных выше видов результатов наблюдений. Кроме того, в процессе развития прикладных исследований выявляется необходимость использования новых видов объектов нечисловой природы, отличных от рассмотренных выше, например, в связи с развитием статистических методов обработки текстовой информации. Поэтому целесообразно ввести еще один вид объектов нечисловой природы - объекты произвольной природы, т.е. элементы множества, на которые не наложено никаких условий (кроме "условий регулярности", необходимых для справедливости доказываемых теорем). Другими словами, в этом случае предполагается, что результаты наблюдений (элементы выборки) лежат в произвольном пространстве X. Для получения теорем необходимо потребовать, чтобы X удовлетворяло некоторым условиям, например, было так называемым топологическим пространством. Как известно, ряд результатов классической математической статистики получен именно в такой постановке. Так, при изучении оценок максимального правдоподобия элементы выборки могут лежать в пространстве произвольной природы. Это не влияет на рассуждения, поскольку в них рассматривается лишь зависимость плотности вероятности от параметра. Методы классификации, использующие лишь расстояние между классифицируемыми объектами, могут применяться к совокупностям объектов произвольной природы, лишь бы в пространстве, где они лежат, была задана метрика. Цель статистики нечисловых данных (в некоторых литературных источниках используется термин "статистика объектов нечисловой природы") состоит в том, чтобы систематически рассматривать методы статистической обработки данных как произвольной природы, так и относящихся к указанным выше конкретным видам объектов нечисловой природы, т.е. методы описания данных, оценивания и проверки гипотез. Взгляд с общей точки зрения позволяет получить новые результаты и в других областях эконометрики.
Использование объектов нечисловой природы при формировании математической модели реального явления. Использование объектов нечисловой природы часто порождено желанием обрабатывать более объективную, более освобожденную от погрешностей информацию. Как показали многочисленные опыты, человек более правильно (и с меньшими затруднениями) отвечает на вопросы качественного например, сравнительного, характера, чем количественного. Так, ему легче сказать, какая из двух гирь тяжелее, чем указать их примерный вес в граммах. Другими словами, использование объектов нечисловой природы - средство повысить устойчивость эконометрических и экономико-математических моделей реальных явлений. Сначала конкретные области статистики объектов нечисловой природы (а именно, прикладная теория измерений, нечеткие и случайные множества) были рассмотрены в монографии [3] как частные постановки проблемы устойчивости математических моделей социально-экономических явлений и процессов к допустимым отклонениям исходных данных и предпосылок модели, а затем была понята необходимость проведения работ по развитию статистики объектов нечисловой природы как самостоятельного научного направления.
Начнем
со шкал измерения. Науку о единстве мер и точности измерений называют
метрологией. Таким образом, репрезентативная теория измерений - часть
метрологии. Методы обработки данных должны быть адекватны относительно
допустимых преобразований шкал измерения в смысле репрезентативной теории
измерений. Однако установление типа шкалы, т.е. задание группы преобразований ![]() - дело
специалиста соответствующей прикладной области. Так, оценки привлекательности
профессий мы считали измеренными в порядковой шкале. Однако отдельные социологи
не соглашались с этим, считая, что выпускники школ пользуются шкалой с более
узкой группой допустимых преобразований, например, интервальной шкалой.
Очевидно, эта проблема относится не к математике, а к наукам о человеке. Для ее
решения может быть поставлен достаточно трудоемкий эксперимент. Пока же он не
поставлен, целесообразно принимать порядковую шкалу, так как это гарантирует от
возможных ошибок.
- дело
специалиста соответствующей прикладной области. Так, оценки привлекательности
профессий мы считали измеренными в порядковой шкале. Однако отдельные социологи
не соглашались с этим, считая, что выпускники школ пользуются шкалой с более
узкой группой допустимых преобразований, например, интервальной шкалой.
Очевидно, эта проблема относится не к математике, а к наукам о человеке. Для ее
решения может быть поставлен достаточно трудоемкий эксперимент. Пока же он не
поставлен, целесообразно принимать порядковую шкалу, так как это гарантирует от
возможных ошибок.
Порядковые шкалы широко распространены не только в социально-экономических исследованиях. Они применяются в медицине - шкала стадий гипертонической болезни по Мясникову, шкала степеней сердечной недостаточности по Стражеско-Василенко-Лангу, шкала степени выраженности коронарной недостаточности по Фогельсону; в минералогии - шкала Мооса (тальк - 1, гипс - 2, кальций - 3, флюорит - 4, апатит - 5, ортоклаз - 6, кварц - 7, топаз - 8, корунд - 9, алмаз - 10), по которому минералы классифицируются согласно критерию твердости; в географии - бофортова шкала ветров ("штиль", "слабый ветер", "умеренный ветер" и др.) и т.д. Напомним, что по шкале интервалов измеряют величину потенциальной энергии или координату точки на прямой, на которой не отмечены ни начало, ни единица измерения; по шкале отношений - большинство физических единиц: массу тела, длину, заряд, а также цены в экономике. Время измеряется по шкале разностей, если год принимаем естественной единицей измерения, и по шкале интервалов в общем случае. В процессе развития соответствующей области знания тип шкалы может меняться. Так, сначала температура измерялась по порядковой шкале (холоднее - теплее), затем - по интервальной (шкалы Цельсия, Фаренгейта, Реомюра) и, наконец, после открытия абсолютного нуля температур - по шкале отношений (шкала Кельвина). Следует отметить, что среди специалистов иногда имеются разногласия по поводу того, по каким шкалам следует считать измеренными те или иные реальные величины.
Отметим, что термин "репрезентативная" использовался, чтобы отличить рассматриваемый подход к теории измерений от классической метрологии, а также от работ А.Н.Колмогорова и А. Лебега, связанных с измерением геометрических величин, от "алгоритмической теории измерения" и др.
Необходимость
использования в математических моделях реальных явлений таких объектов
нечисловой природы, как бинарные отношения, множества, нечеткие множества,
кратко была показана выше. Здесь же обратим внимание, что используемые в
классической статистике результаты наблюдений также "не совсем числа".
А именно, любая величина X измеряется всегда с некоторой
погрешностью ![]() и
результатом наблюдения является
и
результатом наблюдения является
![]()
Как уже отмечалось, погрешностями измерений занимается метрология. Отметим справедливость следующих фактов:
а)
для большинства реальных измерений невозможно полностью исключить
систематическую ошибку, т.е. ![]()
б)
распределение ![]() в подавляющем большинстве случаев не
является нормальным (см. главу 4);
в подавляющем большинстве случаев не
является нормальным (см. главу 4);
в)
измеряемую величину X и погрешность ее измерения ![]() обычно
нельзя считать независимыми случайными величинами;
обычно
нельзя считать независимыми случайными величинами;
г) распределение погрешностей оценивается по результатам специальных наблюдений, следовательно, полностью известным считать его нельзя; зачастую исследователь располагает лишь границами для систематической погрешности и оценками таких характеристик для случайной погрешности, как дисперсия или размах.
Приведенные
факты показывают ограниченность области применимости распространенной модели
погрешностей, в которой X и ![]() рассматриваются
как независимые случайные величины, причем
рассматриваются
как независимые случайные величины, причем ![]() имеет
нормальное распределение с нулевым математическим ожиданием.
имеет
нормальное распределение с нулевым математическим ожиданием.
Строго
говоря, результаты наблюдения всегда имеют дискретное распределение, поскольку
описываются числами с небольшими (1 - 5) числом значащих цифр. Возникает
дилемма: либо признать, что непрерывные распределения - фикция, и прекратить
ими пользоваться, либо считать, что непрерывные распределения имеют
"реальные" величины X,
которые мы наблюдаем с принципиально неустранимой погрешностью ![]() . Первый
выход в настоящее время нецелесообразен, так как потребует отказаться от
большей части разработанного математического аппарата. Из второго следует
необходимость изучения влияния неустранимых погрешностей на статистические
выводы.
. Первый
выход в настоящее время нецелесообразен, так как потребует отказаться от
большей части разработанного математического аппарата. Из второго следует
необходимость изучения влияния неустранимых погрешностей на статистические
выводы.
Погрешности
![]() можно
учитывать либо с помощью вероятностной модели (
можно
учитывать либо с помощью вероятностной модели (![]() -
случайная величина, имеющая функцию распределения, вообще говоря, зависящую от X), либо с помощью нечетких множеств. Во
втором случае приходим к теории нечетких чисел и к ее частному случаю -
статистике интервальных данных (см. главу 9).
-
случайная величина, имеющая функцию распределения, вообще говоря, зависящую от X), либо с помощью нечетких множеств. Во
втором случае приходим к теории нечетких чисел и к ее частному случаю -
статистике интервальных данных (см. главу 9).
Другой
источник появления погрешности ![]() связан
с принятой в конструкторской и технологической документации системой допусков
на контролируемые параметры изделий и деталей, с использованием шаблонов при
проверке контроля качества продукции. В этих случаях характеристики
связан
с принятой в конструкторской и технологической документации системой допусков
на контролируемые параметры изделий и деталей, с использованием шаблонов при
проверке контроля качества продукции. В этих случаях характеристики ![]() определяются
не свойствами средств измерения, а применяемой технологией проектирования и
производства. В терминах математической статистики сказанному соответствует
группировка данных, при которой мы знаем, какому из заданных интервалов
принадлежит наблюдение, но не знаем точного значения результата наблюдения.
Применение группировки может дать экономический эффект, поскольку зачастую
легче (в среднем) установить, к какому интервалу относится результат
наблюдения, чем точно измерить его.
определяются
не свойствами средств измерения, а применяемой технологией проектирования и
производства. В терминах математической статистики сказанному соответствует
группировка данных, при которой мы знаем, какому из заданных интервалов
принадлежит наблюдение, но не знаем точного значения результата наблюдения.
Применение группировки может дать экономический эффект, поскольку зачастую
легче (в среднем) установить, к какому интервалу относится результат
наблюдения, чем точно измерить его.
Объекты нечисловой природы как результат статистической обработки данных. Объекты нечисловой природы появляются не только на "входе" статистической процедуры, но и в процессе обработки данных, и на "выходе" в качестве итога статистического анализа.
Рассмотрим
простейшую прикладную постановку задачи регрессии (см. также главу 5). Исходные
данные имеют вид ![]() . Цель
состоит в том, чтобы с достаточной точностью описать y как
полином от x, т.е. модель имеет вид
. Цель
состоит в том, чтобы с достаточной точностью описать y как
полином от x, т.е. модель имеет вид
![]() (2)
(2)
где
m - неизвестная степень полинома; ![]() -
неизвестные коэффициенты многочлена;
-
неизвестные коэффициенты многочлена; ![]() , -
погрешности, которые для простоты примем независимыми и имеющими одно и то же
нормальное распределение. (Здесь наглядно проявляется одна из причин живучести
модель на основе нормального распределения. Такие модели, хотя и неадекватны
реальной ситуации, с математической точки зрения позволяет проникнуть глубже в
суть изучаемого явления. Поэтому они пригодны для первоначального анализа
ситуации, как и в рассматриваемом случае. Дальнейшие научные исследования
должны быть направлены на снятие нереалистического предположения нормальности и
перехода к непараметрическим моделям погрешности.) Распространенная процедура
такова: сначала пытаются применить модель (2) для линейной функции (m = 1), при неудаче (неадекватности
модели) переходят к многочлену второго порядка (m = 2), если снова неудача, то берут модель (2) с m= 3 и т.д. (адекватность модели проверяют
по F-критерию Фишера).
, -
погрешности, которые для простоты примем независимыми и имеющими одно и то же
нормальное распределение. (Здесь наглядно проявляется одна из причин живучести
модель на основе нормального распределения. Такие модели, хотя и неадекватны
реальной ситуации, с математической точки зрения позволяет проникнуть глубже в
суть изучаемого явления. Поэтому они пригодны для первоначального анализа
ситуации, как и в рассматриваемом случае. Дальнейшие научные исследования
должны быть направлены на снятие нереалистического предположения нормальности и
перехода к непараметрическим моделям погрешности.) Распространенная процедура
такова: сначала пытаются применить модель (2) для линейной функции (m = 1), при неудаче (неадекватности
модели) переходят к многочлену второго порядка (m = 2), если снова неудача, то берут модель (2) с m= 3 и т.д. (адекватность модели проверяют
по F-критерию Фишера).
Обсудим свойства этой процедуры в
терминах математической статистики. Если степень полинома задана (m = m0), то его коэффициенты оценивают методом
наименьших квадратов, свойства этих оценок хорошо известны (см., например,
главу 5 или монографию [10, гл.26]). Однако в описанной выше реальной
постановке m тоже является неизвестным параметром и
подлежит оценке. Таким образом, требуется оценить объект (m, a0, a1, a2, …, am), множество значений которого можно
описать как ![]() Это -
объект нечисловой природы, обычные методы оценивания для него неприменимы, так
как m - дискретный параметр. В рассматриваемой
постановке разработанные к настоящему времени методы оценивания степени
полинома носят в основном эвристический характер (см., например, гл. 12
монографии [11]). Свойства описанной выше распространенной процедуры
рассмотрены в главе 5; где показано, что m при этом оценивается
несостоятельно, и найдено предельное распределение оценки этого параметра,
оказавшееся геометрическим.
Это -
объект нечисловой природы, обычные методы оценивания для него неприменимы, так
как m - дискретный параметр. В рассматриваемой
постановке разработанные к настоящему времени методы оценивания степени
полинома носят в основном эвристический характер (см., например, гл. 12
монографии [11]). Свойства описанной выше распространенной процедуры
рассмотрены в главе 5; где показано, что m при этом оценивается
несостоятельно, и найдено предельное распределение оценки этого параметра,
оказавшееся геометрическим.
В
более общем случае линейной регрессии данные имеют вид ![]() где
где
![]() -
вектор предикторов (факторов, объясняющих переменных), а модель такова:
-
вектор предикторов (факторов, объясняющих переменных), а модель такова:
![]() (3)
(3)
(здесь
K - некоторое подмножество множества {1,2,…,n}; ![]() - те же, что и в модели (2); aj - неизвестные коэффициенты при
предикторах с номерами из K). Модель (2)
сводится к модели (3), если
- те же, что и в модели (2); aj - неизвестные коэффициенты при
предикторах с номерами из K). Модель (2)
сводится к модели (3), если
![]()
В модели (2) есть естественный порядок ввода предикторов в рассмотрение - в соответствии с возрастанием степени, а в модели (3) естественного порядка нет, поэтому здесь стоит произвольное подмножество множества предикторов. Есть только частичный порядок - чем мощность подмножества меньше, тем лучше. Модель (3) особенно актуальна в задачах управления качеством продукции и других технико-экономических исследованиях, в экономике, маркетинге и социологии, когда из большого числа факторов, предположительно влияющих на изучаемую переменную, надо отобрать по возможности наименьшее число значимых факторов и с их помощью сконструировать прогнозирующую формулу (3).
Задача оценивания модели (3) разбивается на две последовательные задачи: оценивание множества K - подмножества множества всех предикторов, а затем - неизвестных параметров aj. Методы решения второй задачи хорошо известны и подробно изучены. Гораздо хуже обстоит дело с оцениванием объекта нечисловой природы K. Как уже отмечалось, существующие методы - в основном эвристические, они зачастую не являются даже состоятельными. Даже само понятие состоятельности в данном случае требует специального определения. Пусть K0 - истинное подмножество предикторов, т.е. подмножество, для которого справедлива модель (3), а подмножество предикторов Kn - его оценка. Оценка Kn называется состоятельной, если
![]()
где
![]() -
символ симметрической разности множеств; Card(K) означает число элементов в множестве K, а предел понимается в смысле сходимости
по вероятности.
-
символ симметрической разности множеств; Card(K) означает число элементов в множестве K, а предел понимается в смысле сходимости
по вероятности.
Задача оценивания в моделях регрессии, таким образом, разбивается на две - оценивание структуры модели и оценивание параметров при заданной структуре. В модели (2) структура описывается неотрицательным целым числом m, в модели (3) - множеством K. Структура - объект нечисловой природы. Задача ее оценивания сложна, в то время как задача оценивания численных параметров при заданной структуре хорошо изучена, разработаны эффективные (в смысле математической статистики) методы.
Такова же ситуация и в других методах многомерного статистического анализа - в факторном анализе (включая метод главных компонент) и в многомерном шкалировании. Ряд иных примеров можно найти в списке оптимизационных постановок основных проблем прикладного многомерного статистического анализа, приведенном в монографии [12].
Перейдем к объектам нечисловой природы на "выходе" статистической процедуры. Примеры многочисленны. Разбиения - итог работы многих алгоритмов классификации, в частности, алгоритмов кластер-анализа. Ранжировки - результат упорядочения профессий по привлекательности или автоматизированной обработки мнений экспертов - членов комиссии по подведению итогов конкурса научных работ. (В последнем случае используются ранжировки со связями; так, в одну группу, наиболее многочисленную, попадают работы, не получившие наград.) Из всех объектов нечисловой природы, видимо, наиболее часты на "выходе" дихотомические данные - принять или не принять гипотезу, в частности, принять или забраковать партию продукции. Результатом статистической обработка данных может быть множество, например зона наибольшего поражения при аварии, или последовательность множеств, например, "среднемерное" описание распространения пожара (см. главу 4 в монографии [3]). Нечетким множеством Э. Борель [13] еще в начале ХХ в. предлагал описывать представление людей о числе зерен, образующем "кучу". С помощью нечетких множеств формализуются значения лингвистических переменных, выступающих как итоговая оценка качества систем автоматизированного проектирования, сельскохозяйственных машин, бытовых газовых плит, надежности программного обеспечения или систем управления. Можно констатировать, что все виды объектов нечисловой природы могут появляться " на выходе" статистического исследования.
8.2. Вероятностные модели конкретных видов объектов нечисловой природы
В настоящем пункте рассмотрены основные вероятностные модели объектов нечисловой природы: дихотомических данных, результатов парных сравнений, бинарных отношений, рангов, объектов общей природы. Обсуждаются различные варианты вероятностных моделей, приведены краткие сведения об их практическом использовании (см. также обзор [14]).
Дихотомические данные. Рассмотрим базовую вероятностную модель дихотомических
данных - бернуллиевский вектор (в терминологии энциклопедии [15] - люсиан), т.е.
конечную последовательность ![]() независимых испытаний Бернулли
независимых испытаний Бернулли ![]() , для которых
, для которых ![]() и
и![]()
![]()
![]() причем вероятности pi могут
быть различны.
причем вероятности pi могут
быть различны.
Бернуллиевские
вектора часто применяются при практическом использовании эконометрических методов.
Так, они использованы в монографии [3] для описания равномерно распределенных случайных
толерантностей. Как известно, толерантность на множестве из m элементов можно
задать симметричной матрицей ||![]() || из 0 и 1, на главной диагонали которой стоят
1. Тогда случайная толерантность описывается распределением m(m-1)/2 дихотомических
случайных величин
|| из 0 и 1, на главной диагонали которой стоят
1. Тогда случайная толерантность описывается распределением m(m-1)/2 дихотомических
случайных величин ![]()
![]() а для равномерно распределенной (на множестве всех
толерантностей) толерантности эти случайные величины, как можно доказать, оказываются
независимыми и принимают значения 0 и 1 с равными вероятностями 1/2. Записав элементы
а для равномерно распределенной (на множестве всех
толерантностей) толерантности эти случайные величины, как можно доказать, оказываются
независимыми и принимают значения 0 и 1 с равными вероятностями 1/2. Записав элементы
![]() задающей такую толерантность матрицы в строку, получим
бернуллиевский вектор с k=m(m-1)/2 и pi = 1/2,
задающей такую толерантность матрицы в строку, получим
бернуллиевский вектор с k=m(m-1)/2 и pi = 1/2, ![]()
В
связи с оцениванием по статистическим данным функции принадлежности нечеткой толерантности
в 1970-е годы была построена теория случайных толерантностей с такими независимыми
![]() что вероятности
что вероятности ![]() произвольны (см. об этом монографию [3]).
произвольны (см. об этом монографию [3]).
Случайные множества с независимыми элементами использовались как общий язык для описания парных сравнений и случайных толерантностей. В статьях [16] и [17] термин "люсиан" применялся как сокращение для выражения "случайные множества с независимыми элементами". В работе [18], являющейся продолжением [17] и содержащей описание расчетных методов, вытекающих из результатов [17], этот термин не употреблялся вообще, хотя указанный объект (т.е. бернуллиевский вектор) был основным предметом изучения. Это объясняется тем, что изложение в работе [18] шло на языке обработки результатов парных сравнений, которые для прикладника никак не связаны с множествами.
В дальнейшем был выявлен ещё ряд областей, в которых может оказаться полезным разработанный математический аппарат решения различных эконометрических задач, связанных с бернуллиевскими векторами. Перечислим эти области, включая ранее названные: анализ случайных толерантностей; случайные множества с независимыми элементами; обработка результатов независимых парных сравнений; статистические методы анализа точности и стабильности технологического процесса, а также анализ и синтез планов статистического приемочного контроля (по альтернативным, т.е. дихотомическим, признакам); обработка маркетинговых и социологических анкет (с закрытыми вопросами типа "да"-"нет"); обработка социально-психологических и медицинских данных, в частности, ответов на психологические тесты типа MMPI (используемых в задачах управления персоналом), топографических карт (применяемых для анализа и прогноза зон поражения при технологических авариях, распространении коррозии, распространении экологически вредных загрязнений в других ситуациях) и т.д.
Теорию бернуллиевских векторов можно выразить в терминах любой из этих теоретических и прикладных областей. Однако терминология одной из этих областей "режет слух" и приводит к недоразумениям в другой из них. Поэтому мы считаем целесообразным использовать термины "бернуллиевский вектор" в указанном выше значении, не связанном ни с какой из перечисленных областей приложения этой теории (в ряде публикаций в том же значении использовался термин "люсиан").
Распределение
бернуллиевского вектора Х полностью описывается вектором ![]() ,т.е. нечетким подмножеством множества {1,2,...,k}.
Действительно, для любого детерминированного вектора
,т.е. нечетким подмножеством множества {1,2,...,k}.
Действительно, для любого детерминированного вектора ![]() из 0 и 1 имеем
из 0 и 1 имеем
![]()
где h(x,p)=p при х=1 и h(х,р)=1-р при х=0.
Теперь можно уточнить способы использования люсианов при эконометрическом моделировании. Бернуллиевскими векторами можно моделировать: результаты статистического контроля (0-годное изделие, 1-дефектное); результаты маркетинговых и социологических опросов (0-опрашиваемый выбрал первую из двух подсказок, 1-вторую); распределение посторонних включений в материале (0 - нет включения в определенном объеме материала, 1 - есть); результаты испытаний и анализов (0 - нет нарушений требований нормативно-технической документации, 1 - есть такие нарушения); процессы распространения, например, пожаров (0 - нет загорания, 1 - есть; подробнее см. [3, с.215-223]); технологические процессы (0 - процесс находится в границах допуска,1 - вышел из них); ответы экспертов (опрашиваемых) о сходстве объектов (проектов, образцов) и т.д.
Парные
сравнения. Общую модель парных сравнений
опишем согласно монографии Г. Дэвида [9, с.9]. Предположим, что t объектов
![]() сравниваются попарно каждым из n экспертов.
Всего возможных пар для сравнения имеется
сравниваются попарно каждым из n экспертов.
Всего возможных пар для сравнения имеется ![]() Эксперт с номером
Эксперт с номером ![]() делает
делает ![]() повторных сравнений для каждой из s возможностей.
Пусть
повторных сравнений для каждой из s возможностей.
Пусть ![]() i,j=1,2,...,t,
i,j=1,2,...,t, ![]()
![]() =1,2,...,n;
=1,2,...,n; ![]() =1,2,...,
=1,2,..., ![]() -случайная величина, принимающая значение 1 или 0
в зависимости от того, предпочитает ли эксперт
-случайная величина, принимающая значение 1 или 0
в зависимости от того, предпочитает ли эксперт ![]() объект Ai или объект
Aj в
объект Ai или объект
Aj в
![]() -м сравнении двух объектов. Предполагается, что все
сравнения проводятся независимо друг от друга, так что случайные величины
-м сравнении двух объектов. Предполагается, что все
сравнения проводятся независимо друг от друга, так что случайные величины ![]() независимы в совокупности, если не считать того,
что
независимы в совокупности, если не считать того,
что ![]()
![]() Положим
Положим
![]()
Ясно,
что описанная эконометрическая модель парных сравнений представляет собой частный
случай бернуллиевского вектора. В этой модели число наблюдений равно числу неизвестных
параметров, поэтому для получения статистических выводов необходимо положить априорные
условия на ![]() , например [9, c.9]:
, например [9, c.9]:
![]() (нет эффекта от повторений);
(нет эффекта от повторений);
![]() (нет эффекта от повторений и от экспертов).
(нет эффекта от повторений и от экспертов).
Теорию независимых парных сравнений целесообразно
разделить на две части - непараметрическую, в которой статистические задачи ставятся
непосредственно в терминах ![]() , и параметрическую, в которой вероятности
, и параметрическую, в которой вероятности ![]() выражаются через меньшее число иных параметров. Ряд
результатов непараметрической теории парных сравнений непосредственно вытекает из
теории бернуллиевских векторов.
выражаются через меньшее число иных параметров. Ряд
результатов непараметрической теории парных сравнений непосредственно вытекает из
теории бернуллиевских векторов.
В
параметрической теории парных сравнений наиболее популярна так называемая линейная
модель [9, c.11], в которой предполагается , что каждому объекту Ai можно сопоставить некоторую "ценность" Vi так,
что вероятность предпочтения ![]() (т.е. предполагается дополнительно, что эффект от
повторений и от экспертов отсутствует ) выражается следующим образом:
(т.е. предполагается дополнительно, что эффект от
повторений и от экспертов отсутствует ) выражается следующим образом:
![]() (1)
(1)
где H(x) - функция распределения, симметричная относительно 0, т.е.
![]() (2)
(2)
при всех x.
Широко применяются модели Терстоуна - Мостеллера и Брэдли - Терри , в которых H(х) - соответственно функции нормального и логистического распределений. Поскольку функция Ф(х) стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1 и функция
![]()
стандартного логистического распределения удовлетворяют (см., например, [19]) соотношению
![]()
то для обоснованного выбора по статистическим данным между моделями Терстоуна-Мостеллера и Брэдли-Терри необходимо не менее тысячи наблюдений (ср. п.4.2 выше).
Соотношение (1) вытекает из следующей модели поведения
эксперта: он измерят "ценность" Vi и Vj объектов Ai и
Aj, но с ошибками ![]() и
и ![]() соответственно, а затем сравнивает свои оценки ценности
объектов
соответственно, а затем сравнивает свои оценки ценности
объектов ![]() и
и ![]() Если
Если ![]() то он предпочитает Ai, в противном случае - Aj. Тогда
то он предпочитает Ai, в противном случае - Aj. Тогда
![]() (3)
(3)
Обычно
предполагают, что субъективные ошибки эксперта ![]() и
и ![]() независимы и имеют одно и то же непрерывное распределение.
Тогда функция распределения Н(х) из соотношения (3) непрерывна и удовлетворяет
функциональному уравнению (2).
независимы и имеют одно и то же непрерывное распределение.
Тогда функция распределения Н(х) из соотношения (3) непрерывна и удовлетворяет
функциональному уравнению (2).
Существует
много разновидностей моделей парных сравнений, постоянно предполагаются новые. В
качестве примера опишем модель парных сравнений, основанную не на процедуре упорядочения,
а на определении сходства объектов. Пусть каждому объекту Ai соответствует
точка ai в
r-мерном евклидовом пространстве Rr. Эксперт "измеряет" ai и aj с
ошибками ![]() и
и ![]() соответственно и в случае, если евклидово расстояние
между
соответственно и в случае, если евклидово расстояние
между ![]() и
и ![]() меньше 1, заявляет о сходстве объектов Ai и
Aj, в противном случае - об их различии. Предполагается, что ошибки
меньше 1, заявляет о сходстве объектов Ai и
Aj, в противном случае - об их различии. Предполагается, что ошибки ![]() и
и ![]() независимы и имеют одно и то же распределение, например,
круговое нормальное распределение с нулевым математическим ожиданием и дисперсией
координат
независимы и имеют одно и то же распределение, например,
круговое нормальное распределение с нулевым математическим ожиданием и дисперсией
координат ![]() . Целью статистической обработки является определение
по результатам парных сравнений оценок параметров a1, a2,…,ar, и
. Целью статистической обработки является определение
по результатам парных сравнений оценок параметров a1, a2,…,ar, и ![]() , а также
проверка согласия опытных данных с моделью.
, а также
проверка согласия опытных данных с моделью.
Рассмотренные модели парных сравнений могут быть обобщены в различных направлениях. Так, можно ввести понятие "ничья "- ситуации, когда эксперт оценивает объекты одинаково. Модели с учетом "ничьих" предполагают, что эксперт может отказаться от выбора одного из объектов и заявить об их эквивалентности, т. е. число возможных ответов увеличивается с 2 до 3. В моделях множественных сравнений эксперту представляется не два объекта , а три или большее число
Модели,
учитывающие "ничьи", строятся обычно с помощью используемых в психофизике
"порогов чувствительности": если ![]() (где r- порог чувствительности), то объекты
Ai и
Aj эксперт
объявляет неразличимыми. Приведем пример модели с "ничьими", основанной
на другом принципе. Пусть каждому объекту Ai соответствует
точка ai в
r-мерном линейном пространстве. Как и прежде , эксперт "измеряет
" объектные точки " ai
и aj с ошибками
(где r- порог чувствительности), то объекты
Ai и
Aj эксперт
объявляет неразличимыми. Приведем пример модели с "ничьими", основанной
на другом принципе. Пусть каждому объекту Ai соответствует
точка ai в
r-мерном линейном пространстве. Как и прежде , эксперт "измеряет
" объектные точки " ai
и aj с ошибками
![]() и
и ![]() соответственно, т.е. принимает решение на основе
yi =
соответственно, т.е. принимает решение на основе
yi = ![]() и yj =
и yj = ![]() . Если все координаты yi больше
соответствующих координат yj , то Ai предпочитается
Aj. Соответственно, если каждая координата yi меньше
координаты yj с тем
же номером , то эксперт считает наилучшим объект Aj. Во всех остальных случаях эксперт объявляет о ничейной ситуации. Эта
модель при r=1 переходит в описанную выше линейную модель. Она связана с
принципом Парето в теории группового выбора и предусматривает выбор оптимального
по Парето объекта, если он существует (роль согласуемых критериев играют процедуры
сравнения значений отдельных координат), и отказ от выбора, если такого объекта
нет.
. Если все координаты yi больше
соответствующих координат yj , то Ai предпочитается
Aj. Соответственно, если каждая координата yi меньше
координаты yj с тем
же номером , то эксперт считает наилучшим объект Aj. Во всех остальных случаях эксперт объявляет о ничейной ситуации. Эта
модель при r=1 переходит в описанную выше линейную модель. Она связана с
принципом Парето в теории группового выбора и предусматривает выбор оптимального
по Парето объекта, если он существует (роль согласуемых критериев играют процедуры
сравнения значений отдельных координат), и отказ от выбора, если такого объекта
нет.
Можно строить модели, учитывающие порядок предъявления объектов при сравнении, зависимость результата сравнения от результатов предшествующих сравнений. Опишем одну из подобных моделей.
Пусть эксперт сравнивает три объекта - A, B, C, причем сначала сравниваются A и B, потом - B и C и, наконец, A и C. Для определенности пусть A>B будет означать, что A более предпочтителен, чем B. Пусть при предъявлении двух объектов
![]()
Теперь пусть пара B, C предъявляется после пары A, B. Естественно предположить, что высокая оценка B в первом сравнении повышает вероятность предпочтения B и во втором, и, наоборот, отрицательное мнение о B в первом сравнении сохраняется и при проведении второго сравнения. Это предположение проще всего учесть в модели следующим образом:
![]()
где
![]() - некоторое положительное число, показывающее степень
влияния первого сравнения на второе. По аналогичным причинам вероятности исхода
третьего сравнения в зависимости от результатов первых двух можно описать так:
- некоторое положительное число, показывающее степень
влияния первого сравнения на второе. По аналогичным причинам вероятности исхода
третьего сравнения в зависимости от результатов первых двух можно описать так:
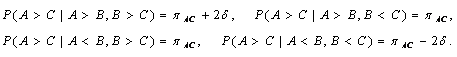
Статистическая задача состоит в определении параметров
![]()
![]()
![]() и
и ![]() по результатам сравнений, проведенных n экспертами,
и в проверке адекватности модели.
по результатам сравнений, проведенных n экспертами,
и в проверке адекватности модели.
Ясно, что можно рассматривать и другие модели, в частности, учитывающие тягу экспертов к транзитивности ответов. Очевидно, что проблемы построения моделей парных сравнений относятся не к эконометрической теории, а к тем прикладным областям, для решения задач которых развиваются методы парных сравнений, например, к экономике предприятия, стратегическому менеджменту, производственной психологии, изучению поведения потребителей, экспертным оценкам и т. д.
Метод парных сравнений был введен в 1860 г. Г. Т. Фехнером для решения задач психофизики. Расскажем об этом несколько подробнее. Как известно, основателем психофизики по праву считается Густав Теодор Фехнер (1801 - 1887), а год выхода в свет его фундаментальной работы "Элементы психофизики"(1860) - датой рождения новой науки; в этой работе широко применялся предложенный Г.Т. Фехнером метод парных сравнений (обсуждение событий тех лет с современных позиций дано в монографии [9, c.14-16]).
С точки зрения математической статистики приведенные выше модели не представляют большого теоретического интереса: оценки параметров находятся обычно методом максимального правдоподобия, а проверка согласия проводится по критерию отношения правдоподобия или асимптотически эквивалентными ему критериями типа хи-квадрат [9]. Вычислительные процедуры обычно сложны и плохо исследованы; их можно упростить и одновременно повысить обоснованность, перейдя от оценок максимального правдоподобия к одношаговым оценкам [20].
Отметим
некоторые сложности при обосновании возможности использовании линейных моделей типа
(1) - (3). Эконометрическая теория достаточно проста, когда предполагается , что
каждому отдельному сравнению двух объектов соответствуют свои собственные ошибки
экспертов, причем все ошибки независимы в совокупности. Однако это предположение
отнюдь не очевидно с содержательной точки зрения. В качестве примера рассмотрим
три объекта A, B и C, которые сравнивают попарно: A и B,
B и C, A и
C. В соответствии со сказанным, в рассмотрение вводят 6 ошибок одного и того
же эксперта: ![]() и
и ![]() в первом сравнении,
в первом сравнении, ![]() и
и ![]() -во втором,
-во втором, ![]() и
и ![]() - в третьем, причем все эти 6 случайных величин независимы
в совокупности. Между тем естественно думать, что мнения эксперта об одном и том
же объекте связаны между собой, т. е.
- в третьем, причем все эти 6 случайных величин независимы
в совокупности. Между тем естественно думать, что мнения эксперта об одном и том
же объекте связаны между собой, т. е. ![]() и
и ![]() зависимы, равно как
зависимы, равно как ![]() и
и ![]() , а также
, а также ![]() и
и ![]() . Более того, если принять, что точка зрения эксперта
полностью определена для него самого, то следует положить
. Более того, если принять, что точка зрения эксперта
полностью определена для него самого, то следует положить ![]() =
=![]() и соответственно
и соответственно ![]() =
=![]() и
и ![]() =
=![]() . При этом, напомним, случайные величины
. При этом, напомним, случайные величины![]() ,
, ![]() и др. интерпретируется как отклонения мнений отдельных
экспертов от истины. Видимо, ошибку эксперта целесообразно считать состоящей из
двух слагаемых, а именно: отклонения от истины, вызванного внутренними особенностями
эксперта (систематическая погрешность) и колебания мнения эксперта в связи с очередным
парным сравнением (случайная погрешность). Игнорирование систематической погрешности
облегчает развитие математико-статистической теории, а ее учет приводит к необходимости
изучения зависимых парных сравнений.
и др. интерпретируется как отклонения мнений отдельных
экспертов от истины. Видимо, ошибку эксперта целесообразно считать состоящей из
двух слагаемых, а именно: отклонения от истины, вызванного внутренними особенностями
эксперта (систематическая погрешность) и колебания мнения эксперта в связи с очередным
парным сравнением (случайная погрешность). Игнорирование систематической погрешности
облегчает развитие математико-статистической теории, а ее учет приводит к необходимости
изучения зависимых парных сравнений.
При обработке результатов парных сравнений первый этап - проверка согласованности. Понятие согласованности уточняется различными способами, но все они имеют один и тот же смысл проверки однородности обрабатываемого материала, т.е. того, что целесообразно агрегировать мнения отдельных экспертов, объединить данные и совместно их обрабатывать. При отсутствии однородности данные разбиваются на группы (классы, кластеры, таксоны) с целью обеспечения однородности внутри отдельных групп. Естественно, согласованность целесообразно проверять, вводя возможно меньше гипотез о структуре данных. Следовательно, целесообразно пользоваться для этого непараметрической теорией парных сравнений, основанной на теории бернуллиевских векторов.
Хорошо известно, что модели парных сравнений можно с успехом применять в экспертных и экспериментальных процедурах упорядочивания и выбора, в частности, для анализа голосований, турниров, выбора наилучшего объекта (проекта, образца, кандидатуры); в планировании и анализе сравнительных экспериментов и испытаний; в органолептической экспертизе (в частности, дегустации); при изучении поведения потребителей; визуальной колоритмии, определении индивидуальных рейтингов и вообще изучении предпочтений при выборе и т. д. (подробнее см. [3,9]).
Бинарные отношения. Теорию ранговой корреляции [6, 21] можно рассматривать как теорию статистического анализа случайных ранжировок, равномерно распределенных на множестве всех ранжировок. Так, при обработке данных классического психофизического эксперимента по упорядочению кубиков соответственно их весу, подробно описанного в работе [22], оказалась адекватной следующая т.н. Т-модель ранжирования.
Пусть
имеется t объектов ![]() причем каждому
объекту
причем каждому
объекту ![]() соответствует
число ai, описывающее его положение на шкале изучаемого признака.
Испытуемый упорядочивает объекты так, как если бы оценивал соответствующие им значения
с ошибками, т.е. находил
соответствует
число ai, описывающее его положение на шкале изучаемого признака.
Испытуемый упорядочивает объекты так, как если бы оценивал соответствующие им значения
с ошибками, т.е. находил ![]() i=1,2,…n, где
i=1,2,…n, где
![]() - ошибка
при рассмотрении i-го объекта, а затем располагал бы объекты в том порядке,
в каком располагаются
- ошибка
при рассмотрении i-го объекта, а затем располагал бы объекты в том порядке,
в каком располагаются ![]() В этом случае
вероятность появления упорядочения
В этом случае
вероятность появления упорядочения ![]() есть
есть ![]() а ранги
а ранги
![]() объектов
являются рангами случайных величин
объектов
являются рангами случайных величин ![]() , полученных
при их упорядочении в порядке возрастания. Кроме того, для простоты расчетов в модели
предполагается, что ошибки испытуемого
, полученных
при их упорядочении в порядке возрастания. Кроме того, для простоты расчетов в модели
предполагается, что ошибки испытуемого ![]() независимы
и имеют нормальное распределение с математическим ожиданием 0 и дисперсией
независимы
и имеют нормальное распределение с математическим ожиданием 0 и дисперсией ![]() . Как уже
отмечалось, бинарное отношение на множестве из t элементов полностью описывается
матрицей из 0 и 1 порядка
. Как уже
отмечалось, бинарное отношение на множестве из t элементов полностью описывается
матрицей из 0 и 1 порядка ![]() . Поэтому
задать распределение случайного бинарного отношения - это то же самое, что задать
распределение вероятностей на множестве всех матриц описанного вида, состоящем из
. Поэтому
задать распределение случайного бинарного отношения - это то же самое, что задать
распределение вероятностей на множестве всех матриц описанного вида, состоящем из
![]() элементов.
Пространства ранжировок, разбиений, толерантностей зачастую удобно считать подпространствами
пространства всех бинарных отношений, тогда распределения вероятностей на них -
частные случаи описанного выше распределения, выделенные тем, что вероятности принадлежности
соответствующим подпространствам равны 1. Распределение произвольного бинарного
отношения описывается
элементов.
Пространства ранжировок, разбиений, толерантностей зачастую удобно считать подпространствами
пространства всех бинарных отношений, тогда распределения вероятностей на них -
частные случаи описанного выше распределения, выделенные тем, что вероятности принадлежности
соответствующим подпространствам равны 1. Распределение произвольного бинарного
отношения описывается ![]() -1 параметрами,
распределение случайной ранжировки (без связей) - (t!-1) параметрами, а описанная
выше T-модель ранжирования - (t+1) параметром. При t=4 эти
числа равны соответственно 65535, 23 и 5. Первое из этих чисел показывает практическую
невозможность использования в эконометрических моделях произвольных бинарных отношений,
поскольку по имеющимся данным невозможно оценить столь большое число параметров.
Приходится ограничиваться теми или иными семействами бинарных отношений - ранжировками,
разбиениями, толерантностями и др. Модель произвольной случайной ранжировки при
t=5 описывается 119 параметрами, при t=6 - уже 719 параметрами, при
t=7 число параметром достигает 5049, что уже явно за возможностями оценивания.
В то же время T-модель ранжирования при t=7 описывается всего 8-ю
параметрами, а потому она практически пригодна.
-1 параметрами,
распределение случайной ранжировки (без связей) - (t!-1) параметрами, а описанная
выше T-модель ранжирования - (t+1) параметром. При t=4 эти
числа равны соответственно 65535, 23 и 5. Первое из этих чисел показывает практическую
невозможность использования в эконометрических моделях произвольных бинарных отношений,
поскольку по имеющимся данным невозможно оценить столь большое число параметров.
Приходится ограничиваться теми или иными семействами бинарных отношений - ранжировками,
разбиениями, толерантностями и др. Модель произвольной случайной ранжировки при
t=5 описывается 119 параметрами, при t=6 - уже 719 параметрами, при
t=7 число параметром достигает 5049, что уже явно за возможностями оценивания.
В то же время T-модель ранжирования при t=7 описывается всего 8-ю
параметрами, а потому она практически пригодна.
Что
естественно предположить относительно распределения случайного элемента со значениями
в том или ином пространстве бинарных отношений? Зачастую целесообразно считать,
что распределение имеет некий центр, попадание в который наиболее вероятно, а по
мере удаления от центра вероятности убывают. Это соответствует естественной модели
измерения с ошибкой; в классическом одномерном случае результат подобного измерения
описывается унимодальной симметричной плотностью, монотонно возрастающей слева от
модального значения, в котором плотность максимальна, и монотонно убывающей справа
от него. Чтобы ввести понятие монотонного распределения в пространстве бинарных
отношений, будем исходить из метрики в этом пространстве. Воспользовавшись тем,
что бинарные отношения C и D однозначно описываются матрицами ![]() и
и ![]() порядка
порядка
![]() соответственно,
рассмотрим расстояние (в несколько другой терминологии - метрику) в пространстве
бинарных отношений
соответственно,
рассмотрим расстояние (в несколько другой терминологии - метрику) в пространстве
бинарных отношений
![]() (4)
(4)
Метрика (4) в различных пространствах бинарных отношений - ранжировок, разбиений, толерантностей - может быть введена с помощью соответствующих систем аксиом. В работах [3, 23] дан обзор аксиоматическим подходам к получению метрики (4) в различных пространствах объектов нечисловой природы. В настоящее время метрику (4) обычно называют расстоянием Кемени в честь американского исследователя Джона Кемени, впервые получившего эту метрику исходя из предложенной им системы аксиом для расстояния между упорядочениями (ранжировками). Этой тематике посвящена первая глава учебника [24], на английском языке выпущенном под названием "Математические методы в социальных науках".
В статистике нечисловых данных используются и иные метрики, отличающиеся от расстояния Кемени. Более того, для использования понятия монотонного распределения, о котором сейчас идет речь, нет необходимости требовать выполнения неравенства треугольника, а достаточно, чтобы d(C,D) можно было рассматривать как показатель различия. Под показателем различия понимаем такую функцию d(C,D) двух бинарных отношений C и D, что d(C,D)=0 при C=D и увеличение d(C,D) интерпретируется как возрастание различия между C и D.
Определение 1. Распределение бинарного отношения X называется монотонным относительно расстояния (показателя различия) d с центром в C0, если из d(C,C0)<d(D,C0) следует, что P(X=C)>P(X=D)
Это определение впервые введено в монографии [3, c.196]. Оно может использоваться в любых пространствах бинарных отношений и, более того, в любых пространствах из конечного числа элементов, лишь бы в них была введена функция d(C,D) - показатель различия элементов С и D этого пространства. Монотонное распределение унимодально, мода находится в С0.
Определение
2. Распределение бинарного отношения X называется симметричным относительно
расстояния d с
центром в C0, если существует такая функция ![]() что
что
![]() (5)
(5)
Если распределение X монотонно и таково, что из d(C,C0) = d(D,C0) следует P(X=C) = P(X=D), то оно симметрично. Если функция f в формуле (5) монотонно строго убывает, то соответствующее распределение монотонно в смысле определения 1.
Поскольку толерантность на множестве из t элементов
задается 0,5t(t-1) элементами матрицы из 0 и 1 порядка ![]() , лежащими
выше главной диагонали, то распределение на множестве толерантностей задается в
общем случае
, лежащими
выше главной диагонали, то распределение на множестве толерантностей задается в
общем случае ![]() параметрами.
Естественно выделить семейство распределений, соответствующее независимым элементам
матрицы. Оно задается бернуллиевским вектором (люсианом) с 0,5t(t-1) параметрами
( выше бернуллиевские вектора рассмотрены подробнее). Математическая техника, необходимая
для изучения толерантностей с независимыми элементами, существенно проще, чем в
случае ранжировок и разбиений. Здесь легко отказаться от условия равномерности распределения.
Этому условию соответствует pij = 1/2, в то время как статистические методы анализа
люсианов, развитые в статистике нечисловых данных (см., например, работы [3,17,
18]) не налагают никаких существенных ограничений на pij .
параметрами.
Естественно выделить семейство распределений, соответствующее независимым элементам
матрицы. Оно задается бернуллиевским вектором (люсианом) с 0,5t(t-1) параметрами
( выше бернуллиевские вектора рассмотрены подробнее). Математическая техника, необходимая
для изучения толерантностей с независимыми элементами, существенно проще, чем в
случае ранжировок и разбиений. Здесь легко отказаться от условия равномерности распределения.
Этому условию соответствует pij = 1/2, в то время как статистические методы анализа
люсианов, развитые в статистике нечисловых данных (см., например, работы [3,17,
18]) не налагают никаких существенных ограничений на pij .
Как уже отмечалось, при обработке мнений экспертов сначала проверяют согласованность. В частности, если мнения экспертов описываются монотонными распределениями, то для согласованности необходимо совпадение центров этих распределений. К сожалению, рассмотренные выше классические методы проверки согласованности для ранжировок, основанные на коэффициентах ранговой корреляции и конкордации, позволяют лишь отвергнуть гипотезу о равнораспределенности, но не установить, можно ли считать, что центры соответствующих экспертам распределений совпадают или же, например, существует две группы экспертов, каждая со своим центром. Теория случайных толерантностей лишена этого недостатка. Отсюда вытекают следующие практические рекомендации.
Пусть цель обработки экспертных данных состоит в получении ранжировки, отражающей групповое мнение. Однако согласно рекомендуемой процедуре экспертного опроса пусть эксперты не упорядочивают объекты, а проводят парные сравнения, сравнивая каждый из рассматриваемых объектов со всеми остальными, причем ровно один раз. Когда ответ эксперта - толерантность, но, вообще говоря, не ранжировка, поскольку в ответах эксперта может нарушаться транзитивность.
Возможны два пути обработки данных. Первый - превратить ответ эксперта в ранжировку (тем или иным способом "спроектировав" на пространство ранжировок), а затем проверять согласованность ранжировок с помощью известных критериев. При этом от толерантности перейти к ранжировке можно, например, так. Будем выбирать ближайшую (в смысле применяемого расстояния) матрицу к матрице ответов эксперта из всех, соответствующих ранжировкам без связей.
Второй путь - проверить согласованность случайных толерантностей, а групповое мнение искать с помощью медианы Кемени (см. ниже) непосредственно по исходным данным, т.е. по толерантностям. Групповое мнение при этом может быть найдено в пространстве ранжировок. Второй путь мы считаем более предпочтительным, поскольку при этом обеспечивается более адекватная проверка согласованности и исключается процедура укладывания мнения эксперта в "прокрустово ложе "ранжировки" (эта процедура может приводить как к потере информации, так и к принципиально неверным выводам).
Области применения статистики бинарных отношений многообразны: ранговая корреляция - оценка величины связи между переменными, измеренными в порядковой шкале; анализ экспертных или экспериментальных упорядочений; анализ разбиений технико-экономических показателей на группы сходных между собой; обработка данных о сходстве (взаимозаменяемости); статистический анализ классификаций; математические вопросы теории менеджмента и др.
Случайные множества. Будем рассматривать случайные подмножества некоторого
множества Q. Если Q состоит из конечного числа
элементов, то считаем, что случайное подмножество S
- это случайный элемент со значениями в 2Q - множестве
всех подмножеств множества Q, состоящем из 2card(Q) элементов. Чтобы
удовлетворить математиков, считаем, что все подмножества Q измеримы.
Тогда распределение случайного подмножества ![]() множества
Q - это
множества
Q - это
![]() (6)
(6)
В
формуле (6) предполагается, что ![]() где
где ![]() - вероятностное
пространство (здесь
- вероятностное
пространство (здесь ![]() - пространство элементарных событий, F-
- пространство элементарных событий, F-![]() -алгебра
случайных событий,
-алгебра
случайных событий, ![]() -вероятностная
мера на F), на котором определен случайный элемент
-вероятностная
мера на F), на котором определен случайный элемент ![]() .Через распределение
PS(A) выражаются вероятности различных событий, связанных
с S. Так ,чтобы найти вероятность накрытия фиксированного
элемента q случайным
множеством S, достаточно вычислить
.Через распределение
PS(A) выражаются вероятности различных событий, связанных
с S. Так ,чтобы найти вероятность накрытия фиксированного
элемента q случайным
множеством S, достаточно вычислить
![]()
где суммирование идет по всем подмножествам A множества Q, содержащим q. Пусть Q={q1, q2,…,qk}. Рассмотрим случайные величины, определяемые по случайному множеству S следующим образом
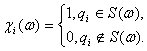
Определение
3. Случайное множество S называется
случайным множеством с независимыми элементами, если случайные величины ![]() независимы
(в совокупности).
независимы
(в совокупности).
Последовательность
случайных величин ![]() --бернуллиевский
вектор с
--бернуллиевский
вектор с ![]() и
и ![]() Из последней
формулы подпункта "Дихотомические данные" следует, что распределение случайного
множества с независимыми элементами задается формулой
Из последней
формулы подпункта "Дихотомические данные" следует, что распределение случайного
множества с независимыми элементами задается формулой
![]()
т.е. такие распределения образуют k = card(Q) - мерное параметрическое семейство, входящее в (2card(Q) - 1) - одномерное семейство всех распределений случайных подмножеств множества Q.
При исследовании случайных подмножеств произвольного множества Q будем рассматривать их как случайные величины со значениями в некотором пространстве подмножеств множества Q, например, в пространстве замкнутых подмножеств 2Q множества Q. Представляющими интерес лишь для математиков способами введения измеримой структуры в 2Q интересоваться не будем. Отсутствие специального интереса к проблеме измеримости связано с тем, что при эконометрическом моделировании и обработке на ЭВМ все случайные подмножества рассматриваются как конечные (т.е. подмножества конечного множества).
Случайные множества находят разнообразные применения в многообразных проблемах эконометрики и математической экономики, в том числе в задачах управлении запасами и ресурсами (см. об этом главу 5 в монографии [3]), в задачах менеджмента и маркетинга, в экспертных оценках, в частности, при анализе мнений голосующих или опрашиваемых, каждый из которых отмечает несколько пунктов из списка и т.д. Кроме того, случайные множества применяются в гранулометрии, при изучении пористых сред и объектов сложной природы в таких областях, как металлография, петрография, биология, в частности, математическая морфология, в изучении структуры веществ и материалов, в исследовании процессов распространения, в частности, просачивания, распространения пожаров, экологических загрязнений, при районировании, в том числе в изучении областей поражения, в частности, поражения металла коррозией и сердечной мышцы при инфаркте миокарда, и т.д., и т.п. Можно вспомнить о компьютерной томографии, о наглядном представлении сложной информации на экране компьютера, об изучении распространения рекламной информации, о картах Кохонена (популярный метод представления информации при применении нейросетей) и т.д.
Ранговые методы. Ранее установлено, что любой адекватный алгоритм в порядковой шкале является функцией от некоторой матрицы C. Пусть никакие два из результатов наблюдений x1, x2,…,xn не совпадают, а r1, r2,…,rn - их ранги. Тогда элементы матрицы C и ранги результатов наблюдений связаны взаимно однозначным соответствием:
![]()
а cij через ранги выражаются так: cij=1, если ri<rj , и cij=0 в противном случае.
Cказанное означает, что при обработке данных, измеренных в порядковой шкале, могут применяться только ранговые статистические методы. Отметим, что часто используемое в непараметрической статистике преобразование Y=F(x) (здесь F(x) - непрерывная функция распределения случайной величины X, причем F предполагается произвольной) фактически означает переход к порядковой шкале, поскольку статистические выводы при этом инвариантны относительно допустимых преобразований в порядковой шкале.
Разумеется, ранговые статистические методы могут применяться не только при обработке данных, измеренных в порядковой шкале. Так, для проверки независимости двух количественных признаков в случае, когда нет уверенности в нормальности соответствующего двумерного распределения, целесообразно пользоваться коэффициентами ранговой корреляции Кендалла или Спирмена.
Как было подробно обосновано в главах 4 и 5, в настоящее время с помощью непараметрических и прежде всего ранговых методов можно решать все те задачи эконометрики и прикладной статистики, что и с помощью параметрических методов, в частности, основанных на предположении нормальности. Однако параметрические методы вошли в массовое сознание исследователей и инженеров и мешают широкому внедрению более обоснованной и прогрессивной ранговой статистики. Так, при проверке однородности двух выборок вместо критерия Стъюдента целесообразно использовать ранговые методы, но пока это делается редко.
Объекты общей природы. Вероятностная модель объекта нечисловой природы в общем случае- случайный элемент со значениями в пространстве произвольного вида, а модель выборки таких объектов - совокупность независимых одинаково распределенных случайных элементов. Именно такая модель была использована для обработки наблюдений, каждое из которых - нечеткое множество [10].
Из-за имеющего разнобоя в терминологии приведем математические определения из справочника по теории вероятностей академика РАН Ю.В Прохорова и проф. Ю.А. Розанова [25].
Пусть
![]() -некоторое измеримое пространство;
-некоторое измеримое пространство; ![]() -измеримая функция
-измеримая функция ![]() на пространстве элементарных событий
на пространстве элементарных событий ![]() (где
(где ![]() - вероятностная мера на
- вероятностная мера на ![]() -алгебре F
- измеримых подмножеств
-алгебре F
- измеримых подмножеств ![]() , называемых событиями) со значениями в
, называемых событиями) со значениями в ![]() называется случайной величиной (чаще этот математический
объект называют случайным элементом, оставляя термин "случайная величина"
за частным случаем, когда Х - числовая прямая) в фазовом пространстве
называется случайной величиной (чаще этот математический
объект называют случайным элементом, оставляя термин "случайная величина"
за частным случаем, когда Х - числовая прямая) в фазовом пространстве ![]() . Распределением вероятностей этой случайной величины
. Распределением вероятностей этой случайной величины
![]() называется функция
называется функция ![]() на
на ![]() -алгебре
-алгебре ![]() фазового пространства, определенная как
фазового пространства, определенная как
![]() (7)
(7)
(распределение
вероятностей ![]() представляет собой вероятностную меру в фазовом пространстве
представляет собой вероятностную меру в фазовом пространстве
![]() ) [25, с. 132].
) [25, с. 132].
Пусть
![]() - случайные величины на пространстве случайных событий
- случайные величины на пространстве случайных событий
![]() в соответствующих фазовых пространствах
в соответствующих фазовых пространствах ![]() . Совместным распределением вероятностей этих величин
называется функция
. Совместным распределением вероятностей этих величин
называется функция ![]() , определенная на множествах
, определенная на множествах ![]()
![]()
![]() …,
…,![]() как
как
![]() (8)
(8)
Распределение
вероятностей ![]() как функция на полукольце множеств вида
как функция на полукольце множеств вида ![]()
![]() в произведении пространств
в произведении пространств ![]() представляет собой функцию распределения. Случайные
величины
представляет собой функцию распределения. Случайные
величины ![]() называются независимыми, если при любых B1, B2,…,Bn (см. [25,
с.133])
называются независимыми, если при любых B1, B2,…,Bn (см. [25,
с.133])
![]() . (9)
. (9)
Предположим,
что совместное распределение вероятностей ![]() случайных величин
случайных величин ![]() и
и ![]() абсолютно непрерывно относительно некоторой меры
Q на
произведении пространств
абсолютно непрерывно относительно некоторой меры
Q на
произведении пространств ![]() , являющейся произведением мер
, являющейся произведением мер ![]() и
и ![]() , т.е.:
, т.е.:
![]() (10)
(10)
для
любых ![]() и
и ![]() , где p(x,y)
- соответствующая плотность распределения вероятностей [25, с.145].
, где p(x,y)
- соответствующая плотность распределения вероятностей [25, с.145].
В
формуле (10) предполагается, что ![]() и
и ![]() - случайные величины на одном и том же пространстве
элементарных событий
- случайные величины на одном и том же пространстве
элементарных событий ![]() со значениями в фазовых пространствах
со значениями в фазовых пространствах ![]() и
и ![]() . Существование плотности p(x,y) вытекает из абсолютной непрерывности
. Существование плотности p(x,y) вытекает из абсолютной непрерывности ![]() относительно Q в соответствии с теоремой
Радона - Никодима.
относительно Q в соответствии с теоремой
Радона - Никодима.
Условное
распределение вероятностей ![]() может быть выбрано одинаковым для всех
может быть выбрано одинаковым для всех ![]() при которых случайная величина
при которых случайная величина ![]() сохраняет одно и то же значение:
сохраняет одно и то же значение: ![]() При почти каждом
При почти каждом ![]() (относительно распределения
(относительно распределения ![]() в фазовом пространстве
в фазовом пространстве ![]() ) условное распределение вероятностей
) условное распределение вероятностей ![]() где
где ![]() и
и ![]() будет абсолютно непрерывно относительно меры
будет абсолютно непрерывно относительно меры ![]() :
:
![]()
Причем соответствующая плотность условного распределения вероятностей будет иметь вид (см. [25, с.145-146]):
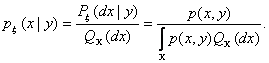 (11)
(11)
При построении вероятностных моделей реальных явлений важны вероятностные пространства из конечного числа элементарных событий. Для них перечисленные выше общие понятия становятся более прозрачными, в частности, снимаются вопросы измеримости (все подмножества конечного множества обычно считаются измеримыми). Вместо плотностей и условных плотностей рассматриваются вероятности и условные вероятности. Отметим, что вероятности можно рассматривать как плотности относительно меры, приписывающей каждому элементу пространства элементарных событий вес 1, т.е. считающей меры
![]()
(мера каждого множества равна числу его элементов). В целом ясно, что определения основных понятий теории вероятностей в общем случае практически не отличаются от таковых в элементарных курсах, во всяком случае с идейной точки зрения.
За последние двадцать лет в эконометрике и прикладной математической статистике сформировалась новая область - статистика нечисловых данных, она же - статистика объектов нечисловой природы. К настоящему времени она развита не менее, чем ранее выделенные статистика случайных величин, многомерный статистический анализ, статистика временных рядов и случайных процессов. Краткая сводка основных постановок и результатов математической статистики в пространствах нечисловой природы даны ниже в настоящей главе. Теория, построенная для результатов наблюдений, лежащих в пространствах общей природы, является центральным стержнем в статистике нечисловой природы. В ее рамках удалось разработать и изучить методы оценивания параметров и характеристик, проверки гипотез (в частности, с помощью статистик интегрального типа), параметрической и непараметрической регрессии (восстановления зависимостей), непараметрического оценивания плотности, дискриминантного и кластерного анализов и т.д.
Вероятностно-статистические методы, развитые для результатов наблюдений из пространств произвольного вида, позволяют единообразно проводить анализ данных из любого конкретного пространства. Так, в монографии [3] они применены к конечным случайным множествам, в работе [10] - к нечетким множествам. С их помощью установлено поведение обобщенного мнения экспертной комиссии (медианы Кемени) при увеличении числа экспертов, когда ответы экспертов лежат в том или ином пространстве бинарных отношений (см. см. пункт 4 настоящей главы и главу 12 ниже). В пункте 5 настоящей главы методы распознавания образов, основанные на непараметрических оценках плотности распределения вероятностей в пространстве общей природы, применены для разработки алгоритма диагностики в пространстве разнотипных данных (часть координат вектора измерена по количественным шкалам, часть - по качественным - см. главу 3).
8.3. Структура статистики объектов нечисловой природы
Как уже отмечалось, термин "статистика объектов нечисловой природы" впервые появился в 1979 г. в монографии [3]. В том же году в статье [16] была сформулирована программа развития этого нового направления прикладной математической статистики, которая к 1985 г. в основном была реализована.
Статистика объектов нечисловой природы как самостоятельное научное направление была выделена в нашей стране. Со второй половины 80-х годов существенно возрос интерес к этой тематике и у зарубежных исследователей. Это нашло отражение, в частности, на Первом Всемирном Конгрессе Общества математической статистики и теории вероятностей им. Бернулли, состоявшемся в сентябре 1986 г. в Ташкенте. Статистика объектов нечисловой природы используется в нормативно-технической и методической документации, ее применение позволяет получить существенный технико-экономический эффект (см. например, сводку [26]).
Однако тематика статистики объектов нечисловой природы обсуждалась до сих пор в основном в кругу развивающих ее специалистов, в результате она недостаточно отражена в монографической литературе. Цель настоящего пункта - дать введение в статистику объектов нечисловой природы, выделить ее структуру, указать основные идеи и результаты.
Напомним, что объектами нечисловой природы (см. также предыдущие пункты настоящей главы) называют элементы пространств, не являющихся линейными. Примерами являются бинарные отношения (ранжировки, разбиения, толерантности), множества, последовательности символов (тексты). Объекты нечисловой природы нельзя складывать и умножать на числа, не теряя при этом содержательного смысла. Этим они отличаются от издавна используемых в прикладной статистике (в качестве элементов выборок) чисел, векторов и функций.
Прикладную статистику по виду статистических данных принято делить на следующие направления:
статистика случайных величин (одномерная статистика);
многомерный статистический анализ;
статистика временных рядов и случайных процессов;
статистика объектов нечисловой природы.
При создании теории вероятностей и математической статистики исторически первыми были рассмотрены объекты нечисловой природы - белые и черные шары в урне. На основе соответствующих вероятностных моделей были введены биномиальное, гипергеометрическое и другие распределения, получены теоремы Муавра-Лапласа, Пуассона и др. Современное развитие этой тематики привело, в частности, к созданию теории статистического контроля качества продукции по альтернативному признаку (годен - не годен) в работах А.Н.Колмогорова, Б.В. Гнеденко, Ю.К. Беляева, Я.П. Лумельского и многих других (см., например, классические монографии [7,8]).
В семидесятых годах в связи с запросами практики весьма усилился интерес к статистическому анализу нечисловых данных. Московская группа, организованная Ю.Н. Тюриным и другими специалистами вокруг созданного в 1973 г. научного семинара "Экспертные оценки и нечисловая статистика", развивала в основном вероятностную статистику нечисловых данных. Были установлены разнообразные связи между различными видами объектов нечисловой природы и изучены свойства этих объектов. Московской группой выпущены десятки сборников и обзоров, перечень которых приведен в итоговой работе [4]. Хотя в названиях многих из этих изданий стоят слова "экспертные оценки", анализ содержания сборников показывает, что подавляющая часть статей посвящена математико-статистическим вопросам, а не проблемам проведения экспертиз. Частое употребление указанных слов отражает лишь один из импульсов, стимулирующих развитие статистики объектов нечисловой природы и идущих от запросов практики. При этом необходимо подчеркнуть, что полученные результаты могут и должны активно использоваться в теории и практике экспертных оценок.
Новосибирская группа (Г.С. Лбов, Б.Г. Миркин и др.), как правило, не использовала вероятностные модели, т.е. вела исследования в рамках анализа данных. В московской группе в рамках анализа данных также велись работы, в частности, Б.Г.Литваком. Исследования по статистике объектов нечисловой природы выполнялись также в Ленинграде, Ереване, Киеве, Таллине, Тарту, Красноярске, Минске, Днепропетровске, Владивостоке, Калинине и других научных центрах.
Внутреннее деление статистики объектов нечисловой природы. Внутри рассматриваемого направления эконометрики и прикладной статистики выделим следующие области.
1. Статистика конкретных видов объектов нечисловой природы.
2. Статистика в пространствах общей (произвольной) природы.
3. Применение идей, подходов и результатов статистики объектов нечисловой природы в классических областях прикладной статистики.
Единство рассматриваемому направлению придает прежде всего вторая составляющая, позволяющая с единой точки зрения подходить к статистическим задачам описания данных, оценивания, проверки гипотез при рассмотрении выборки, элементы которой имеют ту или иную конкретную природу. Внутри первой составляющей рассмотрим:
1.1) теорию измерений;
1.2) статистику бинарных отношений;
1.3) теорию люсианов (бернуллиевских векторов);
1.4) статистику случайных множеств;
1.5) статистику нечетких множеств;
1.6) многомерное шкалирование;
1.7) аксиоматическое введение метрик.
Перечисленные разделы тесно связаны друг с другом, как продемонстрировано, в частности, в работах [3,15] и первых двух пунктах настоящей главы. Вне данного перечня остались работы по хорошо развитым классическим областям - статистическому контролю, таблицам сопряженности, а также по анализу текстов и некоторые другие (см.[4]). Таким образом, рассмотрим постановки 1970-2000 гг. вероятностной статистики объектов нечисловой природы.
Статистика в пространствах общей природы. Пусть x1,x2,…,xn -элементы пространства X, не являющегося линейным.
Как определить среднее значение для x1,x2,…,xn? Поскольку нельзя складывать элементы X,
сравнивать их по величине, то необходимы подходы, принципиально новые по сравнению
с классическими. В статистике объектов нечисловой природы предложено использовать
показатель различия ![]() (содержательный смысл показателя различия: чем больше
d(x,y), тем больше различаются
x и
y) и определять среднее как решение экстремальной задачи
(содержательный смысл показателя различия: чем больше
d(x,y), тем больше различаются
x и
y) и определять среднее как решение экстремальной задачи
![]() (1)
(1)
Таким
образом, среднее En(d)- это совокупность всех тех ![]() , для которых функция
, для которых функция
![]() (2)
(2)
достигает минимума на X.
Для
классического случая X = R1 при
d(x,y) = (x-y)2 имеем En(d) =![]() , а при d(x,y)=|x-y| среднее En(d) совпадает с выборочной медианой (при нечетном объеме
выборки; а при четном - En(d) является отрезком с концами в двух средних элементах
вариационного ряда).
, а при d(x,y)=|x-y| среднее En(d) совпадает с выборочной медианой (при нечетном объеме
выборки; а при четном - En(d) является отрезком с концами в двух средних элементах
вариационного ряда).
Для ряда конкретных объектов среднее как решение экстремальной задачи вводилось рядом авторов. В 1929 г. итальянские статистики Джини и Гальвани применили такой подход для усреднения точек на плоскости и в пространстве Американский исследователь Джон Кемени решение задачи (1) называл медианой или средним для выборки, состоящей из ранжировок (см. монографию [24]). При моделировании лесных пожаров согласно выражению (1) было введено "среднеуклоняемое множество" для описания средней выгоревшей площади (см. об этом в монографии [3]). Общее определение среднего вида (1) было впервые введено в работе [16].
Основной результат, связанный со средними вида (1) - аналог закона больших чисел. Пусть x1,x2,…,xn - независимые одинаково распределенные случайные элементы со значениями в пространстве общей природы X. Теоретическим средним, или математическим ожиданием, в статистике объектов нечисловой природы называют
![]() . (3)
. (3)
Закон
больших чисел состоит в сходимости En(d) к En(x1,d) при ![]() . Поскольку и эмпирическое, и теоретическое средние
- множества, то понятие сходимости требует уточнения.
. Поскольку и эмпирическое, и теоретическое средние
- множества, то понятие сходимости требует уточнения.
Одно из возможных уточнений, впервые введенное в работе [16], таково. Для функции
![]() (4)
(4)
введем
понятие "![]() -пятки"
(
-пятки"
(![]() >0)
>0)
![]() (5)
(5)
Очевидно, ![]() - пятка f
- это окрестность Argmin(f) (если он достигается), заданная в терминах минимизируемой
функции. Тем самым снимается вопрос о выборе метрики в пространстве X.
Тогда при некоторых условиях регулярности для любого
- пятка f
- это окрестность Argmin(f) (если он достигается), заданная в терминах минимизируемой
функции. Тем самым снимается вопрос о выборе метрики в пространстве X.
Тогда при некоторых условиях регулярности для любого ![]() >0 вероятность события
>0 вероятность события
![]() (6)
(6)
стремится
к 1 при.![]() , т.е. справедлив
закон больших чисел. Подробное доказательство приводится в следующем пункте настоящей
главы.
, т.е. справедлив
закон больших чисел. Подробное доказательство приводится в следующем пункте настоящей
главы.
Естественное обобщение рассматриваемой задачи позволяет построить общую теорию оптимизационного подхода в статистике. Как известно, большинство задач прикладной статистики может быть представлено в качестве оптимизационных [12]. Как себя ведут решения экстремальных задач? Частные случаи этой постановки: как ведут себя при росте объема выборки оценки максимального правдоподобия, минимального контраста (в том числе робастные в смысле Тьюки-Хьюбера - см. главу 10), оценки нагрузок в факторном анализе и методе главных компонент при отсутствии нормальности, оценки метода наименьших модулей в регрессии и т.д.
Обычно
легко устанавливается, что для некоторых пространств X и последовательности
случайных функций.fn(x) при.![]() найдется
функция f(x) такая, что
найдется
функция f(x) такая, что
![]() (7)
(7)
для
любого ![]() (сходимость
по вероятности). Требуется вывести отсюда, что
(сходимость
по вероятности). Требуется вывести отсюда, что
![]() (8)
(8)
т.е.
решения экстремальных задач также сходятся. Понятие сходимости в соотношении
(8) уточняется с помощью ![]() -пяток, как
это сделано выше для закона больших чисел. Условия регулярности, при которых справедливо
предельное соотношение (8), приведены в исследовании [27]. В подавляющем большинстве
реальных задач эти условия выполняются.
-пяток, как
это сделано выше для закона больших чисел. Условия регулярности, при которых справедливо
предельное соотношение (8), приведены в исследовании [27]. В подавляющем большинстве
реальных задач эти условия выполняются.
Как
оценить распределение случайного элемента в пространстве общей природы? Поскольку
понятие функции распределения неприменимо, естественно использовать непараметрические
оценки плотности. Что такое плотность распределения вероятностей в пространстве
произвольной природы? Это функция ![]() такая, что
для любого измеримого множества (т.е. случайного события)
такая, что
для любого измеримого множества (т.е. случайного события) ![]() справедливо
соотношение
справедливо
соотношение
![]() , (9)
, (9)
где.![]() - некоторая
мера в X. Ряд непараметрических оценок плотности был предложен
в работе [16]. Например, аналогом ядерных оценок плотности является оценка
- некоторая
мера в X. Ряд непараметрических оценок плотности был предложен
в работе [16]. Например, аналогом ядерных оценок плотности является оценка
![]() (10)
(10)
где
d - показатель различия; H - ядерная функция; hn - последовательность
положительных чисел; ![]() - нормирующий
множитель. Удалось установить, что, что статистики типа (10) обладают такими же
свойствами, по крайней мере при фиксированном x,
что и их классические аналоги при X = R1. В частности, такой же скоростью сходимости. Некоторые
изменения необходимы при рассмотрении дискретных
- нормирующий
множитель. Удалось установить, что, что статистики типа (10) обладают такими же
свойствами, по крайней мере при фиксированном x,
что и их классические аналоги при X = R1. В частности, такой же скоростью сходимости. Некоторые
изменения необходимы при рассмотрении дискретных ![]() , каковыми являются многие пространства конкретных
объектов нечисловой природы. С помощью непараметрических оценок плотности можно
развивать регрессионный анализ, дискриминантный анализ и другие направления в пространствах
общей природы (см. пункт 5 ниже).
, каковыми являются многие пространства конкретных
объектов нечисловой природы. С помощью непараметрических оценок плотности можно
развивать регрессионный анализ, дискриминантный анализ и другие направления в пространствах
общей природы (см. пункт 5 ниже).
Для проверки гипотез согласия, однородности, независимости в пространствах общей природы могут быть использованы статистики интегрального типа
![]() (11)
(11)
где
![]() -последовательность
случайных функций на X;
-последовательность
случайных функций на X; ![]() - последовательность
случайных распределений (или зарядов). Обычно
- последовательность
случайных распределений (или зарядов). Обычно ![]() при
при ![]() сходится
по распределению к некоторой случайной функции
сходится
по распределению к некоторой случайной функции ![]() , а
, а ![]() - к распределению
F(x). Тогда распределение статистики интегрального типа
(11) сходится к распределению случайного элемента
- к распределению
F(x). Тогда распределение статистики интегрального типа
(11) сходится к распределению случайного элемента
![]() (12)
(12)
Условия, при которых это справедливо, даны в работе [28]. Пример применения - вывод предельного распределения статистики типа омега-квадрат для проверки симметрии распределения (см. главу 4).
Перейдем к статистике конкретных видов объектов нечисловой природы.
Теория измерений. Цель теории измерений - борьба с субъективизмом исследователя при приписывании численных значений реальным объектам. Так, расстояния можно измерять в метрах, микронах, милях, парсеках и других единицах измерения. Выбор единиц измерения зависит от исследователя, т.е. субъективен. Статистические выводы могут быть адекватны реальности только тогда, когда они не зависят от того, какую именно единицу измерения предпочтет исследователь, т.е. когда они инвариантны относительно допустимого преобразования шкалы.
Теория измерений известна в нашей стране уже около 30 лет. С начала семидесятых годов активно работают отечественные исследователи. В настоящее время изложение основ теории измерений включают в справочные издания, помещают в научно-популярные журналы и книги для детей. Однако она еще не стала общеизвестной среди специалистов, в частности, среди метрологов. Поэтому опишем одну из задач теории измерений (ср. главу 3).
Как
известно, шкала задается группой допустимых преобразований (прямой в себя). Номинальная
шкала (шкала наименований) задается группой всех взаимно-однозначных преобразований,
шкала порядка - группой всех строго возрастающих преобразований. Это - шкалы качественных
признаков. Группа линейных возрастающих преобразований ![]() задает
шкалу интервалов. Группа
задает
шкалу интервалов. Группа ![]() определяет
шкалу отношений. Наконец, группа, состоящая из одного тождественного преобразования,
описывает абсолютную шкалу. Это - шкалы количественных признаков. Используют и некоторые
другие шкалы.
определяет
шкалу отношений. Наконец, группа, состоящая из одного тождественного преобразования,
описывает абсолютную шкалу. Это - шкалы количественных признаков. Используют и некоторые
другие шкалы.
Практическую
пользу теории измерений обычно демонстрируют на примере задачи сравнения средних
значений для двух совокупностей одинакового объема x1,
x2,…,xn и y1, y2,…,yn. Пусть среднее вычисляется с помощью функции ![]() Если
Если
f(x1, x2,…,xn)<f(y1, y2,…,yn),. (13)
то необходимо, чтобы
![]() (14)
(14)
для
любого допустимого преобразования ![]() из задающей
шкалу группы
из задающей
шкалу группы ![]() . (В противном
случае результат сравнения будет зависеть от того, какое из эквивалентных представлений
шкалы выбрал исследователь.)
. (В противном
случае результат сравнения будет зависеть от того, какое из эквивалентных представлений
шкалы выбрал исследователь.)
Требование равносильности неравенств (13) и (14) вместе с некоторыми условиями регулярности приводят к тому, что в порядковой шкале в качестве средних можно использовать только члены вариационного ряда, в частности, медиану, но нельзя использовать среднее геометрическое, среднее арифметическое, и т.д. В количественных шкалах это требование выделяет из всех обобщенных средних по А.Н. Колмогорову в шкале интервалов - только среднее арифметическое, а в шкале отношений - только степенные средние. Кроме средних, аналогичные задачи рассмотрены для расстояний, мер связи случайных признаков и других процедур анализа данных.
Приведенные результаты о средних величинах применялись, например, при проектировании системы датчиков в АСУ ТП доменных печей. Велико прикладное значение теории измерений в задачах стандартизации и управления качеством, в частности, в квалиметрии. Так, В.В. Подиновский показал, что любое изменение коэффициентов весомости единичных показателей качества продукции приводит к изменению упорядочения изделий по средневзвешенному показателю, а Н.В. Хованов развил одну из возможных теорий шкал измерения качества. Теория измерений полезна и в других прикладных областях.
Статистика бинарных отношений. Оценивание центра распределения случайного бинарного отношения проводят обычно с помощью медианы Кемени. Состоятельность вытекает из закона больших чисел [3]. Вычислительные процедуры нахождения медианы Кемени здесь не обсуждаем.
Методы проверки гипотез развиты отдельно для каждой разновидности бинарных отношений. В области статистики ранжировок, или ранговой корреляции, классической является книга Кендалла [6]. Современные достижения отражены в работах Ю.Н.Тюрина и Д.С.Шмерлинга. Статистика случайных разбиений развита А.В.Маамяги. Статистика случайных толерантностей (рефлексивных симметричных отношений) изложена в работе [3]. Многие ее задачи являются частными случаями задач теории люсианов.
Теория люсианов (бернуллиевских векторов). Люсиан (бернуллиевский вектор) - это последовательность испытаний Бернулли с, вообще говоря, различными вероятностями успеха. Реализация люсиана (бернуллиевского вектора) - это последовательность из 0 и 1. Люсианы (бернуллиевские вектора) рассматривались как случайные множества с независимыми элементами, а также - как результаты независимых парных сравнений. Последовательность результатов контроля качества последовательности единиц продукции по альтернативному признаку - также реализация люсиана (бернуллиевского вектора). Случайная толерантность может быть записана в виде люсиана. Поскольку один и тот же эконометрический объект применяется в различных областях, естественно для его наименования применять специально введенный термин "бернуллиевский вектор". Используется также термин "люсиан".
В рассматриваемой теории изучают методы проверки согласованности (одинаковой распределенности), однородности двух выборок, независимости люсианов. Методы проверки указанных гипотез нацелены на ситуацию, когда число бернуллиевских векторов фиксировано, а их длина растет. При этом число неизвестных параметров возрастает пропорционально объему данных, т.е. теория построена в асимптотике растущего числа параметров. Ранее подобная асимптотика под названием асимптотики А.Н.Колмогорова использовалась в дискриминантном анализе, но там применялись совсем другие методы.
Непараметрическая теория парных сравнений (в предположении независимости результатов отдельных сравнений) - часть теории бернуллиевских векторов. Параметрическая теория связана в основном с попытками выразить вероятности того или иного исхода через значения гипотетических или реальных параметров сравниваемых объектов. Известны модели Терстоуна, Бредли-Терри-Льюса и др.. В СССР построен ряд новых моделей парных сравнений (см. выше - второй пункт настоящей главы). Имеются модели парных сравнений с тремя исходами (больше, меньше, неразличимо), модели зависимых сравнений, сравнений нескольких объектов (сближающие рассматриваемую область с теорией случайных ранжировок) и т.д.
Статистика случайных и нечетких множеств. Давнюю историю имеет статистика случайных геометрических объектов (отрезков, треугольников, кругов и т.д.). Современная теория случайных множеств сложилась при изучении пористых сред и объектов сложной природы в таких областях, как металлография, петрография, биология. Различные направления внутри этой теории рассмотрены в работе [3, гл.4]. Остановимся на двух.
Случайные
множества, лежащие в евклидовом пространстве, можно складывать: сумма множеств A и B- - это объединение всех векторов x+y, где ![]() Н.Н. Ляшенко
получил аналоги законов больших чисел, центральной предельной теоремы, ряда методов
прикладной статистики, систематически используя подобные суммы.
Н.Н. Ляшенко
получил аналоги законов больших чисел, центральной предельной теоремы, ряда методов
прикладной статистики, систематически используя подобные суммы.
Для статистики объектов нечисловой природы интереснее подмножества пространств, не являющихся линейными. В работе [3] рассмотрены некоторые задачи теории конечных случайных множеств. Ряд интересных результатов получил С.А.Ковязин, в частности, он доказал нашу гипотезу о справедливости закона больших чисел при использовании расстояния между множествами
![]() (15)
(15)
где
![]() - некоторая
мера;.
- некоторая
мера;.![]() - знак симметрической
разности. Расстояние (15) выведено из некоторой системы аксиом в монографии [3].
Прикладники также делают попытки развивать методы статистики случайных множеств.
- знак симметрической
разности. Расстояние (15) выведено из некоторой системы аксиом в монографии [3].
Прикладники также делают попытки развивать методы статистики случайных множеств.
С теорией случайных множеств тесно связана теория нечетких множеств, начало которой положено статьей Л.А.Заде 1965 г. Это направление прикладной математики получило бурное развитие - к настоящему времени число публикаций измеряется десятками тысяч, имеются международные журналы, постоянно проводятся конференции, практические приложения дали ощутимый технико-экономический эффект. При изложении теории нечетких множеств обычно не подчеркивается связь с вероятностными моделями. Между тем еще в первой половине 1970-х годов было установлено [3], что теория нечеткости в определенном смысле сводится к теории случайных множеств, хотя эта связь и имеет лишь теоретическое значение.
С точки зрения статистики объектов нечисловой природы нечеткие множества - лишь один из видов объектов нечисловой природы. Поэтому к ним применима общая теория в пространствах произвольной природы. Имеются работы, в которых совместно используются соображения вероятности и нечеткости.
Многомерное шкалирование и аксиоматическое введение метрик. Многомерное шкалирование имеет целью представление объектов точками в пространстве небольшой размерности (1-3) с максимально возможным сохранением расстояний между точками.
Из сказанного выше ясно, какое большое место занимают в статистике объектов нечисловой природы метрики (расстояния). Как их выбрать? Предлагают выводить вид метрик из некоторых систем аксиом. Аксиоматически получена метрика в пространстве ранжировок, которая оказалась линейно связанной с коэффициентом ранговой корреляции Кендалла. Метрика (15) в пространстве множеств получена в работе [3] также исходя из некоторой системы аксиом. Г.В.Раушенбахом [23] дана сводка по аксиоматическому подходу к введению метрик в пространствах нечисловой природы. К настоящему времени практически для каждой используемой в прикладных работах метрики удалось подобрать систему аксиом, из которой чисто математическими средствами можно вывести именно эту метрику.
Применения статистики объектов нечисловой природы. Идеи, подходы, результаты статистики объектов нечисловой природы оказались полезными и в классических областях прикладной статистики. Статистика в пространствах общей природы позволила с единых позиций рассмотреть всю прикладную статистику, в частности, показать, что регрессионный, дисперсионный и дискриминантный анализы являются частными случаями общей схемы регрессионного анализа в пространстве произвольной природы. Поскольку структура модели - объект нечисловой природы, то ее оценивание, в частности, оценивание степени полинома в регрессии, также относится к статистике объектов нечисловой природы. Если учесть, что результаты измерения всегда имеют погрешность, т.е. являются не числами, а интервалами или нечеткими множествами, то приходим к необходимости пересмотреть некоторые выводы теоретической статистики. Например, отсутствует состоятельность оценок, нецелесообразно увеличивать объем выборок сверх некоторого предела (см. главу 9).
Технико-экономическая эффективность от применения методов статистики объектов нечисловой природы достаточно высока [114]. К сожалению, из-за изменения экономической ситуации, в частности, из-за инфляции трудно сопоставить конкретные экономические результаты в разные моменты времени. Кроме того, методы статистики объектов нечисловой природы составляют часть эконометрических методов, а те, в свою очередь - часть методов, входящих в систему информационной поддержки принятия решений на предприятии. Какую часть приращения прибыли предприятия надо отнести на эту систему? Мы знаем, как работает система управления фирмой в настоящем виде, но можем только гадать (а точнее, оценивать, скорее всего, с помощью экспертных оценок), каковы были бы результаты финансово-хозяйственной деятельности предприятия, если бы система управления фирмой была бы иной, например, не содержала методов статистики объектов нечисловой природы.
8.4. Законы больших чисел и состоятельность статистических оценок
в пространствах произвольной природы
Законы больших чисел состоят в том, что эмпирические средние сходятся к теоретическим. В классическом варианте: выборочное среднее арифметическое при определенных условиях сходится по вероятности при росте числа слагаемых к математическому ожиданию. На основе законов больших чисел обычно доказывают состоятельность различных статистических оценок. В целом эта тематика занимает заметное место в теории вероятностей и математической статистике.
Однако математический аппарат при этом основан на свойствах сумм случайных величин (векторов, элементов линейных пространств). Следовательно, он не пригоден для изучения вероятностных и статистических проблем, связанных со случайными объектами нечисловой природы. Это такие объекты, как бинарные отношения, нечеткие множества, вообще элементы пространств без векторной структуры. Объекты нечисловой природы все чаще встречаются в прикладных исследованиях. Много конкретных примеров приведено выше в настоящей главе. Поэтому представляется полезным получение законов больших чисел в пространствах нечисловой природы. Необходимо решить следующие задачи.
А) Определить понятие эмпирического среднего.
Б) Определить понятие теоретического среднего.
В) Ввести понятие сходимости эмпирических средних к теоретическому.
Г) Доказать при тех или иных комплексах условий сходимость эмпирических средних к теоретическому.
Д) Обобщив это доказательство, получить метод обоснования состоятельности различных статистических оценок.
Е) Дать применения полученных результатов при решении конкретных задач.
Ввиду принципиальной важности рассматриваемых результатов приводим доказательство закона больших чисел, а также результаты компьютерного анализа множества эмпирических средних.
Определения средних величин. Пусть X - пространство произвольной природы,
x1, x2, x3,...,xn - его элементы. Чтобы ввести эмпирическое среднее
для x1, x2, x3,...,xn будем
использовать действительнозначную (т.е. с числовыми значениями) функцию f(x,y)
двух переменных со значениями в X. В стандартных математических обозначениях,
![]() Величина f(x,y) интерпретируется как показатель
различия между x и y: чем f(x,y) больше, тем x и y
сильнее различаются. В качестве f можно использовать расстояние в Х,
квадрат расстояния и т.п.
Величина f(x,y) интерпретируется как показатель
различия между x и y: чем f(x,y) больше, тем x и y
сильнее различаются. В качестве f можно использовать расстояние в Х,
квадрат расстояния и т.п.
Определение 1. Средней величиной для совокупности x1, x2, x3,...,xn (относительно меры различия f), обозначаемой любым из трех способов:
хср = En(f) = En(x1, x2, x3,...,xn ; f) ,
называем решение оптимизационной задачи
![]()
Это определение согласуется с классическим: если Х = R1, f(x,y) = (x - y)2, то хср - выборочное среднее арифметическое. Если же Х = R1, f(x,y) = |x - y|, то при n = 2k+1 имеем хср = x(k+1), при n= 2k эмпирическое среднее является отрезком [x(k), x(k+1)]. Здесь через x(i) обозначен i-ый член вариационного ряда, построенного по x1, x2, x3,...,xn, т.е. i-я порядковая статистика. Таким образом, при Х = R1, f(x,y) = |x - y| решение задачи (1) дает естественное определение выборочной медианы, правда, несколько отличающееся от предлагаемого в курсах "Общей теории статистики", в котором при n= 2k медианой называют полусумму двух центральных членов вариационного ряда (x(k) + x(k+1))/2. Иногда x(k) называют левой медианой , а х(k+1) - правой медианой [3].
Решением задачи (1) является множество En(f), которое может быть пустым, состоять из одного или многих элементов. Выше приведен пример, когда решением является отрезок. Если Х = R1 \ {х0} , f(x,y) = (x - y)2 , а среднее арифметическое выборки равно х0, то En(f) пусто.
При моделировании реальных ситуаций часто можно принять, что Х состоит из конечного числа элементов, а тогда En(f) непусто - минимум на конечном множестве всегда достигается.
Понятия
случайного элемента ![]() со значениями в Х, его распределения, независимости
случайных элементов используем согласно пункту 2 настоящей главы, т.е. справочнику
Ю.В. Прохорова и Ю.А. Розанова [25]. Будем считать, что функция f измерима
относительно
со значениями в Х, его распределения, независимости
случайных элементов используем согласно пункту 2 настоящей главы, т.е. справочнику
Ю.В. Прохорова и Ю.А. Розанова [25]. Будем считать, что функция f измерима
относительно ![]() -алгебры, участвующей в определении случайного элемента
-алгебры, участвующей в определении случайного элемента
![]() . Тогда
. Тогда ![]() при фиксированном y является действительнозначной
случайной величиной. Предположим, что она имеет математическое ожидание.
при фиксированном y является действительнозначной
случайной величиной. Предположим, что она имеет математическое ожидание.
Определение 2. Теоретическим средним (математическим ожиданием) для случайного элемента
![]() относительно меры различия f, обозначаемом
E(x,f), называется решение оптимизационной задачи
относительно меры различия f, обозначаемом
E(x,f), называется решение оптимизационной задачи
![]()
Это
определение также согласуется с классическим. Если Х = R1, f(x,y)
= (x - y)2, то E(x,f) = E(x) - обычное математическое ожидание,
при этом E![]() - дисперсия случайной величины
- дисперсия случайной величины ![]() . Если же Х = R1 , f(x,y) = |x - y|
, то E(x,f) = [a,b], где a = sup{t: F(t)<0,5}, b = inf{t:
F(t)>0,5}, причем F(t) - функция распределения случайной величины
. Если же Х = R1 , f(x,y) = |x - y|
, то E(x,f) = [a,b], где a = sup{t: F(t)<0,5}, b = inf{t:
F(t)>0,5}, причем F(t) - функция распределения случайной величины
![]() . Если график F(t) имеет плоский участок на
уровне F(t) = 0,5, то медиана - теоретическое среднее в смысле определения
2 - является отрезком. В классическом случае обычно говорят, что каждый элемент
отрезка [a; b] является одним из возможных значений медианы. Поскольку наличие
указанного плоского участка - исключительный случай, то обычно решением задачи
(2) является множество из одного элемента a = b - классическая медиана распределения
случайной величины
. Если график F(t) имеет плоский участок на
уровне F(t) = 0,5, то медиана - теоретическое среднее в смысле определения
2 - является отрезком. В классическом случае обычно говорят, что каждый элемент
отрезка [a; b] является одним из возможных значений медианы. Поскольку наличие
указанного плоского участка - исключительный случай, то обычно решением задачи
(2) является множество из одного элемента a = b - классическая медиана распределения
случайной величины ![]() .
.
Теоретическое
среднее E(x,f) можно определить лишь тогда, когда ![]() существует при всех
существует при всех ![]() . Оно может быть пустым множеством, например, если
Х = R1 \ {х0}
, f(x,y) = (x - y)2 , x0= E(x). И то, и другое исключается, если Х конечно.
Однако и для конечных Х теоретическое среднее может состоять не из одного,
а из многих элементов. Отметим, однако, что в множестве всех распределений вероятностей
на Х подмножество тех распределений, для которых E(x,f) состоит более
чем из одного элемента, имеет коразмерность 1, поэтому основной является ситуация,
когда множество E(x,f) содержит единственный элемент [3].
. Оно может быть пустым множеством, например, если
Х = R1 \ {х0}
, f(x,y) = (x - y)2 , x0= E(x). И то, и другое исключается, если Х конечно.
Однако и для конечных Х теоретическое среднее может состоять не из одного,
а из многих элементов. Отметим, однако, что в множестве всех распределений вероятностей
на Х подмножество тех распределений, для которых E(x,f) состоит более
чем из одного элемента, имеет коразмерность 1, поэтому основной является ситуация,
когда множество E(x,f) содержит единственный элемент [3].
Существование средних величин. Под существованием средних величин будем понимать непустоту множеств решений соответствующих оптимизационных задач.
Если Х состоит из конечного числа элементов, то минимум в задачах (1) и (2) берется по конечному множеству, а потому, как уже отмечалось, эмпирические и теоретические средние существуют.
Ввиду важности обсуждаемой темы приведем доказательства. Для строгого математического изложения нам понадобятся термины из раздела математики под названием "общая топология". Топологические термины и результаты будем использовать в соответствии с классической монографией [29]. Так, топологическое пространство называется бикомпактным в том и только в том случае, когда из каждого его открытого покрытия можно выбрать конечное подпокрытие [29, с.183]..
Теорема 1. Пусть Х - бикомпактное пространство, функция f непрерывна на Х2 (в топологии произведения). Тогда эмпирическое и теоретическое средние существуют.
Доказательство. Функция f(xi,y) от y непрерывна, сумма непрерывных функций непрерывна, непрерывная функция на бикомпакте достигает своего минимума, откуда и следует заключение теоремы относительно эмпирического среднего.
Перейдем
к теоретическому среднему. По теореме Тихонова [29, с.194] из бикомпактности Х
вытекает бикомпактность Х2. Для каждой точки (x, y) из
Х2 рассмотрим ![]() - окрестность в Х2 в
смысле показателя различия f, т.е. множество
- окрестность в Х2 в
смысле показателя различия f, т.е. множество
![]()
Поскольку f непрерывна, то множества U(x,y) открыты в рассматриваемой топологии в Х2. По теореме Уоллеса [29, с.193] существуют открытые (в Х) множества V(x) и W(y), содержащие x и y соответственно и такие, что их декартово произведение V(x) x W(y) целиком содержится внутри U(x, y).
Рассмотрим покрытие Х2 открытыми множествами V(x) x W(y). Из бикомпактности Х2 вытекает существование конечного подпокрытия {V(xi) x W(yi), i = 1,2,...,m}. Для каждого х из Х рассмотрим все декартовы произведения V(xi) x W(yi), куда входит точка (x, y) при каком-либо y. Таких декартовых произведений и их первых множителей V(xi) конечное число. Возьмем пересечение таких первых множителей V(xi) и обозначим его Z(x). Это пересечение открыто, как пересечение конечного числа открытых множеств, и содержит точку х. Из покрытия бикомпактного пространства X открытыми множествами Z(x) выберем открытое подпокрытие Z1, Z2, ..., Zk.
Покажем,
что если ![]() и
и ![]() принадлежат одному и тому же Zj
при некотором j, то
принадлежат одному и тому же Zj
при некотором j, то
![]() (3)
(3)
Пусть
Zj = Z(x0)
при некотором x0. Пусть V(xi) x W(yi),
![]() , - совокупность всех тех исходных декартовых произведений
из системы {V(xi) x W(yi), i = 1,2,...,m}, куда входят
точки (x0, y) при различных y. Покажем, что их объединение
содержит также точки
, - совокупность всех тех исходных декартовых произведений
из системы {V(xi) x W(yi), i = 1,2,...,m}, куда входят
точки (x0, y) при различных y. Покажем, что их объединение
содержит также точки ![]() и
и ![]() при всех y. Действительно, если (х0, y)
входит в V(xi) x W(yi), то y входит в W(yi),
а
при всех y. Действительно, если (х0, y)
входит в V(xi) x W(yi), то y входит в W(yi),
а ![]() и
и ![]() вместе
с x0 входят
в V(xi), поскольку
вместе
с x0 входят
в V(xi), поскольку ![]() ,
, ![]() и
x0 входят
в Z(x0).
Таким образом,
и
x0 входят
в Z(x0).
Таким образом, ![]() и
и ![]() принадлежат V(xi) x W(yi),
а потому согласно определению V(xi) x W(yi)
принадлежат V(xi) x W(yi),
а потому согласно определению V(xi) x W(yi)
![]()
откуда и следует неравенство (3).
Поскольку
Х2 - бикомпактное пространство, то функция f
ограничена на Х2 , а потому существует математическое
ожидание E f(![]() ,y)
для любого случайного элемента
,y)
для любого случайного элемента ![]() , удовлетворяющего приведенным в предыдущем разделе
условиям согласования топологии, связанной с f, и измеримости, связанной
с
, удовлетворяющего приведенным в предыдущем разделе
условиям согласования топологии, связанной с f, и измеримости, связанной
с ![]() . Если х1 и х2
принадлежат одному открытому множеству Zj , то
. Если х1 и х2
принадлежат одному открытому множеству Zj , то
![]()
а потому функция
g(y) = E f(![]() ,y) (4)
,y) (4)
непрерывна
на Х. Поскольку непрерывная функция на бикомпактном множестве достигает своего
минимума, т.е. существуют такие точки z, на которых g(z) = inf{g(y),
y![]() X},
то теорема 1 доказана.
X},
то теорема 1 доказана.
В ряде интересных для приложений ситуаций Х не является бикомпактным пространством. Например, если Х = R1. В этих случаях приходится наложить на показатель различия f некоторые ограничения, например, так, как это сделано в теореме 2.
Теорема
2. Пусть Х - топологическое пространство, непрерывная (в топологии произведения)
функция f: X2![]() R1 неотрицательна, симметрична (т.е. f(x,y) = f (y,x) для любых
x и y из X), существует число D>0 такое, что при
всех x,y,z из X
R1 неотрицательна, симметрична (т.е. f(x,y) = f (y,x) для любых
x и y из X), существует число D>0 такое, что при
всех x,y,z из X
f(x,y) < D{f(x,z) + f(z,y)}. (5)
Пусть
в Х существует точка x0
такая, что при любом положительном
R множество{x: f(x, x0) <R} является бикомпактным. Пусть
для случайного элемента ![]() , согласованного с топологией в рассмотренном выше
смысле, существует g(x0)
= Ef(
, согласованного с топологией в рассмотренном выше
смысле, существует g(x0)
= Ef(![]() , x0 ).
, x0 ).
Тогда существуют (т.е. непусты) математическое ожидание E(x,f) и эмпирические средние En(f).
Замечание. Условие (5) - некоторое обобщение неравенства треугольника. Например, если g - метрика в X, а f = gp при некотором натуральном p, то для f выполнено соотношение (5) с D = 2p.
Доказательство. Рассмотрим функцию g(y), определенную формулой (4). Имеем
f(![]() ,y) < D {f(
,y) < D {f(![]() , x0) + f(x0,,y)}. (6)
, x0) + f(x0,,y)}. (6)
Поскольку по условию теоремы g(x0) существует, а потому конечно, то из оценки (6) следует существование и конечность g(y) при всех y из Х. Докажем непрерывность этой функции.
Рассмотрим шар (в смысле меры различия f ) радиуса R с центром в x0:
K(R) = {x : f(x, x0) < R}, R > 0.
В соответствии с условием теоремы K(R) как подпространство топологического пространства Х является бикомпактным. Рассмотрим произвольную точку х из Х. Справедливо разложение
![]()
где
![]() (С) -
индикатор множества С. Следовательно,
(С) -
индикатор множества С. Следовательно,
![]() (7)
(7)
Рассмотрим второе слагаемое в (7). В силу (5)
![]() (8)
(8)
Возьмем математическое ожидание от обеих частей (8):
![]() (9)
(9)
В правой части (9) оба слагаемых стремятся к 0 при безграничном возрастании R: первое - в силу того, что
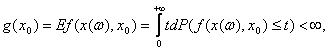
второе
- в силу того, что распределение случайного элемента ![]() сосредоточено на Х и
сосредоточено на Х и
![]()
Пусть U(x) - такая окрестность х (т.е. открытое множество, содержащее х), для которой
sup {f(y, x), y![]() U(x)}
<
U(x)}
<![]()
Имеем
![]() (10)
(10)
В силу (9) и (10) при безграничном возрастании R
![]() (11)
(11)
равномерно
по y![]() U(x).
Пусть R(0) таково, что левая часть (11) меньше
U(x).
Пусть R(0) таково, что левая часть (11) меньше ![]() >
0 при R>R(0) и, кроме того, y
>
0 при R>R(0) и, кроме того, y![]() U(x)
U(x)![]() K(R(0)).
Тогда при R>R(0)
K(R(0)).
Тогда при R>R(0)
![]() (12)
(12)
Нас
интересует поведение выражения в правой части формулы (12) при y![]() U(x).
Рассмотрим f1 - сужение функции f на замыкание
декартова произведения множеств U(x) х K(R), и случайный элемент
U(x).
Рассмотрим f1 - сужение функции f на замыкание
декартова произведения множеств U(x) х K(R), и случайный элемент ![]() Тогда
Тогда
![]()
при
y![]() U(x),
а непрерывность функции
U(x),
а непрерывность функции ![]() была доказана
в теореме 1. Последнее означает, что существует окрестность U1(x)
точки х такая, что
была доказана
в теореме 1. Последнее означает, что существует окрестность U1(x)
точки х такая, что
![]() (13)
(13)
при
y![]() U1(x).
Из (12) и (13) вытекает, что при
U1(x).
Из (12) и (13) вытекает, что при ![]()
![]()
что и доказывает непрерывность функции g(x).
Докажем существование математического ожидания E(x,f). Пусть R(0) таково, что
![]() (14)
(14)
Пусть
H - некоторая константа, значение которой будет выбрано позже. Рассмотрим
точку х из множества K(HR(0))С - дополнения K(HR(0)),
т.е. из внешности шара радиуса HR(0) с центром в х0. Пусть ![]() Тогда имеем
Тогда имеем
![]()
откуда
![]() (15)
(15)
Выбирая
H достаточно большим, получим с учетом условия (14), что при x![]() K(HR(0))С справедливо неравенство
K(HR(0))С справедливо неравенство
![]() (16)
(16)
Можно
выбрать H так, чтобы правая часть (16) превосходила ![]()
Сказанное означает, что Argmin g(x) достаточно искать внутри бикомпактного множества K(HR(0)). Из непрерывности функции g вытекает, что ее минимум достигается на указанном бикомпактном множестве, а потому - и на всем Х. Существование (непустота) теоретического среднего E(x,f) доказана.
Докажем
существование эмпирического среднего En(f). Есть искушение проводить
его дословно так же, как и доказательство существования математического ожидания
E(x,f), лишь с заменой 1/2 в формуле (16) на частоту попадания элементов
выборки xi в шар K(R(0)), каковая, очевидно,
стремится к вероятности попадания случайного элемента ![]() в
K(R(0)), большей 1/2 в соответствии с (14). Однако это рассуждение показывает
лишь, что вероятность непустоты En(f) стремится к 1 при безграничном
росте объема выборки. Точнее, оно показывает, что
в
K(R(0)), большей 1/2 в соответствии с (14). Однако это рассуждение показывает
лишь, что вероятность непустоты En(f) стремится к 1 при безграничном
росте объема выборки. Точнее, оно показывает, что
![]()
Поэтому пойдем другим путем, не опирающимся к тому же на вероятностную модель выборки. Положим
![]() (17)
(17)
Если х входит в дополнение шара K(HR(1)), то аналогично (15) имеем
![]() (18)
(18)
При достаточно большом H из (17) и (18) следует, что
![]()
Следовательно, Argmin достаточно искать на K(HR(1)). Заключение теоремы 2 следует из того, что на бикомпактном пространстве K(HR(1)) минимизируется непрерывная функция.
Теорема 2 полностью доказана.
О формулировках законов больших чисел. Пусть ![]() - независимые
одинаково распределенные случайные элементы со значениями в Х. Закон больших
чисел - это утверждение о сходимости эмпирических средних к теоретическому среднему
(математическому ожиданию) при росте объема выборки n, т.е. утверждение о
том, что
- независимые
одинаково распределенные случайные элементы со значениями в Х. Закон больших
чисел - это утверждение о сходимости эмпирических средних к теоретическому среднему
(математическому ожиданию) при росте объема выборки n, т.е. утверждение о
том, что
![]() (19)
(19)
при
![]() . Однако
и слева, и справа в формуле (19) стоят, вообще говоря, множества. Поэтому понятие
сходимости в (19) требует обсуждения и определения.
. Однако
и слева, и справа в формуле (19) стоят, вообще говоря, множества. Поэтому понятие
сходимости в (19) требует обсуждения и определения.
В
силу классического закона больших чисел при ![]()
![]() (20)
(20)
в смысле сходимости по вероятности, если правая часть существует (теорема А.Я. Хинчина, 1923 г.).
Если пространство Х состоит из конечного числа элементов, то из соотношения (20) легко вытекает (см., например, [3, с.192-193]), что
![]() (21)
(21)
Другими
словами, ![]() является
состоятельной оценкой
является
состоятельной оценкой ![]() .
.
Если
![]() состоит
из одного элемента,
состоит
из одного элемента, ![]() , то соотношение
(21) переходит в следующее:
, то соотношение
(21) переходит в следующее:
![]() (22)
(22)
Однако
с прикладной точки зрения доказательство соотношений (21)-(22) не дает достаточно
уверенности в возможности использования ![]() в качестве
оценки E(x,f), поскольку в процессе доказательства объем выборки предполагается
настолько большим, что при всех y
в качестве
оценки E(x,f), поскольку в процессе доказательства объем выборки предполагается
настолько большим, что при всех y![]() X одновременно
левые части соотношений (20) сосредотачиваются в непересекающихся окрестностях правых
частей.
X одновременно
левые части соотношений (20) сосредотачиваются в непересекающихся окрестностях правых
частей.
Замечание.
Если в соотношении (20) рассмотреть сходимость с вероятностью 1, то аналогично
(21) получим т.н. усиленный закон больших чисел [3, с.193-194], согласно которому
с вероятностью 1 эмпирическое среднее ![]() входит в
теоретическое среднее E(x,f), начиная с некоторого объема выборки n,
вообще говоря, случайного,
входит в
теоретическое среднее E(x,f), начиная с некоторого объема выборки n,
вообще говоря, случайного, ![]() . Мы не будем
останавливаться на этом виде сходимости, поскольку в соответствующих постановках,
подробно разобранных в монографии [3], нет принципиальных отличий от случая сходимости
по вероятности.
. Мы не будем
останавливаться на этом виде сходимости, поскольку в соответствующих постановках,
подробно разобранных в монографии [3], нет принципиальных отличий от случая сходимости
по вероятности.
Если
Х не является конечным, например, Х = R1 ,
то соотношения (21) и (22) неверны. Поэтому необходимо искать иные формулировки
закона больших чисел. В классическом случае сходимости выборочного среднего арифметического
к математическому ожиданию, т.е. ![]() можно записать
закон больших чисел так: для любого
можно записать
закон больших чисел так: для любого ![]() > 0 справедливо
предельное соотношение
> 0 справедливо
предельное соотношение
![]() (23)
(23)
В
этом соотношении в отличие от (21) речь идет о попадании эмпирического среднего
![]() =
=![]() не непосредственно
внутрь теоретического среднего E(x,f), а в некоторую окрестность теоретического
среднего.
не непосредственно
внутрь теоретического среднего E(x,f), а в некоторую окрестность теоретического
среднего.
Обобщим эту формулировку. Как задать окрестность теоретического
среднего в пространстве произвольной природы? Естественно взять его окрестность,
определенную с помощью какой-либо метрики. Однако полезно обеспечить на ее дополнении
до Х отделенность множества значений Ef(x(![]() ),y)
как функции y от минимума этой функции на всем Х.
),y)
как функции y от минимума этой функции на всем Х.
Поэтому
мы сочли целесообразным определить такую окрестность с помощью самой функции Ef(x(![]() ),y).
),y).
Определение
3. Для любого ![]() > 0 назовем
> 0 назовем
![]() -пяткой функции
g(x) множество
-пяткой функции
g(x) множество
![]()
Таким
образом, в ![]() -пятку входят
все те х, для которых значение g(x) либо минимально, либо отличается
от минимального (или от инфимума) не более чем на
-пятку входят
все те х, для которых значение g(x) либо минимально, либо отличается
от минимального (или от инфимума) не более чем на ![]() . Так, для
X = R1 и функции g(x) = х2 минимум
равен 0, а
. Так, для
X = R1 и функции g(x) = х2 минимум
равен 0, а ![]() -пятка имеет
вид интервала
-пятка имеет
вид интервала ![]() . В формулировке
(23) классического закона больших чисел утверждается, что при любом
. В формулировке
(23) классического закона больших чисел утверждается, что при любом ![]() >0 вероятность
попадания среднего арифметического в
>0 вероятность
попадания среднего арифметического в ![]() -пятку математического
ожидания стремится к 1. Поскольку
-пятку математического
ожидания стремится к 1. Поскольку ![]() > 0 произвольно,
то вместо
> 0 произвольно,
то вместо ![]() -пятки можно
говорить о
-пятки можно
говорить о ![]() -пятке, т.е.
перейти от (23) к эквивалентной записи
-пятке, т.е.
перейти от (23) к эквивалентной записи
![]() (24)
(24)
Соотношение (24) допускает непосредственное обобщение на общий случай пространств произвольной природы.
СХЕМА
ЗАКОНА БОЛЬШИХ ЧИСЕЛ. Пусть ![]() - независимые
одинаково распределенные случайные элементы со значениями в пространстве произвольной
природы Х с показателем различия f: X2
- независимые
одинаково распределенные случайные элементы со значениями в пространстве произвольной
природы Х с показателем различия f: X2![]() R1.
Пусть выполнены некоторые математические условия регулярности. Тогда
для любого
R1.
Пусть выполнены некоторые математические условия регулярности. Тогда
для любого ![]() > 0 справедливо
предельное соотношение
> 0 справедливо
предельное соотношение
![]() (25)
(25)
Аналогичным образом может быть сформулирована и общая идея усиленного закона больших чисел. Ниже приведены две конкретные формулировки "условий регулярности".
Законы больших чисел. Начнем с рассмотрения естественного обобщения конечного множества - бикомпактного пространства Х.
Теорема 3. В условиях теоремы 1 справедливо соотношение (25).
Доказательство. Воспользуемся построенным при доказательстве теоремы 1 конечным открытым покрытием {Z1, Z2, ..., Zk} пространства Х таким, что для него выполнено соотношение (3). Построим на его основе разбиение Х на непересекающиеся множества W1, W2, ..., Wm (объединение элементов разбиения W1, W2, ..., Wm составляет Х). Это можно сделать итеративно. На первом шаге из Z1 следует вычесть Z2, ..., Zk - это и будет W1 . Затем в качестве нового пространства надо рассмотреть разность Х и W1 , а покрытием его будет {Z2, ..., Zk} . И так до k-го шага, когда последнее из рассмотренных покрытий будет состоять из единственного открытого множества Zk . Остается из построенной последовательности W1, W2, ..., Wk вычеркнуть пустые множества, которые могли быть получены при осуществлении описанной процедуры (поэтому, вообще говоря, m может быть меньше k).
В каждом из элементов разбиения W1, W2, ..., Wm выберем по одной точке, которые назовем центрами разбиения и соответственно обозначим w1, w2, ..., wm. Это и есть то конечное множество, которым можно аппроксимировать бикомпактное пространство Х. Пусть y входит в Wj . Тогда из соотношения (3) вытекает, что
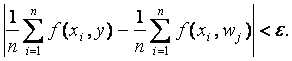 (26)
(26)
Перейдем
к доказательству соотношения (25). Возьмем произвольное ![]() >0.
Рассмотрим некоторую точку b из E(x,f). Доказательство будет основано
на том, что с вероятностью, стремящейся к 1, для любого y вне
>0.
Рассмотрим некоторую точку b из E(x,f). Доказательство будет основано
на том, что с вероятностью, стремящейся к 1, для любого y вне ![]() выполнено
неравенство
выполнено
неравенство
![]() (27)
(27)
Для
обоснования этого неравенства рассмотрим все элементы разбиения W1,
W2, ..., Wm, имеющие непустое пересечение с внешностью
![]() -пятки
-пятки ![]() . Из неравенства
(26) следует, что для любого y вне
. Из неравенства
(26) следует, что для любого y вне ![]() левая часть
неравенства (27) не меньше
левая часть
неравенства (27) не меньше
![]() (28)
(28)
где
минимум берется по центрам всех элементов разбиения, имеющим непустое пересечение
с внешностью ![]() -пятки. Возьмем
теперь в каждом таком разбиении точку vi , лежащую
вне -пятки
-пятки. Возьмем
теперь в каждом таком разбиении точку vi , лежащую
вне -пятки ![]() . Тогда из
неравенств (3) и (28) следует, что левая часть неравенства (27) не меньше
. Тогда из
неравенств (3) и (28) следует, что левая часть неравенства (27) не меньше
![]() (29)
(29)
В силу закона больших чисел для действительнозначных случайных величин каждая из участвующих в соотношениях (27) и (29) средних арифметических имеет своими пределами соответствующие математические ожидания, причем в соотношении (29) эти пределы не менее
![]()
поскольку
точки vi лежат вне ![]() -пятки
-пятки ![]() . Следовательно,
при
. Следовательно,
при
![]()
и достаточно большом n, обеспечивающем необходимую близость рассматриваемого конечного числа средних арифметических к их математическим ожиданиям, справедливо неравенство (27).
Из
неравенства (27) следует, что пересечение En(f) с внешностью ![]() пусто. При
этом точка b может входить в En(f), а может и не входить.
Во втором случае En(f) состоит из иных точек, входящих в
пусто. При
этом точка b может входить в En(f), а может и не входить.
Во втором случае En(f) состоит из иных точек, входящих в ![]() . Теорема
3 доказана.
. Теорема
3 доказана.
Если Х не является бикомпактным пространством, то необходимо суметь оценить рассматриваемые суммы "на периферии", вне бикомпактного ядра, которое обычно выделяется естественным путем. Один из возможных комплексов условий сформулирован выше в теореме 2.
Теорема 4. В условиях теоремы 2 справедлив закон больших чисел, т.е. соотношение (25).
Доказательство. Будем использовать обозначения, введенные в теореме 2 и при ее доказательстве. Пусть r и R, r < R, - положительные числа. Рассмотрим точку х в шаре K(r) и точку y вне шара K(R). Поскольку
![]()
то
![]() (30)
(30)
Положим
![]()
Сравним
![]() и
и ![]() . Выборку
. Выборку
![]()
![]() разобьем
на две части. В первую часть включим те элементы выборки, которые входят в K(r),
во вторую - все остальные (т.е. лежащие вне K(r) ). Множество индексов
элементов первой части обозначим I = I(n,r). Тогда в силу неотрицательности
f имеем
разобьем
на две части. В первую часть включим те элементы выборки, которые входят в K(r),
во вторую - все остальные (т.е. лежащие вне K(r) ). Множество индексов
элементов первой части обозначим I = I(n,r). Тогда в силу неотрицательности
f имеем
![]()
а в силу неравенства (30)
![]()
где Card I(n,r) - число элементов в множестве индексов I(n,r). Следовательно,
![]() (31)
(31)
где
J = Card I(n,r) - биномиальная случайная величина B(n,p) с вероятностью
успеха p = P{![]() }. По теореме
Хинчина для
}. По теореме
Хинчина для ![]() справедлив
(классический) закон больших чисел. Пусть
справедлив
(классический) закон больших чисел. Пусть ![]() . Выберем
. Выберем
![]() так, чтобы
при
так, чтобы
при ![]() было выполнено
соотношение
было выполнено
соотношение
![]() (32)
(32)
где
![]() Выберем
r так, чтобы вероятность успеха p>0,6. По теореме Бернулли можно
выбрать
Выберем
r так, чтобы вероятность успеха p>0,6. По теореме Бернулли можно
выбрать ![]() так, чтобы
при
так, чтобы
при ![]()
![]() (33)
(33)
Выберем R так, чтобы
![]()
Тогда
![]() (34)
(34)
и
согласно (31), (32) и (33) при ![]() с вероятностью
не менее
с вероятностью
не менее ![]() имеем
имеем
![]() (35)
(35)
для
любого y вне K(R). Из (34) следует, что минимизировать ![]() достаточно
внутри бикомпактного шара K(R), при этом En(f) не пусто
и
достаточно
внутри бикомпактного шара K(R), при этом En(f) не пусто
и
![]() (36)
(36)
с
вероятностью не менее 1-2![]() .
.
Пусть
![]() и
и ![]() - сужения
- сужения
![]() и g(x)
= Ef(x(
и g(x)
= Ef(x(![]() ), x)
соответственно на K(R) как функций от х. В силу (34) справедливо равенство
), x)
соответственно на K(R) как функций от х. В силу (34) справедливо равенство
![]() Согласно
доказанной выше теореме 3 найдется
Согласно
доказанной выше теореме 3 найдется ![]() такое, что
такое, что
![]()
Согласно
(36) с вероятностью не менее ![]()
![]()
при
![]() Следовательно,
при
Следовательно,
при ![]() имеем
имеем
![]()
что и завершает доказательство теоремы 4.
Справедливы и иные варианты законов больших чисел, полученные, в частности, в статье [27].
Асимптотическое поведение решений экстремальных статистических задач. Если проанализировать приведенные выше постановки и результаты, особенно теоремы 1 и 3, то становится очевидной возможность их обобщения. Так, доказательства этих теорем практически не меняются, если считать, что функция f(x,y) определена на декартовом произведении бикомпактных пространств X и Y. Тогда можно считать, что элементы выборки лежат в Х, а Y - пространство параметров, подлежащих оценке. Пусть, например, выборка взята из распределения с плотностью p(x,y). Если положить
f(x,y) = - ln p(x,y) ,
то задача нахождения эмпирического среднего переходит в задачу оценивания неизвестного параметра y методом максимального правдоподобия, а законы больших чисел переходят в утверждения о состоятельности этих оценок в случае пространств X и Y общего вида. В случае функции f(x,y) общего вида можно говорить об определении и состоятельности так называемых оценок минимального контраста. Частными случаями этих оценок являются, например, устойчивые (робастные) оценки Тьюки-Хубера (см. главу 10 ниже), оценки параметров в задачах аппроксимации (параметрической регрессии) в пространствах произвольной природы.
Можно пойти и дальше в обобщении законов больших чисел. Пусть известно, что при каждом конкретном y при безграничном росте n имеет быть сходимость по вероятности
fn(x(![]() ), y )
), y )![]() f(y).
f(y).
В каких случаях и в каком смысле
Argmin {fn(x(![]() ),
y ), y
),
y ), y![]() X}
X}![]() Argmin {
f(y), y
Argmin {
f(y), y ![]() X} ?
X} ?
Причем здесь можно под n понимать натуральное число. А можно рассматривать "сходимость по фильтру" в смысле Картана и Бурбаки [29, с.118]. В частности, описывать ситуацию вектором, координаты которого - объемы нескольких выборок, и все они безгранично растут. В классической математической статистике такие постановки рассматривать не любят.
Поскольку, как уже отмечалось, основные задачи прикладной статистики можно представить в виде оптимизационных задач, то ответ на поставленный вопрос дает возможность единообразного подхода к изучению асимптотики решений разнообразных экстремальных статистических задач. Одна из возможных формулировок дана и обоснована выше. Другая - в работе [28]. Она основана на использовании понятий асимптотической равномерной разбиваемости и координатной асимптотической равномерной разбиваемости. С помощью указанных подходов удается стандартным образом обосновывать состоятельность оценок характеристик и параметров в основных задачах прикладной статистики. К сожалению, в рамках настоящей главы нет возможности подробнее остановиться на проблеме оценивания.
Рассматриваемую тематику можно развивать дальше, в частности, рассматривать пространства X и Y, не являющиеся бикомпактными, а также изучать скорость сходимости эмпирических средних к теоретическим.
Медиана Кемени и экспертные оценки. Рассмотрим частный случай пространств нечисловой
природы - пространство бинарных отношений на конечном множестве ![]() и его подпространства.
Как известно, каждое бинарное отношение А можно описать матрицей ||a(i,j)||
из 0 и 1, причем a(i,j) = 1 тогда и только тогда qi и qj
находятся в отношении А, и a(i,j) = 0 в противном случае.
и его подпространства.
Как известно, каждое бинарное отношение А можно описать матрицей ||a(i,j)||
из 0 и 1, причем a(i,j) = 1 тогда и только тогда qi и qj
находятся в отношении А, и a(i,j) = 0 в противном случае.
Определение 4. Расстоянием Кемени между бинарными отношениями А и В, описываемыми матрицами ||a(i,j)|| и ||b(i,j)|| соответственно, называется
![]()
Замечание. Иногда в определение расстояния Кемени вводят множитель, зависящий от k.
Как уже отмечалось, указанное расстояние введено американским исследователем Дж. Кемени в 1950-х годах и получило в нашей стране известность благодаря монографии [24], в которой оно получено для упорядочений (т.е. ранжировок, в которых допускаются связи, или кластеризованных ранжировок - см. главу 12) исходя из некоторой системы аксиом. Некоторое время казалось, что аксиоматический подход избавляет от субъективизма в выборе расстояния, а потому - от субъективизма в выборе способа усреднения бинарных отношений. Монография [24] породила поток работ, в которых с помощью различных систем аксиом вводились те или иные расстояния в пространствах объектов нечисловой природы (в обзоре [23] на эту тему - 161 ссылка на соответствующие публикации). В итоге произвол в выборе метрик отодвинут на уровень произвола в выборе систем аксиом.
Определение 5. Медианой Кемени для выборки, состоящей из бинарных отношений, называется эмпирическое среднее, построенное с помощью расстояния Кемени.
Поскольку число бинарных отношений на конечном множестве конечно, то эмпирические и теоретические средние для произвольных показателей различия существуют и справедливы законы больших чисел, описанные формулами (21) и (22) выше.
Бинарные
отношения, в частности, упорядочения, часто используются для описания мнений экспертов.
Тогда расстояние Кемени измеряет близость мнений экспертов, а медиана Кемени позволяет
находить итоговое усредненное мнение комиссии экспертов. Расчет медианы Кемени обычно
включают в информационное обеспечение систем принятия решений с использованием оценок
экспертов. Речь идет, например, о математическом обеспечении автоматизированного
рабочего места "Математика в экспертизе" (АРМ "МАТЭК"), предназначенного,
в частности, для использования при проведении экспертиз в задачах экологического
страхования. Поэтому представляет большой практический интерес численное изучение
свойств медианы Кемени при конечном объеме выборки. Такое изучение дополняет описанную
выше асимптотическую теорию, в которой объем выборки предполагается безгранично
возрастающим (![]() ).
).
Компьютерное изучение свойств медианы Кемени при конечных объемах выборок. С помощью специально разработанной программной системы В.Н. Жихаревым был проведен ряд серий численных экспериментов по изучению свойств выборочных медиан Кемени. Представление о полученных результатах дается приводимой ниже табл.1, взятой из статьи [30]. В каждой серии методом статистических испытаний определенное число раз моделировался случайный и независимый выбор экспертных ранжировок, а затем находились все медианы Кемени для смоделированного набора мнений экспертов. При этом в сериях 1-5 распределение ответа эксперта предполагалось равномерным на множестве всех ранжировок, а в серии 6 это распределение являлось монотонным относительно расстояния Кемени с некоторым центром (о понятии монотонности см. выше), т.е. вероятность выбора определенной ранжировки убывала с увеличением расстояния Кемени этой ранжировки от центра. Таким образом, серии 1-5 соответствуют ситуации, когда у экспертов нет почвы для согласия, нет группировки их мнений относительно некоторого единого среднего группового мнения, в то время как в серии 6 есть единое мнение - описанный выше центр, к которому тяготеют ответы экспертов.
Результаты, приведенные в табл.1, можно комментировать разными способами. Неожиданным явилось большое число элементов в выборочной медиане Кемени - как среднее, так и особенно максимальное. Одновременно обращает на себя внимание убывание этих чисел при росте числа экспертов и особенно при переходе к ситуации реального существования группового мнения (серия 6). Достаточно часто один из ответов экспертов входит в медиану Кемени (т.е. пересечение множества ответов экспертов и медианы Кемени непусто), а диаметр медианы как множества в пространстве ранжировок заметно меньше диаметра множества ответов экспертов. По этим показателям - наилучшее положение в серии 6. Грубо говоря, всяческие "патологии" в поведении медианы Кемени наиболее резко проявляются в ситуации, когда ее применение не имеет содержательного обоснования, т.е. когда у экспертов нет основы для согласия, их ответы равномерно распределены на множестве ранжировок.
Увеличение числа испытаний в 10 раз при переходе от серии 1 к серии 5 не очень сильно повлияло на приведенные в таблице характеристики, поэтому представляется, что суть дела выявляется при числе испытаний (в методе Монте-Карло), равном 100 или даже 50. Увеличение числа объектов или экспертов увеличивает число элементов в рассматриваемом пространстве ранжировок, а потому уменьшается частота попадания какого-либо из мнений экспертов внутрь медианы Кемени, а также отношение диаметра медианы к диаметру множества экспертов, число элементов медианы Кемени (среднее и максимальное). Можно сказать, что увеличение числа объектов или экспертов уменьшает степень дискретности задачи, приближает ее к непрерывному случаю, а потому уменьшает выраженность различных "патологий".
Есть много интересных результатов, которые мы здесь не рассматриваем. Они связанны, в частности, со сравнением медианы Кемени с другими методами усреднения мнений экспертов, например, с нахождением итогового упорядочения по методу средних рангов, а также с использованием малых окрестностей ответов экспертов для поиска входящих в медиану ранжировок, с теоретической и численной оценкой скорости сходимости в законах больших чисел.
Табл.1. Вычислительный эксперимент по изучению свойств медианы Кемени
|
Номер серии |
1 |
2 |
3 |
4 |
5 |
6 |
|
Число испытаний |
100 |
1000 |
50 |
50 |
1000 |
1000 |
|
Количество объектов |
5 |
5 |
7 |
7 |
5 |
5 |
|
Количество экспертов |
10 |
30 |
10 |
30 |
10 |
10 |
|
Частота непустого пересечения |
0,85 |
0,58 |
0,52 |
0,2 |
0,786 |
0,911 |
|
Среднее отношение диаметров |
0.283 |
0,124 |
0,191 |
0,0892 |
0,202 |
0.0437 |
|
Средняя мощность медианы |
5,04 |
2,41 |
6,4 |
2,88 |
3,51 |
1,35 |
|
Максимальная. мощность медианы |
30 |
14 |
19 |
11 |
40 |
12 |
8.5. Непараметрические оценки плотности в пространствах произвольной природы
Математический аппарат статистики объектов нечисловой природы основан не на свойстве линейности пространства и использовании разнообразных сумм элементов выборок и функций от них, как в классической статистике, а на применении показателей различия, мер близости, метрик, поэтому существенно отличается от классического. В статистике нечисловых данных выделяют общую теорию и статистику в конкретных пространствах нечисловой природы (например, статистику ранжировок). В общей теории есть два основных сюжета. Один связан со средними величинами и асимптотическим поведением решений экстремальных статистических задач, второй - с непараметрическими оценками плотности. Первый сюжет только что рассмотрен, второму посвящена заключительная часть настоящей главы.
Понятие
плотности в пространстве произвольной природы Х требует специального обсуждения.
В пространстве Х должна быть выделена некоторая специальная мера ![]() , относительно
которой будут рассматриваться плотности, соответствующие другим мерам, например,
мере
, относительно
которой будут рассматриваться плотности, соответствующие другим мерам, например,
мере ![]() , задающей
распределение вероятностей некоторого случайного элемента
, задающей
распределение вероятностей некоторого случайного элемента ![]() .
В таком случае
.
В таком случае ![]() (А)
= Р(
(А)
= Р(![]()
![]() А)
для любого случайного события А. Плотность f(x), соответствующая мере
А)
для любого случайного события А. Плотность f(x), соответствующая мере
![]() - это такая
функция, что
- это такая
функция, что
![]()
для
любого случайного события А. Для случайных величин и векторов мера ![]() - это объем
множества А, в математических терминах - мера Лебега. Для дискретных случайных
величин и элементов со значениями в конечном множестве Х в качестве меры
- это объем
множества А, в математических терминах - мера Лебега. Для дискретных случайных
величин и элементов со значениями в конечном множестве Х в качестве меры
![]() естественно
использовать считающую меру, которая событию А ставит в соответствие число
его элементов. Используют также нормированную случайную меру, когда число точек
в множестве А делят на число точек во всем пространстве Х. В случае
считающей меры значение плотности в точке х совпадает с вероятностью попасть
в точку х, т.е. f(x) = Р(ξ = х). Таким образом, с рассматриваемой
точки зрения стирается грань между понятиями «плотность вероятности» и «вероятность
(попасть в точку)».
естественно
использовать считающую меру, которая событию А ставит в соответствие число
его элементов. Используют также нормированную случайную меру, когда число точек
в множестве А делят на число точек во всем пространстве Х. В случае
считающей меры значение плотности в точке х совпадает с вероятностью попасть
в точку х, т.е. f(x) = Р(ξ = х). Таким образом, с рассматриваемой
точки зрения стирается грань между понятиями «плотность вероятности» и «вероятность
(попасть в точку)».
Как могут быть использованы непараметрические оценки плотности распределения вероятностей в пространствах нечисловой природы? Например, для решения задач классификации (диагностики, распознавания образов - см. главу 5). Зная плотности распределения классов, можно решать основные задачи диагностики - как задачи выделения кластеров, так и задачи отнесения вновь поступающего объекта к одному из диагностических классов. В задачах кластер-анализа можно находить моды плотности и принимать их за центры кластеров или за начальные точки итерационных методов типа k-средних или динамических сгущений. В задачах собственно диагностики (дискриминации, распознавания образов с учителем) можно принимать решения о диагностике объектов на основе отношения плотностей, соответствующих классам. При неизвестных плотностях представляется естественным использовать их состоятельные оценки.
Методы оценивания плотности вероятности в пространствах общего вида предложены и первоначально изучены в работе [31]. В частности, в задачах диагностики объектов нечисловой природы предлагаем использовать непараметрические ядерные оценки плотности типа Парзена - Розенблатта (этот вид оценок и его название впервые были введены в статье [31] ). Они имеют вид:
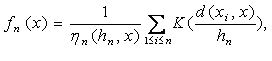
где К: ![]() - так называемая
ядерная функция, x1,
x2, …, xn
- так называемая
ядерная функция, x1,
x2, …, xn ![]() X -
выборка, по которой оценивается плотность, d(xi , x) - показатель
различия (метрика, расстояние, мера близости) между элементом выборки xi
и точкой x, в которой оценивается плотность, последовательность hn
показателей размытости такова, что hn
X -
выборка, по которой оценивается плотность, d(xi , x) - показатель
различия (метрика, расстояние, мера близости) между элементом выборки xi
и точкой x, в которой оценивается плотность, последовательность hn
показателей размытости такова, что hn![]() 0 и nhn
0 и nhn![]() при
при ![]() , а
, а ![]() - нормирующий
множитель, обеспечивающий выполнение условия нормировки (интеграл по всему пространству
от непараметрической оценки плотности fn(x) по мере
- нормирующий
множитель, обеспечивающий выполнение условия нормировки (интеграл по всему пространству
от непараметрической оценки плотности fn(x) по мере ![]() должен равняться
1). Ранее американские исследователи Парзен и Розенблатт использовали подобные статистики
в случае
должен равняться
1). Ранее американские исследователи Парзен и Розенблатт использовали подобные статистики
в случае ![]() с d(xi
, x) = xi - x .
с d(xi
, x) = xi - x .
Введенные описанным образом ядерные оценки плотности - частный случай так называемых линейных оценок, также впервые предложенных в работе [31]. В теоретическом плане они выделяются тем, что удается получать результаты такого же типа, что в классическом одномерном случае, но, разумеется, с помощью совсем иного математического аппарата.
Свойства
непараметрических ядерных оценок плотности. Рассмотрим выборку со значениями в некотором пространстве произвольного
вида. В этом пространстве предполагаются заданными показатель различия d и
мера ![]() . Одна из
основных идей рассматриваемого подхода состоит в том, чтобы согласовать их между
собой. А именно, на их основе построим новый показатель различия d1 ,
так называемый "естественный", в терминах которого проще формулируются
свойства непараметрической оценки плотности. Для этого рассмотрим
шары
. Одна из
основных идей рассматриваемого подхода состоит в том, чтобы согласовать их между
собой. А именно, на их основе построим новый показатель различия d1 ,
так называемый "естественный", в терминах которого проще формулируются
свойства непараметрической оценки плотности. Для этого рассмотрим
шары ![]() радиуса
t>0 и их меры Fx(t) =
радиуса
t>0 и их меры Fx(t) = ![]() (Lt(x)).
Предположим, что Fx(t) как функция t при фиксированном
x непрерывна и строго возрастает. Введем функцию d1(x,y)= Fx(d(x,y)). Это - монотонное преобразование показателя различия
или расстояния, а потому d1(x,y) - также показатель различия (даже если d - метрика,
для d1
неравенство треугольника может
быть не выполнено). Другими словами, d1(x,y),
как и d(x,y), можно рассматривать как показатель различия (меру близости)
между x и y.
(Lt(x)).
Предположим, что Fx(t) как функция t при фиксированном
x непрерывна и строго возрастает. Введем функцию d1(x,y)= Fx(d(x,y)). Это - монотонное преобразование показателя различия
или расстояния, а потому d1(x,y) - также показатель различия (даже если d - метрика,
для d1
неравенство треугольника может
быть не выполнено). Другими словами, d1(x,y),
как и d(x,y), можно рассматривать как показатель различия (меру близости)
между x и y.
Для вновь введенного показателя различия d1(x,y)
введем соответствующие шары ![]() . Поскольку
обратная функция F -1x(t) определена однозначно, то
. Поскольку
обратная функция F -1x(t) определена однозначно, то ![]() ,
где T = F -1x(t).
Следовательно, справедлива цепочка равенств F1x(t) =
,
где T = F -1x(t).
Следовательно, справедлива цепочка равенств F1x(t) = ![]() (L1t(x)) =
(L1t(x)) = ![]() (LT(x))
= Fx(F -1x(t)) =
t.
(LT(x))
= Fx(F -1x(t)) =
t.
Переход
от d к d1 напоминает классическое
преобразование, использованное Н.В. Смирновым при изучении непараметрических критериев
согласия и однородности, а именно, преобразование ![]() , переводящее
случайную величину
, переводящее
случайную величину ![]() с непрерывной
функцией распределения F(x) в случайную величину
с непрерывной
функцией распределения F(x) в случайную величину ![]() ,
равномерно распределенную на отрезке [0,1]. Оба рассматриваемых преобразования существенно
упрощают дальнейшие рассмотрения. Преобразование d1= Fx(d) зависит от точки x, что не влияет на дальнейшие
рассуждения, поскольку ограничиваемся изучением сходимости в отдельно взятой точке.
,
равномерно распределенную на отрезке [0,1]. Оба рассматриваемых преобразования существенно
упрощают дальнейшие рассмотрения. Преобразование d1= Fx(d) зависит от точки x, что не влияет на дальнейшие
рассуждения, поскольку ограничиваемся изучением сходимости в отдельно взятой точке.
Функцию d1(x,y), для которой мера шара радиуса t равна t, называем в соответствии с работой [31] «естественным показателем различия» или «естественной метрикой». В случае конечномерного пространства Rk и евклидовой метрики d имеем d1(x,y) = ck d k (x,y), где ck - объем шара единичного радиуса в Rk .
Поскольку можно записать, что
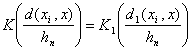 ,
,
где
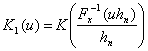 ,
,
то переход от одного показателя различия к другому, т.е. от d к d1 соответствует переходу от одной ядерной функции к другой, т.е. от K к K1. Выгода от такого перехода заключается в том, что утверждения о поведении непараметрических оценок плотности приобретают более простую формулировку.
Теорема 5. Пусть d - естественная метрика, плотность f непрерывна в точке x и ограничена на всем пространстве X , причем f(x)>0, ядерная функция K(u) удовлетворяет простым условиям регулярности
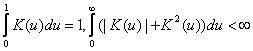 .
.
Тогда
![]() n(hn
,x) = nhn , оценка fn(x) является состоятельной, т.е.
fn(x)
n(hn
,x) = nhn , оценка fn(x) является состоятельной, т.е.
fn(x)![]() f(x) по
вероятности при n
f(x) по
вероятности при n![]() и, кроме
того,
и, кроме
того,
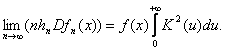
Теорема
5 доказывается методами, развитыми в работе [31]. Однако остается открытым вопрос
о скорости сходимости ядерных оценок, в частности, о поведении величины ![]() n =
M(fn(x)-f(x))2 - среднего квадрата ошибки, и
об оптимальном выборе показателей размытости hn . Для того, чтобы
продвинуться в решении этого вопроса, введем новые понятия. Для случайного элемента
X(
n =
M(fn(x)-f(x))2 - среднего квадрата ошибки, и
об оптимальном выборе показателей размытости hn . Для того, чтобы
продвинуться в решении этого вопроса, введем новые понятия. Для случайного элемента
X(![]() ) со
значениями в X рассмотрим т.н. круговое распределение G(x,t) = P{d(X(
) со
значениями в X рассмотрим т.н. круговое распределение G(x,t) = P{d(X(![]() ), x)<t}
и круговую плотность g(x,t)= G't(x,t).
), x)<t}
и круговую плотность g(x,t)= G't(x,t).![]()
Теорема 6. Пусть ядерная функция K(u) непрерывна и финитна, т.е. существует число E такое, что K(u)=0 при u>E. Пусть круговая плотность является достаточно гладкой, т.е. допускает разложение
![]()
![]()
при некотором k, причем остаточный член равномерно ограничен на [0,hE]. Пусть
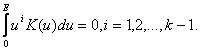
Тогда
![]()
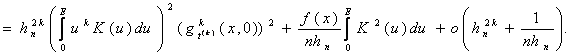
Доказательство
теоремы 6 проводится с помощью разработанной в статистике объектов нечисловой природы
математической техники, образцы которой представлены, в частности, в работе
[31]. Если коэффициенты при основных членах в правой части последней формулы не
равны 0, то величина ![]() n достигает
минимума, равного
n достигает
минимума, равного 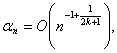 при
при ![]() Эти
выводы совпадают с классическими результатами, полученными ранее рядом авторов для
весьма частного случая прямой X = R1 (см., например, монографию [32, с.316]). Заметим,
что для уменьшения смещения оценки приходится применять знакопеременные ядра K(u).
Эти
выводы совпадают с классическими результатами, полученными ранее рядом авторов для
весьма частного случая прямой X = R1 (см., например, монографию [32, с.316]). Заметим,
что для уменьшения смещения оценки приходится применять знакопеременные ядра K(u).
Непараметрические оценки плотности в конечных пространствах. В случае конечных пространств естественных метрик не существует. Однако можно получить аналоги теорем 5 и 6, переходя к пределу не только по объему выборки n, но и по новому параметру дискретности m.
Рассмотрим
некоторую последовательность Xm , m = 1,2,…- конечных пространств.
Пусть в Xm заданы показатели различия dm . Будем
использовать нормированные считающие меры ![]() ставящие
в соответствие каждому подмножеству А долю элементов всего пространства Xm
, входящих в А. Как и ранее, рассмотрим как функцию t объем
шара радиуса t, т.е.
ставящие
в соответствие каждому подмножеству А долю элементов всего пространства Xm
, входящих в А. Как и ранее, рассмотрим как функцию t объем
шара радиуса t, т.е. ![]() Введем аналог
естественного показателя различия
Введем аналог
естественного показателя различия ![]() Наконец,
рассмотрим аналоги преобразования Смирнова
Наконец,
рассмотрим аналоги преобразования Смирнова ![]() Функции
Функции
![]() , в отличие
от ситуации предыдущего раздела, уже не совпадают тождественно с t, они кусочно-постоянны
и имеют скачки в некоторых точках ti , i =1,2,…, причем в этих точках
, в отличие
от ситуации предыдущего раздела, уже не совпадают тождественно с t, они кусочно-постоянны
и имеют скачки в некоторых точках ti , i =1,2,…, причем в этих точках
![]()
Теорема
7. Пусть точки скачков равномерно сближаются, т.е. ![]() при
при ![]() (другими
словами,
(другими
словами,![]() -t|
-t|![]() при
при ![]() ). Тогда
существует последовательность параметров дискретности mn такая, что при предельном переходе
). Тогда
существует последовательность параметров дискретности mn такая, что при предельном переходе ![]() справедливы заключения теорем 5 и 6.
справедливы заключения теорем 5 и 6.
Пример
1. Пространство ![]() всех подмножеств
конечного множества
всех подмножеств
конечного множества ![]() из m элементов
допускает (см. монографию [3]) аксиоматическое введение метрики
из m элементов
допускает (см. монографию [3]) аксиоматическое введение метрики ![]() где
где ![]() - символ
симметрической разности множеств. Рассмотрим непараметрическую ядерную оценку плотности
типа Парзена - Розенблатта
- символ
симметрической разности множеств. Рассмотрим непараметрическую ядерную оценку плотности
типа Парзена - Розенблатта
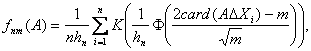
где
![]() - функция
нормального стандартного распределения. Можно показать, что эта оценка удовлетворяет
условиям теоремы 7 с
- функция
нормального стандартного распределения. Можно показать, что эта оценка удовлетворяет
условиям теоремы 7 с ![]()
Пример
2. Рассмотрим пространство функций ![]() определенных
на конечном множестве
определенных
на конечном множестве ![]() , со значениями
в конечном множестве
, со значениями
в конечном множестве ![]() . Это пространство
можно интерпретировать как пространство нечетких множеств (см. о нечетких множествах,
напаример, монографии [3,10]), а именно, Yr -
носитель нечеткого множества, а Zq - множество значений
функции принадлежности. Очевидно, число элементов пространства Xm равно
(q+1)r . Будем использовать
расстояние
. Это пространство
можно интерпретировать как пространство нечетких множеств (см. о нечетких множествах,
напаример, монографии [3,10]), а именно, Yr -
носитель нечеткого множества, а Zq - множество значений
функции принадлежности. Очевидно, число элементов пространства Xm равно
(q+1)r . Будем использовать
расстояние ![]() Непараметрическая
оценка плотности имеет вид:
Непараметрическая
оценка плотности имеет вид:
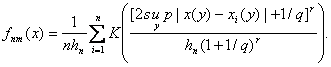
Если
![]() , то при
, то при
![]() >
>![]() выполнены
условия теоремы 7, а потому справедливы теоремы 5 и 6.
выполнены
условия теоремы 7, а потому справедливы теоремы 5 и 6.
Пример
3. Рассматривая пространства ранжировок m объектов, в качестве расстояния
d(A,B) между ранжировками A и B примем
минимальное число инверсий, необходимых для перехода от A к B.
Тогда max(ti -ti-1)
не стремится к 0 при ![]() , условия
теоремы 7 не выполнены.
, условия
теоремы 7 не выполнены.
Пример
4. В прикладных работах наиболее распространенный пример объектов нечисловой
природы – вектор разнотипных данных: реальный объект описывается вектором, часть
координат которого - значения количественных признаков, а часть - качественных
(номинальных и порядковых). Для пространств разнотипных признаков, т.е. декартовых
произведений непрерывных и дискретных пространств, возможны различные постановки.
Пусть, например, число градаций качественных признаков остается постоянным. Тогда
непараметрическая оценка плотности сводится к произведению частоты попадания в точку
в пространстве качественных признаков на классическую оценку Парзена-Розенблатта
в пространстве количественных переменных. В общем случае расстояние d(x,y) можно, например, рассматривать как сумму трех расстояний.
А именно, евклидова расстояния d1 между количественными факторами, расстояния d2 между номинальными признаками (d2(x,y) = 0, если x = y, и d2(x,y) = 1, если ![]() ) и расстояния
d3 между порядковыми переменными (если x и y - номера градаций, то d3(x,y) = |x
- y|). Наличие количественных факторов приводит к непрерывности
и строгому возрастанию функции Fmx(t), а потому для непараметрических
оценок плотности в пространствах разнотипных признаков верны теоремы 5 - 6.
) и расстояния
d3 между порядковыми переменными (если x и y - номера градаций, то d3(x,y) = |x
- y|). Наличие количественных факторов приводит к непрерывности
и строгому возрастанию функции Fmx(t), а потому для непараметрических
оценок плотности в пространствах разнотипных признаков верны теоремы 5 - 6.
Статистика объектов нечисловой природы как часть эконометрики продолжает бурно развиваться. Увеличивается количество ее практически полезных применений при анализе конкретных экономических данных - в маркетинговых исследованиях, контроллинге, при управлении предприятием и др.
|
|