


 |
 |
 |
Следующая программа
вычерчивает в диалоговом окне кривую Гильберта. На рис. 12.7 приведены кривые
Гильберта первого, второго и третьего порядков. Если присмотреться, то видно,
что кривая второго порядка получается путем соединения прямыми линиями четырех
кривых первого порядка. Аналогичным образом получается кривая третьего порядка,
но при этом в качестве "кирпичиков" используются кривые второго порядка.
Таким образом, чтобы нарисовать кривую третьего порядка, надо нарисовать четыре
кривых второго порядка. В свою очередь, чтобы нарисовать кривую второго порядка,
надо нарисовать четыре кривых первого порядка. Таким образом, алгоритм вычерчивания
кривой Гильберта является рекурсивным.
Диалоговое окно программы
Кривая Гильберта, в котором находится кривая пятого порядка, приведено на рис.
12.8, текст программы — в листинге 12.4.
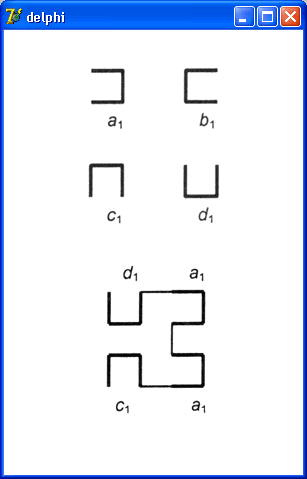
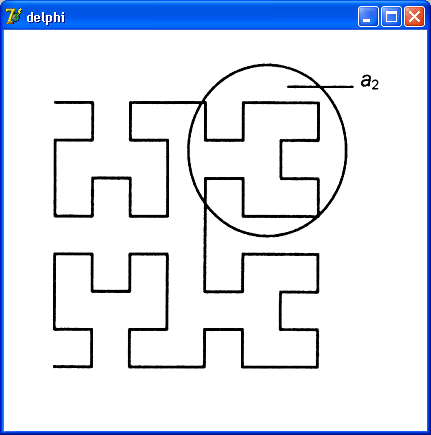
Рис. 12.7. Кривые
Гильберта первого, второго и третьего порядков

Рис. 12.8. Кривая
Гильберта пятого порядка
Листинг 12.4.
Кривая Гильберта
unit
gilbert_;
interface
uses
Windows, Messages, SysUtils,
Variants, Classes, Graphics,
Controls,
Forms, Dialogs, StdCtrls, ComCtrls;
type
TForml
= class(TForm)
procedure FormPaint(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1:
TForm1;
implementation
{$R *.dfm}
var
p: integer =5; // порядок кривой
u:
integer =7; // длина штриха
{ Кривую Гильберта можно получить путем
соединения
элементов а,b,с и d.
Каждый элемент строит
соответствующая процедура. }
procedure a(i:integer; canvas: TCanvas); forward;
procedure b(i:integer; canvas: TCanvas); forward;
procedure с(i:integer; canvas: TCanvas); forward;
procedure
d(i:integer; canvas: TCanvas); forward;
//
Элементы кривой
procedure a(i: integer; canvas: TCanvas);
begin
if
i > 0 then begin
d(i-l, canvas);
canvas.LineTo(canvas.PenPos.X+u,canvas.PenPos.Y);
a(i-l, canvas);
canvas.LineTo(canvas.PenPos.X,canvas.PenPos.Y+u);
a(i-l, canvas);
canvas.LineTo(canvas.PenPos.X-u,canvas.PenPos.Y);
с (i-1, canvas);
end;
end;
procedure
b(i: integer; canvas: TCanvas);
begin
if
i > 0 then begin
c(i-l, canvas);
canvas.LineTo(canvas.PenPos.X-u,canvas.PenPos.Y);
b(i-1, canvas);
canvas.LineTo(canvas.PenPos.X,canvas.PenPos.Y-u);
b(i-l, canvas);
canvas.LineTo(canvas.PenPos.X+u, canvas.PenPos.Y);
d(i-l, canvas);
end;
end;
procedure c(i: integer; canvas: TCanvas);
begin
if
i > 0 then begin
b(i-1, canvas);
canvas.LineTo(canvas.PenPos.X,canvas.PenPos.Y-u);
с (i-1, canvas);
canvas.LineTo(canvas.PenPos.X-u,canvas.PenPos.Y);
c(i-1, canvas);
canvas.LineTo(canvas.PenPos.X,canvas.PenPos.Y+u);
a(i-1, canvas);
end;
end;
procedure d(i: integer; canvas: TCanvas);
begin
if
i > 0 then begin
a(i-1, canvas);
canvas.LineTo(canvas.PenPos.X,canvas.PenPos.Y+u);
d(i-1, canvas);
canvas.LineTo(canvas.PenPos.X+u,canvas.PenPos. Y) ;
d(i-1, canvas);
canvas.LineTo(canvas.PenPos.X,canvas.PenPos.Y-u);
b(i-1, canvas);
end;
end;
procedure TForml.FormPaint(Sender: TObject);
begin
Form1.Canvas.MoveTo(u,
u) ;
a(5,Form1.Canvas); // вычертить кривую Гильберта
end;
end.
Следует обратить внимание на следующую особенность реализации программы. Процедура, которая вычерчивает элемент а, помимо самой себя (для вычерчивания элемента а кривой более низкого порядка) вызывает процедуры d и ь, описание (текст) которых в тексте программы находится после процедуры а. Чтобы компилятор не вывел сообщение об ошибке, в текст программы помещено объявление процедуры с ключевым словом forward, означающим, что это только объявление, а описание (реализация) находится дальше. Таким образом, уже в процессе компиляции процедуры а, компилятор "знает", что имена ь и d означают процедуры.
 |
 |
 |
|
|