Процессоры электронных таблиц. Решение уравнений и оптимизационных задач

Широкое применение на практике находят функции и режимы Excel, предназначенные для поиска решения уравнений и оптимизационных задач.

Подбор параметра
Удобным и простым для понимания инструментом решения уравнений является режим Подбор параметра. Он реализует алгоритм численного решения уравнения, зависящего от одной или нескольких переменных.
Процесс решения с помощью данного метода распадается на два этапа:
1. Задание на рабочем листе ячеек, содержащих переменные решаемого уравнения (так называемых влияющих ячеек), и ячейки, содержащей формулу уравнения (зависимой или целевой ячейки).
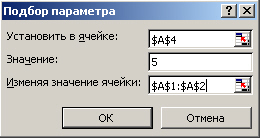
2. Ввод адресов влияющих и целевой ячеек в диалоговое окно Подбор параметра и получение ответа (или сообщения о его отсутствии/невозможности найти).
Рассмотрим теперь применение режима Подбор параметра на ряде конкретных примеров.
Пример 1. Найти решение уравнения Зх2-2у2=5.
Результат создания влияющих и целевых ячеек показан на рис. 6.31, а ввод параметров в окно диалога, появляющегося при выполнении команды меню Сервис > Подбор параметра..., - на рис. 6.32.

Наконец, на рис. 6.33 показан результат выполнения процедуры подбора параметра.

По видимому в результирующее окно (рис. 6.33) Текущему значению можно судить о степени точности найденного результата. Если нажать кнопу ОК, то содержимое влияющих ячеек (в нашем случае это ячейки А1 и А2) будет заменено на решения уравнения. Дополнительно отметим, что поскольку рассматриваемое уравнение Зх2-2у2=5 зависит от двух переменных и имеет бесконечное множество решений, то какие числа мы получим в ячейках А1 и А2, непосредственно зависит от их исходного содержания (так называемого начального приближения).
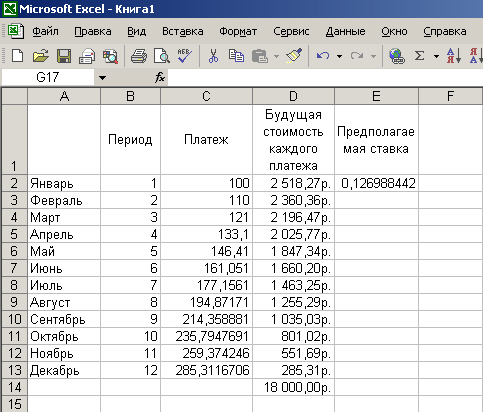
Пример 2. Определить, при какой ежемесячной процентной ставке можно за год накопить 5 тыс. р., внося каждый месяц платеж на 10% больше предыдущего, начав с первого платежа 100 р.
С помощью одной лишь финансовой функций эту задачу решить нельзя, в ней слишком много неизвестных. Для начала необходимо смоделировать реальный поток платежей, затем найти накопленную к концу года сумму, нарастив каждый платеж по предполагаемой ставке (так как в задаче дана ежемесячная ставка) на соответствующее число процентных периодов (первый платеж на 12 месяцев вперед, второй - на 11 и т. п., см. рис. 6. 35), и только после этого с помощью Подбора параметра найти истинное значение процентной ставки. Ответ: 12,70%, см. рис. 6.36.

Очевидно, что "платой" за простоту такого инструмента, как Подбор параметра, является ограниченность его возможностей. Еще раз подчеркнем, что с его помощью могут быть решены только отдельно взятые уравнения.

Применение надстройки Поиск решения
Значительно более мощным по сравнению с Подбором параметра средством решения уравнения, а также достаточно эффективным инструментом решения оптимизационных задач является программная надстройка Поиск решения. Напомним, что вопросы установки надстроек были рассмотрены ранее в 6.2.2 в связи с надстройкой Пакет анализа. В случае успешной установки программной надстройки Поиск решения в меню Сервис появляется дополнительный пункт Поиск решения.... Рассмотрим процесс ее использования на примере простейшей задачи об управлении портфелем активов.
Пусть перед некоторым инвестором стоит проблема принятия решения о вложении имеющегося у него капитала. Набор характеристик потенциальных объектов для инвестирования, имеющих условные имена от А до F, задается в табл. 6.6.
Предположим, что при принятии решения о приобретении активов должны быть соблюдены условия:
1. Суммарный объем капитала, который должен быть вложен, составляет $100000.
2. Доля средств, вложенная в один объект, не может превышать четверти от всего объема.

3. Более половины всех средств должны быть вложены в долгосрочные активы (допустим, на рассматриваемый момент к таковым относятся активы со сроком погашения после 2004 года).
4. Доля активов, имеющих надежность менее чем 4 балла, не может превышать трети от суммарного объема.
Дадим теперь описание экономико-математической модели для данной ситуации. В рассматриваемом примере в качестве управляемых переменных выступают объемы средств, вложенных в активы той или иной фирмы. Обозначим их как XA, XB , Xс XD, XE, XF. Тогда суммарная прибыль от размещенных активов, которую получит инвестор, может быть представлена в виде

На следующем этапе моделирования мы должны формально описать перечисленные выше ограничения 1 - 4 на структуру портфеля.
1. Ограничение на суммарный объем активов:

2. Ограничение на размер доли каждого актива:

3. Ограничение, связанное с необходимостью вкладывать половину средств в долгосрочные активы:

Наконец, система ограничений в соответствии с экономическим смыслом задачи должна быть дополнена условиями неотрицательности для искомых переменных:
xA ? 0, xB ? 0, xC ? 0, xD ? 0, xE ? 0, xF ? 0.

Перечисленные условия образуют математическую модель поведения инвестора. В рамках этой модели может быть поставлена задача поиска таких значений переменных xA, xB , xC , xD, xE, xF,
при которых достигается наибольшее значение прибыли и одновременно выполняются ограничения на структуру портфеля активов.
Перейдем к решению сформулированной задачи с помощью инструментов, предоставляемых программным обеспечением MS Excel. Оно распадается на следующие Шаги:
1 . На выбранном рабочем листе задать ячейки, которые будут предназначены для ссохранения переменных решаемой задачи (xA, xB , xC , xD, xE, xF,), как это сделано на рис. 6.37, где переменная xA содержится в ячейке А2, xB - в В2 и т. д. Заметим чтo хорошим стилем работы является использование смежных ячеек для хранения имён переменных (на рис. 6.37 для этого служат ячейки с Al no F1). Очевидно, что ни в коем случае не следует путать ячейки с переменными с ячейками со смысловыми именами. Увы, у начинающих пользователей это весьма распространенная ошибка.
2. Задать ячейку, содержащую формулу целевой функции решаемой задачи. В нашем примере ячейка Н2 содержит формулу
=0, 055 * А2 + 0, 06 * B2 + 0, 08 * С2 + 0, 075 * D2 + 0, 055 * Е2 + 0, 07 * F2.

3. Заполнить ячейки для формул "сложных" ограничений (типа xB + xC ? 50000. и т. п.). На рис. 6.37 для этого использованы ячейки D4, D5, D6, а ячейки А4, А5, А6 содержат соответствующие подписи.

ПРИМЕЧАНИЕ
Интерфейс надстройки Поиск решения устроен таким образом, что непосредственно в режиме диалога могут вводиться только ограничения типа А2 <= 25 000 или А2 >= 0. Поэтому для учета условия вида xB + xC ? 50000 нужно в некоторую вспомогательную ячейку ввести формулу с левой частью неравенства и уже для нее задать ограничение >= 50 000.

4. Выполнить команду меню Сервис > Поиск решения....
5. Заполнить параметры диалогового окна Поиск решения: адрес ячейки целевой функции (целевой ячейки), тип оптимизации (искать максимум или минимум), адреса ячеек с переменными.
6. Задать систему ограничений, для чего используется кнопка Добавить (группа Ограничения). По ее нажатию вызывается вспомогательное диалоговое окно в поля которого вводятся адреса или значения, образующие выражение для условия, накладываемого на переменные решаемой задачи. Как видно, сформированную систему ограничений в дальнейшем можно редактировать. Для этого служат кнопки Изменить и Удалить.
7. Нажать кнопку Выполнить, после чего будет осуществлена процедура поиска решения, по результатам которой выводится сообщение о найденном решении (или о невозможности его обнаружить). Как видно из данного рисунка, полученные результаты можно сохранить (кнопка ОК), изменив, таким образом, содержимое ячеек с переменными, можно от них отказаться (не сохранять), наконец, можно сформировать отчет с более подробной информацией о том, как проходил процесс поиска решения. Таким образом, мы получили, что при оптимальном распределении прибыль инвестора составит $6374,4.

ПРИМЕЧАНИЕ

Как уже отмечалось ранее, сходимость (нахождение решения за конечное число шагов) в численных алгоритмах оптимизации не гарантируется. Однако в случае, если решение не найдено, пользователь, обладающий некоторой математической подготовкой, может оказать определенное влияние на процесс поиска, изменив значения его параметров, которые установлены по умолчанию (см. рис. 6.38, кнопка Параметры). В некоторых случаях такие вариации могут привести к положительному результату.
Другой полезный совет, который можно дать в случае, когда решение не удается найти сразу, касается изменения начальных значений переменных. Последнее оказывается полезным и с точки зрения анализа найденного решения на устойчивость (независимость от того, с какой точки начинается его поиск).

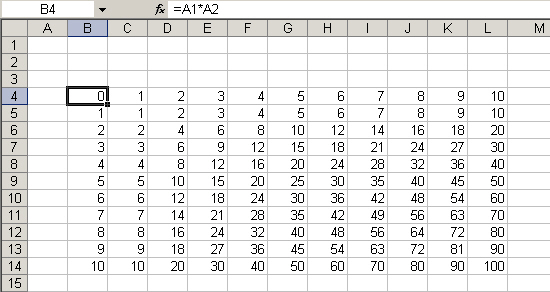
Пример расчетов с использованием Таблиц подстановки

Зачастую при проведений финансово-экономических расчетов возникает необходимость провести вычисления по одним и тем же формулам, но для различных серий данных. Конечно, с данной проблемой можно справиться с помощью простого копирования формул, однако в Excel предусмотрен и более удобный способ ее решения с помощью так называемой таблицы подстановки. Ее идея состоит в связывании некоторой формулы с сериями значений, которые должны быть подставлены вместо некоторых переменных, входящих в данную формулу. Таблицы подстановки в Excel могут содержать одну или две подстановочных переменных, или, другими словами, быть векторными или матричными. Применение таблицы подстановки с двумя переменными продемонстрируем на простом, но наглядном примере - для построения таблицы умножения. Серия подстановочных значений по строкам

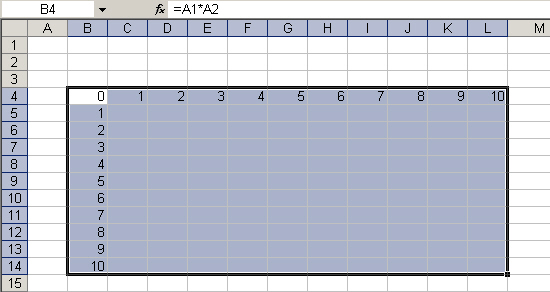
Необходимо проделать следующие операции:
1. Определить две ячейки, содержащие переменные. В нашем случае (рис. 6.42) это ячейки А1 и А2. Начальное содержимое данных ячеек может быть произвольным, так как они нужны для того, чтобы определить переменные, от которых будет зависеть целевая формула.
2. Задать в "матричной" форме, как это показано на рис. 6.42, целевую формулу, зависящую от ячеек, определенных на этапе 1 (для нашего примера - это формула ~А1*А2), а также серии значений, предназначенных для подстановки вместо переменных. Серии значений должны располагаться в левой колонке и верхней строке. При определении таблицы необходимо соблюдать очевидное правило - ячейки с переменными не должны попасть в ее внутреннюю область.
3. Выделить область таблицы, как это показано на рис. 6.42.
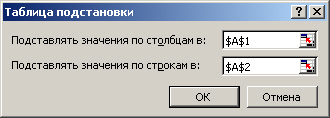
4. Выполнить команду меню Данные > Таблица подстановки....
5. Заполнить параметры в появившемся диалоговом окне (рис. 6.43). Первое значение - Подставлять значения по столбцам в - задает адрес ячейки с той переменной, вместо которой в целевую формулу будут подставляться значения из крайней верхней строки таблицы подстановки. В нашем случае вместо переменной из ячейки А1 последовательно будут подставлены в формулу значения из интервала C4:L4. Аналогично, второе значение - Подставлять значения по строкам в - задает адрес ячейки той переменной, вместо которой в целевую формулу будут подставляться значения из крайнего левого столбца таблицы подстановки. В нашем примере вместо переменной из ячейки А2 в формулу будут подставлены значения из интервала В5:В14.
6. Нажать кнопку ОК.

Результат заполнения таблицы подстановки показан на рис. 6.44.

Знаете ли Вы, что низкочастотные электромагнитные волны частотой менее 100 КГц коренным образом отличаются от более высоких частот падением скорости электромагнитных волн пропорционально корню квадратному их частоты от 300 тысяч кмилометров в секунду при 100 кГц до примерно 7 тыс км/с при 50 Гц.

Название	Доходность, в %	Срок выкупа, год	Надежность, баллы
А	5,5	2001	5
B	6,0	2005	4
C	8,0	2010	2
D	7,5	2002	3
E	5,5	2000	5
F	7,0	2003	4