 5GL
5GL
 5GL
5GL
|
Таблица ПЗ.1. Арифметические операторы
| Оператор |
Клавиши |
Скаляр |
Вектор |
Матрица |
| := |
<:> |
Присваивание |
||
| = |
<~> |
Глобальное присваивание |
||
| = |
<=> |
Численный вывод |
||
| - |
<Ctrl>+<=> |
Символьный вывод |
||
| + |
<+> |
Сложение |
||
| - |
<-> |
Вычитание или отрицание (унарная операция) |
||
| <*> |
Умножение |
Матричное умножение, умножение на скаляр |
||
| Скалярное произведение |
||||
| x |
<Ctrl>+<8> |
Деление |
||
| / |
</> либо <Ctrl>+</> |
Факториал |
||
| ! |
<!> |
|||
| - |
<"> |
Комплексное сопряжение |
||
|
|
<\> |
Квадратный корень |
||
 |
<Ctrl>+<\> |
Корень n-й степени |
||
 |
<'> |
Скобки (изменение приоритета) |
||
 |
<[> |
Нижний индекс |
||
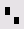 |
<Ctrl>+<1> |
Транспонирование |
||
 |
<Shift>+<\> |
Модуль |
Модуль вектора |
Определитель |
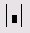 |
<Ctrl>+<4> |
Сумма элементов |
||
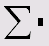 |
Обратная величина |
Обратная матрица |
||
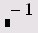 |
<л>+п |
Возведение в степень n |
Возведение матрицы в степень n |
|
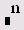 |
<Ctrl>+<-> |
Векторизация |
||
 |
<Ctrl>+<6> |
Выделение столбца |
||
Скалярные операции над векторами и матрицами, если это не оговорено особо, производятся независимо над их каждым элементом, как над скаляром.
Таблица П3.2. Вычислительные операторы
|
Оператор |
Клавиши |
Описание |
Ссылка |
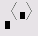 |
<Shift>+<7> |
Определенный интеграл |
7.1 |
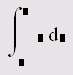 |
<Ctrl>+<!> |
Неопределенный интеграл |
7.1.3 |
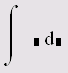 |
<?> |
Дифференцирование |
7.2 |
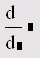 |
<Ctrl>+<?> |
Вычисление n-й производной |
7.2 |
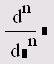 |
<Ctrl>+<Shift >+<4> |
Сумма |
3.2.2 |
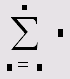 |
<Ctrl>+<4> |
Сумма ранжированной переменной |
3.2.2 |
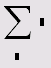 |
<Ctrl>+<Shift >+<3> |
Произведение |
3.2.2 |
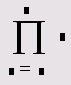 |
<Ctrl>+<3> |
Произведение ранжированной переменной |
3.2.2 |
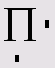 |
<Ctrl>+<L> |
Предел |
3.2.2 |
 |
<Ctrl>+<A> |
Левый предел |
3.2.2 |
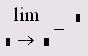 |
<Ctrl>+<B> |
Правый предел |
3.2.2 |
Таблица ПЗ.З. Встроенные функции по алфавиту
| Оператор |
Клавиши |
Описание |
Ссылка |
| a*(z) |
z — аргумент |
Обратная тригонометрическая или гиперболическая функция * |
10.4-5 |
| Ai(x) |
х — аргумент |
Функция Эйри первого рода |
15.1.3 |
| angle (x, у) |
х,у — координаты точки |
Угол между точкой и осью ОХ |
10.4 |
| APPENDPRN(file) |
file— строковое представление пути к файлу |
Дозапись данных в существующий текстовый файл |
16.6.1 |
| arg(z) |
z — аргумент функции |
Аргумент комплексного числа |
10.2 |
| atan2 (x,y) |
х,у — координаты точки |
Угол, отсчитываемый от оси ОХ до точки (х,у) |
10.4 |
| Augment (A, B, C, ...) |
А,В,С,... — векторы или матрицы |
Слияние матриц слева направо |
9.2.2 |
| bei (n,x) ber (n, x) |
n — порядок х — аргумент |
Мнимая и действительная части функции Бесселя —Кельвина |
15.1.4 |
| Bi(x) |
х — аргумент |
Функция Эйри второго рода |
15.1.3 |
| bspline (x,y,u, n) |
х,у — векторы данных и — вектор значений сшивок В-сплайнов n — порядок полиномов |
Вектор коэффициентов В-сплайна |
15.1.3 |
| Bulstoer (y0, t0, t1, M, D) |
См. rkf ixed |
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера |
11.3 |
| bulstoer (y0, t0, t1, acc, D, k, s) |
См. rkadapt |
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера (для определения только последней точки интервала) |
11.3 |
| Bvalf it (z1, z2, x0, x1, xf, D, load1, load2, score) |
zl,z2 — вектор начальных значений для недостающих левых и правых граничных условий хО — левая граница xl — правая граница xf — внутренняя точка D(x,y) — векторная функция, задающая систему ОДУ |
Возвращает вектор недостающих граничных условий у краевой задачи для системы N ОДУ с дополнительным условием в промежуточной точке |
12.1.4 |
| loadl (xO , z ) , Ioad2 (xl , z ) -векторные функции, задающие левые и правые граничные условия score (xf , у ) — векторная функция, задающая сшивку решений в xf |
|||
| ceil(x) |
х — аргумент |
Наименьшее целое, не меньшее х |
10.8 |
| cfft(y) CFFT(y) |
у — вектор данных |
Вектор прямого комплексного преобразования Фурье (в разных нормировках) |
15.4.1 |
| cholesky (A) |
А — квадратная, определенная матрица |
Разложение Холецкого |
95.1 |
| cols (A) |
А — матрица или вектор |
Число столбцов |
9.2.3 |
| concat (S1, 32, ...) |
SI, S2,... —строки |
Объединение строковых переменных |
10.7 |
| cond1 (A) cond2 (A) conde(A) condi (A) |
А — квадратная матрица |
Числа обусловленности в разных нормах (Ы, L2, Евклидова, ») |
926 |
| cos (z) |
z — аргумент |
Косинус |
10.4 |
| cosh(z) |
z — аргумент |
Гиперболический косинус |
10.5 |
| cot(z) |
z — аргумент |
Котангенс |
10.4 |
| coth(z) |
z — аргумент |
Гиперболический котангенс |
10.5 |
| csort (A, i) |
А — матрица i — индекс столбца |
Сортировка строк матрицы по элементам 1-го столбца |
9.2.4 |
| CreateMesh (F, s0, s1, t0, t1, sgr, tgr, fmap) |
F ( s , t ) — векторная функция из трех элементов tO.tl — пределы! sO.sl — пределы s tgr, sgr — число точек сетки по t и s fmap— функция преобразования координат |
Создание вложенного массива, представляющего х-, у- и z -координаты параметрической поверхности, заданной функцией F |
9.2.1 |
| Cre-ateSpace(F[, t0, t1, tgr, fmap]) |
F(t) — векторная функция из трех элементов to.tl — пределы t tgr — число точек сетки по t fmap— функция преобразования координат |
Создание вложенного массива, представляющего х-, у- и z -координаты параметрической пространственной кривой, заданной функцией F |
9.2.1 |
| csc (z) |
z — аргумент |
Косеканс |
10.4 |
| csch(z) |
z — аргумент |
Гиперболический косеканс |
10.5 |
| csgn (z) |
z — аргумент |
Комплексный знак числа |
10.2 |
| cspline (x,y) |
х,у — векторы данных |
Вектор коэффициентов кубического сплайна |
15.1.2 |
| cyl2xyz (r, O, z) |
r,6,z— цилиндрические координаты |
Преобразование цилиндрических координат в прямоугольные |
10.10 |
| D* (x,par) |
х— значение случайной величины par — список параметров распределения * |
Плотность вероятности со статистикой распределения * |
14.1.4 |
| diag(v) |
v — вектор |
Диагональная матрица, на диагонали которой находятся элементы вектора |
9.2.1 |
| eigenvals (A) |
А — квадратная матрица |
Собственные значения матрицы |
9.4 |
| eigenvec (A, A,) |
А — квадратная матрица А. — собственное значение |
Собственный вектор матрицы, соответствующий заданному собственному значению |
94 |
| eigenvecs (A) |
А — квадратная матрица |
Собственные векторы матрицы |
9.4 |
| erf (x) |
х — аргумент |
Функция ошибок |
14.1.1 |
| erfc(x) |
х — аргумент |
Обратная функция ошибок |
14.1.1 |
| error (S) |
S — строка |
Возвращает строку S как сообщение об ошибке |
10.7 |
| exp(z) |
z — аргумент |
Экспонента в степени z |
10.3 |
| expf it(x,y,g) |
x,y — векторы данных g — вектор начальных значений а,Ь,с |
Регрессия экспонентой a-ebx+c |
15.2.3 |
| fft(y) FFT(y) |
у — вектор данных |
Вектор прямого преобразования Фурье (в разных нормировках) |
15.4.1 |
| fhyper (a,b,c,x) |
а,Ь,с — параметры х — аргумент, -1<х<1 |
Гауссова гипергеометрическая функция |
10.6 |
| Find (xl,x2, . . . ) |
х!,х2,... — переменные |
Возвращает корень алгебраического уравнения (скаляр) или системы (вектор), определенных в блоке с Given |
8.3-8.4 |
| floor (x) |
х — аргумент |
Наибольшее целое число, меньшее или равное х |
10.8 |
| Gamma ( x ) Gamma ( a , x ) |
х — аргумент |
Гамма-функция Эйлера или неполная гамма-функция порядка а |
10.6 |
| genf it (x,y,g,G) |
х,у — векторы данных g — вектор начальных значений параметров регрессии G ( х , С ) — векторная функция, составленная из функции пользователя и ее частных производных по каждому параметру |
Вектор коэффициентов регрессии функциями пользователя общего вида |
15.2.4 |
| geninv(A) |
А — матрица |
Создание обратной матрицы |
9.2.1 |
| genvals (A,B) |
А, в — квадратные матрицы |
Расчет обобщенных собственных значений |
9.4 |
| genvecs (A,B) |
А, в — квадратные матрицы |
Расчет обобщенных собственных векторов |
9.4 |
| Given |
Ключевое слово для ввода систем уравнений, неравенств и т. п. |
8.3 |
|
| heaviside step(x) |
x — аргумент |
Функция Хевисайда |
10.9 |
| Her (n,x) |
x — аргумент n — порядок |
Полином Эрмита |
10.6 |
| I0(x) I1(x) In (m, x) |
x — аргумент |
Модифицированная функция Бесселя первого рода нулевого, первого и т-го порядка |
10.1.2 |
| ibeta (a, x,y) |
х,у — аргументы а — параметр |
Неполная бета-функция |
10.6 |
| identity (N) |
N — размер матрицы |
Создание единичной матрицы |
9.2.1 |
| icfft (v) ICFFT(v) |
v — вектор частотных данных Фурье-спектра |
Вектор комплексного обратного преобразования Фурье (в разных нормировках) |
15.4.1 |
| if (cond, x,y) |
cond — логическое условие х,у — значения, возвращаемые, если условие верно (ложно) |
Функция условия |
10.9 |
| ifft(v) IFFT(v) |
v — вектор частотных данных Фурье-спектра |
Вектор обратного преобразования Фурье (в разных нормировках) |
15.4.1 |
| IsString(x) |
х — аргумент |
Возвращает 1, если х — строка, и 0 в остальных случаях |
10.7 |
| iwave (v) |
v — вектор частотных данных вейвлет-спектра |
Вектор обратного вейв-лет-преобразования |
15.4.2 |
| lm(z) |
z — аргумент |
Мнимая часть комплексного числа |
10.2 |
| interp (s, x,y, t) |
s — вектор вторых производных х,у — векторы данных t — аргумент |
Сплайн-интерполяция |
15.1.2 |
| intercept (x, у ) |
х,у — векторы данных |
Коэффициент Ь линейной регрессии Ь+а-х |
15.2.1 |
| J0(x) J1(x) Jn (m,x) |
x — аргумент |
Функция Бесселя первого рода нулевого, первого и m-го порядка |
101 1 |
| Jac (n, a,b,x) |
x — аргумент a,b — параметры n — порядок |
Полином Якоби |
106 |
| Is (n,x) |
n — порядок x — аргумент |
Сферическая функция Бесселя первого рода |
101 5 |
| K0(x) K1(x) Kn (m,x) |
x — аргумент |
Модифицированная функция Бесселя второго рода нулевого, первого и m-го порядка |
101 2 |
| Kronecker delta(x,y) |
х,у — аргументы |
Дельта-символ Кроне-кера |
109 |
| ksmooth (x, у , b) |
х,у — векторы данных Ь— ширина окна сглаживания |
Сглаживание с помощью функции Гаусса |
1531 |
| Lag (n, x) |
х — аргумент n — порядок |
Полином Лагерра |
106 |
| last (v) |
v — вектор |
Индекс последнего элемента вектора |
923 |
| Leg (n, x) |
х — аргумент n — порядок |
Полином Лежандра |
106 |
| length (v) |
v — вектор |
Число элементов вектора |
923 |
| line (x, y) |
х,у — векторы данных |
Вектор из коэффициентов линейной регрессии b+a x |
1521 |
| linf it (x,y, F) |
х,у — векторы данных F(x) — векторная функция пользователя |
Вектор коэффициентов регрессии функцией пользователя |
1524 |
| linterp (x, y, t) |
х,у — векторы данных t — аргумент |
Кусочно-линейная интерполяция |
151 1 |
| Igsf it (x,y,g) |
х,у — векторы данных g — вектор начальных значений а,Ь,с |
Регрессия логистической функцией а/ ( 1+Ь е-сх) |
1523 |
| ln(z) |
z — аргумент |
Натуральный логарифм |
10.3 |
| Infit (x,y) |
x,y — векторы данных |
Регрессия логарифмической функцией a-ln(x) +b |
15.2.3 |
| loess (x, у, span) |
x,y — векторы данных span — параметр размера полиномов |
Вектор коэффициентов для регрессии отрезками полиномов (применяется вместе с interp) |
15.2.2 |
| log(z) |
z — аргумент |
Десятичный логарифм |
10.3 |
| log(z, b) |
z — аргумент |
Логарифм z по основанию b |
10.3 |
| logfit (x,y,g) |
х,у — векторы данных g — вектор начальных значений а,Ь,с |
Регрессия логарифмической функцией а-ln (х+b) +с |
15.2.3 |
| Isolve (A,b) |
А — матрица СЛАУ b — вектор правых частей |
Решение системы линейных уравнений (СЛАУ) |
9.3 |
| Ispline (x,y) |
х,у — векторы данных |
Вектор коэффициентов линейного сплайна |
15.1.2 |
| lu(A) |
А — квадратная матрица |
Ш-разложение |
9.5.3 |
| matrix(M, N, f ) |
М — количество строк N — количество столбцов f ( i , j ) — функция |
Создание матрицы с элементами f(i,j) |
9.2.1 |
| Maximize (f, x1 ...) |
f (x1, . . . ) — функция x1, ... — аргументы, по которым производится максимизация |
Вектор значений аргументов, при которых функция f достигает максимума (возможно задание дополнительных условий в блоке с Given) |
8.6 |
| mhyper (a,b,x) |
х — аргумент а, b — параметры |
Конфлюэнтная гипергеометрическая функция |
10.6 |
| Minerr (x1, x2, ...) |
x1,x2,... — переменные |
Возвращает вектор приближенного решения системы уравнений и неравенств, определенных в блоке с Given |
8.5 |
| Minimize (f, x1, ...) |
f ( x1 ,...)— функция x1,... — аргументы, по которым производится минимизация |
Вектор значений аргументов, при которых функция f достигает минимума (возможно задание дополнительных условий в блоке с Given) |
8.6 |
| medsmooth (у, b) |
у — вектор данных b — ширина окна сглаживания |
Сглаживание методом "бегущих медиан" |
15.3.1 |
| Multigrid (F,ncycle) |
F — матрица правой части уравнения Пуассона ncycle — параметр алгоритма (2) |
Матрица решения уравнения Пуассона на квадратной области с нулевыми граничными условиями |
12.4.1 |
| n* (M,par) |
М — размерность вектора х— значение случайной величины par — список параметров распределения * |
Вектор случайных чисел со статистикой * |
14.1.4 |
| norml (A) norm2 (A) norme (A) normi (A) |
А — квадратная матрица |
Нормы матриц (Ы, L2, Евклидова, °°) |
9.2.5 |
| num2str (z) |
z — число |
Возвращает строку, чьи знаки соответствуют десятичному значению числа z |
10.7 |
| Odesolve (t,t1[,step]) |
t — переменная интегрирования ОДУ t1 — конечная точка интервала интегрирования step— число шагов интегрирования ОДУ |
Возвращает матрицу с решением задачи Коши для одного ОДУ, определенного в блоке с Given и начальными условиями в точке Ю |
11.1.1, 11.2 |
| р* (х,раг) |
x— значение случайной величины par — список параметров распределения * |
Функция распределения со статистикой * |
14.1.4 |
| pdesolve(u, x, xrange, t, trange, [xpts] , [tpts])} |
и — вектор имен функций х —пространственная переменная xrange — интервал интегрирования по пространству t — временная переменная trange — интервал интегрирования по времени xpts — число пространственных узлов сетки tpts — число временных шагов сетки |
Возвращает скалярную функцию двух аргументов (x,t), являющуюся решением дифференциального уравнения (или системы уравнений) в частных производных |
13.3.1 |
| pol2xy(r,O) |
r, O — полярные координаты |
Преобразование полярных координат в прямоугольные |
10.10 |
| polyroots (v) |
v — вектор, составленный из коэффициентов полинома |
Возвращает вектор всех корней полинома |
8.2 |
| predict (y, m, n) |
у — исходный вектор т— число элементов у, по которым строится экстраполяция n — количество предсказываемых элементов |
Функция предсказания, экстраполирующая вектор |
15.1.4 |
| pspline(x, y) |
х,у — векторы данных |
Вектор коэффициентов квадратичного сплайна |
15.1.2 |
| pwf it(x, y, g) |
х,у — векторы данных g — вектор начальных значений а,Ь,с |
Регрессия степенной функцией a-xb+c |
15.2.3 |
| q* (p, par) |
р — значение вероятности par — список параметров распределения * |
Квантиль (функция, обратная функции распределения) со статистикой * |
14.1.4 |
| qr(A) |
A — вектор или матрица |
QR-разложение |
9.5.2 |
| Radau (y0, t0, t1, M, D) |
См. rkf ixed |
Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом RADAUS |
11 52 |
| Radau (y0, t0, t1, M, D) |
См. rkf ixed |
Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом RADAUS (для определения только последней точки интервала) |
11.5.2 |
| rank (A) |
A — матрица |
Ранг матрицы |
9.2.7 |
| Re(z) |
z — аргумент |
Действительная часть комплексного числа |
10.2 |
| READ* (file) |
file— строковое представление пути к файлу |
Запись данных в файл типа * |
15.6 |
| regress (x, y, k) |
х,у — векторы данных k — степень полинома |
Вектор коэффициентов для полиномиальной регрессии (применяется вместе с interp) |
15.2.2 |
| Relax (a ,b, c, d, e, F, v, rjac) |
a,b,c,d,e— матрицы коэффициентов разностной схемы F — матрица правой части уравнения v — матрица граничных условий rjac— параметр алгоритма (0...1) |
Матрица решения методом сеток дифференциального уравнения в частных производных на квадратной области |
12.4 1, 12.4.3 |
| reverse (v) |
v — вектор |
Перестановка элементов вектора в обратном порядке |
9.2.4 |
| Rkadapt (y0, t0, t1, acc, D, k, s) |
у0 — вектор начальных условий (t0.t1)— интервал интегрирования асе — погрешность вычисления D ( t , у ) — векторная функция, задающая систему ОДУ k — максимальное число шагов интегрирования s — минимальный шаг интегрирования |
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Рунге-Кутты с переменным шагом и заданной точностью (для определения только последней точки интервала) |
11.3 |
| Rkadapt (у0, t0, t1, M, D) |
См. rkf ixed |
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Рунге-Кутты с переменным шагом |
11.3 |
| rkf ixed (y0, t0, t1, M, D) |
у0 — вектор начальных условий (t0.t1) — интервал интегрирования М — число шагов интегрирования D(t,y) — векторная функция, задающая систему ОДУ |
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Рунге-Кутты с фиксированным шагом |
11.1.2, 11.3 |
| root (f(x,...),x[a,b]) |
f (х, . . . ) —функция х — переменная (а,Ь) — интервал поиска корня |
Возвращает корень функции |
8.1 |
| round ( x , n ) |
х — аргумент n — число знаков округления после десятичной точки |
Округление |
10.8 |
| rows (A) |
А — матрица или вектор |
Число строк |
9.2.3 |
| rref (A) |
А — матрица или вектор |
Преобразование матрицы в ступенчатый вид |
9.2.1 |
| rsort (A, i) |
А — матрица i — индекс строки |
Сортировка матрицы по элементам i -и строки |
9.2.4 |
| sbval (z, x0, x1, D, load, score) |
z — вектор начальных приближений для недостающих начальных условий х0 — левая граница x1 — правая граница D(x,y) — векторная функция, задающая систему ОДУ load(xO,z)— векторная функция с начальными условиями score(xl,y)— векторная функция, задающая правые граничные условия |
Возвращает вектор недостающих начальных условий для двухточечной краевой задачи для системы ОДУ |
12.1.3 |
| search (S, Subs.m) |
S — строка Sub — подстрока m — стартовая позиция поиска |
Стартовая позиция подстроки в строке |
10.7 |
| sec (z) |
z — аргумент |
Секанс |
10.4 |
| sech(z) |
z — аргумент |
Гиперболический секанс |
10.5 |
| sign(x) |
х — аргумент |
Знак числа |
10.9 |
| signum(z) |
z — аргумент |
Комплексный знак числа Z/ | Z | |
10.2 |
| sin(z) |
z — аргумент |
Синус |
10.4 |
| sinh (z) |
z — аргумент |
Гиперболический синус |
10.5 |
| sinf it (x, y, g) |
х,у — векторы данных g — вектор начальных значений а,Ь,с |
Регрессия синусоидой f (x) =a-sin (x+b) +c |
15.2.3 |
| sine (z) |
z — аргумент |
Sine-функция |
10.11 |
| slope (x, y) |
х,у — векторы данных |
Коэффициент а линейной регрессии b+а-х |
15.2.1 |
| sort (v) |
v — вектор |
Сортировка элементов вектора |
9.2.4 |
| sph2xyz (г,O,ф) |
r,0,ф — сферические координаты |
Преобразование сферических координат в прямоугольные |
10.10 |
| stack(A,B,C, . . . ) |
А,В,С,... — векторы или матрицы |
Слияние матриц сверху вниз |
9.2.2 |
| Stiffb (y0, t0, t1, M, D, J) |
См. rkfixed J ( t , у ) — матричная функция Якоби для D(t,y) |
Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом Булирша-Штера |
11.5.2 |
| Stiffb (y0, t0, t1, acc, D, J, k, s) |
См. rkadapt J ( t , у ) — матричная функция Якоби для D(t,y) |
Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом Булирша-Штера (для определения только последней точки интервала) |
11.5.2 |
| Stiffr (y0, t0, t1, M, D, J) |
См. Stiffb |
Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом Розен-брока |
11.5.2 |
| stiffr (y0, t0, t1, acc, D, J,k,s) |
См. stiffb |
Возвращает матрицу с решением задачи Коши для жесткой системы ОДУ методом Розен-брока (для определения только последней точки интервала) |
11.5.2 |
| str2num(S) |
S — строка |
Преобразование строкового представления в действительное число |
10.7 |
| str2vec(S) |
S — строка |
Преобразование строкового представления в вектор ASCII-кодов |
10.7 |
| strlen(S) |
s — строка |
Количество знаков в строке |
10.7 |
| subma-trix(A, ir , jr , ic, jc) |
А — матрица ir, jr — строки ic, jc — столбцы |
Возвращает часть матрицы, находящуюся между i г , j г-строками и ic.jc-столбцами |
9.2.2 |
| substr (S,m,n) |
s — строка |
Подстрока, полученная из строки S выделением п знаков, начиная с позиции m в строке S |
10.7 |
| supsmooth(x,y) |
х,у — векторы данных |
Сглаживание с помощью адаптивного алгоритма |
15.3.1 |
| svd(A) |
A — действительная матрица |
Сингулярное разложение |
9.5.4 |
| svds (A) |
A — действительная матрица |
Вектор, состоящий из сингулярных чисел |
9.5.4 |
| tan(z) |
z — аргумент |
Тангенс |
10.4 |
| tanh ( z ) |
z — аргумент |
Гиперболический тангенс |
10.5 |
| Tcheb(n,x) |
x — аргумент n — порядок |
Полином Чебышева первого рода |
10.6 |
| tr(A) |
А — квадратная матрица |
След матрицы |
9.1.8 |
| trunc (x) |
х — аргумент |
Целая часть числа |
10.8 |
| Ucheb(n,x) |
х — аргумент n — порядок |
Полином Чебышева второго рода |
10.6 |
| vec2str (v) |
v — вектор ASCII-кодов |
Строковое представление элементов вектора V |
10.7 |
| wave ( у ) |
у — вектор данных |
Вектор прямого вейв-лет-преобразования |
15.4.2 |
| WRITE* (file) |
file— строковое представление пути к файлу |
Запись данных в файл типа * |
16.6 |
| xy2pol(x,y) |
х,у — прямоугольные координаты на плоскости |
Преобразование прямоугольных координат в полярные |
10.10 |
| xyz2cyl (x,y, z) |
x,y,z— прямоугольные координаты |
Преобразование прямоугольных координат в цилиндрические |
10.10 |
| xyz2sph(x,y, z) |
x,y,z — прямоугольные координаты |
Преобразование прямоугольных координат в сферические |
10.10 |
| Y0(x) Yl(x) Yn(m,x) |
х — аргумент, х>0 |
Функция Бесселя второго рода нулевого, первого и m-го порядка |
10.1.1 |
| ys (n,x) |
n — порядок х — аргумент |
Сферическая функция Бесселя второго рода |
10.1.5 |
Некоторые функции, составляющие семейства типовых функций, приведены в сокращенном виде с недостающей частью имени в виде звездочки *. Например, различные статистические функции, описывающие различные распределения, или функции вывода в файлы. Подробные сведения содержатся в разделе, на который указывает соответствующая ссылка.
 5GL
5GL
|
|
|