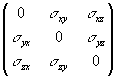 , (12)
, (12)5. Mathematical model of quasielastic ether.
As early as 1839 on the basis of the usual theory of elasticity MacCullagh developed concepts of the ethereal medium, which appeared to be in agreement with the theory of electromagnetic and optical phenomena by J.C. Maxwell (1864). Below the equations of MacCullagh are given mainly in Arnold Sommerfeld's presentation [12]. In the theory of continuum, displacements, gyrations and strains are usually considered. An elastic body reacts to a strain by the rise of a tensor of elastic forces, the strains are also described by a tensor. Now let us imagine a "quasi-elastic" body, which is unreceptive to compression-tensile strains, but reacts to torsional strain relative to absolute space. A mathematical description of such shear strains can be given by an antisymmetric tensor. We can represent the strains applied to unit cube sides as antisymmetric tensor:
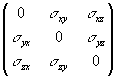 , (12)
, (12)
where s ik = -s ki.
The relation between a rotation and strains are shown in Fig. 10. The elementary volume D t is turned by an angle of j z (an arrow around the positive direction of the z-axis, according to the rule of right-handed screw).
Fig. 10. Relation between strains and twisting moment in a quasi-elastic body.
To realize such torsion it is necessary to apply a moment of force around the z-axis:
Mz = kjz Dt, (13)
where k is the "torsion modulus" of a quasi-elastic body. Two shearing forces s xy and s xy designated in the figure, in the x- and y-planes, plotted on the axes x and y in positive directions and antiparallel forces in the relevant planes along the axes in negative directions, correspond to this moment of force. To observe a correspondence between (12) and (13) we should get
s xy = - syx = (k/2)jz. (14)
As a result we obtain the moment operating in both ї-
planes:2s xyD yD z(D x/2) = (k/2)j zD t
and the moment operating in two y-planes
- 2s yxD xD z(D y/2) = (k/2)j zD t ,
as well as the moment from equation (13).
The cyclical substitution from (14) explicitly leads to the following expressions:
syz = - szy = (k/2)jx, szx = - sxz = (k/2)jy . (14a)
The action of forces, given in Fig. 10, can be represented schematically as those applied to an infinitesimal material point, situated inside a certain body.
It is possible to write down the motion equations of this quasi-elastic body by analogy with the known motion equations from the theory of elasticity [54]. Compiling them, we should take into account inertia (d - is the mass of a unit volume) and consider only conventionally slow motions. Besides, we should abandon exterior forces (¦ = 0). Then, taking into account (14) and (14р), we shall get
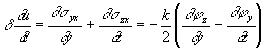 .
.
The latter, cyclically converted and vectorial written, represents an equation of motion
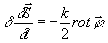 (15)
(15)
This equation can be represented in another way, using the ratio between 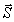 and the angular velocity v
. It will happen, if here we exchange dj
/dt for ¶
j
/¶
too
and the angular velocity v
. It will happen, if here we exchange dj
/dt for ¶
j
/¶
too
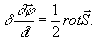 (16)
(16)
Based on assumptions of medium incompressibility, for the value of 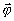 , - i.e. the angle of rotation of the displacement vector, we shall add the following condition:
, - i.e. the angle of rotation of the displacement vector, we shall add the following condition:
div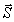 = 0, div
= 0, div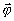 = 0. (17)
= 0. (17)
According to A. Sommerfeld [12], the set of equations (15), (16) and (17) demonstrates a convincing simplicity and symmetry. It has the same shape, as equations of J.C. Maxwell for vacuum.
For more detailed investigation we shall introduce an electric field strength  , a magnetic intensity
, a magnetic intensity 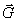 , the constants of proportionality a
, b
, whose dimensions will depend on a choice of a physical quantities system, in which
, the constants of proportionality a
, b
, whose dimensions will depend on a choice of a physical quantities system, in which  and
and 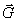 are expressed and also on the sign before the magnetic field charge and force:
are expressed and also on the sign before the magnetic field charge and force:
р)
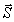 = -a
= -a
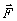 ,
, 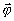 = ±
b
= ±
b
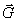 ,
,
or b) 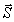 = -a
= -a
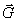 ,
, 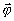 = ±
b
= ±
b
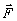 .
.
Then identically to equations (15), (16) and (17) we shall receive the following twice:
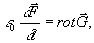 div
div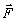 = 0, (18)
= 0, (18)
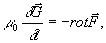 div
div 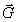 = 0.
= 0.
The abbreviations introduced here e 0, m 0 are termed dielectric and magnetic permeability of vacuum. In the system of our designations they will be given via:
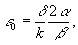
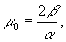 (18a)
(18a)

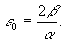 (18b)
(18b)
Their product is irrespective of the choice of a system of units (the coefficients a , b ). In both cases, this product will be equal to:
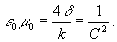 (19)
(19)
Thus, the particular value of C means the velocity of propagation in vacuum. Let us take note, that just as the Newtonian definition of velocity is bound up with the concept of elasticity, so C is bound with the torsion modulus k.
In a ponderable dielectric the same basic equations (18), as in vacuum, operate only with the changed values of e
, m
, instead of e
0, m
0.. However, both conditions of divergence will vary essentially. Instead of div = 0 there should be
= 0 there should be
div B = 0, where B = m is magnet induction. (20)
is magnet induction. (20)
This implies that a torsional deformation 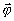 of a medium will be determined not by the value of
of a medium will be determined not by the value of 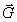 , but by the value of B creating no difficulties. On the other hand, the condition
, but by the value of B creating no difficulties. On the other hand, the condition 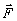 = 0 will transform into
= 0 will transform into
div D = de, where D = e is electrical strength, (21)
is electrical strength, (21)
where d e is spatial density of an operating electrical charge.
Since not  , but
, but 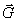 determines now the current velocity
determines now the current velocity 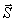 and the constants e
, m
, are bound with k, d
, a
and b
, J.C. Maxwell's equations can be valid here too, in a ponderable dielectric. In the work [12] A. Sommerfeld writes, that he is far from attaching any physical sense to this "model of ether". At the same time, the inclusion of the part about a model of quasi-solid ether into his fundamental work "Mechanics of deformable media", which latest edition was issued in 1978, is rather significant.
and the constants e
, m
, are bound with k, d
, a
and b
, J.C. Maxwell's equations can be valid here too, in a ponderable dielectric. In the work [12] A. Sommerfeld writes, that he is far from attaching any physical sense to this "model of ether". At the same time, the inclusion of the part about a model of quasi-solid ether into his fundamental work "Mechanics of deformable media", which latest edition was issued in 1978, is rather significant.
The strain of the ethereal medium arising around the conductor with current, Fig. 9, most clearly demonstrates the validity and adequacy of MacCullagh's concept. Torsional strain forms a number of nested concentric surfaces. Each of these surfaces is equipotential within which a magnetic field intensity is a constant.
Our proposition (see p.6 of section 3) that the ethereal medium, to some extent, is bound by great (according to astronomic scales) physical masses, corresponds to MacCullagh's earlier concept. In our opinion, the strains in the ethereal medium can be described by all tensor types in which diagonal terms, as in (12) are zero. It means that in the ethereal medium strains of shape-changes, i.e. torsion, twisting and shear may exist.
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|