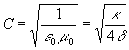
6. Density of the ethereal medium in a vacuum and in physical media.
On the basis, of the equation (19) from the previous section we can state, that the ethereal medium possesses some density d of an electromagnetic nature. Owing to the very high homogeneity of this medium (except for the areas close to physical bodies), the density, as well as the velocity of light C, is rather constant. This medium is in a sense an analogue of an omnipresent (distributed) fluid with constant density. But, it is necessary to consider such a medium or vacuum a material body, as it actively exhibits itself in electrical and magnetic fields and is the basis, in which electromagnetic waves propagate. Therefore, it is necessary to term the ethereal medium, Fig. 8, a distributed material body. Physical bodies of the higher-level organization (electrons, atoms, molecules etc.) are not distributed uniformly in space, as the ethereal medium. They are geometrically concentrated and represent clots of a material medium in particular points of space. It is necessary to term them concentrated material or physical bodies. This definition has also the sense, that physical bodies can be detected by physical devices. Of course, the properties of the ethereal medium can be determined by wave excitation in it, for example. However, the characteristics of an unexcited ethereal medium cannot be defined, because any physical device will change its state on measuring.
The density of the ethereal medium, as well as the density of a physical one, is one of the parameters defining the velocity of waves propagation in it. From the equation (19), given in the previous section, it is possible to find out, that the velocity of electromagnetic waves propagation in a vacuum is equal to
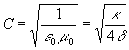
or
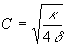
As follows from this equation, the torsion elasticity k, equivalent to the square of the light velocity should be very great. It could be determined, if the electromagnetic density of a vacuum d was known. The assessment of the density d can be made using the wave impedance equation for vacuum. As is known, the wave impedance of continuous media is defined by the formula:
R = dC, (24)
whence
d = R/C. (25)
The value of the vacuum wave impedance is precisely known [3],
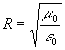, (26)
where m 0 is magnetic permeability, e 0 is the dielectric constant of vacuum. The velocity of light C can also be expressed as m 0 and e 0:
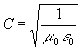. (27)
Substituting the expressions for R and C into the formula (25), we shall obtain
d = m0 = 1.25664×10-6, m kg×s-2a-2, (28)
where the density dimension is given in the SI system units.
Thus, the magnetic permeability m 0 plays the role of density (inertial mass) in the ethereal medium. Now we shall use A. Sommerfeld's formula (19) to determine the value of torsion modulus
к
= 4/e0 = 4.51763×1011, m3 kg×s-4a-2. (29)We mentioned in Sec. 2 that MacCullagh identified dielectric permeability e with the reciprocal of elasticity [11].
So, it uniquely follows from the definitions of d and k that the ethereal medium (vacuum) is of an electromagnetic nature. The exponents of these values give an idea of the value d as a very small one, and of the torsion modulus k as an extremely high one. The classical mechanics and the mathematical oscillation theory show with obviousness that wavelike processes can exist only given some distributed masses and elastic forces uniting the masses into an unbroken continuum. It is necessary to take into account, that for solid isotropic bodies there is a formula linking the values of the velocity V, mass and elastic modulus of a substance [53]:
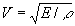, (30)
where Е
- is the elastic modulus, r is the substance density.A comparison of the formulas (23) and (30) shows, that they are similar. In the formula (30) the elastic modulus Е reflects the elasticity of links between particles in a solid body. The substance density r reflects the mass of these material points. As follows from the form of the formula (30), the velocity V in a solid (and not only in solid) body is higher in those substances, in which the links between material points (atoms, molecules) have greater force, the velocity is less in those, whose atoms and molecules are less massive. Many substances, in particular, diamond and lead, can exemplify this concept. As is known [56], diamond is noted for its great hardness and elasticity. For example, the value of the velocity of shear waves propagation in it is Vs = 12.32 km/s, with the density r = 3.51 g/cm3. At the same time in lead the velocity Vs = 0.86 km/s and the density is r = 11.6 g/cm3. A proportional dependence between the velocity Vs and the value 1/r , the inverse of the density, is well expressed for alkaline metals. Besides, simple mechanical models demonstrate the rule – the greater is the mass of unit cells in oscillating systems, the lower is the oscillation frequency and v.v. Accordingly, the greater is the elasticity of joints in the elementary cell, the higher is the oscillation frequency in the oscillation system and v.v. Adverting to the expression (29) we see, that the shear elasticity of the ethereal medium k is really very great. The comparison of the velocity of the shear wave propagation in elastic solid bodies with the velocity of light С indicates it. For example, the velocity of propagation of shear waves in the most elastic solid substance - diamond - is only 4.1·10-5 of the С value. Accordingly, the vacuum density should be very low, as follows from the C value (28). It is natural, that the electromagnetic values of d and k cannot be strictly compared with the relevant characteristics of solid bodies by virtue of their distinguishing physical nature.
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
