Еще в 1839 году на основе обычной теории упругости МакКулаг развил представления об эфирной среде, которые, как оказалось, хорошо согласуются с теорией электромагнитных и оптических явлений Д. Максвелла. Ниже уравнения МакКулага приводятся, в основном, в изложении Арнольда Зоммерфельда [12].

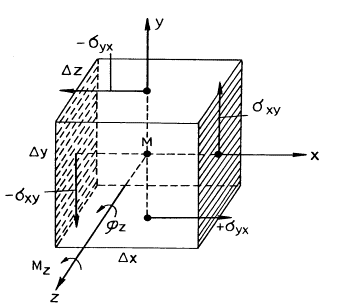
Рис. 10. Отношения между напряжениями и скручивающим моментом в <квазиупругом> теле.
В теории сплошных сред обычно рассматриваются перемещения, вращения и деформации. Упругое тело реагирует на деформации возникновением тензора упругих сил, причем деформации также описываются тензором. Теперь представим себе <квазиупругое> тело, которое невосприимчиво к деформациям сжатия-растяжения, но реагирует на деформацию кручения относительно абсолютного пространства. Так как такое кручение имеет характер антисимметричного тензора, мы можем представить напряжения, приложенные к сторонам элементарного куба в виде антисимметричного тензора. Запишем его в следующем виде
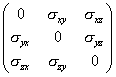 , , |
(12) |
где σik = − σki.
Cоотношения между поворотом и напряжениями отражены на схеме pис.10. Элементарный объем Δτ повернут на угол φz (стрелка вокруг положительного направления оси z, по правилу правого винта).
Чтобы осуществить такое скручивание, необходимо приложить момент силы вокруг z-оси:
| Mz = κφzΔτ , | (13) |
где κ есть <модуль скручивания> квазиупругого тела. Этому моменту силы соответствуют два обозначенные на рисунке сдвигающие напряжения σxy и −σyx на x- и y-плоскостях, отложенных на осях x и y в положительных направлениях и антипараллельные напряжения на соответствующих плоскостях осей в отрицательных направлениях. Чтобы соблюсти соответствие между (12) и (13) мы должны получить
| σxy = − σyx = (k/2)φz. | (14) |
В итоге мы получаем момент, действующий на обеих х-плоскостях:
| 2σxyΔyΔz(Δx/2) = (k/2)φzΔτ |
и момент на двух y-плоскостях
| − 2σyxΔxΔz(Δy/2) = (k/2)φzΔτ , |
также как и момент из уравнения (13).
Циклическая подстановка из (14) явно приводит к следующим выражениям:
| σyz = − σzy = (k/2)φx, σzx = − σxz = (k/2)φy. | (14a) |
Схему действия сил, приведенную на рис.10 можно представить как приложенную к бесконечно малой материальной точке, находящейся внутри некоего тела. Уравнения движения этого квазиэластичного тела можно написать по аналогии с известными из теории упругости уравнениями движения [53]. Составляя их, учтем инерцию (δ - масса единичного объема) и будем рассматривать только условно медленные движения. Кроме этого, мы должны отказаться от внешних сил (Р = 0). Тогда, с учетом (14) и (14а), получим
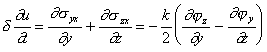 , , |
где u - смещение.
Последнее, циклически преобразованное и векториально записанное, представляет собой уравнение движения
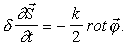 |
(15) |
Это уравнение можно отобразить иначе, через отношение между
вектором смещения 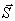 и угловой
скоростью
и угловой
скоростью 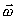 . Это произойдет,
если и здесь мы поменяем dφ/dt на
∂φ/∂t:
. Это произойдет,
если и здесь мы поменяем dφ/dt на
∂φ/∂t:
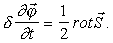 |
(16) |
Из предположения несжимаемости среды, для значения 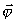 , - угла поворота вектора смещения,
добавим следующее условие:
, - угла поворота вектора смещения,
добавим следующее условие:
div 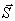 = 0, div = 0, div 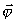 = 0. = 0. |
(17) |
Как отмечает А. Зоммерфельд [12], система уравнений (15), (16) и (17) демонстрирует убедительную простоту и симметрию. Она имеет ту же форму, что и уравнения Д.Максвелла для пустого пространства.
Для более подробного исследования введем напряженность
электрического поля 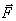 , напряженность
магнитного поля
, напряженность
магнитного поля 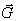 , коэффициенты
пропорциональности α, β, размерность которых будет
зависеть от выбора системы физических величин, в которых выражены
, коэффициенты
пропорциональности α, β, размерность которых будет
зависеть от выбора системы физических величин, в которых выражены
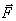 и
и 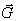 , а также от знака перед зарядом и силой
магнитного поля:
, а также от знака перед зарядом и силой
магнитного поля:
a) 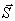 = +α = +α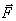 , , 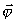 = = 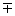 β β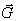 , , |
или
b) 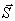 = +α = +α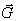 , , 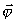 = = 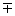 β β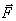 . . |
Тогда идентично уравнениям (15), (16) и (17), получим дважды:
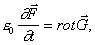 div div
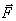 = 0, = 0, |
|
| (18) | |
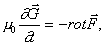 div div
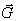 = 0. = 0. |
Введенные здесь сокращения ε0, μ0 называются диэлектрической и магнитной проницаемостью вакуума. В системе наших обозначений они будут даны через:
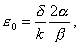 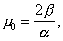 |
(18a) |
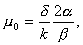 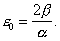 |
(18b) |
Их произведение независимо от выбора системы единиц (коэффициентов α, β). В обоих случаях это произведение будет равно:
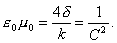 |
(19) |
Таким образом определенная величина С обозначает скорость распространения в вакууме. Обратим внимание на то, что С связано с модулем скручивания κ.
В весомом диэлектрике действуют такие же основные уравнения (18),
как и в вакууме, только с измененными значениями ε, μ,
вместо ε0, μ0. Но оба условия
дивергенции существенно изменятся. Вместо div 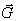 = 0 должно быть
= 0 должно быть
| div B = 0, | (20) |
где B = μ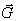 -
магнитная индукция.
-
магнитная индукция.
Это приведет к тому, что скручивание 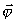 среды будет определяться не величиной
среды будет определяться не величиной
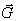 , но величиной В, что не
создает никаких трудностей. С другой стороны, условие
, но величиной В, что не
создает никаких трудностей. С другой стороны, условие 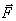 = 0 перейдет в
= 0 перейдет в
| div D = δe, | (21) |
где D = ε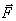 -
электрическая напряженность, δе - пространственная
плотность действующего электрического заряда. Так как теперь не
-
электрическая напряженность, δе - пространственная
плотность действующего электрического заряда. Так как теперь не 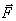 , а
, а 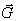 определяет скорость тока
определяет скорость тока 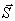 и
константы ε, μ связаны с κ, δ, α,
β, уравнения Д. Максвелла могут быть верными и здесь, в
весомом диэлектрике.
и
константы ε, μ связаны с κ, δ, α,
β, уравнения Д. Максвелла могут быть верными и здесь, в
весомом диэлектрике.
В своей работе [12] А. Зоммерфельд пишет, что он далек от того, чтобы этой <модели эфира> придать какой-либо физический смысл. Вместе с этим, само включение раздела о модели квазижесткого эфира в его капитальный труд <Механика деформируемых сред>, последнее издание которого выпущено в 1978 году, весьма знаменательно.
Наиболее убедительно верность и адекватность концепции МакКулага демонстрирует деформация эфирной среды, возникающая вокруг проводника с током, рис.9. Скручивающая деформация образует ряд вложенных друг в друга концентрических поверхностей. Каждая из этих поверхностей является эквипотенциалью, в пределах которой напряженность магнитного поля обладает одинаковой величиной.
Наше положение (см. п.6 раздела 3) о том, что эфирная среда в известной степени связана (закреплена) большими по астрономическим масштабам физическими массами соответствует ранее выдвинутой МакКулагом концепции. По нашему мнению, напряжения в эфирной среде описываются всеми видами тензоров, в которых диагональные члены, как и в (12) равны нулю. Это означает, что в эфирной среде могут существовать деформации формоизменения, т.е. скручивания, кручения и сдвига.
Причем, здесь и далее под деформацией скручивания мы будем понимать деформации, возникающие при приложении момента сил, когда прямая линия (ось) его приложения проходит через тело, а само тело закреплено на бесконечности (рис.10). Деформация кручения возникает тогда, когда тело закреплено между двумя параллельными плоскостями и одна из плоскостей поворачивается, оставаясь параллельной первой, на некоторый угол относительно другой. Деформация сдвига происходит в теле, закрепленном между двумя параллельными плоскостями, причем одна плоскость сдвигается параллельно первой по прямой линии.
|
|