Главной темой этой главы является трехмерная графика. Начнем мы с обзора методов,
позволяющих достичь объемности получаемых образов, а в конце главы будут описаны
методы построения анимационных программ.
Глава завершает базовый курс изучения основ OpenGL, и после ее изучения читатель
сможет создавать высококачественные трехмерные изображения.
Примеры к главе помещены на дискете в каталоге Chapter3.
Параметры вида
В предыдущей главе мы убедились, что объем сцены ограничен кубом с координатами
точек вершин по диагоналям (-1, -1, -1) и (1, 1, 1). Начнем дальнейшее изучение
с того, что увеличим объем этого пространства. Проект из подкаталога ExOl нам
поможет. На сцене присутствует все тот же треугольник, одну из вершин которого
можно перемещать по оси Z нажатием клавиши <пробел>, значение координаты
вершины выводится в заголовке окна. Теперь мы видим треугольник целиком в пределах
большего, чем раньше, объема.
Код перерисовки окна выглядит так:
wglMakeCurrent(Canvas.Handle, hrc);
glViewport(0, 0, ClientWidth, ClientHeight);
9lPushMatrix;
glFrustum (-1, 1, -1, 1, 3, 10); // задаем перспективу
glTranslatef(0.0, 0.0, -5.0); // перенос объекта по оси 1
9lClearColor (0.5, 0.5, 0.75, 1.0);
glClear (GL_COLOR_BUFFER_BIT) ;
glColor3f (1.0, 0.0, 0.5);
glBegin (GLJTRIANGLES);
glVertex3f (-1, -1, 0);
glVertex3f (-1, 1, 0) ;
glVertexSf (1, 0, h);
glEnd;
glPopMatnx;
SwapBuffers (Canvas.Handle);
wglMakeCurrent (0, 0) ;
Основная последовательность действий заключена между командами giPushMatrix
и glPopMatrix. Если этого не делать, то при каждой перерисовке окна, например,
при изменении его размеров, сцена будет уменьшаться в размерах.
Здесь встречается новая для нас команда - giFrustum, задающая параметры вида,
в частности, определяющие область воспроизведения в пространстве. Все, что выходит
за пределы этой области, будет отсекаться при воспроизведении. Первые два аргумента
задают координаты плоскостей отсечения слева и справа, третий и четвертый параметры
определяют координаты плоскостей отсечения снизу и сверху. Последние аргументы
задают расстояния до ближней и дальней плоскостей отсечения, значения этих двух
параметров должны быть положительными - это не координаты плоскостей, а расстояния
от глаза наблюдателя до плоскостей отсечения.
Замечание
Старайтесь переднюю и заднюю плоскости отсечения располагать таким образом,
чтобы расстояние между ними было минимально возможным чем меньший объем ограничен
этими плоскостями, тем меньше вычислений приходится производить OpenGL
Теперь все, что рисуется с нулевым значением координаты Z, не будет видно наблюдателю,
поскольку ближнюю плоскость отсечения мы расположили на расстоянии трех единиц
от глаза наблюдателя, располагающегося в точке (0, 0, 0). Поэтому перед воспроизведением
треугольника смещаем систему координат на пять единиц вниз.
Треугольник удалился от наблюдателя, и его вершины располагаются уже не на границе
окна, а сместились вглубь экрана.
Замечание
В главе 6 мы узнаем, как соотнести пространственные и оконные координаты, если
видовые параметры заданы с помощью команды glFrustum
Переходим к следующему примеру - проекту из подкаталога Ех02 отличие от первого примера состоит в том, что команды giPushMatrix И glPopMatrix удалены, а перед вызовом команды giFrustum стоит вызов команды giboadidentity. Будем понимать это как действие "вернуться в исходное состояние". При каждой перерисовке экрана перед заданием видовых параметров это следует проделывать, иначе объем сцены будет последовательно отсекаться из предыдущего.
Замечание
Устанавливать видовые параметры не обязательно при каждой перерисовке экрана,
достаточно делать это лишь при изменении размеров окна.
Это несложное соображение предваряет следующий пример - проект из подкаталога
Ех03. Для повышения надежности работы приложения пользуемся явно получаемой
ссылкой на контекст устройства, а не значением свойства canvas.Handle Сразу
же после получения контекста воспроизведения делаем его текущим в обработчике
события create формы, а непосредственно перед удалением освобождаем контекст
в обработчике Destroy.
Теперь такие параметры OpenGL, как цвет фона и цвет примитивов, можно задавать
единственный раз - при создании формы, а не выполнять это действие каждый раз
при перерисовке экрана. В отличие от всех предыдущих проектов, в данном появляется
отдельный обработчик события, связанного с изменением размеров окна. Напомню,
раньше при этом событии выполнялся тот же код, что и при перерисовке окна.
Во всех оставшихся примерах, как правило, будет присутствовать отдельный обработчик
события, связанного с изменением размеров окна. В этом обработчике задается
область вывода и устанавливаются параметры вида, после чего окно необходимо
перерисовать:
procedure TfrmGL.FormResize(Sender: TObject);
begin
glViewport (0, 0, ClientWidth, ClientHeight);
glLoadldentity;
giFrustum (-1, 1, -1, 1, 3, 10); // видовые параметры
glTranslatef (0.0, 0.0, -5.0); // начальный сдвиг системы координат
InvalidateRect(Handle, nil. False);
end;
Код, связанный с перерисовкой окна, теперь сокращается и становится бо-лее читабельным:
Procedure TfrmGL.FormPaint(Sender: TObject);
WClear (GL_COLOR_BUFFER_BIT);
9lBegin (GLJTRIANGLES) ;
glVertex3f (-1, -1, 0) ;
glVertex3f (-l, 1, 0);
glVertex3f (1, 0, h);
glEnd;
SwapBuffers(DC);
end;
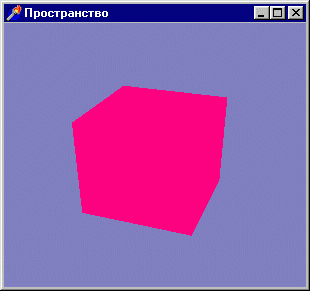
Хоть мы уже и рисуем пространственные картинки, однако почувствовать трехмерность пока не могли. Попробуем нарисовать что-нибудь действительно объемное, например, куб (проект из подкаталога Ex04). Результат работы программы - на рис. 3. 1.

Рис. 3. 1. В будущем мы получим более красивые картинки, начинаем же с самых простых
Для придания трехмерности сцене поворачиваем ее по осям:
procedure TfrmGL. FormResize(Sender: TObject);
begin
glViewport(0, 0, ClientWidth, ClientHeight);
glLoadIdentity;
glFrustum (-1, 1, -1, 1, 3, 10); // задаем перспективу
// этот фрагмент нужен для придания трехмерности
glTranslatef (0. 0, 0. 0, -8. 0); // перенос объекта - ось Z
glRotatef (30. 0, 1. 0, 0. 0, 0. 0); // поворот объекта - ось X
glRotatef (70. 0, 0. 0, 1. 0, 0. 0); // поворот объекта - ось Y
InvalidateRect(Handle, nil, False);
end;
Построение куба сводится к построению шести квадратов, отдельно для каждой стороны фигуры:
glBegin (GL_QUADS);
glVertex3f (1. 0, 1. 0, 1. 0);
glVertex3f (-1. 0, 1. 0, 1. 0);
glVertex3f (-1. 0, -1. 0, 1. 0);
glVertex3f (1. 0, -1. 0, 1. 0);
glEnd;
glBegm (GLJ2UADS);
glVertex3f (1. 0, 1. 0, -1. 0);
glVertex3f (1. 0, -1. 0, -1. 0);
glVertex3f (-1. 0, -1. 0, -1. 0),
glVertex3f (-1. 0, 1. 0, -1. 0);
glEnd;
glBegin (GL_QUADS);
glVertex3f (-1. 0, 1. 0, -1. 0);
glVertex3f (-1. 0, 1. 0, -1. 0);
glVertex3f (-1. 0, -1. 0, 1. 0);
glVertex3f (-1. 0, -1.0, 1.0);
glEnd;
glBegin (GL_QUADS);
glVertex3f (1. 0, 1. 0, 1. 0);
glVertex3f (1. 0, -1. 0, 1. 0);
glVertex3f (1. 0, -1. 0, -1. 0);
glVertex3f (1. 0, 1. 0, -1. 0);
glEnd;
glBegin (GL_QUADS);
glVertex3f (-1. 0, 1. 0, -1. 0);
glVertex3f (-1. 0, 1. 0, 1. 0);
glVertex3f (1. 0, 1. 0, 1. 0);
glVertex3f (1. 0, 1. 0, -1. 0);
glEnd;
glBegin(GL_QUADS);
glVertex3f (-1. 0, -1. 0, -1. 0);
glVertex3f (1. 0, -1. 0, -1. 0);
glVertex3f (1. 0, -1. 0, 1. 0);
glVertex3f (-1. 0, -1. 0, 1. 0);
glEnd;
Код получается громоздким, согласен.
Замечание
Для некоторых базовых фигур мы сможем в будущем найти возможность сократить
код, но в общем случае объемные объекты строятся именно так, т e из отдельных
плоских примитивов.
Я хочу предостеречь вас на случай, если вы желаете прямо сейчас потренироваться
и нарисовать что-нибудь интересное. Пока что наши примеры сильно упрощены, могут
быть только учебной иллюстрацией и не годятся в качестве шаблона или основы
для построения более серьезных программ Получившаяся картинка действительно
трехмерная, но пространственность здесь только угадывается: куб залит монотонным
цветом, из-за чего плохо понятно, что же нарисовано. Сейчас это не очень важно,
мы только учимся задавать видовые параметры. Для большей определенности в ближайших
примерах будем рисовать каркас куба, как, например, в следующем примере - проекте
из подкаталога Ex05 (рис. 3. 2).
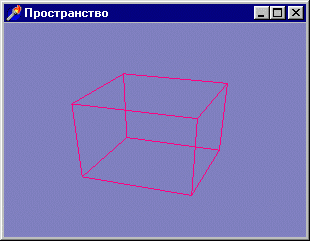
Рис. 3. 2. Для ориентировки в пространстве будем рисовать каркасную модель куба
Чтобы выводить только ребра куба, после установления контекста воспроизведения
задаем нужный режим воспроизведения полигонов:
glPolygonMode (GL_FRONT_AND_BACK, GL_LINE);
Получившаяся картинка иллюстрирует важную вещь: использование команды glFrustum
приводит к созданию перспективной проекции. Хорошо видно, что ребра куба не
параллельны друг другу и имеют точку схода где-то на горизонте.
Чтобы помочь вам лучше разобраться с одной из важнейших команд библиотеки OpenGL,
я написал пример, расположенный в подкаталоге Ех06. В этом примере аргументы
команды - переменные:
glFrustum (vLeft, vRight, vBottom, vTop, vNear, vFar);
Нажатием на пробел можно приблизить точку зрения к сцене, если при этом удерживать
клавишу <Shift>, точка зрения будет удаляться.
Чтобы приблизить точку зрения, варьируем с помощью первых четырех аргументов
параметры перспективы, уменьшая объем сцены, для удаления в пространстве проводим
обратную операцию. Затем заново обращаемся к обработчику Resize формы, чтобы
установить параметры перспективы в обновленные значения и перерисовать окно.
If Key = VK_SPACE then begin
If ssShift in Shift then begin // нажат Shift, удаляемся
vLeft: = vLeft - 0. 1;
vRight: = vRight + 0. 1;
vBottom: = vBottom - 0. 1;
vTop: = vTop + 0. 1;
end
else begin // приближаемся
vLeft: = vLeft + 0. 1;
vRight: = vRight - 0. 1;
vBottom: = vBottom + 0. 1;
vTop: = vTop - 0. 1;
end;
FormResize(nil);
end;
Аналогично клавишами управления курсором можно манипулировать значениями каждой
из этих четырех переменных в отдельности, а клавиши <Insert> и <Delete>
отвечают за координаты ближней и дальней плоскостей отсечения.
Так, если чересчур близко к наблюдателю расположить заднюю плоскость отсечения,
дальние ребра куба станут обрезаться (рис. 3. 3).
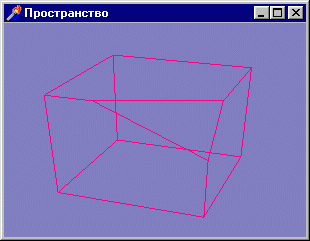
Рис. 3. 3. Вот что происходит с кубом, если заднюю плоскость приближать слишком близко
Еще один способ приблизить к сцене точку зрения - уменьшать значение координаты передней плоскости отсечения. Возможно, это более практичный способ, поскольку у первого способа есть один недостаток: если принижаться к сцене чересчур близко, картинка переворачивается и при дальнейишем "приближении" удаляется, оставаясь перевернутой.
Замечание
Это в принципе два разных способа навигации в пространстве, и, если быть точным,
оба они не перемещают точку зрения. Можно для этих нужд не изменять параметры
вида, а действительно смещать в пространстве систему координат.
Теперь мы перейдем к другой проекции - ортографической, параллельной. Посмотрим
проект из подкаталога Ех07, результат работы которого показан на рис. 3.4.
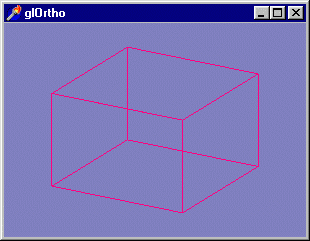
Рис. 3.4. Великий Леонардо нашел бы эту картинку нелепой, но чертежник
должен быть довольным
Отличается эта проекция от перспективной именно отсутствием перспективы. В обработчике
изменения размеров окна видовые параметры задаются с помощью команды giortho:
procedure TfrmGL.FormResize(Sender: TObject);
begin
glViewport(0, 0, ClientWidth, ClientHeight);
glLoadldentity;
glOrtho (-2, 2, -2, 2, 0, 15.0)
glTranslatef (0.0, 0.0, -10.0);
glRotatef (30.0, 1.0, 0.0, 0.0)
glRotatef (60.0, 0.0, 1.0, 0.0)
// видовые параметры
// перенос системы координат по оси Z
// поворот системы координат по оси X
// поворот системы координат по оси Y
InvalidateRect (Handle, nil, False);
end;
Аргументы команды giortho имеют точно такой же смысл, что и у giFrustum, но
последние два аргумента могут иметь отрицательное значение. Помимо этих двух
команд, OpenGL предоставляет еще несколько возможностей установки видовых параметров,
например, библиотека glu содержит команду giuOrtho2D. Эта команда имеет четыре
аргумента, смысл которых такой же, как и у giortho. По своему действию она эквивалентна
вызову giortho с указанием значения расстояния до ближней плоскости отсечения
равным минус единице, и расстоянием до дальней плоскости отсечения равным единице.
Как при такой проекции выглядит куб из предыдущих примеров, показано на рис.
3.5, а проект находится в подкаталоге Ех08.
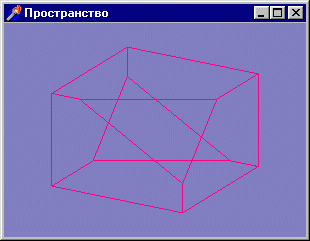
Рис. 3.5. Командой gluOrtho2D следует пользоваться с осторожностью, но с точки зрения скорости воспроизведения она является оптимальной
Обратите внимание, что здесь отсутствует начальный сдвиг по оси Z:
procedure TfrmGL.FormResize(Sender: TObject);
begin
glViewport(0, 0, ClientWidth, ClientHeight);
glLoadldentity;
gluOrtho2D (-2, 2, -2, 2); // задаем перспективу
glRotatef (30.0, 1.0, 0.0, 0.0); // поворот объекта - ось X
glRotatef (60.0, 0.0, 1.0, 0.0); // поворот объекта - ось Y
InvalidateRect(Handle, nil, False);
end;
Куб рисуется вокруг глаза наблюдателя и проецируется на плоскость экрана. Согласно
установкам этой команды передняя и задняя части нашего куба частично обрезаются.
Следующая команда, которую мы рассмотрим, пожалуй, наиболее популяр-на в плане
использования для первоначального задания видовых параметров. Команда gluPerspective,
как ясно из ее названия, также находится в библиотеке glu. Проект примера содержится
в подкаталоге Ех09, а полу-ЧаЮщаяся в результате работы программы картинка показана
на рис. 3.6.
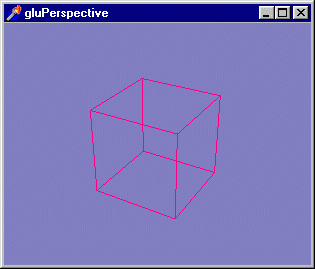
Рис. 3.6. Так работает команда gluPerspective
Смысл аргументов команды поясняется в комментариях:
Procedure TfrmGL.FormResize(Sender: TObject);
begin
glViewport(0, 0, ClientWidth, ClientHeight);
glLoadIdentity
// задаем перспективу
gluPerspective(30. 0, // угол видимости в направлении оси Y
ClientWidth / ClientHeight, // угол видимости в направлении оси X
1 0, // расстояние от наблюдателя до ближней плоскости отсечения
15. 0); // расстояние от наблюдателя до дальней плоскости отсечения
glTranslatef (0. 0, 0. 0, -10. 0); // перенос - ось Z
glRotatef (30. 0, 1. 0, 0. 0, 0. 0); // поворот-ось X
glRotatef (60. 0, 0. 0, 1. 0, 0. 0); // поворот-ось Y
InvalidateRect (Handle, nil, False);
end;
Замечание
В главе 4 мы узнаем, как соотносятся аргументы команд gluPerspective и glFrustum.
С перспективами, конечно, надо попрактиковаться. Настоятельно рекомендую разобраться с примером из подкаталога Ex10. Клавиши управления курсором позволяют манипулировать значениями первых двух аргументов команды gluPerspective. При уменьшении первого аргумента происходит приближение глаза наблюдателя к сцене, уменьшение второго аргумента приводит к тому, что сцена растягивается в поперечном направлении (рис. 3 7).
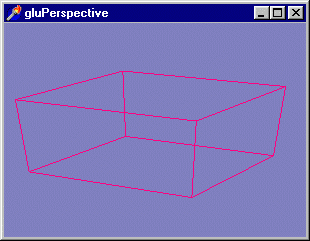
Рис. 3. 7. Изменения в видовых установках приводят к трансформации объектов на экране
Замечание
Как правило, в качестве значения второго аргумента команды gluPerspective, так
называемого аспекта, задают отношение ширины и высоты области вывода.
В проекте из подкаталога Ex11 я объединил все примеры на изученные команды установки видовых параметров (рис. 3. 8).
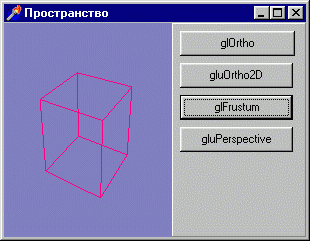
Рис. 3. 8. Команды задания видовых параметров
Вы имеете возможность еще раз уяснить различия между этими способами подготовки
сцены.Библиотека glu располагает еще одной вспомогательной командой, имеющей
отношение к рассматриваемой теме - gluLookAt. У нее девять аргументов: координаты
позиции глаза наблюдателя в пространстве, координаты точки, располагающейся
в центре экрана, и направление вектора, задающего поворот сцены (вектор "up").
При использовании этой команды можно обойтись без начальных операций со сдвигом
и поворотом системы координат. Ее работу демонстрирует проект из подкаталога
Exl2 (рис. 3. 9).
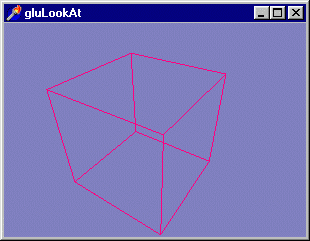
Рис. 3. 9. Командой gluLookAt удобно пользоваться при перемещениях точки зрения в пространстве
При задании параметров вида ограничиваемся минимумом команд:
glLoadIdentity;
gluPerspective (50. 0, ClientWidth / ClientHeight, 2. 0, 10. 0);
gluLookAt (2.7, 2, 2.5, 0.4, 0.5, 0.5, О, О, 1);
InvalidateRect(Handle, nil, False);
На рис 3.10 показаны экранные формы, выдаваемые программой из подкаталога Ех13.
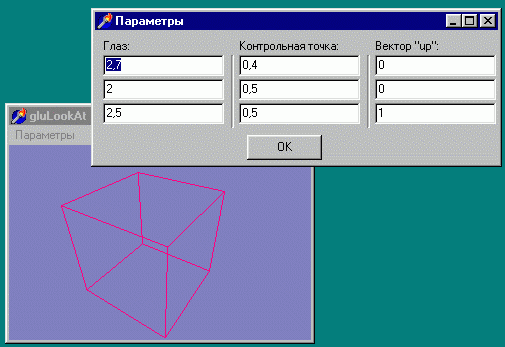
Рис 3. 10. Команду gluLookAt нужно изучить основательно
В них можно менять значения всех аргументов команды gluLookAt, и поскольку этих
аргументов сравнительно много, я создал вспомогательную форму, в полях редактирования
которой выводятся и задаются пользователем координаты всех девяти аргументов
Рекомендую обязательно попрактиковаться с этим примером, чтобы "почувствовать"
работу параметров Обратите внимание, что, как подчеркивается в документации,
вектор "up" не должен быть параллельным линии, соединяющей точку зрения
и контрольную точку
Матрицы OpenGL
При обсуждении команд giRotatef и giTransiatef мы уже обращали внимание на то,
что их действие объясняется с позиций линейной алгебры Например, про команду
giTransiatef в соответствующем файле справки говорится, что эта команда умножает
текущую матрицу на матрицу переноса Аналогично giRotatef сводится к операции
перемножения текущей матрицы на матрицу поворота Многие изученные нами команды,
действие которых я объяснял по их функциональному смыслу, в действительности
описываются с помощью базовых понятий раздела математики, изучающего вопросы,
связанные с геометрическими операциями, например, такими, как проекция Надеюсь,
отсутствие ссылок на линейную алгебру нисколько не помешало вам при изучении
предыдущего материала Если я говорю, что команда giscale является командой масштабирования
(и умалчиваю о том, что она сводится к операции перемножения матриц), то рассчитываю
на то, что читателю данной информации будет вполне достаточно для успешного
использования этой команды на практике
Я сознательно не включил в лекции изложение математических основ для всех подобных
команд, поскольку замыслил ее прежде всего как практическое руководство по компьютерной
графике Мне кажется, что многие читатели не очень хотели бы особо углубляться
в дебри формул Это отнюдь не значит, что я пытаюсь принизить значение математической
грамотности Просто мой опыт преподавания подсказывает, что очень многие программисты
предпочитают руководства, делающие упор на практике К счастью, существует масса
литературы по компьютерной графике, уделяющей много внимания математике, где
подробно рассказывается об операциях перемножения матриц и прочих подобных вопросах
Если вы все-таки испытаете необходимость в более основательной теоретической
подготовке, найти подходящее пособие не составит большого труда. Однако и в
нашей практической книжке без представления о некоторых специальных терминах
не обойтись. Ограничимся самым необходимым.В OpenGL имеется несколько важных
матриц Матрица модели ("modelview matrix") связана с координатами
объектов Она используется для того, чтобы в пространстве построить картину как
бы видимую глазу наблюдателя. Другая матрица, матрица проекций ("piojection
matirx"), связана с построением проекций пространственных объектов на плоскость.Матрица
проекций, имея координаты точки зрения, строит усеченные ("clip")
координаты, по которым после операций, связанных с перспективой, вычисляются
нормализованные координаты в системе координат устройства ("normalized
device coordinates") После трансформаций, связанных с областью вывода,
получаются оконные координаты.Координаты вершин в пространстве и на плоскости
проекций четырехмерные, помимо обычных координат есть еще w-координата Поэтому
матрица модели и матрица проекций имеют размерность 4x4. Перенос и поворот системы
координат сводится к операции перемножения матриц, связанных с текущей системой
координат, и матриц переноса и поворота Библиотека OpenGL располагает набором
команд, связанных с этими операциями, а также имеет универсальную команду для
перемножения матриц giMuitMatrix При желании и наличии математической подготовки
этой командой можно заменить команды переноса, поворота и ряд других Посмотрим,
как это делается.
В проекте из подкаталога Ех14 команда начального переноса заменена командой
giMuitMatrix Для этого введен массив 4x4, хранящий матрицу переноса:
rat . Array [0. 3, 0. 3] of GLfloat,
Матрица переноса заполняется нулями, кроме элементов главной диагонали, которые должны быть единицами, и последней строки, содержащей вектор переноса В примере перемещение осуществляется только по оси Z:
mt [0, 0] := 1;
№ [1, 1] := 1;
№ [2, 2] := 1;
mt [3, 3] := 1;
mt [3, 2] := -8;
Стартовый сдвиг теперь осуществляется так:
glMultMatrixf (@mt);
Если надо вернуться к исходной позиции, текущая матрица заменяется матрицей
с единицами по диагонали и равными нулю всеми остальными элементами, единичной
матрицей Это и есть действие команды giLoadidentity Она является частным случаем
более универсальной команды giLoadMatnx, предназначенной для замены текущей
матрицы на заданную, ссылка на которую передается в качестве аргумента.
Без примера эти команды не усвоить, поэтому загляните в подкаталог Exl5 Массив
mt аналогичен единичной матрице. Команда glLoadidentity отсутствует, вместо
ее вызова используется явная загрузка единичной матрицы:
glLoadMatrixf (@mt);
После знакомства с матричными операциями становится яснее технический смысл
команд glPushMatrix и glPopMatrix, запоминающих в стеке текущую матрицу и извлекающих
ее оттуда. Такая последовательность манипуляций выполняется быстрее, чем вызов
glLoadMatrix. To же самое можно сказать и по поводу glLoadidentity, т. e. единичная
матрица загружается быстрее
командой glLoadidentity, чем glLoadMatrix.
Замечание
Чем реже вы пользуетесь командами манипулирования матрицами, тем быстрее будет
работать программа Но учтите, что если на сцене присутствует не больше пары
десятков объектов, все манипуляции с матрицами съедают один кадр из тысячи.
Узнать, какая сейчас установлена матрица, можно с помощью команды glGet. Во
всех наших предыдущих примерах мы задавали параметры вида применительно к матрице,
установленной по умолчанию Определим, какая это матрица.
Подкаталог Ex16содержит проект, который нам в этом поможет Обработчик Resize
формы дополнен выводом в заголовке окна имени текущей матрицы:
var
wrk: GLUInt; begin
glGetIntegerv (GL_MATRIX_MODE, @wrk);
case wrk of
GL_MODELVIEW: Caption: = 'GL_MODELVIEW';
GL_PROJECTION: Caption: = 'GL_PROJECTION';
end;
Запустив проект, выясняем, что по умолчанию в OpenGL установлена матрица модели. Итак, во всех предыдущих примерах операции производились над матрицей модели. В любой момент мы можем выяснить значение этой матрицы. Проиллюстрируем примером - проектом из подкаталога Exl7. При создании формы массив 4x4 заполняется матрицей модели:
glGetFloatv (GL_MODELVIEW_MATRIX, @mt);
при выборе пункта меню появляется вспомогательное окно, в котором выводится текущая матрица модели (рис 3. 11).
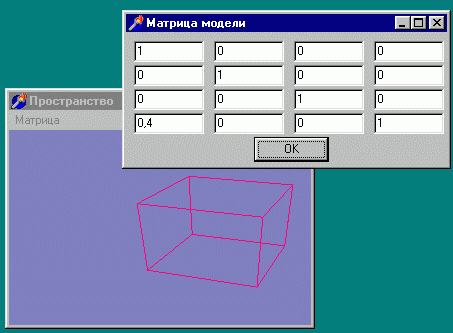
Рис. 3. 11. Вывод содержимого матрицы модели
При первом появлении окна эта матрица совпадает с единичной матрицей по главной диагонали единицы, все остальные элементы равны нулю Команда glLoadidentity в этой программе также заменена явной загрузкой матрицы. В проекте имеется возможность варьировать загружаемую матрицу, по нажатию на кнопку "OK" она устанавливается в модели. Сейчас у вас имеется прекрасная возможность попрактиковаться в матричных операциях. Например, числа на главной диагонали являются масштабными множителями по осям. Поменяйте первые из этих двух чисел произвольно для масштабирования по осям X и Y.
Замечание
Для одного из примеров следующей главы нам важно уяснить, что нулевое значение
первого или второго из диагональных элементов приведет к проекции сцены на плоскость.
Если вы внимательно прочитали этот раздел, то полученных знаний о матрицах
теперь достаточно для того, чтобы нарисовать все что угодно Осталось узнать
еще одну команду - glMatrixMode Она позволяет установить текущую матрицу.
Проекты всех предыдущих примеров подходят только для простейших пространственных
построений, таких как рисование каркаса кубика Для более сложных программ они
не годятся из-за одного упрощения.
для корректного вывода пространственных фигур параметры вида задаются при Установленной
матрице проекции, после чего необходимо переключить- ся в пространство модели.
То есть обычная последовательность здесь, например, такая:
glViewport(0, 0, ClientWidth, ClientHeight);
glMatnxMode (GL_PROJECTION);
glLoadldentity;
glFrustum (-1, I, -I, I, 3, 10);
glMatrixMode (GL_MODELVIEW);
glLoadldentity;
Замечание
На простейших примерах мы не почувствуем никакой разницы и не поймем, что же
изменилось Позже я попробую показать, с чем связана необходимость выполнения
именно такой последовательности действий.
Напоминаю, что параметры вида обычно помещаются в обработчике изменения размеров окна Стартовые сдвиги и повороты обычно располагаются здесь же, а код воспроизведения сцены заключается между командами glPushMatrix И glPopMatrix. Иногда поступают иначе: код воспроизведения начинается с glLoadldentity, а далее идут стартовые трансформации и собственно код сцены
Замечание
Поскольку программы профессионалов, как правило, основываются на первом подходе,
именно его я буду использовать в большинстве примеров этих лекций.
Сейчас мы рассмотрим пару примеров на темы предыдущей главы, которые мы не могли
рассмотреть раньше из-за того, что в них используются команды задания вида.
Начнем с проекта из подкаталога Ех18 - модификации классической программы, поставляемой
в составе OpenGL SDK. Программа рисует точку и оси системы координат (рис. 3.12).
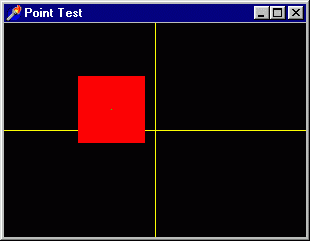
Рис. 3.12. Результат работы проекта Point Test
Клавишами управления курсором можно передвигать точку, нажатием клавиши 'W' размер точки можно уменьшать, если же нажимать эту клавишу есте с <shift>, то размер точки увеличивается. Первая цифровая клавиша задает режим сглаживания точки. Обратите внимание, что при установленном режиме сглаживания размер получающегося кружочка ограничен некоторыми пределами, для точек больших размеров он не вписывается точно в квадрат точки. Если точнее, то в примере рисуется две точки - вторая рисуется зеленым цветом посередине первой. Вторая точка не изменяется в размерах и всегда выводится несглаженной, но с единичным размером. Пример можно использовать в качестве простого теста, скорость передвижения большой по размеру точки позволяет оценить возможности компьютера. Посмотрите внимательно, как в этом примере задаются видовые параметры. Здесь интересно то, что плоскости отсечения привязаны к текущим размерам окна:
glViewport(О, О, ClientWidth, ClientHeight);
glMatrixMode(GL_PROJECTION);
glLoadldentity;
gluOrtho2D(-ClientWidth/2, ClientWidth/2, -ClientHeight/2, ClientHeight/2);
glMatrixMode(GL_MODELVIEW);
glLoadldentity;
Теперь при изменении размеров окна картинка не масштабируется, а изменяются
размеры видимой части пространства. Если точку поставить вблизи границы окна,
при уменьшении его размеров точка пропадает, выходит за пределы видимости. В
примерах предыдущей главы в такой ситуации точка перемешалась внутрь окна пропорционально
его размерам.
Координаты точки хранятся в массиве трех вещественных чисел, вершина воспроизведения
задается командой с окончанием "v". Аргументом в этом случае является
указатель на массив:
glBegin(GL_POINTS);
glVertex3fv (@point);
glEnd;
Замечание
Напоминаю, что эта - векторная - форма команд является оптимальной по скоростным
показателям
Следующий пример, проект из подкаталога Ех19, тоже может использоваться в качестве
простого теста скоростных характеристик компьютера. Рисуется серия отрезков
прямых, наподобие разметки циферблата часов. В начале и в конце каждого отрезка
рисуются точки В примере видовые параметры опираются на конкретные числа.
glViewport(0, 0, ClientWidth, ClientHeight);
glMatrixMode(GL_PROJECTION);
glLoadIdentity;
gluOrtho2D (-175, 175, -175, 175);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity;
Поэтому при изменении размеров окна картинка масштабируется так, что вся сцена
всегда вписывается в экран.
Клавиша 'W' все так же позволяет регулировать ширину линий, первые две цифровые
клавиши отведены для управления двумя режимами воспроизведения: первый режим
включает штриховку линий, второй задает сглаживание отрезков.
Управляя этими тремя параметрами, можно получать разнообразные картинки, например
такую, как приведена на рис. 3. 13.
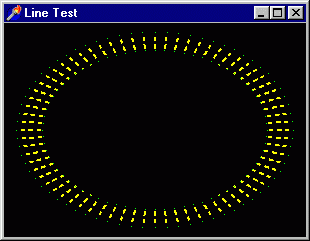
Рис. 3. 13. Получить такие узоры на самом деле легко
Поработав с данным примером, вы должны уяснить для себя, что и для сглаженных
отрезков есть ограничение - по ширине.
Также полезно разобраться, как в этом примере рисуется система отрезков Два
массива задают координаты начала и конца единственного отрезка, этот отрезок
рисуется в цикле, и каждый раз происходит поворот на пять градусов:
glLineWidth(size); // ширина отрезка
If model // режим, задающий штриховку отрезков
then glEnable(GL_LINE_STIPPLE) // использовать штриховку
else glDisable(GL_LINE_STIPPLE); // не использовать штриховку
If mode2 // режим, задающий сглаженность отрезков
then glEnable (GL_LINE_SMOOTH) // сглаживать отрезки
else glDisable(GL_LINE_SMOOTH); // не использовать сглаженность
glPusnMatrix; // запоминаем систему координат
For i: = 0 to 71 do begin // цикл рисования 72 отрезков
glRotatef(5. 0, 0, 0, 1); // поворот на пять градусов
glColor3f(1. 0, 1. 0, 0. 0); //цвет отрезков - желтый
glBegin(GL_LINE_STRIP); // примитив - отрезок
glVertex3fv(@pntA); // указатель на начало отрезка
glVertex3fv(@pntB); / указатель на конец отрезка
glEnd;
glColor3f(0. 0, 1. 0, 0. 0); // цвет точек - зеленый
glBegin(GL_POINTS); // примитив - точка
glVertex3fv(@pntA); // точка в начале отрезка
glVertex3fv(@pntB); // точка в конце отрезка
glEnd;
end;
glPopMatrix; // возвращаемся в первоначальную систему координат
Буфер глубины
При создании контекста воспроизведения в число параметров формата пикселов входят
размеры разделов памяти, предоставляемой для нужд OpenGL, или буферов. Помимо
буферов кадра, в OpenGL присутствуют еще три буфера: буфер глубины, буфер трафарета
и вспомогательный буфер
Для специальных нужд могут использоваться еще буфер выбора и буфер обратной
связи, они подготавливаются пользователем по мере надобности.
Работа с буферами будет нами подробно изучена в соответствующих разделах курса.
В этом разделе мы познакомимся с буфером глубины. Как ясно из его названия,
он используется для передачи пространства При воспроизведении каждого пиксела
в этот буфер записывается информация о значении координаты Z пиксела, так называемая
оконная Z. Если на пиксел приходится несколько точек, на экран выводится точка
с наименьшим значением этой координаты.
При пространственных построениях отказ от использования буфера глубины приводит
к неверной передаче пространства. Посмотрим, в чем тут дело. Для удобства отладки
я написал процедуру, строящую оси координат и помечающую оси буквами X, Y и
Z:
Procedure Axes;
var
Color: Array [1.. 4] of GLFloat;
begin
glPushMatrix;
glGetFloatv (GL_CURRENT_COLOR, @Color),
glScalef (0. 5, 0. 5, 0. 5);
glColor3f (0, 1, 0);
glBegin (GL_LINES);
glVertex3f (0, 0, 0);
glVertex3f (3, 0, 0);
glVertex3f (0, 0, 0);
glVertex3f (0, 3, 0);
glVertex3f (0, 0, 0);
glVertex3f (0, 0, 3);
glEnd;
// буква X
glBegin (GL_LINES)
glVertex3f (3. 1,-0. 2, 0. 5);
glVertex3f (3. 1,0. 2, 0. 1);
glVertex3f (3. 1,-0. 2, 0. 1);
glVertex3f (3. 1,0. 2, 0. 5);
glEnd;
// буква Y
glBegin (GL_LINES);
glVertex3f (0. 0, 3. 1, 0. 0);
glVertex3f (0. 0, 3. 1, -0. 1);
glVertex3f (0. 0, 3. 1, 0. 0);
glVertex3f (0. 1, 3. 1, 0. 1);
glVertex3f (0. 0, 3. 1, 0. 0);
glVertex3f (-0. 1, 3. 1, 0. 1);
glEnd;
// буква Z
glBegin (GL_LINES);
glVertex3f (0. 1, -0. 1, 3. 1);
glVertex3f (-0. 1, -0. 1, 3. 1);
glVertex3f (0. 1, 0. 1, 3. 1);
glVertex3f (-0. 1, 0. 1, 3. 1);
glVertex3f (-0. 1, -0. 1, 3. 1);
glVertex3f (0. 1, 0. 1, 3. 1);
glEnd;
// Восстанавливаем значение текущего цвета
glColor3f (Color [1], Color [2], Color [3])
glPopMatrix;
end;
обраатите внимание, что оси рисуются зеленым цветом, а цветовые установ-запоминаются
во вспомогательном массиве, по которому они восстанавливаются в конце работы
процедуры.
Оси выходят из точки (0, 0, 0) и визуализируются лишь в положительном направлении.
Проект находится в подкаталоге Ex20. В качестве основы взят пример glFrustum,
в который добавлен вызов вышеописанной процедуры и убрано контурное отображение
куба. Результат работы программы приведен на рис. 3. 14. Видно, что пространство
передается некорректно, куб полностью загораживает оси координат, хотя оси должны
протыкать грани куба.
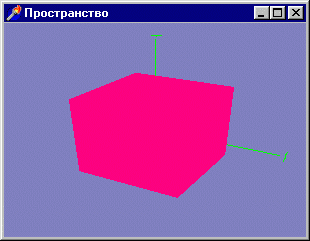
Рис. 3. 14. Без использования буфера глубины пространство сцены передается некорректно
В следующем примере, проекте из подкаталога Ex21, та же сцена выводится верно (рис. 3. 15).
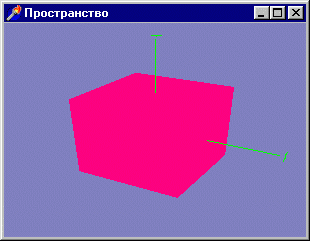
Рис. 3. 15. Теперь правильно: оси протыкают грани куба
После получения контекста воспроизведения сообщаем системе OpenGL о том, что
необходимо корректировать построения в соответствии с глубиной:
glEnable (GL_DEPTH_TEST); // включаем режим тестирования глубины
Код сцены начинается с очистки двух буферов: буфера кадра и буфера глубины:
glClear (GL_COLOR_BUFFER_BIT or GL_DEPTH_BUFFER_BIT); // + буфер глубины
Точно так же, как перед очередным построением необходимо очистить поверхность рисования, для корректного воспроизведения требуется очистить буфер пространства. Эта действия, которые мы впервые выполнили в этом примере, будут использоваться в большинстве последующих примеров.
Замечание
О содержимом буфера глубины мы будем говорить еще неоднократно
С буфером глубины связаны две команды: glDepthFunc И glDepthRange. Хоть они
применяются довольно редко, представление о них иметь не помешает. Первая из
этих команд задает правило, по которому происходит сравнение значения оконного
Z перед выводом пиксела. По умолчанию установлено значение GL_LESS - выводить
на экран точки с минимальным значением оконной Z. Остальные значения приводят
чаще всего к тому, что вообще ничего не будет выведено.
Вторая команда задает распределение оконной координаты Z при переводе из нормализованных
координат в оконные. На рис. 3. 16 приведен результат работы программы (проект
из подкаталога Ex22), где такое распределение установлено в обратное принятому
по умолчанию:
glDepthRange (1, 0);
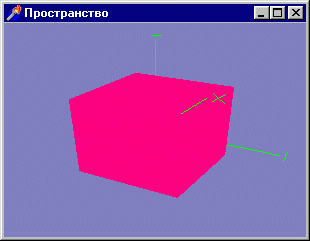
Рис. 3. 16. В любой момент можно увидеть то, что скрыто от глаза наблюдателя
Источник света
Предыдущие примеры вряд ли могут удовлетворить кого-либо в силу своей невыразительности.
Рисуемый кубик скорее угадывается, все грани покрыты монотонным цветом, за которым
теряется пространство. Теперь мы подо-шли к тому, чтобы увеличить реализм получаемых
построений.
Вот в следующем примере кубик рисуется более реалистично - рис. 3. 17, проект
из подкаталога Ex23.
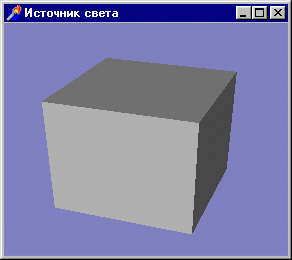
Рис. 3. 17. Нa сцене появился источник света
При создании окна включается источник света:
glEnable (GL_LIGHTING); // разрешаем работу с освещенностью
glEnable(GL_LIGHTO); // включаем источник света
Это минимальные действия для включения источника света. Теперь в сцене присутствует
один источник света с именем 0.
При необходимости можно "установить" несколько источников, для этого
точно так же используется команда glEnable, например:
glEnable (GL_LIGHT1); // включаем источник света 1
Пока нет смысла использовать дополнительные источники света, это никак не повлияет
на получаемые картинки, поскольку все добавляемые источники света используют
установки, принятые по умолчанию, и ничем не отличаются друг от друга.
При рисовании каждой стороны куба задается вектор нормали, используемый для
расчета цветовых параметров каждого пиксела. Для сокращения кода из шести сторон
куба я оставил три непосредственно видимые наблюдателю.
glBegin (GL_QUADS);
glNormal3f(0. 0, 0. 0, 1. 0);
glVertex3f(1. 0, 1. 0, 1. 0);
glVertex3f(-1. 0, 1. 0, 1. 0);
glVertex3f(-1. 0, -1. 0, 1. 0);
glVertex3f(1. 0, -1. 0, 1. 0);
glEnd;
glBegin(GL_QUADS);
glNormal3f(-1. 0, 0. 0, 0. 0);
glVertex3f(-1. 0, 1. 0, 1. 0);
glVertex3f(-1. 0, 1. 0, -1. 0);
glVertex3f{-1. 0, -1. 0, -1. 0)
glVertex3f(-1. 0,-1. 0,1. 0);
glEnd;
glBegin(GL_QUADS);
glNormal3f(0. 0, 1. 0, 0. 0);
glVertex3f(-1. 0, 1. 0, -1. 0);
glVertex3f(-1. 0, 1. 0, 1. 0);
glVertex3f(1. 0, 1. 0, 1. 0);
glVertex3f(1. 0, 1. 0, -1. 0);
glEnd;
Теперь поговорим о некоторых деталях.
выясним какое максимальное число источников света мы можем использовать. Проект
из подкаталога Ex24 в заголовке окна выводит это получаемое при создании окна,
с помощью команды glGet:
glGetintegerv (GL_MAX_LIGHTS, @wrk);
Caption: = intToStr (wrk);
Вектора нормалей строятся перпендикулярно каждой стороне куба. В силу того,
что наш кубик строится вокруг точки (0, 0, 0), аргументы glNomal3f в данном
случае совпадают с точкой пересечения диагоналей каждой грани куба. Чтобы уяснить,
насколько важно верно задавать вектор нормали, посмотрите пример, располагающийся
в подкаталоге Ex25.
Здесь рисуется только передняя грань кубика, тремя клавишами управления курсором
можно менять координаты вектора нормали. При этом меняется вид картинки: освещенность
площадки передается в соответствии с текущим значением вектора нормали.
Вектор нормали не обязательно должен исходить именно из середины площадки, достаточно
того, чтобы он был параллелен действительному вектору нормали к площадке. Это
иллюстрирует проект из подкаталога Ex26, где теми же клавишами можно передвигать
площадку в пространстве, а вектор нормали задается единожды при создании окна:
glNormal3f(-1. 0, 0. 0, 0. 0);
Где бы ни располагалась в пространстве площадка, она освещается единообразно.
Замечание
По умолчанию источник света располагается где-то в бесконечности, поэтому освещенность
площадки не меняется вместе с ее перемещением.
В примере из подкаталога Ex27 клавишей <курсор влево> задается поворот
площадки в пространстве вокруг оси Y, чтобы можно было взглянуть на площадку
с разных точек зрения. Если мы смотрим на заднюю сторону площадки, то видим,
что она окрашивается черным цветом. В некоторых ситуациях необходимо, чтобы
при таком положении точки зрения наблюдателя примитив не отображался вообще,
например, при воспроизведении объектов, образующих замкнутый объем, нет необходимости
тратить время на воспроизведение примитивов, заведомо нам не видимых, раз они
повернуты к нам задней стороной. Запомните, как это делается, разобрав проект
из подкаталога Ex28.
Здесь площадка не рисуется, если повернута к наблюдателю задней стороной. Для
этого необходимо включить отсечения задних сторон многоугольников:
glEnable (GL_CULL_FACE);
Команда glcullFace позволяет задавать, какие стороны при этом подвергаются отсечению, передние или задние. Понятно, что по умолчанию предлагается отсекать задние стороны. Противоположное правило отсечения можно установить так:
glCullFace (GL_FRONT);
Объемные объекты
Подчеркну еще раз, что для объемных построений используются все те же десять
изученных нами во второй главе примитивов.
В следующем примере строится объемный объект на базе тестовой фигуры, знакомой
нам по первой главе (рис. 3. 18). Проект расположен в подкаталоге Ex29.
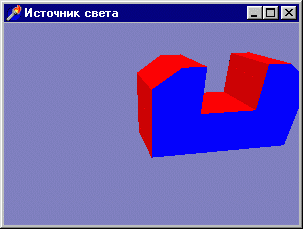
Рис. 3. 18. Теперь деталь стала объемной
Шестнадцать отдельных многоугольников образуют то, что наблюдателю представляется
единым объемным объектом.
В проекте введена переменная, ответственная за режим воспроизведения детали:
mode
(POINT, LINE, FILL) = LINE;
В зависимости от значения этой переменной устанавливается режим рисования многоугольников:
case mode of
POINT: glPolygonMode (GL_FRONT_AND_BACK, GL_POINT);
LINE: glPolygonMode (GL_FRONT_AND_BACK, GL_LINE);
FILL: glPolygonMode (GL_FRONT_AND BACK, GL FILL);
end;
режим можно менять, нажимая на первые три цифровые клавиши, а кла-иши управления
курсором позволяют изменять положение точки зрения в пространстве.
В этом примере деталь получается разноцветной. При включенном источнике света
для того, чтобы включить учет текущего цвета примитивов, необдимо вызвать команду
glEnable с соответствующим аргументом:
(GL COLOR MATERIAL);
Попутно обращу ваше внимание на то, что если объект приближается чересчур близко к глазу наблюдателя и пересекает ближнюю плоскость отсечения в нем появляется дырка, сквозь которую можно заглянуть внутрь объекта.
Замечание
Необходимо сказать, что при рисовании очень больших объектов происходят сильные
искажения, связанные с перспективой, поэтому рекомендуется объекты масштабировать
таким образом, чтобы их линейные характеристики лежали в пределах 100.
Надстройки над OpenGL
Существует несколько надстроек над OpenGL, представляющих собой набор готовых
команд для упрощения кодирования Стандартной надстройкой, поставляемой вместе
с OpenGL, является библиотека glu, физически располагающаяся в файле glu32 dll
Мы уже изучили несколько команд этой библиотеки, и в дальнейшем продолжим ее
изучение. Помимо этой стандартной надстройки наиболее популярной является библиотека
glut Для программистов, пишущих на языке С, эта библиотека особенно привлекательна,
поскольку является независимой от операционной системы Ее применение значительно
упрощает кодирование программ, поскольку вся черновая работа по созданию окна,
заданию формата пиксела, получению контекстов и пр выполняется с помощью вызовов
библиотечных функций Вот пример начальной части программы, где с использованием
функций библиотеки glut создается окно с заданными параметрами
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(400, 400);
glutInitWindowPosition(50, 50);
glutCreateWindow(argv[0]);
Программисты, работающие с Delphi, также могут пользоваться этой библиотекой. В приложении я привожу адрес, по которому можно получить заголовочный файл для подключения библиотеки Однако при программировании на Delphi мы не получим независимости от операционной системы, а из команд библиотеки чаще всего программистов интересует только набор функций для построения некоторых объемных фигур Поэтому вместо нестандартной библиотеки я предпочитаю использовать модуль DGLUT pas - перенос на Delphi исходных файлов библиотеки glut Во многих последующих примерах будут встречаться обращения к этоМУ модулю, соответствующие команды начинаются с префикса glut Например, для рисования куба с единичной длиной ребра вместо двух десятков строк теперь достаточно одной
glutSolidCube (1. 0);
Ломимо куба, модуль (и библиотека) содержит команды воспроизведения сферы, тора, конуса и некоторых правильных многогранников, таких как раэдр и додекаэдр Есть здесь и команда для рисования классического объекта для тестовых программ машинной графики - чайника. Правильные многогранники строятся как совокупность многоугольников, о том, как создаются остальные объекты этой библиотеки, мы поговорим позднее. Для получения представления о модуле DGLUT разберите несложный пример, проект из подкаталога Ех30. По выбору пользователя можно построить любой объект модуля в одном из режимов точками, линиями или сплошной поверхностью Для задания типа объекта и режима воспроизведения введены переменные типа "перечисление"
mode: (POINT, LINE, FILL) = FILL;
glutob]: (CUBE, SPHERE, CONE, TORUS, DODECAHEDRON,
ICOSAHEDRON, TETRAHEDRON, TEAPOT) = CUBE;
По умолчанию заданы значения, соответствующие кубу со сплошными гранями При воспроизведении сцены устанавливается режим и производится обращение к нужной команде
case mode of
POINT glPolygonMode (GL_FRONT_AND_BACK, GL_POINT);
LINE: glPolygonMode (GL_FRONT_ANDJ3ACK, GL_LINE);
FILL: glPolygonMode (GL_FRONT_AND_BACK, GL_FILL);
end;
case glutobj of
TEAPOT: glutSolidTeapot (1. 5);
CUBE: glutSolidCube (1. 5);
SPHERE: glutSolidSphere (1. 5, 20, 20);
CONE: glutSolidCone (0. 5, 1. 5. 20, 20);
TORUS: glutSolidTorus (0. 5, 1 5, 20, 20);
DODECAHEDRON: glutSolidDodecahedron;
ICOSAHEDRON: glutSolidIcosahedron;
TETRAHEDRON: glutSolidTetrahedron; end,
Нажимая на первые три цифровые клавиши, можно задавать режим, четвертая клавиша позволяет переключать тип объектаЖ
If Key = 52 then begin
inc (glutobj); // установить следующее значение
If glutobj > High (glutob]) then glutobj: = Low (glutobj);
InvalidateRect(Handle, nil, False);
Параметр команды, рисующей чайник, имеет такой же смысл, что и для куба, - размер объекта Для сферы необходимо указать радиус и количество линий разбиения по широте и по долготе.
Замечание
Чем больше эти числа, тем более гладкими получаются объекты но тем больше времени
требуется для их воспроизведения Если все предыдущие рекомендации по оптимизации
скоростных характеристик дают малоощутимый эффект, то детализация поверхностей
является одним из самых важных факторов, влияющих на скорость воспроизведения.
Для конуса задаются радиус основания, высота и пара чисел,
задающих гладкость построений
У тора параметры следующие внутренний и внешний радиусы и все те же два числа,
задающих, насколько плавной будет поверхность рисуемой фигуры
В этом примере режим задается способом, знакомым нам по предыдущим примерам
- командой glPolygonMode Для каркасного изображения объектов модуль располагает
серией команд, аналогичных тем, что мы используем в этом примере, но с приставкой
glutWire вместо glutSolid
Следующий пример показывает, как можно манипулировать объектами исходного набора,
чтобы получить другие объемные фигуры В подкаталоге Ex31 содержится проект,
представляющий модификацию классической программы из SDK B программе моделируется
рука робота в виде двух параллелепипедов (рис 3 19).
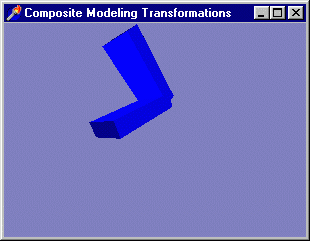
Рис. 3. 19. В программе рукой манипулятора можно управлять
Я не стал расписывать каждый параллелепипед по шести граням, а просто задал масштаб по трем осям перед воспроизведением куба так, чтобы вытянуть его в нужную фигуру
glTranslatef (-1. 0, 0. 0, 0. 0);
glRotatef (shoulder, 0. 0, 0. 0, 1 0);
glTranslatef (1 0, 0 0, 0. 0);
glPushMatrix; // запомнить текущий масштаб
glScalef (2 0, 0. 4, 1. 0); // для вытягивания куба в параллелепипед
glutSolidCube(1. 0); // в действительности - параллелепипед
alPopMatrix; // вернуть обычный масштаб
// вторая часть руки робота
glTranslatef (1. 0, 0. 0, 0. 0);
glRotatef (elbow, 0. 0, 0. 0, 1. 0);
glTranslatef (1. 0, 0. 0, 0. 0);
glPushMatrix;
glScalef (2. 0, 0. 4, 1. 0);
glutSolidCube(1. 0);
glPopMatrix;
В программе клавишами <Home>, <End>, <Insert> и <Delete> можно задавать относительное положение "суставов" руки, эмулируя управление рукой робота Первой цифровой клавишей можно менять режим воспроизведения, клавишами управления курсором можно менять положение точки зрения наблюдателя
Quadric-объекты библиотеки glu
Библиотека glu предоставляет набор команд, без которых, в принципе, можно обойтись,
но с их использованием решение многих задач сильно упрощается.
Для упрощения построений некоторых поверхностей второго порядка вводится серия
команд, основой которых являются квадратичные (quadric) объекты - собственный
тип этой библиотеки
Как и раньше, познакомимся с новой темой на примерах, для чего откройте проект
gluDisk dpr в подкаталоге Ex32 To, что получается в результате работы программы,
изображено на рис 3.20.
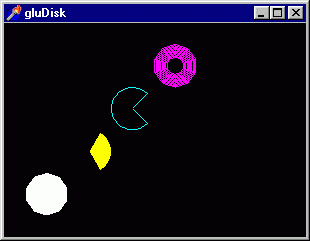
Рис. 3.20. Проект иллюстрирует использование quadnc-объектов
Пример этот является переложением на Delphi классической программы из набора
примеров OpenGL SDK Прежде всего обратите внимание, что видовые параметры задаются
в зависимости от пропорций окна, чтобы при любых значениях габаритов окна сцена
не выходила за его пределы:
ClientWidth <= ClientHeight
then glOrtho (0. 0, 50. 0, 0. 0, 50. 0 * ClientHeight / ClientWidth,
-1. 0, 1. 0)
else glOrtho (0. 0, 50. 0 * ClientWidth / ClientHeight, 0 0, 50 0,
-1. 0, 1. 0);
Для работы с командами библиотеки glu вводится переменная специального:
quadobj: GLUquadricObj;
При создании окна вызываем команду, создающую quadnc-объект, без этого действия обращение к объекту приведет к исключениям:
quadObj = gluNewQuadric,
Режим воспроизведения объекта задается командой giuQuadncDrawstyie, первым
аргументом команды указывается имя quadnc-объекта По умолчанию стиль задается
сплошным, так что чаще всего нет надобности вызывать эту команду Она также является
аналогом команды giPoiygonMode и всегда может быть ею заменена, за исключением
случая использования с аргументом GLU_SILHOUETTE При установлении такого режима
рисуется только граничный контур фигуры, отдельные сектора не рисуются, как
это сделано при рисовании третьего диска рассматриваемого примера
Диск строится с помощью команды giuDisk Помимо имени объекта ее аргументами
задаются внутренний и внешний радиусы, затем два числа, задающих число разбиений
диска по оси Z и число концентрических окружностей при разбиении диска Смысл
этих величин хорошо виден при каркасном режиме воспроизведения, когда в получающейся
паутинке хорошо видны отдельные сектора диска
В этом примере показано, как нарисовать дугу диска, сектор, "кусок пирога"
Это делается с помощью команды giuPartiaiDisk, первые пять napavseT-ров которой
полностью аналогичны параметрам giuDisk, а остальные задают начальный угол и
угол развертки Углы задаются в градусах По окончании работы память, используемую
quadnc-объектами, необходимо освобождать Сделать это нужно до освобождения контекста
воспроизведения:
gluDeleteQuadric (quadObj); // удаление объекта
wglMakeCurrent (О, О);
wglDeleteContext(hrc) ;
Замечание
Согласно файлу справки, обращение к удаленному объекту невозможно Может быть,
вы столкнетесь здесь с тем же неожиданным явлением что и я поставьте вызов этой
команды сразу же за его созданием и запустите программу У меня не возникло никаких
исключений, что меня удивило и озадачило Тем не менее, я все же порекомендую
не забывать удалять quadnc-объекты.
Библиотека glu имеет средства работы с возможными исключениями, для этого предназначена
команда giuQuadncCaiiback Первый аргумент, как обычно, имя quadnc-объекта, вторым
аргументом может быть только константа GLU_ERROR, третий аргумент - адрес функции,
вызываемой при исключении.
В заголовочном файле отсутствует описание константы GLU_ERROR, вместо нее можно
использовать присутствующую там константу GLU_TESS_ERROR, либо самому определить
такую константу.
Замечание
Точнее, описание константы не отсутствует, а закомментировано.
Без примера, конечно, не обойтись, им станет проект из подкаталога Ех30. В примере описаны процедура, которая будет вызываться в случае ошибки, и нужная константа:
procedure FNGLUError;
begin
ShowMessage ('Ошибка при работе с quadric-объектом1'),
end,
const
GLUJiRROR = GLU TESS ERROR;
Замечание
Процедура, используемая в таких ситуациях, не может присутствовать в описании
класса. При описании подобных процедур рекомендую использовать ключевое слово
stdcall.
Разу после создания quadnc-объекта задается функция, вызываемая при исключениях, здесь передаем адрес пользовательской процедуры:
WuQuadricCallbackfquadOb], GLU_ERROR, @FNGLUError);
Для того чтобы протестировать программу, создается исключение указанием заведомо
неверной константы в команде установки режима:
gluQuadricDrawStyle (quadObn, GL_LINE);
Замечание
Исключение при этом не снимается, так что после этого сообщения появляется сообщение
операционной системы об аварийной ситуации Можно использовать защищенный режим,
чтобы такого сообщения не появлялось.
Если при обращении к команде gluQuadricCallback в качестве адреса функции задать
значение, равное nil, возникающие исключения будут сниматься, а выполнение программы
будет продолжаться со строки, следующей за строкой, породившей исключение.
Помимо диска, библиотека располагает командами рисования еще некоторых объектов,
например, команда gluCylinder предназначена для построения цилиндров и конусов.
Параметры команды следующие: имя объекта, радиусы основания и верхней части
и два числа, задающих частоту разбиения. Команда gluSphere, как ясно из ее имени,
упрощает построение сферы У нее четыре аргумента, второй аргумент является радиусом
сферы, остальные параметры традиционны для этой серии команд.
Все объекты библиотеки glu я собрал в одном проекте, располагающемся в подкаталоге
Ex34. Этот пример аналогичен примеру на объекты библиотеки glut: по выбору пользователя
рисуется объект заданного типа.
Здесь также демонстрируется действие команды gluquadricOrientation, задающей
направление нормали к поверхности объекта, внутрь или наружу Еще можно выяснить,
как сказывается на виде объекта работа команды gluQuadricNormals, определяющей,
строятся ли нормали для каждой вершины, для всего сегмента либо вообще не строятся.
Нажимая на первые четыре цифровые клавиши, можно задавать значения параметров:
режим, тип объекта, ориентацию нормалей и правило их построения.
В проекте введены соответствующие перечисления:
mode: 'POINT, LINE, FILL, SILHOUETTE) = FILL;
gluobj: (SPHERE, CONE, CYLINDER, DISK) = SPHERE;
orientation: (OUTSIDE, INSIDE) = OUTSIDE;
(NONE, FLAT, SMOOTH) = SMOOTH;
Первым аргументом всех команд является имя quadric-объекта, все возможные константы перечисляются в конструкциях case:
case mode of // режим воспроизведения
POINT: gluQuadricDrawStyle (quadObj, GLU_POINT); // точки
LINE: gluQuadricDrawStyle (quadOb], GLU_LINE); // линии
FILL: gluQuadricDrawStyle (quadObj, GLU_FILL); // сплошным
SILHOUETTE: gluQuadricDrawStyle (quadObj, GLU_SILHOUETTE); // контур
end;
case orientation of // направление нормалей
INSIDE: gluQuadricOrientation (quadObj, GLU_INSIDE); // внутрь
OUTSIDE: gluQuadricOrientation (quadOb], GLU_OUTSIDE); // наружу
end;
case normals of // правило построения нормалей
NONE: gluQuadricNormals (quadObj, GLU_NONE); // не строить
FLAT: gluQuadricNormals (quadObj, GLU_FLAT); // для сегмента
SMOOTH: gluQuadricNormals (quadObj, GLU_SMOOTH); // для каждой вершины
end;
case gluob3 of// тип объекта
SPHERE: gluSphere (quadOb], 1. 5, 10, 10); // сфера
CONE: gluCylinder (quadObj, 0. 0, 1. 0, 1. 5, 10, 10); // конус
CYLINDER: gluCylinder (quadOb3, 1. 0, 1. 0, 1. 5, 10, 10) // цилиндр
DISK: gluDisk (quadObj, 0. 0, 1. 5, 10, 5); // диск
end;
На рис. 3. 21 приводится одна из возможных картинок, получаемых с помощью этого проекта.
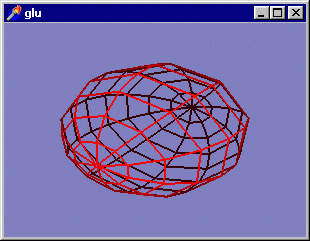
Рис. 3. 21. С помощью этого примера вы можете познакомиться со всеми
quadric-объектами Первым делом
Следующие примеры этого раздела также являются переложением на Delphi классических
примеров из SDK. Первым делом посмотрите проект из подкаталога Ех35 - вступительный
пример к нескольким следующим проектам и одновременно простейший пример на использование
объектов библиотеки glu.
Здесь просто рисуется сфера, модель звезды, наблюдатель находится над полюсом
(рис. 3.22).
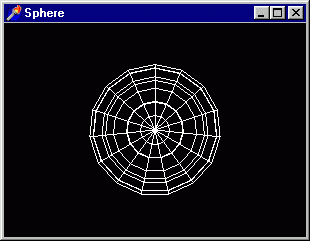
Рис. 3.22. Упрощенная модель звезды
Проект следующего примера располагается в подкаталоге Ех32, а экранная форма
приложения приведена на рис. 3.23.
Здесь моделируется уже планетарная система, клавишами управления курсором можно
задавать положение планеты относительно звезды и угол поворота ее вокруг собственной
оси.
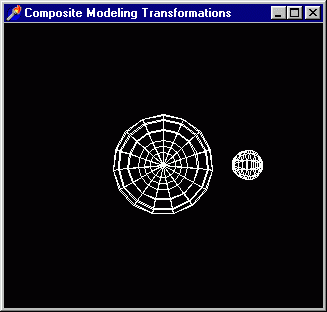
Рис. 3.23. Добавилась планета
Замечание
Начинающим я рекомендую хорошенько разобраться с этим примером, здесь впервые
для нас в пространстве присутствует несколько объектов, располагающихся независимо
друг от друга.
На базе одного quadric-объекта можно строить сколько угодно фигур; не обязательно
для каждой из них создавать собственный объект, если параметры всех их идентичны.
В этом примере на базе одного объекта рисуется две сферы:
// рисуем солнце
gluSphere (quadOb], 1.0, 15, 10);
// рисуем маленькую планету
glRotatef (year, 0.0, 1.0, 0.0);
glTranslatef (2.0, 0.0, 0.0);
glRotatef (day, 0.0, 1.0, 0.0);
gluSphere (quadOb], 0.2, 10, 10);
Следующий пример, проект из подкаталога Ех37, является небольшой модификацией предыдущего. Положение точки зрения изменилось так, что модель наблюдается под другим углом - рис. 3.24.

Рис. 3.24. В этом примере смотрим на систему с другой точки зрения
WPush слУжит хорошей иллюстрацией на использование команд glPushMatrix и glPopMatrix:
солнце и планета поворачиваются по отдельно-
°тносительно базовой системы координат:
glPushMatnx;
//Рисуем солнце
glpUshMatrix;
glRotatef (90. 0, 1. 0, 0. 0, 0. 0); // поворачиваем прямо
gluSphere (quadObj, 1. 0, 15, 10);
glPopMatrix;
// рисуем маленькую планету
glRotatef (year, 0. 0, 1. 0, 0. 0);
glTranslatef (2. 0, 0. 0, 0. 0);
glRotatef (day, 0. 0, 1. 0, 0. 0);
glRotatef (90. 0, 1. 0, 0. 0, 0. 0); // поворачиваем прямо
gluSphere (quadObj, 0. 2, 10, 10);
glPopMatrix;
Рано или поздно вам потребуется узнать, как в OpenGL можно получить вырезку пространственных фигур, например, полусферу. Следующий пример (подкаталог Ex38) поможет узнать, как это делается. В нем рисуется четверть сферы - рис. 3. 25
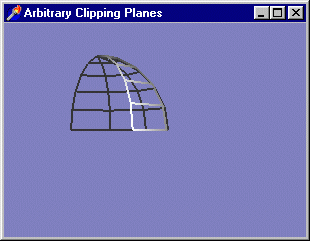 .
.
Рис. 3. 25. Совсем несложно получить полусферу или четверть сферы
Для вырезки части пространства используется новая для нас команда glclipplane.
Для вырезки можно использовать несколько плоскостей, эта команда идентифицирует
используемые плоскости. Первый аргумент -символическое имя плоскости вырезки,
второй - адрес массива, задающего эту плоскость. Символические имена начинаются
с CL__CLip_PLANE, дальше следует цифра, нумерация начинается с нуля.
При каждой вырезке отсекается полупространство, массив задает вектор, определяющий
остающуюся часть. Вектор не должен быть обязательно перпендикулярен осям, как
в нашем примере.
Для получения четверти сферы проделываем две вырезки: сначала обрезаем нижнее
полупространство, удаляя все вершины с отрицательным значением координаты Y,
затем отсекаем левое полупространство, т. e. удаляются вершины с отрицательным
значением координаты X:
const eqn: Array [0.. 3] of GLdouble = (0. 0, 1. 0, 0. 0, 0. 0);
eqn2: Array [0.. 3] of GLdouble = (1. 0, 0. 0, 0. 0, 0. 0);
// удаление нижней половины, для у < 0
glClipPlane (GL_CLIP_PLANEO, @eqn); // идентифицируем плоскость отсечения
alEnable (GL_CLIP_PLANEO); // включаем первую плоскость отсечения
// удаление левой половины, для x < 0
glClipPlane (GL_CLIP_PLANE1, @eqn2);
glEnable (GL_CLIP_PLANE1); // включаем вторую плоскость отсечения
Если теперь вернуться к библиотеке glut, то можно заметить, что сфера и конус в ней строятся на базе объектов библиотеки glu. Например, процедура для построения каркаса сферы выглядит так:
procedure glutWireSphere (
Radius: GLdouble;
Slices: GLint;
Stacks: GLint);
begin { glutWireSphere }
if quadObj = nil then
quadObj: = gluNewQuadric;
gluQuadricDrawStyle(quadObj, GLU_LINE);
gluQuadricNormals(quadObj, GLU_SMOOTH);
gluSphere(quadObj, Radius, Slices, Stacks);
end;
{ glutWireSphere }
Здесь можно подсмотреть несложный прием для определения того, надо ли создавать quadric-объект. Прием основан на том, что тип GLUquadricObj является указателем и его nil-значение соответствует тому, что объект пока еще не создан. Кстати, можете сейчас заглянуть в заголовочный файл opengl. pas, чтобы убедиться, что этот тип является указателем, указателем на пустую запись:
_GLUquadricObj = record end;
GLUquadricObj = ^_GLUquadricObj;
Заключительным примером раздела станет проект из подкаталога Ex39 - модель автомобиля (рис. 3. 26).
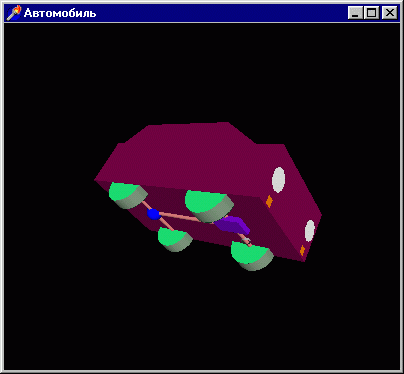
Рис. 3. 26. Мы можем строить модели и посложнее двух сфер
Клавишами управления курсором можно вращать модель по осям, клавиши Insert>
и <Delete> служат для приближения/удаления модели. Пробелом и клавишей
ввода можно задавать различные режимы воспроизведения.В примере используются
объекты библиотеки glu и модуля DGLUT. Нет смысла его подробно разбирать, остановимся
только на некоторых моментах. напоминаю, что для воспроизведения объектов с
различным пространстнным положением перед собственно воспроизведением каждого
из них система координат перемещается в нужную точку в пространстве. Для удобства
ориентирования в пространстве перед каждой трансформацией системы координат
текущую матрицу (систему координат) запоминаем вызовом команды glPushMatrix,
затем возвращаемся в эту систему координат вызовом glPopMatrix. Это будет выполняться
быстрее, чем обратные переносы но было бы лучше вычислять координаты следующего
объекта в текущей системе координат.Для разнообразия передние квадратные фары
автомобиля строятся с использованием команды gluDisk: если последние два аргумента
команды задать равными четырем, строится ромб, перед построением система координат
поворачивается:
glRotatef(45, 0. 0, 0. 0, 1. 0);
gluDisk (quadObj, 0. 0, 0. 1, 4, 4);
Квадраты задних фар строятся с помощью команды glRect, мы изучали эту команду
в предыдущей главе.
Для того чтобы нормаль квадрата была направлена в нужную сторону, пере ворачиваем
систему координат:
glRotatef(180, 1. 0, 0. 0, 0. 0); glRectf (0. 1, 0. 1, -0. 1, -0. 1);
Вместо этого можно было бы просто задать нужный вектор нормали:
glNormal3f (0, 0, -1);
Эту программу вы можете взять в качестве шаблона, чтобы поупражняться построениях. Проектировать системы из множества объектов без использования редакторов может оказаться трудным делом для новичков. Могу посоветовать воспользоваться приведенной выше процедурой построения осей текущей системы координат: обращайтесь к ней каждый раз, когда необходимо выяснить, "где я сейчас нахожусь".
Сплайны и поверхности Безье
Мы теперь можем без труда рисовать кубики, сферы, цилиндры и многие другие аналогичные
фигуры, но, конечно, этого недостаточно, и рано или поздно возникнет потребность
нарисовать поверхность произвольной формы. В этом разделе мы узнаем, как это
сделать.
Подход, предлагаемый библиотекой OpenGL для изображения криволинейных поверхностей,
традиционен для компьютерной графики: задаются координаты небольшого числа опорных
точек, определяющих вид искомой поверхности. В зависимости от способа расчета
опорные точки могут лежать наполучаемой поверхности, а могут и не располагаться
на ней.
Сглаживающие поверхности называются сплайнами. Есть много способов построения
сплайнов, из наиболее распространенных нас будут интересовать только два: кривые
Безье (Bezier curves, в некоторых книгах называются "сплайны Бежье")
и В-сплайны (base-splines, базовые сплайны). Изучение этой темы начнем с простейшего,
с двумерных кривых.
Операционная система располагает функциями GDI, позволяющими строить кривые
Безье.
В примере - проекте из подкаталога Ex40 - модуль OpenGL не используется, это
пример как раз на использование функций GDI. Он является модификацией одного
из проектов первой главы, но теперь рисуется не квадрат и круг, а кривая Безье
по четырем точкам - рис. 3. 27.
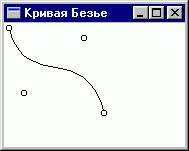
Рис. 3. 27. Функции GDI позволяют строить кривые Безье
вершины заданы в массиве четырех величин типа Tpoint, этот тип в модуле windows.
pas:
Const
Points: Array [0.. 3] of TPoint =
((x: 5; y: 5), (x: 20; y: 70), (x: 80; y: 15), (x: 100; y: 90));
Собственно рисование кривой состоит в вызове функции GDI polyBezier, первый аргумент которой - ссылка на контекст устройства, затем указывается массив опорных точек, последний аргумент - количество используемых точек:
PolyBezier (dc, Points, 4);
Построение для большей наглядности дополнено циклом, в котором окружностями визуализируются опорные точки:
For i: = 0 to 3 do
Ellipse (dc, Points [i]. x - 3, Points [i]. y - 3,
Points [i]. x + 3, Points [i]. y + 3);
В случае четырех опорных точек кривая всегда будет начинаться точно в первой
точке и приходить в последнюю точку. Если их переставить местами, вид кривой
не изменится, что не произойдет и если переставить местами вторую и третью опорные
точки. Опорные точки могут располагаться в пространстве произвольно, т e. не
требуется, чтобы они, например, равномерно располагались по интервалу. Если
необходимо продолжить кривую, добавляется по три точки для каждого последующего
сегмента.
Теперь посмотрим, как нарисовать кривую Безье, используя команды OpenGL. Откройте
проект из подкаталога Ex41. Получаемая кривая показана на рис. 3. 28.
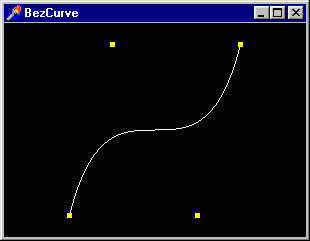
Рис. 3. 28. Кривая Безье, построенная с помощью функций библиотеки OpenGL
В обработчике создания формы задаются параметры так называемого одномерного вычислителя, и включается этот самый вычислитель:
glMaplf (GL_MAPl_VERTEX_3, 0. 0, 1. 0, 3, 4, @ctrlpoints);
glEnable (GL_MAPl_VERTEX_3);
Первый параметр команды glMapi - символическая константа, значение GL_MAPi_VERTEx_3
соответствует случаю, когда каждая контрольная точка представляет собой набор
трех вещественных чисел одинарной точности, т. e. координаты точки Значения
второго и третьего аргументов команды определяют конечные точки интервала предварительного
образа рассчитываемой кривой. Величины ноль и один для них являются обычно используемыми,
подробнее мы рассмотрим эти аргументы чуть ниже.
Четвертый параметр команды, "большой шаг", задает, сколько чисел содержится
в считываемой порции данных. Как говорится в документации, контрольные точки
могут содержаться в произвольных структурах данных, лишь бы их значения располагались
в памяти друг за другом.
Последние два параметра команды - число опорных точек и указатель на массив
опорных точек.
Для построения кривой можно использовать точки или отрезки' вместо команды,
задающей вершину, вызывается команда glEvalcoord, возвращающая координаты рассчитанной
кривой"
glBegln(GL__LINE_STRIP);
For i: = 0 to 30 do
glEvalCoordlf (i / 30. 0);
glEnd;
Аргумент команды - значение координаты u. В данном примере соединяются отрезками тридцать точек, равномерно расположенных на кривой Теперь выясним правила отображения интервала Если в этом примере третий параметр команды glMaplf задать равным двум, то на экране получим половину первоначальной кривой. Для получения полной кривой надо при воспроизведении взять интервал в два раза больший:
glBegln(GL_LINE_STRIP); For i: = 0 to 60 do
glEvalCoordlf(i / 30. 0); glEnd;
Если же этот параметр задать равным 0. 5, то при отображении интервала с u в пределах от нуля до единицы получаемая кривая не будет останавливаться на последней опорной точке, а экстраполироваться дальше. Если в этом нет необходимости, конечное значение параметра цикла надо взять равным 15 Чтобы действительно разобраться в подобных вопросах, надо обязательно попрактиковаться, посмотреть, какие кривые строятся для различных набо-Ров опорных точек. Здесь вам поможет проект из подкаталога Ex42, где cpe-Ди четырех опорных точек имеется одна выделенная. Клавишами управления курсором можно менять положение выделенной точки, при нажатии на Пробел выделенной становится следующая точка набора. Выделенная точка Рисуется красным Обратите внимание, что простой перерисовки окна при изменении в массиве опорных точек недостаточно, необходимо заново обратиться к командам, "заряжающим" вычислитель, чтобы пересчитать кривую:
If Key = VK_SPACE then begln
// выделенной становится следующая точка набора
selpoint: = selpoint + 1;
If selpoint > High (selpoint) then selpoint: = Low (selpoint);
InvalidateRect(Handle, nil, False);
end;
If Key = VK_LEFT then begln
// сдвигаем выделенную точку влево
ctrlpoints [selpoint, 0]: = ctrlpoints [selpoint, 0] - 0. 1;
// пересчитываем кривую по измененному массиву опорных точек
glMaplf(GL_MAPl_VERTEX_3, 0. 0, 1. 0, 3, 4, @ctrlpoints);
glEnable (GL_MAPl_VERTEX__3);
InvalidateRect(Handle, nil, False); // перерисовка окна
end;
С помощью этого примитивного редактора можно построить замысловатые фигуры и заодно получить представление о кривых Безье.
Замечание
Не получится расположить все четыре точки на кривой, если только это не линейная
функция.
С помощью команды glGetMapfv в любой момент можно получить полную информацию о текущих параметрах вычислителя. Не думаю, что вы часто будете обращаться к этой команде, но на всякий случай приведу пример на ее использование (проект из подкаталога Ex43). Клавишами <Insert> и <Delete> можно менять текущее значение параметра вычислителя u2, в заголовке окна выводятся значения u1 и u2. Эти значения приложение получает от OpenGL:
wrk: Array [0.. 1] of GLfloat;
begln
glGetMapfv (GL_MAPl_VERTEX_3, Caption: = FloatToStr (wrk[0]
GL_DOMAIN, @wrk); + ', ' + FloatToStr(wrk[l]);
Из файла справки вы можете узнать, как получить значения всех остальных параметров
вычислителя.
Построить кривую можно и другим способом. Посмотрим пример из подкаталога Ex44,
отличающийся от предыдущего примера на кривые Безье следующим: сразу после включения
вычислителя вызывается команда, строящая одномерную сетку, т. e. рассчитывающая
координаты набора точек на интервале:
glMapGridlf (30, 0, 1);
Первый аргумент - количество подинтервалов, далее задается интервал по координате u. После того как сетка построена, вывод ее осуществляется одной командой:
glEvalMeshl (GL_LINE, 0, 30);
Первый аргумент - режим воспроизведения, отрезками или точками, остальные аргументы
задают номера первой и последней точек рассчитанной сетки.
Получив представление о кривых, мы можем перейти к поверхностям Безье. Соответствующий
пример располагается в подкаталоге Ex45, а результат работы программы показан
на рис. 3. 29.
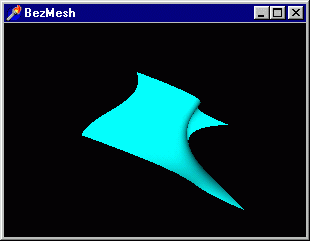
Рис. 3. 29. Классический пример на построение поверхности Безье
Массив опорных точек содержит координаты шестнадцати вершин. Работа программы начинается с установки параметров вычислителя:
glMap2f (GL_MAP2_VERTEX_3, 0, 1, 3, 4, 0, 1, 12, 4, @ctrlpoints);
glEnable (GL_MAP2_VERTEX_3);
glMapGrid2f (20, 0. 0, 1. 0, 20, 0. 0, 1. 0);
У команды glMap2f аргументов больше, чем у glMapif, но теперь нам легко понять
их смысл. Первый аргумент - константа, определяющая тип рассчитываемых величин,
в данном случае это координаты точек поверхности. Последний аргумент - указатель
на массив контрольных точек поверхности.
Второй и третий параметры задают преобразования по координате u поверхности.
Четвертый аргумент, как и в предыдущем случае, задает, сколько вещественных
чисел содержится в порции данных - здесь мы сообщаем, что каждая точка задана
тремя координатами. Пятый аргумент - количество точек в строке структуры, хранящей
данные.
Следующие четыре аргумента имеют смысл, аналогичный предыдущим четырем, но задают
параметры для второй координаты поверхности, координаты v. Значение восьмого
аргумента стало равно двенадцати путем пере- множения количества чисел, задающих
координаты одной вершины (3), на количество точек в строке массива (4).
После задания параметров вычислителя он включается вызовом команды giEnabie,
после чего вызывается одна из пары команд, позволяющих построить поверхность
- команда giMapGnd2f, рассчитывающая двумерную сетку. Первый и четвертый аргументы
этой команды определяют количество разбиений по каждой из двух координат поверхности,
остальные параметры имеют отношение к отображению интервалов.
Собственно изображение поверхности, двумерной сетки, осуществляется вызовом
второй команды из тандема:
glEvalMesh2 (GL_FILL, 0, 20, О, 20);
Первый аргумент команды задает режим воспроизведения, следующие две пары чисел
задают количество подинтервалов разбиения по каждой координате поверхности.
В примере мы берем по 20 разбиений, столько же, сколько задано в команде giMapGnd2f,
чтобы не выходить за пределы интервалов, но это не обязательно, можно брать
и больше.
Если смысл параметров, связанных с отображением интервалов, вам кажется не совсем
ясным, рекомендую вернуться к примеру по кривой Безье и еще раз его разобрать.
Замечу, что режим воспроизведения можно варьировать также с помощью Команды
glPolygonMode.
Обратите внимание, что в рассматриваемом примере используется режим автоматического
расчета нормалей к поверхности:
giEnabie (GL_AUTO_NORMAL);
Без этого режима поверхность выглядит невыразительно, но его использование
допускается только в случае поверхностей, рассчитываемых вычислителем.
В проекте введены два режима: один управляет тем, как строится поверхность -
сплошной или линиями. Второй режим задает, надо ли выводить опорные точки. Нажимая
на клавиши ввода и пробела, можно менять текущие значения этих режимов.
При нажатой кнопке мыши при движении курсора поверхность вращается по двум осям,
что позволяет хорошо рассмотреть ее с разных позиций Для осуществления этого
режима введен флаг, булевская переменная Down, которая принимает истинное значение
при удерживаемой кнопке мыши, и две вспомогательные переменные, связанные с
экранными координатами указателя.
В момент нажатия кнопки запоминаются координаты курсора; при движении курсора
сцена поворачивается по двум осям на угол, величина которого зависит от разницы
текущей и предыдущей координат курсора:
procedure TfrmGL.FormMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
If Down then begin // кнопка мыши нажата
glRotatef (X - wrkX, 0.0, 1.0, 0.0);// поворот по горизонтали экрана
glRotatef (Y - wrkY, 1.0, 0.0, 0.0);// поворот по вертикали экрана
InvalidateRect(Handle, nil, False); // перерисовать экран
wrkX := X; // запоминаем координаты курсора
wrkY := Y;
end;
end;
Но при изменении размеров окна система координат возвращается в первоначальное
положение.
Точно так же, как и в случае с кривой Безье, для воспроизведения поверхности
можно воспользоваться командой glEvalCoord2f. Отрезки строятся по вершинам,
предоставленным вычислителем:
9lBegm (GL_LINE_STRIP) ;
For i := 0 to 30 do For ] := 0 to 30 do
glEvalCoord2f (i / 30, j / 30);
glEnd;
Мы уже изучили множество параметров команды glEnable, задающей режимы воспроизведения
и, в частности, позволяющей использовать вычислители. Я должен обязательно привести
пример на команду, позволяющую определить, включен сейчас какой-либо режим или
вычислитель - команду glisEnabled. Ее аргумент - константа, символ определяемого
режима, а результат работы, согласно документации, имеет тип GLboolean. Мы знаем
о небольшой проблеме Delphi, связанной с этим типом, так что для вас не должно
стать откровением то, что обрабатывать возвращаемое значение мы будем как величину
булевского типа.
Приведу здесь простой пример, в котором до и после включения режима окрашивания
поверхностей выводится сообшение о том, доступен ли этот режим:
If glIsEnabled (GL_COLOR_MATERIAL) = TRUE
then ShowMessage ('COLOR_MATERIAL is enabled')
else ShowMessage ('COLOR_MATERIAL is disabled');
Соответствующий проект располагается в подкаталоге Ex47.
В этом разделе мы рассмотрели, как в OpenGL строятся кривые и поверхности Безье,
позже рассмотрим еще несколько примеров на эту тему.
NURBS-поверхности
Один из классов В-сплайнов, рациональные В-сплайны, задаваемые на неравномерной
сетке (Non-Uniform Rational B-Spline, NURBS), является стандартным для компьютерной
графики способом определения параметрических кривых и поверхностей.
Библиотека glu предоставляет набор команд, позволяющих использовать этот класс
поверхностей. Будем знакомиться с соответствующими командами непосредственно
на примерах и начнем с проекта из подкаталога Ex48, где строится NURBS-кривая
по тем же опорным точкам, что и в первом примере на кривую Безье. Вид получающейся
кривой тоже ничем не отличается от кривой, приведенной на рис. 3. 28.
Для работы с NURBS-поверхностями в библиотеке glu имеются переменные специального
типа, используемые для идентификации объектов:
theNurb: gluNurbsOb];
При создании окна объект, как обычно, создается:
theNurb: = gluNewNurbsRenderer;
А в конце работы приложения память, занимаемая объектом, высвобождается:
gluDeleteNurbsRenderer (theNurb);
Замечание
В отличие от quadric-объектов, удаленные NURBS-объекты действительно более недоступны
для использования.
Для манипулирования свойствами таких объектов предусмотрена специальная команда
библиотеки, в примере она используется для задания гладкости поверхности и режима
воспроизведения. Гладкость кривой или поверхности задается допуском дискретизации:
чем меньше это число, тем поверхность получается более гладкой:
gluNurbsProperty (theNurb, GLU_SAMPLING_TOLERANCE, 25. 0);
В отличие от других объектов, NURBS-поверхности рассчитываются каждый раз заново
при каждом построении. В этом легко убедиться, например, следующим образом:
увеличьте допуск дискретизации раз в десять и изменяйте размер окна. При каждой
перерисовке кривая получается разной.
Собственно построение кривой осуществляется следующей командой:
gluNurbsCurve (theNurb, 8, @curveKnots, 3, @ctrlpoints, 4, GL_MAPl_VERTEX_3 );
Первый аргумент - имя NURBS-объекта, вторым аргументом задается количество
параметрических узлов кривой, третий аргумент - указатель на массив, хранящий
значения этих узлов. Следующий параметр - смещение, т. e. сколько вещественных
чисел содержится в порции данных, далее следует указатель на массив опорных
точек. Последний аргумент равен порядку (степени) кривой плюс единица.
В документации указывается, что количество узлов должно равняться количеству
опорных точек плюс порядок кривой. Количество опорных точек достаточно взять
на единицу больше степени кривой, квадратичная кривая однозначно определяется
тремя точками, кубическая - четырьмя и т. д. Так что для построения квадратичной
кривой необходимо задавать шесть узлов:
gluNurbsCurve (theNurb, 6, 8curveKnots, 3,
@ctrlpoints, 3, GL_MAPl_VERTEX_3);
Значения параметрических узлов в массиве или другой структуре, хранящей Данные,
должны быть упорядочены по неубыванию, т. e. каждое значение не может быть меньше
предыдущего. Обычно значения первой половины Узлов берутся равными нулю, значения
второй половины задаются единичными, что соответствует неискаженной кривой,
строящейся на всем интервале от первой до последней опорной точки. прежде чем
мы сможем перейти к NURBS-поверхности, рекомендую самостоятельно поработать
с этим примером, посмотреть на вид кривой при различных значениях параметров.
Не забывайте о упорядоченности этих значе- ний, и приготовьтесь к тому, что
их набор не может быть совершенно произвольным: в некоторых ситуациях кривая
строиться не будет.
Теперь мы можем перейти к поверхностям, и начнем с проекта из подкаталога Ex49
- модификации классического примера на эту тему, в котором строится холмообразная
NURBS-поверхность (рис. 3. 30).
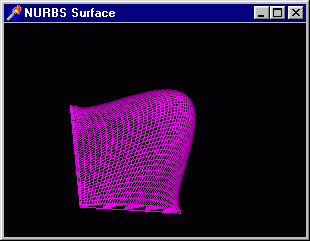
Рис. 3. 30. Классический пример на использование NURBS-поверхности
Первым делом замечу, что здесь появился новый для нас режим:
glEnable {GL_NORMALIZE);
Сделано это из-за того, что поверхность при построении масштабируется, и чтобы
автоматически рассчитанные нормали "не уплыли", и используется этот
режим.
Режим воспроизведения меняется по нажатию клавиши ввода, для его установки используется
та же команда gluNurbsProperty:
If solid
then gluNurbsProperty(theNurb, GLU_DISPLAY_MODE, GLU_FILL)
else gluNurbsProperty(theNurb, GLU_DISPLAY_MODE, GLU_OUTLINE_POLYGON);
Команда собственно построения заключена в специальные командные скобки:
gluBeglnSurface (theNurb); gluNurbsSurface (theNurb,
8, @knots,
8, @knots,
4 * 3,
3,
@ctrlpoxnts,
4, 4,
GL__MAP2_VERTEX_3);
gluEndSurface (theNurb);
В данном примере эти скобки не обязательны, поскольку они обрамляют единственную
команду.
Если вы внимательно разобрали примеры предыдущего раздела, то большинство параметров
команды gluNurbsSurface не должны вызывать вопросов, они аналогичны параметрам
команд для построения поверхности Безье.
Так, шестой и седьмой параметры задают "большой шаг" по каждой координате,
ассоциированной с поверхностью, т. e. сколько вещественных чисел содержится
в строке структуры данных и сколько вещественных чисел задают отдельную точку.
Восьмой параметр - адрес массива контрольных точек, а последним параметром задается
символическая константа, определяющая тип возвращаемых значений; в данном случае
ими являются трехмерные координаты вершин.
В примере задано шестнадцать контрольных точек, располагающихся равномерно по
координатам X и Y в пределах квадрата, третья координата для точек, лежащих
на границе квадрата, равна -3, для внутренних опорных точек эта координата равна
7. Таким способом массив заполняется для получения холмообразной поверхности.
Если по заданным опорным точкам построить поверхность Безье, то увидим точно
такой же холмик, как и в рассматриваемом примере.
Отличает NURBS-поверхности то, что параметризируемы. Так, предпоследние два
параметра задают степень (порядок) поверхности по координатам u и v. Задаваемое
число, как сказано в документации, должно быть на единицу больше требуемой степени.
Для поверхности, кубической по этим координатам, число должно равняться 4, как
в нашем примере. Порядок нельзя задавать совершенно произвольным, ниже мы разберем
имеющиеся ограничения.
Второй параметр команды - количество узлов в параметризации по и-на-правлению,
третьим параметром задается адрес массива, хранящего значения узлов. Третий
и четвертый параметры команды имеют аналогичный смысл, но для второго направления.
Массивы узлов должны заполняться значениями, упорядоченными по не-Убыванию.
Как сказано в файле справки, при заданных uknot_count и vknot_count количествах
узлов, uorder и vorder порядках количество опорных точек должно
ВНяться (uknot_count - uorder) x (vknot_count - vorder). Так что при изменении
порядка по координатам необходимо подбирать и все остальные параметры поверхности.
если вы хотите подробнее узнать о параметризации и ее параметрах, то обратитесь
к литературе с подробным изложением теории NURBS-поверхностей.
Вданном примере используется один массив для задания узлов по обоим направлениям,
а в проекте из подкаталога Ex50 используется два отдельных массива - для каждой
координаты задаются свои значения узлов Поверхность строится не на всем интервале,
а на части его, т. е. происходит подобие отсечения.
Чаще всего используются "кубические" NURBS-поверхности. Для иллюстрации
построения поверхностей других порядков предназначен проекч из подкаталога Ех51,
где берется "квадратичная" поверхность
Библиотека glu предоставляет также набор команд для вырезки кусков NURBS-поверхностей.
Примером служит проект из подкаталога Ех52 Опорные точки поверхности располагаются
в пространстве случайно, а за)ем из поверхности вырезается звездочка - рис.
3.31.
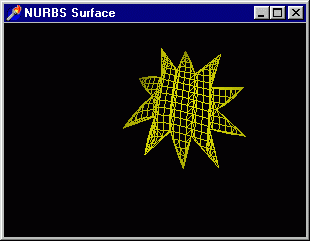
Рис. 3.31 Команды библиотеки glu позволяют строить невыпуклые многоугольники
Для хранения точек на границе вырезаемой области - звездочки - введен массив:
trim: Array [Q..2Q, 0..1] of GLfloat;
Массив заполняется координатами точек, лежащих поочередно на двух вложенных окружностях:
procedure InitTrim;
var
i: Integer;
begin
Eor i := 0 to 20 do
If Odd(i) then begin // нечетные точки - на внешней окружности
trim [i, 0] := 0.5 " cos (i * Pi / 10) + 0.5;
trim [i, 1] := 0.5 * sin (i * Pi / 10) + 0.5;
end
else begin // четные точки - на внутренней окружности
trim (if 0] := 0.25 * cos (i * Pi / 10) + 0.5;
trim [i, 1] := 0.25 * sin (i * Pi / 10) + 0.5;
end;
end;
Внутри операторных скобок построения NURBS-поверхности вслед за командой giuNurbsSurface задаем область вырезки:
gluBeginTrirr (theNurb) ;
gluPwlCurve (theNurb, 21, Qtnm, 2, GLU_MAP1_TRIM__21 ;
gluFndlrim (theNurb);
При задании области вырезки используются опять-таки специальные командные скобки,
собственно область вырезки задается командой gluPwlCurve. Команда задает замкнутую
кусочно-линейную кривую, часть NURBS-поверхности, не вошедшая внутрь этой области,
не воспроизводится. Второй аргумент - количество точек Гранины, третий - адрес
массива этих точек, четвертым параметром является символьная константа, задающая
тип вырезки.
В примере при каждом нажатии пробела вызывается процедура инициализации поверхности,
так что вид звездочки каждый раз получается разным,
случайным.
Следующий пример (подка!алог Ех53) также иллюстрирует вырезку NURBS-поверхности
(рис. 3 32).
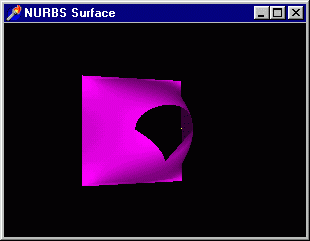
Рис. 3.32. Вырезка внутри NURBS-поверхности
Здесь вырезается внутренняя область поверхности, для чего задаются две линии,
связанные с вырезкой:
gluBeginTrm (theNurb);
gluPwlCurve (theNurb, 5, SedgePt, 2, GLU_MAPl_TRIM_2);
gluEndTrim (theNurb);
gluBeginlrim (theNurb);
gluNurbsCurve (theNurb, 8, @curvcKnots, 2,
@curvo?t, 4, GLU_MAPl_TRIM_2);
gluPwlCurve (theNurb, 3, PpwlPt, 2, GLL_MAP1_TRIM_2) ;
SluEnaTrim (theNurb);
Первая линия охватывает весь интервал по обеим координатам поверхности, в массиве
указаны точки границы по часовой стрелке:
edgePt : Array [0..4, 0..1] of GLfloat = ((0.0, 0.0), (1.0, 0.0),
(1.0, 1.0), (0.0, 1.0), (0.0, 0.0));
Теперь следующая область вырезки ограничивает внутреннюю вырезаемую область.
В примере эта область состоит из двух кривых; если это усложняет понимание программы,
строку с вызовом giuNurbsCurve можете удалить, а массив граничных точек дополните
замыкающей точкой:
pwlPt : Array [0..3, 0..1] of GLfloat = ((0.75, 0.5), (0.5, 0.25),
(0.25, 0.5), (0.75, 0.5));
Как и во многих предыдущих примерах, по нажатию пробела визуализируются опорные точки поверхности. Этот пример прекрасно иллюстрирует, как можно манипулировать параметрами NURBS-поверхности для выявления преимуществ параметризации. Обратите внимание, что опорные точки заданы только для одной половины воспроизводимой симметричной фигуры
Дисплейные списки
В этом разделе мы познакомимся с одним из важнейших понятий OpenGL Дисплейные
списки представляют собой последовательность команд, запо-
минаемых для последующего вызова. Они подобны подпрограммам и являются удобным
средством для кодирования больших систем со сложной иерархией.
Знакомство начнем с проекта из подкаталога Ех55, классического примера на эту
тему Работа приложения особо не впечатляет: рисуется десять треугольников и
отрезок (рис 3.33).

Рис. 3.33. Первый пример на использование дисплейных списков
В начале работы вызывается процедура инициализации, где создается (описывается) дисплейный список:
const
listName : GLUint = 1; // идентификатор списка
procedure init;
begin
glNewList (listName, GL_CCMPILE}; // начало описания списка
glColor3f (1.0, 0.0, 0.0);
glBegin (GL_TRIANGLES);
glVertex2f (0.0, 0.0);
glVertex2f (1.0, 0.0);
glVertex2f (0.0, 1.0);
glEnd;
glTranslatef (1.5, 0.0, 0.0);
glEndList; // конец описания списка
end;
Описание списка начинается с вызова команды giNewList, первым аргументом которой
является целочисленный идентификатор - имя списка (в примере именем служит константа).
Вторым аргументом команды является символическая константа; здесь мы указываем
системе OpenGL на то, что список компилируется для возможного последующего использования.
Все следующие до glEndList команды OpenGL и образуют дисплейный список, единую
последовательность.
В данном примере в списке задается красный цвет примитивов, далее сле-Дуют команды
для построения одного треугольника, заканчивается список Переносом системы координат
по оси X.
В коде воспроизведения кадра цвет примитивов задается зеленым, затем десять
раз вызывается описанный список.
glColor3f (0.0, 1.0, 0.0); // текущий цвет - зеленый
glPushMatrix; // запомнили систему координат
For i := 0 to 9 do // десять раз вызывается список с именем
glCallList (listName);
drawLine; // построить отрезок
glPopMatnx; // вернулись в запоганенную систему координат
Списки вызываются командой gl call List, единственным аргументом которой является
идентификатор вызываемого списка.
В примере после каждого вызова списка номер один система координат смещается,
поэтому на экране получается ряд треугольников, а отрезок рисуется вслед за
последним треугольником. Хотя цвет примитивов задается зеленым, в списке он
переустанавливается в красный, поэтому отрезок рисуется именно таким цветом.
Новички часто путаются, считая дисплейные списки полной аналогией подпрограмм.
Отличает списки от подпрограмм то, что списки не имеют параметров, команды при
вызове списка действуют точно так же, как и при создании списка. Если при описании
списка используются переменные, то при вызове списка значения этих переменных
никак не используются. Впрочем, ряд команд, помещенных в список, при вызове
будут отрабатываться каждый раз заново, в документации приведен список таких
команд.
Замечание
Я много раз встречал утверждение, что использование списков эффективно по причине
того, что компиляция их приводит к более быстрому выполнению - в списке не запоминаются
промежуточные команды. Если это и так, то ощутить "на глаз" ускорение
работы приложения при использовании дисплейных списков как-то не получается.
Тем не менее, я настоятельно рекомендую их использовать, это приводит к повышению
читабельности и упрощению кода.
По окончании работы память, занятую списками, необходимо освобождать, как это
делается в этом примере:
qlDeleteLists (listNamer 1);
Первый аргумент команды - имя первого удаляемого списка, второй параметр -
количество удаляемых списков. Удаляются все списки, следующие за указанным.
Стоит напомнить, что удалять списки необходимо до освобождения контекста воспроизведения.
В продолжение темы рассмотрим проект из подкаталога Ех56, Результат работы приложения
приведен на рис. 3.34.

Рис 3.34. В этом примере цветовые настройки при использовании списка
не сбиваются
Пример иллюстрирует несколько аспектов, связанных с дисплейными списками.
Во-первых, это использование команды gicenLists, генерирующей имя для списка.
В примере идентификатором используемого списка является переменная, а не константа.
Перед описанием списка значение этой переменной подбирается системой OpenGL
среди незанятых на текущий момент значений:
]_i=,-cName := glGenLists (1);
То есть вы можете и не затрачивать усилий на то, чтобы самому следить за именами
используемых списков, а полностью положиться в этом вопросе на OpenGL. Это особенно
удобно при интенсивной работе со списками, формируемыми в программе динамически.
Во-вторых, обратите внимание, что каждый вызов списка не портиг текущие цветовые
настройки. Корректность работы обеспечивается использованием пары новых для
нас команд: glPushAttna
glPopAttrib:
glNewList (listName, GL_COMPILE);
glPushAttrib (GL_CURRENT_BIT); // запомнили текущие атрибуты цвета
glColor3fv (@color_vector); // установили нужный цвет
glBegin (GL_TRIANGLES); // отдельный треугольник
glVertex2f (0.0, 0.0);
glVertex2f (1.0, 0.0);
glVertex2f (0.0, 1.0) ;
glEnd;
glTranslatef (1.57 0.0, 0.0);
glPopAttrib; // восстановили запомненные настройки
glSnaList;
Аналогично командам сохранения и восстановления системы координат, эта пара
команд позволяет запоминать в отдельном стеке текущие настройки и возвращаться
к ним. Аргумент команды glPushAttrib - символическая константа - задает, какие
атрибуты будут запоминаться (значение в примере соответствует запоминанию цветовых
настроек). Из документации можно Узнать, что существует целое множество возможных
констант для этой команды; если вам покажется сложным разбираться со всеми ними,
то пользуйтесь универсальной константой GLJ\LLJYTTRIB_BITS, в этом случае в
стеке атрибутов запомнятся разом все текущие установки.
При перерисовке окна текущая система координат запоминается перед вы-Зовом списков
и восстанавливается перед прорисовкой отрезка:
glPushMatrix;
For i := 0 to 9 do
glCallList (listName);
glPopMatrix;
drawLine;
Поэтому в примере отрезок рисуется поверх ряда треугольников.
Следующий пример, проект из подкаталога Ех57, является очень простой иллюстрацией
на использование команды giisList, позволяющей узнать, существует ли в данный
момент список с заданным именем. Аргумент команды - имя искомого списка, возвращает
команда величину типа GLbooiean (как всегда в таких случаях, в Delphi обрабатываем
результа! как булевскую переменную):
If giisList (listName)
then ShowMessage ('Список с именем listName существует')
else ShowMessage ('Списка с именем listName не существует');
Теперь перейдем к проекту из подкаталога Ех58. Результат работы программы отличается от первого примера этого раздела только тем, что рисуется восемь треугольников вместо десяти, но суть примера не в этом: здесь иллюстрируется то, что при описании списка можно использовать вызов других списков. В примере описано три списка:
const // идентификаторы используемых списков
listNamel : GLUint = 1;
listName2 : GLUint = 2;
listName3 : GLUint = 3;
procedure unit;
var
i : GLuint;
begin
glNewList (listNamel, GL_COMPILE); // список 1 - отдельный треугольник
glColorSf (1.0, 0.0, 0.0);
glBegin (GL_TRIANGLES);
glVertex2f (0.0, 0.0);
glVertex2f (1,0, 0.0);
glVertex2f (0.0, 1.0);
glEnd;
glTranslatef (1.5, 0.0, 0.0);
glEndList;
glNewList (listName2, GL_COMPILE); // список 2 - четыре треугольника
For i := 0 to 3 do
glCallList (listNamel); // вызывается прежде описанный список 1
glEndList;
glNewList <listName3, GL_COMPILE); // список З - четыре треугольника
glCallList (listName21; // вызывается прежде описанный список 2
glEndList;
end;
Второй и третий списки используют прежде описанные списки, но gicaiiList относится
к тем командам, которые, будучи помещенными в список, при выполнении его выполняются
независимо от дисплейного режима, т. е. не компилируются. Так что в этом примере
результат не изменится, если описания второго и третьего списков поменять местами.
В примере введен массив, содержащий имена двух списков.
const list : Array [0..1] of GLUint = (2, 3);
Этот массив используется при воспроизведении кадра в команде, позволяющей вызвать сразу несколько дисплейных списков:
glCallLists (2, GL_INT, @list);
Первый аргумент команды - количество вызываемых списков, второй аргумент указывает
смещение, третий аргумент - указатель на структуру, содержащую имена вызываемых
списков. Смещение задано согласно описанию используемого массива из указанного
в файле справки списка возможных констант.
В примере вначале вызывается список с именем 2 и строятся первые четыре треугольника.
Затем вызывается список с именем 3, который состоит во вторичном вызове списка
номер 2.
Замечание
Подобный прием может показаться малополезным, но важно хорошо разобраться в
этом и следующем примерах, поскольку используемые в них команды будут применяться
в дальнейшем для вывода текста.
Последний пример этого раздела, проект из подкаталога Ех59, по своему Функциональному
действию ничем не отличается от предыдущего, однако Для нас в нем интересна
новая команда - giListBase. Смысл ее очень прост - она задает базовое смещение
для имен вызываемых списков.
В примере это смещение задано единичным:
3U,istBase (1);
А массив имен вызываемых списков содержит значения на единицу меньше, чем в предыдущем примере:
Ust : Array [0..1] of GLUint = (1, 2);
При вызове списков командой glCallLists к их именам
прибавляется заданное смещение.
Tess-обьекты
Мозаичные (tesselated - мозаичный) объекты являются последним нововведением
библиотеки glu, предназначены они для упрощения построений нс-выпуклых многоугольников.
После того как мы изучили основные объекты библиотеки glu, нам будет несложно
освоиться с собственно tess-объектами.
Рабога с ними в DeIplhi сопряжена с трудностями, возникающими из-за того, что
раздел заголовочного файла, посвященный этим объектам, содержит несколько ошибок.
Рис. 3. 39 демонстрирует работу примера проекта, расположенного в под каталоге
Ex60.
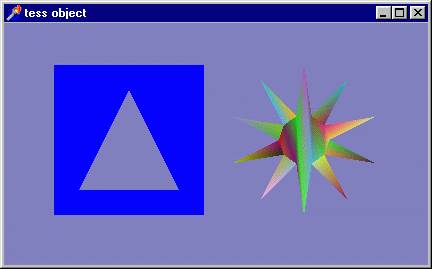
Рис. 3. 35. Tess-объекты можно использовать для тех же целей, что и NURBS-поверхности
В программе определен особый тип для хранения координат одной точки:
type
TVector = Array [Q.. 2] of GLdouble;
Для уверенной работы команд данного раздела следует использовать именно гип
удвоенной точности.
В процедуре инициализации описана переменная специального типа, введенного для
работы с мозаичными объектами. Она инициализируется приблизительно так же, как
другие объекты библиотеки glu, но, конечно, другой командой:
var
tobj: gluTesselator;
...
tobj: = gluNewTess;
Теперь посмотрим, как подготавливается список для левой фигуры, квадрата с
треугольным отверстием внутри.
С помощью команды gluTessCallback задаются адреса процедур, вызываемых на различных
этапах рисования tess-объекта, например:
gluTessCallback{totrj, GLU_TESS_BEGIN, @glBegln); //начало рисования
При начале рисования объекта мы не планируем особых манипуляций, поэтому просто
передаем адрес процедуры qlBegln.
Если же нам по сценарию потребуется выполнить какие-то дополнительные действия,
необходимо описать пользовательскую несвязанную (не являющуюся частью описания
класса) процедуру, обязательно указав ключевое слово stdCall, и передавать адрес
эгой процедуры.
Синтаксис описания подобных процедур описан в справке по команде glutessCallback.
Например, если мы хотим, чтобы перед воспроизведением примитива подавался бы
звуковой сигнал, необходимо вызвать следующую процедуру:
procedure beglnCalIback(which GLenum); stdcall;
begln
MessageBeep (MB_OK);
glBegln(which);
end;
...
gluTessCallback(tobj, GLU_TESS_BEGIN, @ BeglnCallback);
Имя процедуры безразлично, но аргументы ее должны задаваться строго по указаниям,
содержащимся в документации.
Внимательно посмотрите на следующие две строки кода:
gluTessCallback (tobj, GLU_TESS_VERTEX, @glVertexJdv); // вершина
glutessCallback(tobj, GLU_TESS_SND, 3glEnd); // конец рисования
To есть при обработке отдельной вершины и в конце рисования примитивов также
не будет выполняться чего-то необычного.
Для диагностики ошибок, возникающих при работе с tess-объектами, ис-Пользуем
пользовательскую процедуру:
procedure errorCallback(errorCode: GLenum); stdcall;
begln
ShowMessage (gluErrorString(errorCode));
end;
...
gluTessCallback(tobj, GLU_TESS_ERROR, @errorCallback]; //ошибка
Команда gluErrorstring возвращает строку с описанием возникшей ошибки. Описание
ошибки выдается на русском языке (на языке локализации операционной системы),
так что с диагностикой проблем не будет.
Координаты вершин квадрата и треугольника вырезки хранятся в структурах, единицей
данных которых должна быть тройка вещественных чисел:
const
rect: Array [0.. 3] of TVector = ((50. 0, 50. 0, 0. 0),
(200. 0, 50. 0, 0. 0),
(200. 0, 200. 0, 0. 0),
(50. 0, 200. 0, 0. 0));
tri: Array[0.. 2] ofTVector= ((75. 0, 75. 0, 0. 0),
(125. 0, 175. 0, 0. 0),
(175. 0, 75. 0, 0. 0));
Наша фигура строится приблизительно по таким же принципам, что и в примере на вырезку в NURBS-поверхности:
glNewList(l, GL_COMPILE);
glColor3f(0. 0, 0. 0, 1-0); //цвет-синий
gluTessBeglnPolygon (tobj, nil); // начался tess-многоугольник
gluTessBeglnContour(tobj); // внешний контур - квадрат
gluTessVertex(tobj, @rect[0], @rect[Q]); // вершиныквадрата
gluTessVertex(tobj, @rect[l], @rect[l]);
gluTessVertex(tob], @rect[2], @rect[2]);
gluTessVertex(tobj, @rect[3], @rect[3]);
gluTessEndContour (tobj);
glutessBeglnContour(tobj); // следующие контуры задают вырезки
gluTessVertex(tobj, @tri[0], @tri[0]); // треугольник
gluTessVertex(tobi, @tn[l], @tri[l]);
gluTessVertex(tobj, @tn[2], @tri[2]);
gluTessEndContour(tobj);
gluTessEndPolygon(tobj); // закончили с tess-многоугольником
glEndList;
При перерисовке окна просто вызывается список с именем 1.
После того как список описан, tess-объект можно удалить, это делается в конце
процедуры инициализации:
gluDeleteTess(tobj);
Замечание
Обратите внимание: при вызове списка сами объекты библиотеки glu уже не используются.
Точно так же вы можете удалять quadric-объекгы сразу после описания всех списков,
использующих их.
Надеюсь, с первой фигурой вам все понятно, и мы можем перейти ко второй фигуре,
звездочке.
Здесь для наглядности перед вызовом каждой вершины текущий цвет меняется, для
чего описана специальная процедура, адрес которой задается вызовом команды gluTessCallback:
procedure vertexCallback (vertex: Pointer); stdcall;
begln
glColor3f (random, random, random);
glVertex3dv (vertex);
end;
...
gluTessCallback{tobj, GLU_TESS_VERTEX, @vertexcallback);
Массив, хранящий координаты вершин звездочки, заполняется приблизительно так же, как в одном из предыдущих примеров на NURBS-no-верхность. Многоугольник второго списка состоит из единственного контура. Перечисляем вершины, хранящиеся в массиве:
glNewList(2, GL_COMPILE);
gluTessBeglnPolygon (tobj, nil);
gluTessBeglnContour(tobj}; For i: = 0 to 20 do
gluTessVertex(tobj, @star [i], @star [i]);
gluTessEndContour (tobj);
gluTessEndPolygon (tob]);
glEndList;
Прототип одной из используемых команд мне пришлось переписать:
procedure gluTessBeginPolygon (tess: GLUtesselator; polygon_data:
Pointer); stdcall; external GLU32;
To, что записано в стандартном заголовочном файле, расходится с документацией
и приводит к ошибке.
Мы рассмотрели простейший пример на использование tess-объектов, и надеюсь,
вы смогли оценить, как удобно теперь становится рисовать невыпуклые многоугольники.
В качестве исследования можете задать контурный режим воспроизведения многоугольников,
чтобы увидеть, как строятся получающиеся фигуры. Приведу еще несколько примеров
на мозаичные объекгы. Подкаталог Ex6l содержит проект, где строится объект в
виде звездочки (рис. 3. 36)

Рис. 3. 36. Звездочка построена по координагам пяти вершин
На первый взгляд вам может показаться, что этот пример проще предылу-щего,
однако это не так: звездочка задана координатами пяти вершин, перечисляемых
в том порядке, в котором обычно дети рисуют пятиконечные звезды. Мне пришлось
изрядно потрудиться, чтобы этот пример заработал.
Если попытаться в предыдущем примере задать вершины звезды именно по такому
принципу, мы получим сообщение об ошибке "требуется составной ответный
вызов" (на русском). To есть серверу надо подсказать, как обрабатывать
ситуации с пересечениями границ контура.
Почерпнув всю требуемую информацию из файла справки, я написал следующую процедуру
и задал ее адрес для вызова обработчика пересечения:
gluTessCallback(tODJ, GLU_TESS_COMBTNE, @combineCallback;;
Для того чтобы заполнить внутренности фигуры, я использовал команду. позволяющую определять свойства мозаичного объекта:
gluTessPiOpertyiCobj, GLU_TESS_WINDING R'JLE, GLU_TESS_WINDING POSlTIVE);
Обратите внимание, что значение первой символической константы в программе
переопределено, в файле opengl. pas это значение задано неверно.
Предоставляю вам еще один пример на эту тему, проект из подкаталога Ex62. Не
стану разбирать этот пример, чтобы не испугать начинающих Если он вам покажется
трудным, можете отложить его подробное изучение на потом - до того момента,
когда вы будете чувствовать себя с OpenGL совсем уверенно.
По ходу подготовки этого примера я обнаружил массу ошибок все в том же заголовочном
файле, так что мне самому он дался очень тяжело.
Таймеры и потоки
В этом разделе мы познакомимся с различными способами создания анимации. При
этом нам придется сосредоточиться на вопросах, больше связанных с операционной
системой, чем с OpenGL.
Для самых простейших задач вполне подходит использование обычного таймера Delphi.
Посмотрим проект из подкаталога Ex63. Это немного модифицированный пример второй
главы, в котором вокруг курсора рисовалось облачко отрезков. Теперь это облачко
постоянно меняется так, что картинка еще более напоминает бенгальский огонь.
Первое изменение в проекте заключается в том, что на форме появился таймер,
обработчик которого заключается в том, что десять раз в секунду окно перерисовывается.
При каждой перерисовке окна вокруг курсора рисуется множество отрезков со случайными
координатами конца.
Важно обратить внимание на действия, позволяющие ускорить работу приложения.
Вместо традиционного для проектов De]phi вызова метода Refresn окно перерисовывается
вызовом функции API (мы уже убедились, насколько это значимо):
procedure TfrmGL. TimerlTimer{Sender: TObject};
begln
lnvalidateRect(Handle, nil, False);
end;
Цвет окна формы я намеренно задал ярко-синим, чтобы проиллюстрировать, как
важно в таких приложениях бороться за каждую миллисекунду. Если в обработчике
таймера поставить Refresh, то при каждой перерисовке окно мерцает, по нему пробегают
синие полосы Впрочем, чожет случиться и так, что на вашем компьютере такие эффекты
не возникают, тут многое зависит от характеристик "железа".
Также для ускорения работы в этом примере вместо canvas. Handle используется
явно полученная ссылка на контекст устройства.
Код перерисовки окна максимально сокращен, в нем оставлено только то, что не
переносится в другие обработчики. Включение режима штриховки и задание области
вывода перемещены в обработчики onCreate и onResize Формы, соответственно. В
таких приложениях также желательно использовать перехватчик сообщения WM_pAiNT
вместо обработчика onPaint. Это сделано в следующем примере, проекте из подкаталога
Ex64, в котором экране двигаются по кругу шесть кубиков (рис. 3. 37).

Рис. 3. 37. При работе программы кубики вращаются по кругу
Положения центров кубиков хранятся во вспомогательных массивах, заполняемых при начале работы приложения синусами и косинусами:
For i: = 0 to 5 do begln
wrkX [i] : = sin (Pi / 3 * i);
wrkY [i] : = соз (Pi / 3 * j);
end;
Поворот всей системы с течением времени обеспечивается тем, что в обработчике таймера значение переменной, связанной с углом поворота, увеличивается, после чего экран перерисовывается:
Angle: = Angle + 1; // значение угла изменяется каждый "тик"
If Angle >= 60. 0 then Angle: = 0. 0;
InvalidateRect(Handle, nil, False);
Ядро кода воспроизведения кадра выглядит так:
glPushMatrix; // запомнили начальную систему координат
glRotatef(Angle, 0. 0, 0. 0, 1. 0); // поворот системы на угол
Angle по 2 {Цикл рисования шести кубиков}
For i: = С to 5 do begln glPushMatrix; // запомнили систему координат
glTranslatef(wrkX [i], wrkY [i], 0. 0); // перенос системы координат
glRotatef(-60 * i, 0. 0, 0. 0, 1. 0); // поворот кубика
glutSolidCube (0. 5);
glPopMatrix; end;
// рисуем кубик
// вернулись в точку
glPopMatrix; // вернулись в первоначальную систему координат
Занятный результат получается, если поменять местами первые две строки этого кода, обязательно посмотрите, к чему это приведет.
Замечание
Приведет это к тому, что кубики будут вращаться все быстрее и быстрее: теперь
они при каждом тике таймера поворачиваются на все более увеличивающийся угол
Angle относительно предыдущего положения Можно использовать более оптимальный
прием в подобных примерах не использовать управляющую переменную (здесь это
Angle}, не использовать команды glPushmatrix и glPopMatrix, а код кадра начинать
с поворота на угол, константу. С точки зрения скорости это оптимально, но может
нарушать сценарий кадра' ведь при изменении размеров окна мы принудительно возвращаем
объекты сцены в первоначальную систему координат, и кубики резко дергаются.
Использование системного таймера является самым простым решением задачи, но
имеет очевидные недостатки. На маломощных компьютерах уже этот пример выводит
кадры рывками, а если количество объектов перевалит за два десятка, то удовлетворительную
скорость воспроизведения можно будет получить только на очень хороших машинах.
Следующий пример, проект из подкаталога Ex65, является продолжением предыдущего,
здесь рисуется пятьдесят параллелепипедов (рис. 3. 38).

Рис. 3. 38. Эту систему мы возьмем в качестве тестовой для сравнения методов создания анимации
Вся система вращается по двум осям, по оси Y вращение происходит с удвоенной скоростью:
glRotatef(2 * Angle, 0. 0, 1. 0, O. 0}; // поворот по ось Y
glRotatef(Angle, 0. 0, 0. 0, 1. 0}; // поворот по оси Z
Интервал таймера я задал равным 50 миллисекунд, т. e. экран должен обновляться
двадцать раз в секунду. Попробуем выяснить, сколько кадров В секунду выводится
в действительности.
Это делается в проекте из подкаталога Ex66. Введены переменные, счетчики кадров
и количество кадров в секунду:
newCount, frameCount, lastCount: LongInt;
fpsRate: GLfloat;
При запуске приложения инициализируем значения:
lastCount: = GetTickCount;
frameCount: = 0; ;
Функиия API GetTickCount возвращает количество миллисекунд, прошедших с начала
сеанса работы операционной системы
При воспроизведении кадра определяем, прошла ли очередная секунда, и вычисляем
крличество кадров, выведенных за эту секунду:
newCount: = GetTickCount; // текущее условное время
Inc(frameCount); // увеличиваем счетчик калроя
If (newCount - lastCount) > 1000 then begln // прошла секунда
// определяем количество выведенных кадров
fpsRate: = frameCount * 1000 / (newCount - lastCounU;
// выводим в заголовке количество кадров
Caption: = 'FPS - ' + FloatToStr {fpsRate);
lastCount: = newCount; // запоминаем текущее время
frameCount: - 0; // обнуляем счетчик кадров
end;
Получающееся количество воспроизведенных кадров в секунду зависит от многих
факторов, в первую очередь, конечно, от характеристик компьютера, и я не могу
предсказать, какую цифру получите именно вы. Будет совсем неплохо, если эта
цифра будет в районе двадцати.
Но если задаться целью увеличить скорость работы этого примера, то выяснится,
что сделать это будет невозможно, независимо от характеристик компьютера. Сколь
бы малым не задавать интервал таймера, выдаваемая частота воспроизведения не
изменится, системный таймер в принципе не способен обрабатывать тики с интервалом
менее пятидесяти миллисекунд Еще один недостаток такого подхода состоит в том,
что если обработчик тика таймера не успевает отработать все действия за положенный
интервал времени, то последующие вызовы этого обработчика становятся в очередь.
Это приводит к тому, что приложение работает с разной скоростью на различных
компьютерах.
Мы не будем опускать руки, а поишем другие способы анимации, благо их существует
несколько. Рассмотрим еще один из этих способов (я его нахожу привлекательным),
состоящий в использовании модуля MMSystem (Multimedia System). Мультимедийный
таймер позволяет обрабатывать события с любой частотой, настолько часто, насколько
это позволяют сделать ресурсы компьютера.
Посмотрим на соответствующий пример - проект из подкаталога Ex67 Здесь рисуются
все те же пятьдесят параллелепипедов, но часгота смены кадров существенно выше.
Список подключаемых модулей в секции implementation дополнился модулем MMSystem:
uses DGLUT, MMSystem;
Мультимедийный таймер также нуждается в идентификаторе, как и обычный системный, описываем его в разделе private класса формы:
TimerId: uint;
А вот процедура, обрабатывающая тик таймера, не может являться частью класса:
procedure TimeProc (uTimerID, uMessage: UINT; dwUser, dwl, dw2: DWORD; stdcall;
// значение угла изменяется каждый "тик"
With frmGL do begln
Angle: = Angle + 0. 1;
If Angle >= 360. 0 then Angle: - 0. 0;
InvalidateRect (HandJe, nil, False);
end;
end;
При создании окна таймер запускается специальной функцией API:
TimerID: = time SetSvent (2, 0, @TimeProc, 0, TIME_PERTGDIC);
По окончании работы приложения таймер необходимо остановить; если это не сделать, то работа операционной системы будет заметно замедляться;
tirreKillEvent (TimerID);
Самым важным в этой цепочке действий является, конечно, команда установки таймера, timeSetEvent. Первый аргумент команды - интервал таймера в миллисекундах. Вгорой аргумент - разрешение таймера, т. e. количество миллисекунд, ограничивающее время на отработку каждого тика таймера. Есди это число задано нулем, как в нашем примере, то обработка таймера Должна происходить с максимальной точностью.
Замечание
В документации рекомендуется задавать ненулевое значение для уменьшения системных
потерь
Следующий параметр - адрес функции, ответственной за обработку каждого тика.
Четвертый параметр редко используется, им являются задаваемые пользователем
данные возврата Последним параметром является символи ческая константа, при
этом значение TIME_PERIODIC соответствует обычному поведению таймера.
Итак, в примере каждые две миллисекунды наращивается угол поворота системы и
перерисовывается экран.
Конечно, за две миллисекунды экран не будет перерисован, однако те кадры, которые
компьютер не успевает воспроизвести, не будут накапливаться. При использовании
мультимедийного таймера сравнительно легко планировать поведение приложения
во времени: на любом компьютере и в любой ситуации система будет вращаться с
приблизительно одинаковой скоростью, просто на маломощных компьютерах повороты
будут рывками В продолжение темы посмотрите проект из подкаталога Ex68, где
все тот же мультфильм рисуется на поверхности рабочего стола, подобно экранным
заставкам. Во второй главе мы уже рассматривали похожий пример, здесь добавлена
анимация, а команда glviewPort удалена, чтобы не ограничивать область вывода
размерами окна приложения.
Замечание
Напоминаю, что такой подход срабатывает не на каждой карте
Наиболее распространенным способом построения анимационных приложений является
использование фоновой обработки, альтернативы таймерам. Разберем, как это делается.
В Delphi событие onidle объекта Application соответствует режиму ожидания приложением
сообщений. Все, что мы поместим в обработчике этого события, будет выполняться
приложением беспрерывно, пока оно находится в режиме ожидания.
Переходим к примеру, проекту из подкаталога Ex69. Сценарий приложения не меняем,
чтобы можно было сравнить различные способы. Отличает пример то, что в нем отсутствуют
какие-либо таймеры; код, связанный с анимацией, перешел в пользовательскую процедуру:
procedure TfrmGL. Idle (Sender: TObject; var Done: boolean);
begln
With frmGL do begln
Angle: = Angle + 0. 1;
If Angle >= З60. 0 then Angle: = 0. 0;
Done: = False; // обработка завершена
InvalidateRect{Handle, nil. False);
end;
end;
Второй параметр Done используется для того, чтобы сообщить системе, требуется
ли дальнейшая обработка в состоянии простоя, или алгоритм завершен. Обычно дается
False, чтобы не вызывать функцию WaitMessage.
При создании окна устанавливаем обработчик события onidle объекта Application:
Application. OnIdle: = Idle;
Вот и все необходимые действия, можете запустить приложение и сравнить этот метод с предыдущим.
Замечание
При тестировании на компьютерах, оснащенных ускорителем, этот способ дал наивысший
показатель при условии обычной загруженности системы На компьютере без акселератора
цифры должны получиться одинаковые, однако примеры с мультимедийным таймером
выглядят поживее
При использовании последнего способа у нас нет никакого контроля над выполнением
кода, есть только весьма приблизительное представление о том. сколько времени
будет затрачено на его выполнение. Скорость работы приложения в этом случае
полностью зависит от загруженности системы, другие приложения могут с легкостью
отнимать ресурсы, и тогда работа нашего приложения замедлится, Запустиге одновременно
приложения, coответствующие мультимедийному таймеру и фоновой обработке Активное
приложение будет генерировать большую частоту кадров, но приложение, построенное
на таймере, менее болезненно реагирует на потерю фокуса,
В таких случаях можно повышать приоритет процесса, этот прием мы рассмотрим
в главе 5.
Замечу, что при запуске приложения или изменении ею размеров требуется несколько
секунд, чтобы работа вошла в нормальный режим, поэтому первые цифры, выдаваемые
в качестве частоты воспроизведения, не являются особо надежными.
Теперь посмотрим, как реализовать фоновый режим в проектах, основанных только
на функциях API. Это иллюстрирует проект из подкаталога Ex70.
Пользовательская функция idle содержит код, связанный с изменениями кадра.
Для отслеживания состояния активности окна заведен флаг AppActive, а оконная
функция дополнилась обработчиком сообщения, связанного с активацией окна:
WM__ACTIVATEAPP:
If (wParara = WA^ACTIVE) or (wParam = WA__CLICKACTIVE)
then AppActive: = True
else AppActive: = False;
Кардинальные изменения коснулись цикла обработки сообщений, вместо которого появился вот такой вечный цикл:
While True do begln
// проверяем очередь на наличие сообщения
If PeekMessage (Message, 0, 0, 0, pm_NoRemove) then begln
// в очереди присутствует какое-то сообщение
If not GetMessage(Message, 0, 0, 0)
then Break // сообщение WM_QUIT, прервать вечный цикл
else begln // обрабатываем сообщение
TranslateMessage(Message);
DispatchMessage(Message);
end;
end
else // очередь сообщений пуста
If AppActive
then Idle // приложение активно, рисуем очередной кадр
else WaitMessage; // приложение не активно, ничего не делаем
end;
Надеюсь, все понятно по комментариям, приведу только небольшие пояснения.
Функция PeekMessage с такими параметрами, как в этом примере, не удаляет сообщение
из очереди, чтобы обработать его в дальнейшем традиционным способом.
Функция idle в этом примере вызывается при пустой очереди только в случае активности
приложения.
Код можно немного сократить, если не акцентироваться на том, активно ли приложение;
в данном же случае минимизированное приложение "засыпает". не внося
изменений в кадр.
Рассмотрим еше один прием, использующийся для построения анимационных приложений
и заключающийся в зацикливании программы. Для начала приведу самый простой способ
зацикливания программы (проект из подкаталога Ex71).
Сценарий не изменился, рисуется все то же подобие шестерни. Никаких таймеров
и прочих приемов, просто обработчик перерисовки окна заканчивается приращением
управляющей переменной и командой перерисовки региона (окна):
Angle: = Angle + 0. 1;
If Angle >= 360. 0 then Angle: = 0. 0;
InvalidateRect(Handle, nil, False);
Все просто: воспроизведя очередной кадр, подаем команду на воспроизведение
следующего.
В этом методе, как, впрочем, и в предыдущем, при уменьшении размеров окна частота
кадров увеличивается, но и вращение происходит быстрее, здесь так же отсутствует
контроль за поведением системы.
Приложение "замирает", будучи минимизированным
Если присмотреться внимательнее к поведению этого примера, то можно заметить
некоторые необычные вещи, например, при наведении курсора на системные кнопки
в заголовке окна подсказки не появляются. А при попытке активизации системного
меню окна появляется явная накладка в работе приложения, область меню требуется
перерисовать, двигая курсор в пределах его границ. Короче, зацикливание программы
приводит к тому. что ожидающие сообщения могут и не обрабатываться. Может, это
и не страшно, но ведь у нас нет гарантии, что мы обнаружили все странности работы
приложения.
Решение проблемы состоит в использовании функции processMessages объекта Application,
приостанавливающей работу приложения, чтобы система могла обрабатывать сообщения
из очереди
Посмотрим на проект из подкаталога Ex72. Перед перерисовкой окна обрабатываем
все сообщения очереди, вызвав функцию ProcessMessages, однако этого добавления
не достаточно, иначе приложение невозможно будет закрыть. В примере введен вспомогательный
флаг closed, принимающий исгинное значение при попытке пользователя или системы
закрыть приложение:
procedure TfrmGL. FormCloseQuery(3ender: TObject; var Car. Close: Boolean;
begin
Closed: = True end;
Теперь следующий кадр воспроизводится только в том случае, если не поступало сигнала о том, что приложение необходимо закрыть:
If not Closed then begin
Angle: = Angle + 0. 1;
If Angle >= 360. 0 then Angle: = 0, 0;
Application. ProcessMessages;
InvaIidateRect{Handle, nil, False);
end;
Этот вариант лишен недостатков предыдущего и реагирует на все поступающие сообщения,
но приобрел новую особенность: если, например, активировать системное меню окна
приложения, то вращение системы останавливается, пока меню не исчезнет.
Чтобы вы не забыли о том, что можно перемежать вывод командами OpenGL и обычными
средствами операционной системы, предлагаю в этом примере вывод частоты кадров
осуществлять не в заголовке окна, а на поверхности формы, заменив соответствующую
строку кода на такую:
Canvas. TextOut (0, 0, 'FPS - ' + FloatToStr (fpsRate));
При выводе на поверхность окна с помощью функций GDI не должно возникать проблем
ни с одной картой, а вот если попытаться текст выводить на метку, то проблемы,
скорее всего, возникнут со всеми картами: метка не будет видна.
Следующий пример, проект из подкаталога Ex73, является очередным моим переводом
на Delphi классической программы, изначально написанной на С профессиональными
программистами корпорации Silicon Graphics. Экран заполнен движущимися точками
так, что у наблюдателя может появиться ощущение полета в космосе среди звезд
(рис. 3. 39).
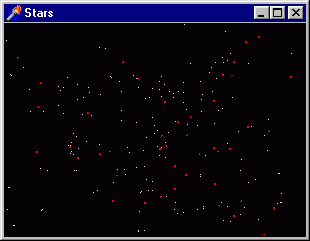
Рис. 3. 39. Проект Stars создает иллюзию полета в космосе
Предусмотрены два режима работы программы, управление которыми осуществляется
нажатием пробела и клавиши T'. После нажатия пробела некоторые звезды летят
по "неправильной" траектории, после нажатия второй управляющей, клавиши
происходит "ускорение" полета на некоторое время.
Последний прием, который мы разберем в этом разделе, основан на использовании
потоков. Проект из подкаталога Ex74 иллюстрирует этот прием на примере хорошо
нам знакомой по предыдущим упражнениям вращающейся шестерни. В программе введен
тип, ответственный за используемый поток:
type
TGLThread = class (TThread)
protected
procedure Execute;
override; // метод обязательно переопределяется
procedure Paint; // пользовательский метод потока
end;
Два метода потока описаны в традиционном стиле:
procedure TGLThread. Paint;
begln
With frmGL do begln
Angle: = Angle + 0. 1;
If Angle >=o 360. 0 then Angle: = 0, 0;
InvalidateRect(Handle, nil. False);
end;
end;
procedure TGLThread. Execute;
begln repeat
Synchronize (Paint); // синхронизация потоков
until Terminated;
end;
После создания окна поток инициализируется и запускается:
GLThread: = TGLThread, Create (False);
По окончании работы приложения выполняются стандартные действия:
GLThread. 3uspend; // приостановить поток
3LThread. Free; // удалить поток
В этом разделе мы рассмотрели несколько способов организации анимационных программ.
У каждого из этих методов есть свои достоинства и свои недостатки, и вы вольны
самостоятельно решать, какой из этих способов является для вас наиболее подходящим.
Если при уменьшении размеров окна частота воспроизведения увеличивается, это
является положительной стороной метода, но если в данном методе невозможно предугадать
поведение программы на разных машинах, то это можно отнести к его недостаткам.
Повторю, чго обработка ожидания является самым распространенным способом, и
при обычной нагрузке системы он должен показать максимальную частоту воспроизведения.
В оставшихся примерах лекций вы можете встретить самые разные из этих способов,
я не стану придерживаться какого-либо одного. Приведу еще один пример на анимацию,
проект из подкатачога Ex75, где используется обычный системный таймер. В примере
рисуется фонтан из двyx тысяч точек (рис. 3. 40).
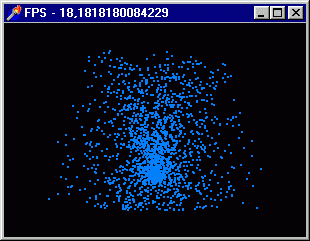
Рис. 3. 44. Проект Fontain, две тысячи капель
Как и в примере на звезды, в отдельных массивах хранится информация для каждого
объекта о текущем положении и направлении движения. на смену каждой "упавшей
точки" струя фонтана дополняется новой:
UpdatePOINT(i: Word); // процедура перемещения капли
begin
Points[i] [Qj: = points[i] [0] + motion[i] [0]; // изменение координат
points[i][l]. =points[i][l] +motion[i][l];
points[i][2]: =points[i][2] +motion[i][2];
If points[i][1] < -0. 75 then begin // капля фонтана упала на землю
points[i][0] = 0. 0; // новая капля вырывается из фонтана
points[i][1] = -0. 5;
pomts[i] [2] = 0. 0;
motion[i][0] = (Random-0. 5) / 20;
motion[i][l] = Random / 7 + 0. 01;
motion[i][2] = (Random-0. 5) / 20;
end
else motion[i][l}: = motion[i][1] - 0. 01; // условная сила тяготения
end;
Меняя значение силы тяготения, можно регулировать высоту фонтана. Последним примером главы станет проект из подкаталога Ex76, один из получающихся кадров работы программы приведен на рис 3. 41.

Рис. 3. 45. Теперь вы умеете рисовать даже такие "художественные произведения"
Если вы собираетесь распространять приложение, то позаботьтесь о том, чтобы ваше приложение на компьютерах сторонних пользователей не стало работать так быстро, что зритель ничего не сможет разглядеть на экране. Разберем, как это сделать. Предположим, управляющая переменная описана следующим образом
var
Angle: GLint = 0;
Вы пользуетесь не таймером, а скажем, зацикливаете программу Шаг увеличения переменной вы задаете так, что на вашем компьютере движение объектов происходит ровно и с удовлетворительной скоростью
Angle: = (Angle + 2) mod 360;
Может случиться, что на компьютере пользователя скорость воспроизведения окажется
в пять раз выше, и тогда объекты на сцене будут перемещаться в пять раз быстрее.
В таких случаях лучше опираться на системное время Например, введите переменную
для хранения текущего времени, а управляющую переменную задайте вещественной:
angle: GLfloat = 0; time: LongInt;
Если по сценарию полный оборот должен произойти за десять секунд, то код должен быть таким:
Angle: = Angle + 0. 1 * (GetTickCount - time)*3600/1000
If Angle >= 360. 0 then Angle: = 0. 0;
tme: = GetTickCount;
|
|