Теорема Котельникова

Владимир Александрович Котельников
(1908 - 2005)

Эта фундаментальная теорема показывает, что, если рассматриваемый сигнал ограничен некоторой частотой F сверху, то он может быть дискретизирован, то есть представлен дискретными измерениями с шагом во времени 2/F (полупериод граничной частоты), при этом дискретные измерения через 2/F несут без потерь всю информацию о сигнале.

В западной литературе совершенно бессовестно, в угоду принижения достижений СССР и России, а также в угоду прославления непричастных, но своих, ложно указывается, что данная теорема доказана, якобы, Шенноном и Найквистом. Когда же невозможно назвать ее ложным именем "теорема Найквиста - Шеннона", например, в русскоязычной литературе, то ее "скромно" называют "теоремой отсчетов".

Совершенно непонятна позиция некоторый российских писателей и лекторов, которые называют ее теоремой Шеннона - Котельникова. Из компромиса? - Разве может быть компромис между истиной и ложью?

На самом деле в 1933 году, когда эта теорема была опубликована В.А. Котельниковым в его работе "О пропускной способности эфира и проволоки в электросвязи", Шеннону было 17 лет. В тот год Клод Шеннон (1916 г.р.) только окончил среднюю школу и поступил работать курьером-разносчиком в один из офисов в своем городе, а о теории информации еще слухом не слыхивал.

В трудах Найквиста до сих пор не найдено доказательство этой теоремы, но лишь рассуждения вокруг этой темы. Однако рассуждения на тему и доказательство теоремы - разные вещи.

Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром сформулировано, доказано и опубликовано в 1933 году В. А. Котельниковым: «Любая непрерывная функция s(t), спектр которой ограничен частотой F_max полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал 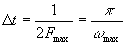» Кроме того, теорема Котельникова дает и способ точного восстановления сигнала 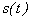по его отсчетам.

Доказательство

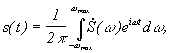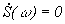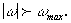причем при (1)

Разложим функцию 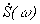в частотной области на конечном интервале 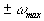(с периодом 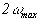) в комплексный ряд Фурье :

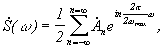где (2)

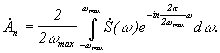(3)

Сравнивая интегралы в (3) и (1), видно, что они равны при 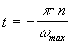, т. е. 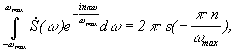тогда

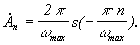(4)

Подставляем (4) в (2), а затем в (1)

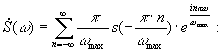
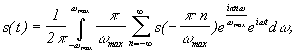
т. к. суммирование по от -¥ до +¥, то можно заменить знак у .

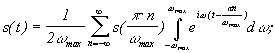
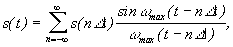
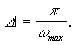(5)

Максимальные значения членов ряда будут при 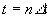и равны 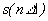, при этом все остальные члены ряда равны нулю, т. е. при 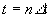функция s(t) точно передается рядом. Во все другие моменты времени необходимо суммировать бесконечное число отсчетов, чтобы передать s(t) точно.

к оглавлению

Знаете ли Вы, что в 1965 году два американца Пензиас (эмигрант из Германии) и Вильсон заявили, что они открыли излучение космоса. Через несколько лет им дали Нобелевскую премию, как-будто никто не знал работ Э. Регенера, измерившего температуру космического пространства с помощью запуска болометра в стратосферу в 1933 г.? Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира