ПОВЫШЕНИЕ СКОРОСТИ ПЕРЕДАЧИ СИГНАЛОВ ПО КАБЕЛЮ

Гораздо труднее увидеть проблему, чем найти ее решение. Для первого требуется воображение, для второго - только умение.

Джон Бернал. Английский физик, ХХ в.

Содержание: Введение. 15.1. Фильтр восстановления формы сигналов. Общая методика синтеза фильтров. Точность воспроизводства формы импульсов. Усиление шумов. 15.2. Фильтр восстановления кодовых сигналов. Оператор фильтра. Предельная частота передачи данных. Кодовые сигналы. 15.3. Принципы реализации фильтров частичной деконволюции. Литература.

Введение

Принципы частотной коррекции сигналов при их искажениях в линиях связи известны /23/. Отметим сразу, что говорить о метрологически точном восстановлении сигналов с определенной погрешностью, задаваемой метрикой выходного и входного сигналов, имеет смысл только в том случае, если эффективная ширина спектра сигналов много меньше эффективной ширины спектра импульсного отклика кабеля и затухает достаточно быстро. Если эти условия выполняются, то полная частотная коррекция передачи сигналов может быть выполнена инверсией импульсного отклика кабеля (без учета временной задержки сигналов). Такая инверсия, в принципе, возможна, но практического интереса не представляет. Это определяется тем, что спектральная плотность импульсного отклика жил кабелей меньше 1 по всему частотному диапазону с затуханием, близким к монотонному, также по всему частотному диапазону, начиная с частот 1-10 кГц. Фильтры деконволюции таких импульсных откликов имеют значительные (до нескольких тысяч) коэффициенты усиления дисперсии шумов, а потому рассматривать этот вариант не имеет смысла. Соответственно, для широкополосных сигналов, передаваемых по кабелю, возможна только частичная деконволюция импульсного отклика жил, т.е. применение фильтров сжатия импульсных откликов жил до определенной формы. Оптимальной с позиции минимального значения коэффициента усиления дисперсии шумов в этом случае считается симметричная гауссовская форма выходных импульсов фильтров частичной деконволюции (ЧД) импульсных откликов.

Методику расчета фильтров ЧД будем рассматривать в общей форме, возможности технической реализации в реальном масштабе времени в аналоговой форме (трансверсальные фильтры на линиях задержки) и в чисто цифровой форме с использованием амплитудно-цифровых преобразователей (АЦП) при дискретизации сигналов на выходе кабеля и микропроцессоров обработки цифровых данных в реальном масштабе времени.

15.1. Фильтр восстановления формы сигналов

Коррекция формы выходных сигналов обычно применяется только для кабелей небольшой длины при прямой передаче сигналов геофизических детекторов на измерительные приборы. С учетом этого, все нижеследующие расчеты выполняются в качестве примера для кабеля КГ 1х0.75-55-150 длиной 2 км.

Общая методика синтеза фильтров ЧД (которая в следующем разделе будет использоваться и для расчетов фильтров ЧД кодовых импульсных сигналов) включает следующие операции:

1. Задание длины кабеля, определение его импульсного отклика и сдвиг отклика (по началу значимых значений фронта) в начало координат. Сдвинутую функцию будем считать амплитудным откликом h(t) кабеля (без учета задержки сигнала) и выполняем преобразование Фурье h(t) Ю H(w).

2. Задание формы выходного импульса z(t) фильтра ЧД в виде гауссовской функции (или любой другой с ограниченным и быстро затухающим спектром) и определение его спектра z(t) Ы Z(w). Временное расположение импульса z(t) должно быть таким, чтобы площадь импульса практически полностью располагалась за пределами фронта импульсного отклика кабеля h(t). Максимум z(t) должен располагаться за максимумом отклика кабеля. В принципе, он может задаваться на максимуме и до максимума импульсного отклика, но это ухудшает параметры оператора ЧД. Площадь z(t) при метрологической коррекции сигналов должна быть равна площади импульсного отклика. При восстановлении кодовых сигналов этот параметр не нормируется.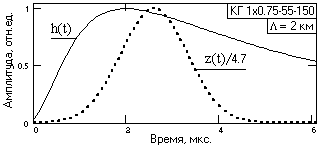

Рис. 15.1.1. Форма импульсов.

На рис. 15.1.1 приведены примеры формы сигналов, нормированные по амплитуде к 1 для наглядности сравнения. Ширина гауссовского импульса (значение стандарта – среднеквадратического отклонения от центра импульса) подбирается по допустимому коэффициенту усиления дисперсии шумов (после расчета оператора ЧД). Для приведенных далее расчетов площади импульсов установлены равными, ширина импульса z(t) установлена такой, чтобы коэффициент усиления дисперсии шумов был не более 4 (амплитудное усиление шумов не более 2), при этом амплитудное усиление сигналов порядка 4.7, что позволяет повысить отношение сигнал/шум не менее чем в 2 раза.

3. Вычисление спектральной плотности передаточной функции фильтра ЧД, которое выполняется по формуле:

Hd(w) = Z(w)/H(w). (15.1.1)

При равных площадях импульсного отклика кабеля и функции z(t) значения спектров Z(w) и H(w) при w=0 равны и, соответственно, их отношение равно 1, т.е. коэффициент усиления фильтром ЧД постоянной составляющей равен 1. Для фильтров ЧД кодовых импульсов этот параметр не регламентируется. Более того, при коэффициенте усиления постоянной составляющей менее 1 фильтр ЧД в определенной мере стабилизирует нулевую линию сигналов.

Функция Hd(w) имеет смысл в области значимых значений H(w) и за пределами этой области обнуляется, что исключит усиление высокочастотных шумов кабеля. Усечение, начиная с определенной частоты w_c, целесообразно выполнять весовой гауссовской функцией:

Hd(w) = Hd(w)Ч exp(-a(w_c+w)²), w і w_c. (15.1.2)

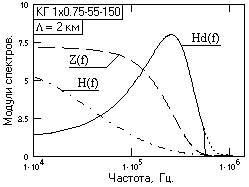
Пример формы спектральной плотности фильтра ЧД приведен на рис. 15.1.2 в сопоставлении со спектрами исходных импульсов (масштаб спектров импульсов для наглядности увеличен). Пунктиром на рисунке показана усеченная часть функции Hd(w).

Коэффициент усиления фильтром дисперсии входных статистических шумов при равномерном распределении шумов в диапазоне от 0 до W:

K_e = (1/W) |Hd(w)|² dw. (15.1.3)

По рисунку 15.1.2 нетрудно сделать заключение, что коэффициент усиления фильтром ЧД дисперсии статистических шумов больше 1 и существенно зависит от эффективной ширины спектра импульса z(t). Чем меньше значение DW импульса z(t) (больше эффективная ширина DT импульса), тем меньше коэффициент усиления дисперсии шумов.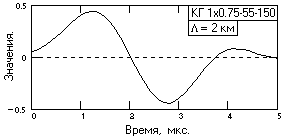

Рис. 15.1.3. Оператор ЧД.

4. Обратным преобразованием Фурье функции Hd(w) вычисляется оператор фильтра ЧД: Hd(w) Ю hd(t). Пример оператора, нормированного на интервал дискретизации данных Dt = 0.1 мкс для цифровой обработки сигналов, приведен на рис. 15.1.3 и получен по исходной функции Hd(w) рис. 15.1.2. Коэффициент усиления дисперсии шумов данного оператора равен 3,4. При заданном на рис. 15.1.1 коэффициенте усиления амплитуды импульса z(t) порядка 4.7 это дает улучшение отношения сигнал/шум в 4.7/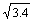» 2.5 раза при равномерном распределении шумов в интервале от 0 до W = 1/(2Dt).

При подаче на вход кабеля импульса Кронекера d_o на выходе фильтра будем иметь:

s(t)=d_o*h(t)_*hd(t) Ы 1Ч H(w)Ч Hd(w)=Z(w) Ы z(t),

т.е. выходной единичный импульс вместо асимметричной формы импульсного отклика кабеля будет иметь симметричную форму гауссовского импульса. Аналогичным является и результат непосредственной свертки импульсного отклика с оператором фильтра ЧД, что может использоваться для контроля расчетов операторов фильтров ЧД.

Точность воспроизводства формы заданной функции выходного импульса определяется размером оператора ЧД, который имеет существенное значение при его технической реализации в виде трансверсальных фильтров на линиях задержки. Основная часть энергии оператора (более 99%) сосредоточена в пределах интервала, примерно равного (2-3) значениям фронта импульсного отклика, т.е. начальная часть импульсного отклика содержит практически всю информацию о форме сигналов на входе кабеля. Однако, вследствие достаточно длинного спада отклика с постепенным уменьшением скорости спада, ограничение размера оператора ЧД короткой значимой частью приводит к появлению на его выходе послеимпульсных “выбросов” с амплитудным значением до 2% от максимальной амплитуды выходного сигнала (чем меньше размер оператора ЧД, тем больше амплитуда выбросов) и c длительностью, равной соответствующей длительности значимой части импульсного отклика (с постепенным затуханием). Положение послеимпульсного "хвоста" (включая первый отрицательный выброс) относительно нулевой линии может смещаться изменением концевого значения оператора ЧД.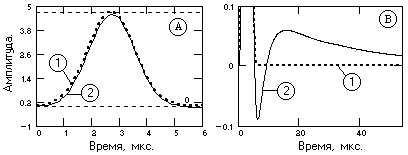

Рис. 15.1.4. Свертка импульсного отклика с оператором ЧД.

На рис. 15.1.4 приведены результаты свертки (кривая 2) импульсного отклика кабеля с оператором ЧД размером 4.2 мкс при временной длине значимой части импульсного отклика кабеля (более 0.01 максимального значения) порядка 70 мкс. Кривая 1 – заданная функция z(t). Как видно на графике А, форма заданного импульса сжатия реализуется достаточно точно. Среднее квадратическое расхождение с заданной формой z(t) – 0.024, отрицательный выброс не более 2% от амплитуды при центрировании "хвоста" относительно нулевой линии (график B).

На рис. 15.1.5 приведено сопоставление формы импульсов на входе кабеля, заданных на интервалах 2DT_k, на выходе кабеля (на входе фильтра ЧД) и на выходе фильтра ЧД. Для фильтрации использован оператор ЧД, приведенный на рис. 15.1.3, размером 4.2 мкс. Амплитудные значения сигналов на входе кабеля умножены на площадь импульсного отклика (учет безвозвратных электромагнитных потерь), и сдвинуты во времени для сопоставления формы к сигналам на выходе фильтра ЧД.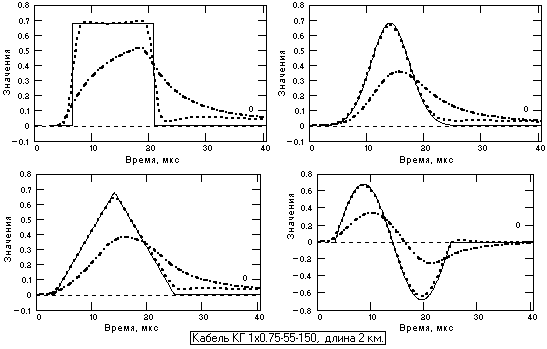

Рис. 15.1.5. Формы сигналов на входе (сплошные линии), на выходе кабеля (штрих-пунктир)

и на выходе фильтра ЧД (пунктир). Входные сигналы смещены во времени.

Как видно на графиках, форма сигналов со значением DW, соизмеримом и меньшим значения DW_k, восстанавливается достаточно хорошо (со среднеквадратической погрешностью в пределах сигнала не более 1% относительно амплитудного значения), но для однополярных сигналов значение накопленного послеимпульсного “хвоста” возрастает до 5% от амплитуды сигнала. Если “хвост” послеимпульса должен быть ограничен по амплитуде определенной величиной, то это выполняется увеличением размера оператора фильтра ЧД. При длине оператора, равной длине импульсного отклика кабеля, амплитуда послеимпульса уменьшается более чем на порядок. Для прямоугольных импульсов при DW > DW_к погрешность, естественно, возрастает за счет сглаживания фронтов, но остается в пределах не более (2-3)% по амплитудным значениям.

Усиление шумов. На рис. 15.1.6 приведены графики модельного статистического шума на входе (сплошная линия) и на выходе (пунктир) фильтра ЧД с параметрами, описанными выше. По результатам моделирования коэффициент усиления дисперсии шумов полностью соответствует расчетному значению (расчетное – 3.4, модельное на односекундном интервале – 3.38). Фильтр ЧД сглаживает шумы в соответствии со своей частотной характеристикой, и форма выходных шумов становится похожей на форму произвольных сигналов.

Рис. 15.1.6. Форма шумовых сигналов на входе и на выходе фильтра ЧД (пунктир).

Усиление шумов может существенно усложнить метрологическое восстановление произвольных сигналов. На рис. 15.1.7 приведен пример фильтрации зашумленного сигнала при среднеквадратическом уровне шума порядка 10% от амплитудных значений входного сигнала. Заметим, что хотя частотный диапазон спектра статистических шумов на выходе кабеля значительно превышает частотный диапазон сигналов, любые линейные методы фильтрации сигналов (подавления шумов) в данном случае не имеют смысла. Оператор ЧД, как это следует из (15.1.2) и можно видеть на рис. 15.1.2, самостоятельно подавляет все высокочастотные шумы.

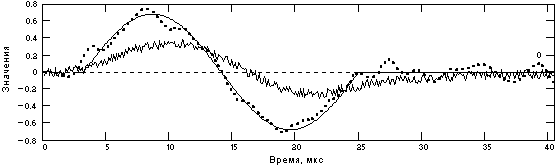
Рис. 15.1.7. Форма сигнала с шумом на входе и на выходе фильтра ЧД (пунктир).

При использовании цифровых методов обработки данных плавная форма выходных информационных сигналов с априорно известными параметрами их динамики позволяет использовать до подачи сигналов на фильтр ЧД нелинейные методы фильтрации, и в частности – адаптивные фильтры, не изменяющие динамики информационных сигналов при подавлении шумов, в том числе перекрывающихся по частотному диапазону с частотным диапазоном сигналов.

15.2. Фильтр восстановления кодовых сигналов

Методика синтеза фильтров ЧД на кодовые сигналы практически полностью повторяет методику расчетов при восстановлении формы сигналов. Все нижеследующие расчеты выполняются в качестве примера для кабеля КГ 3х0.75-60-150 длиной 5 км для цифрового фильтра ЧД при интервале дискретизации данных 0.1 мкс. Импульсные параметры кабеля: DT_k » 26 мкс, DW_k » 34 кГц.

Оператор фильтра. При приеме кодовых сигналов главное значение имеет простота и надежность выделения кода, которая определяется надежностью выделения единичных битовых импульсов. Для кода Манчестер-II она определяется интервалом минимум-максимум в непрерывной последовательности единиц (нулей). Для кодов NRZ и RZ имеет значение и сдвиг нулевой линии. Форма выходных импульсов особого значения не имеет, если не нарушается пространственное распределение импульсов. Естественно, что на предельной частоте передачи сигналов при достаточно высокой степени их амплитудного затухания существенное значение имеет увеличение (или, по крайней мере, сохранение на прежнем уровне) выходного отношения сигнал/шум фильтром ЧД.

При использовании фильтра ЧД можно считать, что предельная пропускная способность кабеля должна быть оценена с ограничением параметров оператора ЧД по определенному допустимому уровню коэффициента усиления дисперсии шумов. Примем этот уровень для дальнейших расчетов равным 1, т.е. оператор ЧД не должен усиливать среднеквадратичный уровень шумов. Это обеспечивается заданием соответствующей длительности импульса z(t) на половине высоты гауссовского пика (в данном случае порядка 7-8 мкс).

Пример оператора, и результат его проверки сверткой с импульсным откликом жилы кабеля приведен на рис. 15.2.1. Длительность оператора 20 мкс, коэффициент усиления дисперсии шумов ~0.65, коэффициент усиления амплитуды импульсного отклика жилы ~3.8.

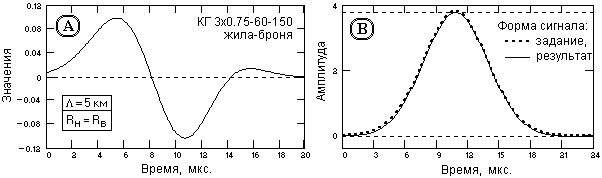
Рис. 15.2.1. Оператор фильтра ЧД кодов.

Предельная частота передачи данных. В качестве входных импульсов кабеля имеет смысл рассмотреть только прямоугольные импульсы, фронты которых на выходе фильтра ЧД будут соответственно сглажены до величины порядка ширины импульса z(t). Эффект применения фильтра ЧД можно видеть на рис. 15.2.2 на примерах кодовой последовательности биполярных импульсов с единичной амплитудой на тактовых интервалах Т = 2Ч DT_k, Т = DT_k и Т = 0.5Ч DT_k мкс (тактовые частоты 19, 38 и 76 кГц). Пунктиром на рисунке показаны входные импульсы, приведенные к выходу кабеля с учетом безвозвратных потерь и задержки в кабеле.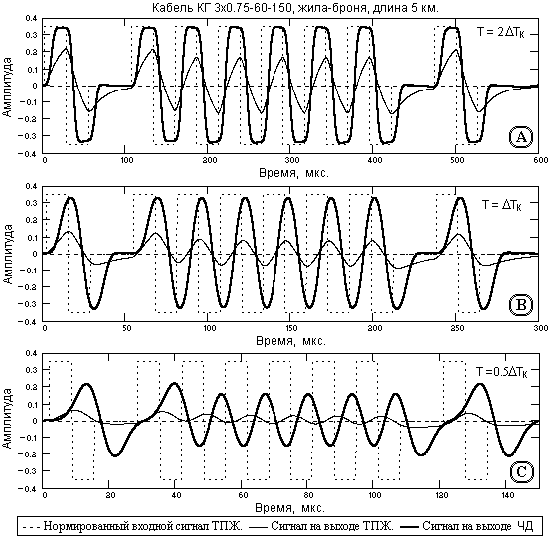

Рис. 15.2.2. Биполярные импульсы на входе и на выходе фильтра ЧД

Как следует из этого рисунка, применение фильтра ЧД позволяет уменьшить предельный тактовый интервал следования битовых импульсов при идентификации кода минимум в 2 раза, т.е. в 2 раза увеличить скорость передачи информации по кабелю.

Заметим, что при коэффициенте усиления дисперсии шумов данного оператора ЧД не более 1 отношение сигнал/шум на выходе фильтра ЧД при статистических шумах на входе улучшается практически в 2 раза, т.к. оператор ЧД в этом случае выполняет и роль низкочастотного сглаживающего фильтра. О последнем наглядно свидетельствует рис. 15.2.3(A).

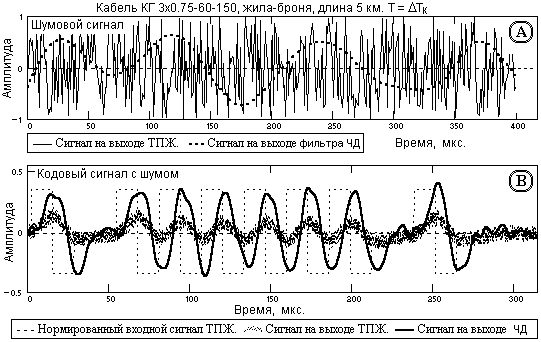
Рис. 15.2.3. Преобразование шумов и сигналов с шумом фильтром ЧД.

Пример фильтрации сигналов с наложенным статистическим шумом, средние квадратические флюктуации которого составляют порядка 30% от амплитуды информационных импульсов, приведен на рис. 15.2.3(B) и показывает уверенное сохранение информационной структуры сигнала.

Кодовые сигналы. На рис. 15.2.4(A) показана деконволюция кодовых сигналов с тактовой частотой 38 кГц, приведенных ранее на рис. 14.3.1 без деконволюции на предельной тактовой частоте 19 кГц. Как следует из рисунка, деконволюция позволяет практически полностью восстановить амплитудные значения сигналов (за вычетом безвозвратных потерь) на удвоенной тактовой частоте, т.е. импульсная пропускная способность кабеля повышается минимум в 2 раза для всех видов кодирования. Что касается предельной импульсной пропускной способности кабеля, то она повышается практически в 4 раза по сравнению с приемом сигналов без деконволюции, о чем достаточно наглядно свидетельствует пример формы тех же кодовых сигналов на тактовой частоте 76 кГц, приведенный на рис. 15.2.4(B), и сравнение этого рисунка с рисунком 14.3.1(B). Преимущество кода Манчестер-II перед кодами NRZ и RZ при использовании частичной деконволюции очевидно как на рис. 15.2.4(A), так и на рис. 15.2.4(B). С определенным запасом "прочности" можно считать, что при передаче информации биполярными кодами скорость передачи данных с использованием частичной деконволюции импульсного отклика кабеля может быть увеличена в 3 раза.

Краткие выводы по возможностям повышения импульсной пропускной способности каротажных кабелей:

1. Качество приема и надежность идентификации кодовой информации на выходе кабеля могут быть существенно повышены при частичной деконволюции импульсного отклика кабеля до симметричной (гауссовской) формы.

2. Основная (значимая) часть энергии оператора частичной деконволюции импульсного отклика кабеля сосредоточена в пределах 2-3 значений фронта отклика.

3. Для финитных сигналов, задаваемых на интервале не менее 2DT_к и имеющих эффективную ширину спектра не более DW_к, частичная деконволюция импульсного отклика жил кабеля обеспечивает восстановление формы сигналов с погрешностью по основным метрологическим параметрам (амплитуда, площадь, временная привязка) не более (1-2)%.

4. Скорость передачи кодовых данных при использовании частичной деконволюции импульсного отклика может быть увеличена минимум в 2 раза при любых методах кодирования и равна 1/DT_к. При передаче информации биполярными импульсами предельная скорость передачи данных может быть увеличена минимум в 3 раза.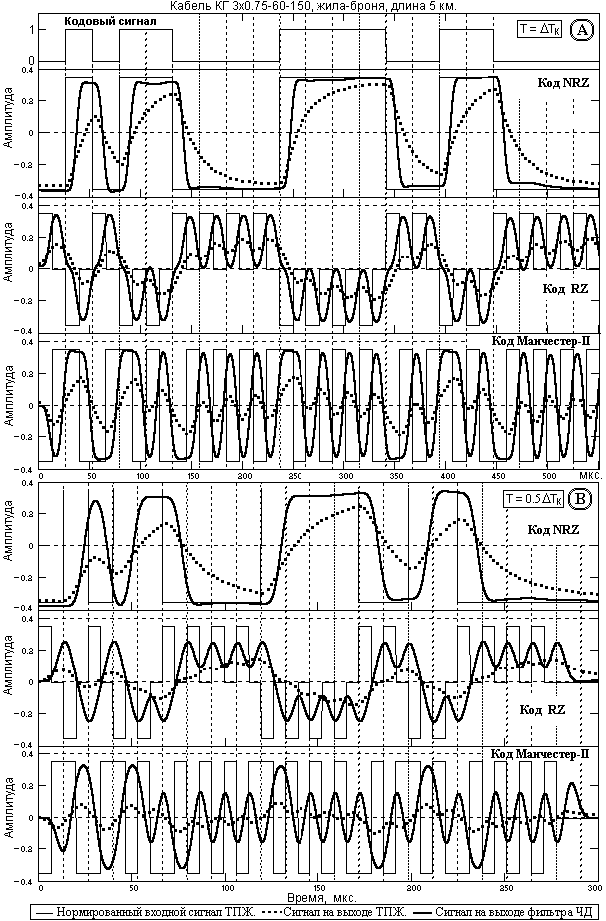

Рис. 15.2.4. Деконволюция кодовых выходных сигналов, тактовые частоты 38 и 76 кГц.

15.3. Принципы реализации фильтров частичной деконволюции

Основное условие технической реализации фильтров ЧД – работа в реальном масштабе времени. Дополнительное и желательное условие – полная автономность от аппаратурного блока каротажных станций, позволяющая включать фильтры ЧД на выход кабеля в состав любой станции, если в том появится необходимость.

Достаточно простая форма передаточной функции фильтра ЧД позволяет выполнить его реализацию непосредственно в виде аналогового нерекурсивного или рекурсивного фильтра. Следует отметить, что такие фильтры будут являться индивидуальными для кабелей различных типов и различной длины (в определенных пределах возможной подстройки) и могут отличаться по исполнению: нерекурсивные - для фильтров с короткой функцией отклика, и рекурсивные для кабелей длиной 3 и более км.

С учетом современных темпов развития электроники перспективным и универсальным направлением следует считать цифровые фильтры, т.е. микропроцессорное исполнение фильтров ЧД или программное выполнение фильтров в составе каротажных измерительно-вычислительных комплексов непосредственно на их входе. Заметим, что детерминированность кодовых сигналов позволяет выполнять микропроцессорные ЧД с автоматической адаптацией под конкретный кабель, стоящий на каротажной станции.

Своеобразной комбинацией дискретного синтеза с аналоговым процессом фильтрации являются трансверсальные фильтры на линиях задержки. Исходные условия для их реализации аналогичны цифровым фильтрам.

Возможность цифрового исполнения фильтров ЧД можно оценить по таблице 15.3.1. При определении частоты Найквиста цифрового фильтра ЧД по предельной частоте f_пр передаточной функции кабеля (по уровню порядка 1% от коэффициента передачи на низких частотах) значение шага дискретизации данных на выходе кабеля находится в диапазоне 0.2-6 мкс в зависимости от длины кабеля. Этот диапазон достаточно хорошо согласуется с шагом дискретизации данных по предельной тактовой частоте передачи информации биполярными импульсами (частота Найквиста за третьей гармоникой тактовой частоты, что обеспечивает регистрацию более 98% энергии сигналов).

Таблица 15.3.1. Параметры передачи данных (кабель КГ 3х0.75-60-150, жила-броня).

Длина кабеля	км	1	2	3	4	5	6	7
Предельная частота f_пр [по уровню 0.01К_max]	кГц	2460	718	358	220	151	111	85
Шаг дискретизации на предельной частоте (1/2f_пр)	мкс	0.2	0.7	1.4	2.3	3.3	4.5	5.9
Эффективная ширина импульсного отклика DT_к	мкс	3.3	8.6	14.1	19.9	26.1	33.1	40.9
Тактовая частота передачи данных f_Т=1/DT_к	кГц	306	117	71	50.3	38.3	30.3	24.4
Шаг дискретизации по тактовой частоте (1/4f_Т)	мкс	0.4	1.0	2.2	2.5	3.3	4.1	5.1
Размер оператора ЧД (>98% энергии оператора)	мкс	2.6	5.1	9	13.5	19	25	32
Оптимальный шаг дискретизации данных Dt	мкс	0.12	0.24	0.4	0.65	1	1.2	1.5

В принципе, эти значения шага дискретизации данных вполне достаточны для обработки сигналов, четкой автосинхронизации тактовой частоты приема данных и их кодовой идентификации, а при необходимости и полного восстановления аналоговой формы сигналов. Для исключения трансформации высокочастотных шумов в рабочий диапазон сигнала, фильтру ЧД должен предшествовать аналоговый низкочастотный фильтр.

Коэффициент усиления дисперсии статистических шумов оператором цифрового фильтра, равный сумме квадратов значений его коэффициентов, зависит от интервала дискретизации. В данном случае, при постоянной заданной форме импульса z(t) сжатия импульсного отклика кабеля и увеличении значений Dt шага дискретизации (относительно Dt Ю 0 для аналоговой формы фильтра) количество коэффициентов оператора ЧД в пределах его импульсного отклика уменьшается, а их значения возрастают, что вызывает соответствующее возрастание коэффициента усиления дисперсии статистических помех. Для сохранения значения коэффициента усиления дисперсии помех на уровне, не большем 1, приходится увеличивать задаваемую ширину импульса z(t), при этом уменьшается амплитуда импульса z(t) и качество деконволюции сигнала. Это можно наглядно видеть на рис. 15.3.2 и 15.3.3.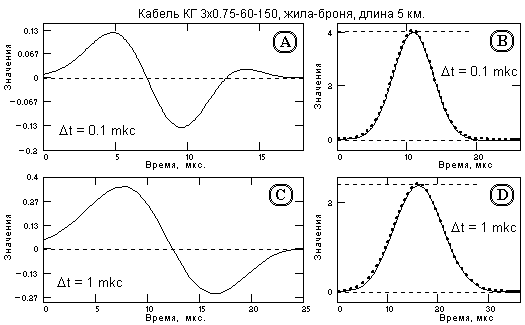

Рис. 15.3.2. Операторы ЧД (А, С) и форма сигналов сжатия импульсного

отклика кабеля (B,D) при разном шаге дискретизации данных.

На рис. 15.3.2 (А, С) приведены два оператора ЧД, вычисленные с разным шагом дискретизации данных (0.1 и 1 мкс). Ширина гауссовских импульсов z(t) (приведены пунктиром на рис. 15.3.2 (B,D)), была установлена такой, чтобы коэффициенты усиления дисперсии помех операторов ЧД были примерно равными в пределах 0.95-1.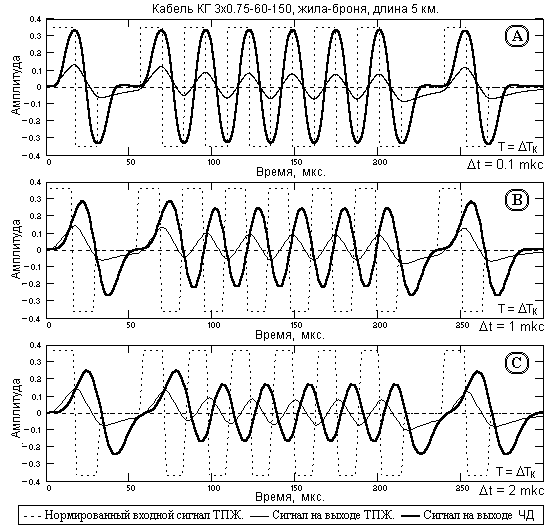

Рис. 15.3.3. Деконволюция выходных сигналов при разных интервалах дискретизации.

Как видно на рисунке, интервалу дискретизации 1 мкс соответствует в 1.5 раза большая ширина импульса z(t), чем интервалу дискретизации 0.1 мкс, и, соответственно, меньшая амплитуда импульса. Качество работы операторов по реализации заданной формы импульса z(t) при свертке с импульсным откликом кабеля практически одинаково (сплошные линии на рис. 15.3.2(B,D)), но при деконволюции импульсного кода оператор с большим шагом дискретизации данных соответственно имеет меньшую временную разрешающую способность и занижает амплитуды восстановленных импульсов, что можно видеть на рис. 15.3.3 (А, В). Дополнительно на рис. 15.3.3(С) приведен пример деконволюции сигнала с шагом дискретизации данных 2 мкс (оператор ЧД – 32 мкс, 16 точек, коэффициент усиления дисперсии шумов 0.98).

При сопоставлении графиков на рис. 15.3.3 можно сделать вывод, что оптимальный шаг дискретизации данных для цифрового фильтра ЧД соответствует 20-30 коэффициентам фильтра в пределах длительности значимой части оператора ЧД. Этот вывод подтверждают аналогичные вычисления и для кабелей других размеров. Соответственно, диапазон оптимальных значений шага дискретизации данных на входе фильтра ЧД, показанных в последней строке таблицы 15.3.1, установлен по длине операторов ЧД и составляет от 0.12 до 1.5 мкс. В принципе, такой тактовый диапазон при 20-30 операциях умножения и сложения вполне доступен для современных микропроцессорных систем, особенно для кабелей большой длины, для которых фильтр ЧД и необходим в максимальной степени.

В трансверсальных фильтрах сигнал с кабеля подается на последовательную цепочку линий задержки, в каждой из которых осуществляется задержка сигнала на интервал дискретизации данных. К выходам линий задержки подсоединена матрица резисторов, значения которых обратно пропорциональны значениям коэффициентов оператора ЧД. Токи через резисторы, пропорциональные положительным и отрицательным значениям коэффициентов оператора, суммируются раздельно (на входах двух операционных усилителей), после чего из "положительного" тока вычитается "отрицательный" и результат подается на вход аппаратуры станции, как выходной сигнал фильтра ЧД. Трансверсальный фильтр идеально приспособлен для исполнения в качестве автономного промежуточного блока между кабелем и станцией. При переменных сопротивлениях резисторной матрицы фильтр легко подстраивается под любой тип и любую жилу кабеля, а изменение длины кабеля с изменением интервала дискретизации данных выполняется заменой линии задержки. Некоторые технические трудности могут возникать только в наборе линий задержки для длинных кабелей (большое время задержки) с проявлением дополнительного затухания сигнала в самой ЛЗ, но последнее компенсируется соответствующим изменением коэффициентов резисторной матрицы.

Возможно и комбинированное цифро-аналоговое исполнение фильтра ЧД, в котором роль ЛЗ исполняет сдвиговый цифровой регистр с АЦП на входе (тактовая частота сдвига определяет шаг дискретизации входных данных), каждая цифровая ячейка которого имеет обратный резисторный ЦАП. Дальнейшая обработка токов ЦАП и формирование выходного сигнала аналогично трансверсальному фильтру. Для кодовых сигналов объем цифровых ячеек регистра может быть в пределах 5-7 двоичных разрядов. В таком исполнении фильтр ЧД становится автономным универсальным блоком с простой и гибкой настройкой под любой тип кабеля любой длины с изменением интервала дискретизации данных частотой тактового сдвига цифрового регистра.

Таким образом, каких-либо особых препятствий в технической реализации фильтров ЧД не имеется.

литература

23. Стрижевский Н.З. Коаксиальные видеолинии. – М.: Радио и связь, 1988. – 200 с.

к оглавлению

Знаете ли Вы, что, как ни тужатся релятивисты, CMB (космическое микроволновое излучение) - прямое доказательство существования эфира, системы абсолютного отсчета в космосе, и, следовательно, опровержение Пуанкаре-эйнштейновского релятивизма, утверждающего, что все ИСО равноправны, а эфира нет. Это фоновое излучение пространства имеет свою абсолютную систему отсчета, а значит никакого релятивизма быть не может. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира