МНОГОМЕРНЫЕ СИГНАЛЫ И СИСТЕМЫ
Когда ты смотришь в бездну, бездна смотрит в тебя.
Фридрих Ницше. Немецкий философ-моралист, ХIХ в.
Содержание:
Введение. 18.1. Двумерные и многомерные сигналы. 18.2. Двумерные системы. Импульсный отклик систем. Двумерная свертка. 18.3. Частотные характеристики сигналов и систем. Частотный отклик системы. Импульсный отклик системы. Свойства двумерного преобразования Фурье. 18.4. Дискретизация двумерных сигналов. Прямоугольный растр дискретизации. Дискретные преобразования Фурье. Интерполяционный ряд восстановления двумерного сигнала. Произвольный растр дискретизации. Интерполяция дискретных сигналов. Прямоугольный и гексагональный растры дискретизации. 18.5. Частотный анализ многомерных сигналов. Периодические последовательности. Конечные последовательности. Многомерные последовательности. Литература.Введение.
Обработка многомерных сигналов, используя в частных случаях методы обработки одномерных сигналов, имеет и существенные особенности. Это объясняется тремя факторами. Во-первых, математические методы описания многомерных систем далеки от совершенства и завершенности. Во-вторых, при решении многомерных задач используется значительно больший объем данных. И в третьих, многомерные системы обладают большим числом степеней свободы и, соответственно, значительно большей гибкостью. Так, например, при дискретизации информации в одномерном случае устанавливается только частота отсчетов, а в многомерном не только частота, но и форма растра дискретизации. С другой стороны, многомерные полиномы разлагаются на множители только в частном случае, а, следовательно, многие одномерные методы не обобщаются на случай многомерных задач.
Ниже будут рассматриваться сигналы и системы с размерностью два и более, при этом основное внимание будет уделяться двумерным задачам, имеющим широкое распространение в геофизической практике. Повышение размерности выше двух не приводит к качественным отличиям от двумерных случаев, кроме повышения сложности вычислений.
Многомерная информация в своем абсолютном большинстве, это дискретная информация в цифровой форме – многомерные массивы данных. Многомерные непрерывные функции используются только в чисто теоретических исследованиях. Даже двумерных данных, непрерывных (аналоговых) по обоим аргументам практически не существует. С учетом этого ниже рассматриваются, в основном, многомерные сигналы в дискретной форме.
18.1. Двумерные и многомерные сигналы [9].
Понятие многомерного сигнала.
Многомерные сигналы представляют собой функции P независимых переменных при P>1. В общем случае, сигнал может быть непрерывным, дискретным или смешанным. Понятия непрерывности и дискретности аналогичны одномерным сигналам. Что касается смешанного сигнала, то это многомерный сигнал, который описывается функцией некоторого количества непрерывных и некоторого количества дискретных переменных. Пример смешанного двумерного сигнала: ансамбль непрерывных сигналов, изменяющихся во времени (t - вторая переменная), снимаемых с набора сейсмических приемников сейсмотрассы (номера датчиков - первая переменная).В общем случае, двумерный непрерывный сигнал представляет собой функцию, значения которой зависят от двух независимых переменных (аргументов, координат):
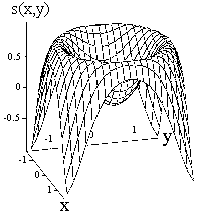
s(x,y) = sin(x2+y2), -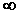 < x,y <
< x,y <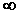 (18.1.1)
(18.1.1)
График функции (в пределах одного периода) приведен на рис. 18.1.1.
Двумерный дискретный сигнал (цифровой массив) - это функция, определенная на совокупности пар числовых значений координат с определенным шагом дискретизации
Dx и Dy. В общем случае, при различной физической размерности аргументов x и y, значения Dx и Dy не равны друг другу:sn,m = s(nDx,mDy), -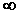 < n,m <
< n,m <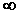 . (18.1.1')
. (18.1.1')
Элемент последовательности s
n,m представляет собой отсчет двумерной функции s в координатной точке (x=nDx,y=mDy), где значения x и y – независимые переменные (аргументы) функции. Для числовых массивов значения шага дискретизации по аргументам также могут приниматься равными 1 (независимо от размерности) и использоваться аргументация s(n,m) є sn,m. Результаты геофизических съемок какого-либо одного геофизического параметра по поверхности земли относятся к двумерным функциям: дискретным - если это отсчеты в отдельных точках по определенной координатной сети (x,y), или смешанным - если это непрерывная регистрация данных по профилям (например - мощности экспозиционной дозы гамма излучения горных пород при аэросъемке). Но в настоящее время геофизические съемки относятся даже не к двумерным, а к многомерным функциям, так как регистрируется, как правило, сразу несколько физических параметров геологических сред. Так, например, при спектрометрической съемке естественной радиоактивности горных пород регистрируется содержание в горных породах урана, тория и калия, в гравиразведке - трехкоординатный вектор силы тяжести, и т.п. Если на какой-либо площади проведена съемка нескольких видов геофизики, то их результаты также могут рассматриваться в совокупности, как многомерная функция физических параметров данной геологической среды.По определениям (18.1.1) двумерные функции и сигналы, равно как и многомерные, имеют бесконечную протяженность по координатам. На практике мы всегда имеем дело с конечными координатами наших данных. Учитывая это, будем считать, что значения наших сигналов за пределами определенных координат равны нулю.
Отметим некоторые двумерные последовательности (функции, сигналы), имеющие специальные названия.
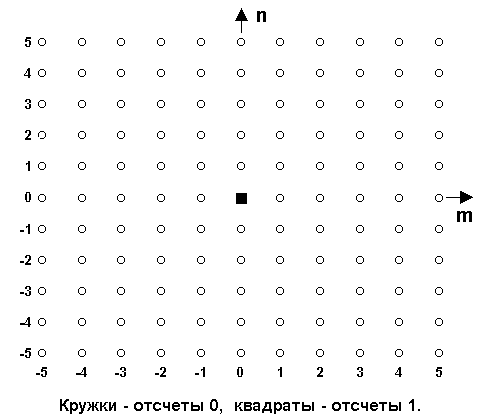
Двумерный единичный импульс
d(nDx,mDy) = dn,m или единичный отсчет:d
n,m = 1, при n = m = 0.= 0, при n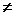
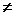 0.
0.
d
n,m = dn dm,где
dn, dm - одномерные единичные импульсы (импульсы Кронекера) по координатам n и m. Стилизованное графическое представление двумерного единичного импульса приведено на рис. 18.1.2.Произвольное расположение двумерного единичного импульса по координатам n
1, m1 соответственно записывается в виде: d((n-n1)Dx,(m-m1)Dy) = dn-n1,m-m1. Попутно напомним, что математическая запись импульса Кронекера обозначает не единичный отсчет, а функцию, определяющую место положения единичного отсчета и нулевые значения по остальным координатам (аргументам).
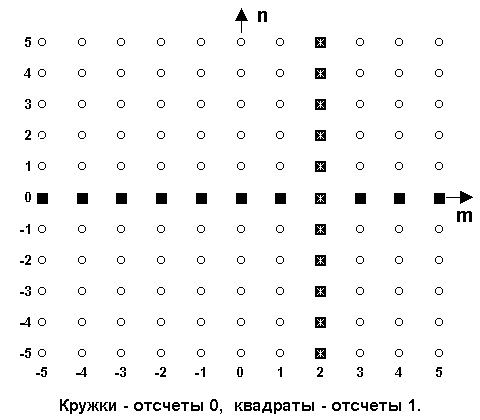 |
Двумерный линейный импульс представляет собой последовательность единичных отсчетов по одной координате: s(n,m) = d(n) или s(n,m) = d(m). На рис. 18.1.3 приведены два двумерных линейных импульса, первый - по координате m = 0: s(n,m) = d(m), и второй импульс по координате n = 2: s(n,m) = d(n-2).Очевидно, что для P-мерных случаев точно таким же образом могут быть определены P-мерные единичные импульсы, P-мерные линейные импульсы, P-мерные площадные импульсы и т.д., хотя понятие импульса, заимствованное из теории одномерных сигналов, здесь несколько не к месту. |
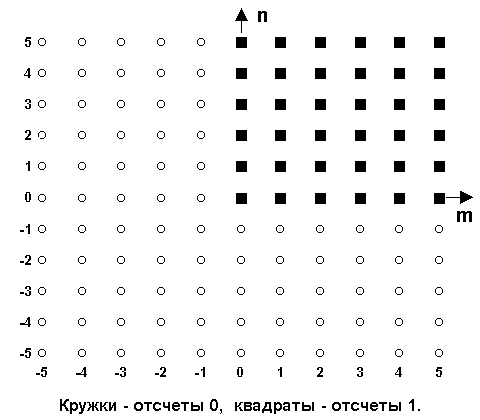
Двумерная единичная ступенька u(n,m), представленная на рис. 18.1.4, определяется выражением:
u(n,m) = 1, при n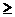 0 и m
0 и m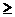
= 0, в остальных случаях.
u(n,m) = u(n) u(m),
где u(j) представляют собой единичные ступеньки соответственно по координатам n и m: u(j)=1 при j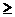 0, u(j)=0 при j<0. Двумерная единичная ступенька отлична от нуля в одном квадранте (n,m)- плоскости.
0, u(j)=0 при j<0. Двумерная единичная ступенька отлична от нуля в одном квадранте (n,m)- плоскости.
Экспоненциальная последовательность
: s(n,m) = anbm, -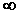 < n,m <
< n,m <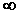 , где а и b в общем случае комплексные числа. При а = exp(jw1), b = exp(jw2), |а|=1, |b|=1:
, где а и b в общем случае комплексные числа. При а = exp(jw1), b = exp(jw2), |а|=1, |b|=1:
s(n,m) = exp(jnw1+jmw2) = cos(nw1+mw2)+jsin(nw1+mw2).
Экспоненциальные последовательности, как и в одномерном случае, являются собственными функциями двумерных линейных систем, инвариантных к сдвигу.
Разделимые последовательности.
Разделимой называют последовательность, которую можно представить в виде произведения одномерных последовательностей. Так, для двумерной разделимой последовательности:s(n,m) = s(n) s(m).
Разделение возможно для немногих практических сигналов. Однако любое двумерное множество с конечным числом ненулевых отсчетов разлагается на конечную сумму разделимых последовательностей:
s(n,m) =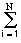 siЧ n(n) siЧ m(m),
siЧ n(n) siЧ m(m),
где N- число ненулевых строк или столбцов массива. В крайнем случае, для этого достаточно выразить s(n,m) в виде суммы отдельных строк:
s(n,m) =  s(n,i) d(m-i). (18.1.2)
s(n,i) d(m-i). (18.1.2)
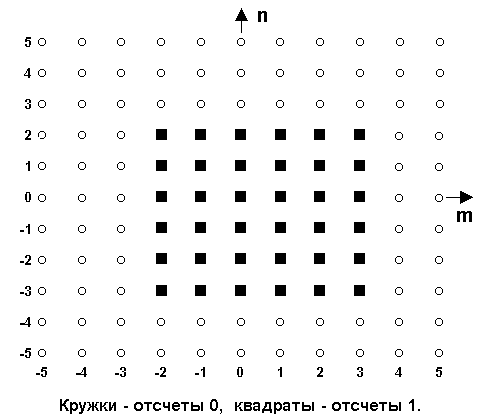
Конечные последовательности. Важным классом сигналов являются последовательности конечной протяженности, для которых сигнал равен нулю вне определенной области, называемой опорной областью сигнала. На рис.18.1.5 условно представлена двумерная последовательность конечной протяженности, значения которой отличны от нулевых только внутри ограниченной прямоугольной области -3 n n 2, -2 2, -2 m m . Опорная область сигнала может быть произвольной формы и выходить за пределы сигнала, частично включая нулевые отсчеты. Отсчеты за пределами опорной области считаются равными нулю. . Опорная область сигнала может быть произвольной формы и выходить за пределы сигнала, частично включая нулевые отсчеты. Отсчеты за пределами опорной области считаются равными нулю.
|
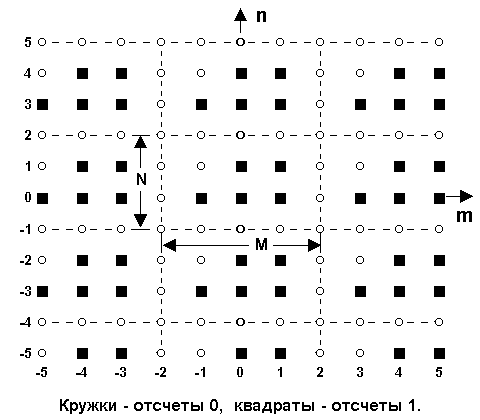
Периодические последовательности. Двумерные последовательности могут быть периодическими, регулярно повторяющимися в пространстве. Последовательность, удовлетворяющая условиям:
s(n,m+M) = s(n,m),
s(n+N,m) = s(n,m), (18.1.3)
обладает периодичностью в двух направлениях, по n и по m. Значения М и N называют интервалами периодичности сигнала соответственно по координатам m и n (горизонтальными и вертикальными интервалами периодичности). Прямоугольная форма области периода (пример на рис.18.1.6) наиболее удобна при обработке данных, но не является единственно возможной.
Для двумерных последовательностей условия (18.1.3) могут рассматриваться как частный случай общих условий периодичности:
s(n+N1, m+M1) = s(n,m), (18.1.4)
s(n+N2, m+M2) = s(n,m),
D = N1M2 - N2M1  0.
0.
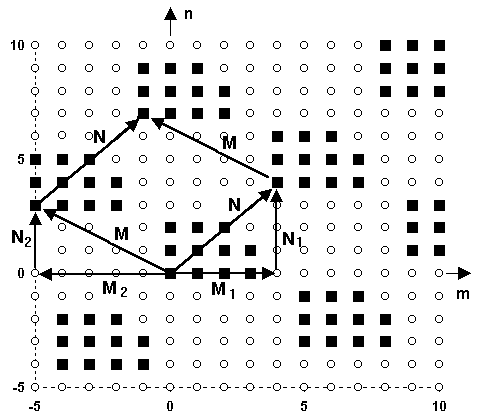
Упорядоченные пары (N
1,M1) и (N2,M2) представляют собой смещения от отсчетов одного периода к соответствующим отсчетам других периодов и могут рассматриваться как векторы N и M, которые образуют области периодов в форме параллелограмма. Линейная независимость векторов обеспечивается при ненулевом определителе D, а количество отсчетов в пределах периода равно |D|. Пример периодической последовательности с векторами (4,4) и (3,-5) приведен на рис. 18.1.7.Понятие периодичности можно обобщить на многомерные сигналы. P-мерный сигнал s(
s( ) = s(
) = s( +
+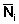 ), i = 1,2,3, ... ,P.
), i = 1,2,3, ... ,P. 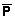
Столбцы векторов
Ni образуют матрицу периодичности N размером P х P. Векторы периодичности матрицы линейно независимы при наличии у матрицы ненулевого определителя. Абсолютное значение определителя равно числу отсчетов в периоде. Последовательность s( ) прямоугольно периодична для случаев диагональной матрицы N. Если функция s(
) прямоугольно периодична для случаев диагональной матрицы N. Если функция s( ) периодична с матрицей периодичности N, то для любого целочисленного вектора Р имеет место s(
) периодична с матрицей периодичности N, то для любого целочисленного вектора Р имеет место s( +
+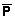
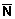 ) = s(
) = s( ), и матрица PN также будет матрицей периодичности для s(
), и матрица PN также будет матрицей периодичности для s( ). Отсюда следует, что любая многомерная периодическая последовательность имеет не единственную матрицу периодичности.
). Отсюда следует, что любая многомерная периодическая последовательность имеет не единственную матрицу периодичности.
18.2. Двумерные системы.
Системы осуществляют преобразование сигналов. Формализованная система - это оператор (операция) отображения входного сигнала на выходной: z(x,y) = Т[s(x,y)].
Базовыми операциями
в системах, комбинациями которых осуществляются преобразования, являются операции скалярного умножения, сдвига и сложения:z(n,m) = c s(n,m),
z(n,m) = s(n-N,m-M),
z(n,m) = s(n,m)+u(n,m).
Используя базовые операции, любую двумерную последовательность можно разложить на сумму взвешенных двумерных единичных импульсов:
s(n,m) =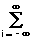
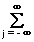 s(i,j) d(n-i,m-j). (18.2.1)
s(i,j) d(n-i,m-j). (18.2.1)
Обобщением скалярного умножения является пространственное маскирование:
z(n,m) = cn,m s(n,m). (18.2.2)
Правая часть равенства (18.2.2) представляет собой поэлементное произведение входного сигнала на совокупность чисел с
n,m.Кроме линейных операций в системах используются также безынерционные нелинейные преобразования с независимым нелинейным воздействием на значения отсчетов входной последовательности. Пример операции - возведение в квадрат:
zn,m = (sn,m)2.
Линейные системы.
Система считается линейной при выполнении двух условий:1. Пропорциональное изменение входного сигнала вызывает пропорциональное изменение выходного сигнала.
2. Суммарный сигнал двух входных последовательностей дает суммарный сигнал двух соответствующих выходных последовательностей.
Другими словами, если оператор Т[s(x,y)] описывает линейную систему и имеет место z(x,y) = Т[s(x,y)], q(x,y) = Т[u(x,y)], то Т[as(x,y)+bu(x,y)] = az(x,y)+bq(x,y). Линейные системы подчиняются принципу суперпозиции сигналов.
В выражении (18.2.1) значения s(i,j) можно рассматривать как скалярные множители для соответствующих единичных импульсов. Применяя оператор преобразования Т[.] к левой и правой части (18.2.1), получаем:
Т[s(n,m)] = у(n,m) = 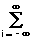
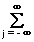
z(n,m) = 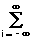
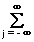 s(i,j) hij(n,m), (18.2.3)
s(i,j) hij(n,m), (18.2.3)
где h
ij(n,m) - отклик системы в точке (n,m) на единичный импульс в точке (i,j). Если импульсный отклик hij(n,m) определен для всех точек (i,j), то отклик системы на произвольный многомерный сигнал, как и для одномерных систем, находится с помощью суперпозиции.Инвариантность к сдвигу. Система инвариантна к сдвигу, если сдвиг входной последовательности приводит к такому же сдвигу выходной последовательности:
Т[s(n-N,m-M)] = z(n-N,m-M).
Линейность и инвариантность к сдвигу являются независимыми свойствами системы. Так, пространственное маскирование линейно, но не инвариантно к сдвигу, а безынерционные операторы нелинейны, но инвариантны к сдвигу.
В дальнейшем ограничимся рассмотрением только систем, широко распространенных при решении практических задач - линейных и инвариантных к сдвигу (ЛИС-системы).
Импульсный отклик на произвольно расположенный входной импульс, как следует из выражения (18.2.3), описывается выражением:
hij(n,m) = T[d(n-ni,m-mj)].
Для частного случая i = j = 0 имеем:
ho(n,m) = T[d(n,m)].
Используя принцип инвариантности к сдвигу, получим:
hij(n,m) = ho(n-i,m-j) = h(n-i,m-j), (18.2.4)
т.e. импульсный отклик на произвольно расположенный входной импульс равен сдвинутому импульсному отклику на входной импульс, расположенный в начале координат.
Двумерная свертка.
Подставляя (18.2.4) в выражение (18.2.3), получаем:z(n,m) = Si Sj s(i,j) h(n-i,m-j). (18.2.5)
Двумерная дискретная свертка (18.2.5), является аналогом одномерной дискретной свертки. При замене переменных n-i = k, m-j = l, получим:
z(n,m) = Sk Sl h(k,l) s(n-k,m-l), (18.2.5')
т.е. двумерная свертка коммутативна, как и одномерная. В такой же мере она обладает свойством ассоциативности по отношению к последовательности операций свертки нескольких функций (результат не зависит от порядка свертки) и свойством дистрибутивности по отношению к операции свертки с суммой функций (результат аналогичен сумме сверток с каждой функцией). Эти свойства определяют и основное свойство двумерных (и многомерных) линейных систем при их параллельном и/или последовательном соединении – результирующая система также является линейной.
Для упрощения символьного аппарата двумерную свертку обозначают индексом (
**):z(n,m) = h(k,l) ** s(n-k,m-l).
При обобщении этого выражения на многомерные системы, в векторной форме:
z( )= h(
)= h(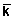 ) ** s(
) ** s( -
-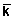 ).
).
Разделимые системы.
Если импульсный отклик системы может быть разделен:h(k,l) = h(k) h(l), (18.2.6)
то выражение (18.2.5') принимает вид:
z(n,m) = Sk h(k) Sl h(l) s(n-k,m-l), (18.2.7)
или: z(n,m) =
Sk h(k) g(n-k,m), g(n-k,m) = Sl h(l) s(n,m-l).Массив g(n,m) вычисляется одномерной сверткой столбцов массива s(n,m) при n = const (сечения массива по координатам n) с откликом h(l), с последующим вычислением выходного массива z(n,m) одномерной сверткой строк g(n,m) при m = const с откликом h(k). Результат не изменится, если сначала выполнять свертку по строкам, а затем по столбцам. Система с откликом вида (18.2.6) называется разделимой. Отметим, что в разделимой системе входной и выходной сигнал не обязаны быть разделимыми.
Аналогичные разделимые системы могут существовать и в многомерном варианте
.Устойчивость системы.
Интерес для практики представляют только устойчивые системы, обеспечивающие определенный конечный результат системной операции на конечные входные сигналы. Необходимым и достаточным условием устойчивости системы является абсолютная суммируемость ее импульсного отклика: Sk Sl |h(k,l)| <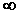 .
.
Специальные двумерные системы.
На практике используются также системы с несколькими входами и/или выходами.Допустим, система имеет i-входы и j-выходы, линейна и инвариантна к сдвигу по переменной t. Если на i-вход системы поступает одномерный единичный импульс
di(t) при нулевых сигналах на остальных входах, то j-выходные сигналы будут импульсным откликом системы hij(t). При известном полном ансамбле значений hij для всех i-входов, для произвольной комбинации входных сигналов si(t) сигнал на j-выходе будет определяться выражением:zj(t) = Si Sk hij(k) si(t-k). (18.2.8)
18.3. Частотные характеристики сигналов и систем.
Частотный отклик системы.
Допустим, что двумерная ЛИС-система имеет импульсный отклик h(kDx,lDy). Подадим на вход системы сигнал вида комплексной синусоиды:s(n,m) = exp(jnDxЧ wx+jmDyЧ wy),
где
wx и wy – значения частоты сигнала соответственно по координатам x и y. Принимая Dx = 1, Dy = 1 и выполняя двумерную свертку (18.2.5), получаем:z(n,m) =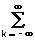
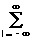 h(k,l) exp[jЧ wxЧ (n-k)+jЧ wyЧ (m-l)] =
h(k,l) exp[jЧ wxЧ (n-k)+jЧ wyЧ (m-l)] =
= exp(jnЧ wx+jmЧ wy) 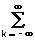
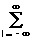 h(k,l) exp(-jkЧ wx-jlЧ wy) = H(wx,wy) exp(jnЧ wx+jmЧ wy).
h(k,l) exp(-jkЧ wx-jlЧ wy) = H(wx,wy) exp(jnЧ wx+jmЧ wy).
H(wx,wy) = 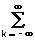
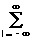 h(k,l) exp(-jkЧ wx-jlЧ wy). (18.3.1)
h(k,l) exp(-jkЧ wx-jlЧ wy). (18.3.1)
Таким образом, выходной сигнал представляет собой комплексную синусоиду с теми же значениями частоты, что и у входного сигнала, с изменением амплитуды и фазы за счет комплексного множителя H(
wx,wy), который носит название частотного отклика (частотной характеристики) системы. Для дискретных сигналов частотный отклик периодичен с периодом 2p по обеим частотным переменным:H(wx+2pk,wy+2pl) = H(wx,wy).
Пример расчета частотного отклика системы.
Определить частотную характеристику системы с импульсным откликом:
h(0,0) = 0.25, h(0,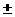 1) = 0.125, h(
1) = 0.125, h(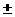 1,0) = 0.125, h(
1,0) = 0.125, h(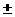 1,
1,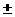 1) = 0.0625.
1) = 0.0625.
Частотный отклик:
H(
wx,wy) =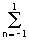
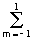 h(n,m)exp(-jnwx-jmwy) = 0.25+0.125[exp(-jwx)+exp(jwx)+exp(-wy)+exp(jwy)]+
h(n,m)exp(-jnwx-jmwy) = 0.25+0.125[exp(-jwx)+exp(jwx)+exp(-wy)+exp(jwy)]+
+0.0625[exp(-j
wx-jwy)+exp(-jwx+jwy)+exp(jwx-jwy)+exp(jwx+jwy)] = 0.25(1+cos wx)(1+cos wy).Система является примером двумерного фильтра нижних частот. Частотный отклик системы на плоскости (
wx,wy), приведенный на рис. 18.3.1, имеет осевую симметрию с коэффициентом передачи 1 в центре (wx=0, wy=0) со спадом до нуля при wx=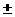 p и wy=
p и wy=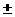 p.
p.
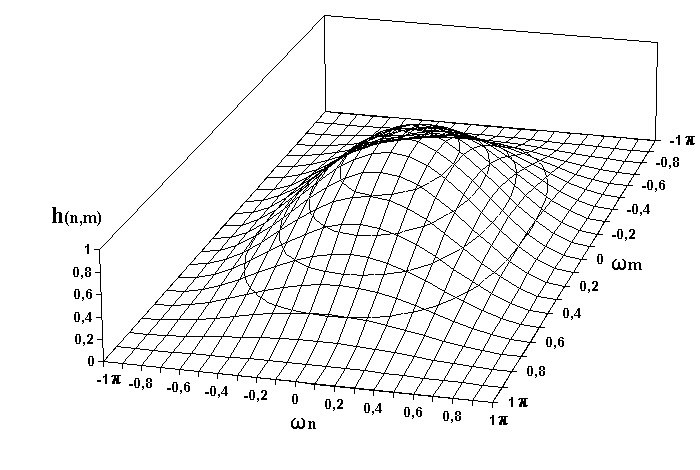
Рис. 18.3.1. Частотная характеристика ФНЧ.
При разделимости импульсного отклика частотный отклик многомерных систем также является разделимой функцией:
h(k,l)= q(k)g(l) Ы Q(wx)G(wy)= H(wx,wy)
Q(wx) = Sk q(k) exp(-jkЧ wx). G(wy) = Sl g(l) exp(-jlЧ wy).
Импульсный отклик системы.
Выражение (18.3.1), по существу, описывает разложение функции Н(wx,wy) в двумерный рад Фурье с коэффициентами разложения в виде отсчетов импульсного отклика h(k,l), т.е. прямое преобразование Фурье. Очевидно, что обратным преобразованием Фурье с интегрированием в пределах одного периода из частотного отклика H(wx,wy) можно получить импульсный отклик системы:h(k,l) = 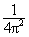
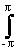
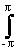 H(wx,wy) exp(jkwx+jlwy) dwxdwy. (18.3.2)
H(wx,wy) exp(jkwx+jlwy) dwxdwy. (18.3.2)
Пример расчета импульсного отклика фильтра.
Определить импульсный отклик идеального фильтра низких частот с прямоугольной частотной характеристикой вида: H(
wx,wy) = 1 при |wx| a<p, |wy|
a<p, |wy| b<p; H(wx,wy) = 0 в остальных случаях.
b<p; H(wx,wy) = 0 в остальных случаях.
Импульсный отклик: h(k,l) = 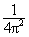
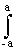
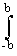
Система разделима: h(k,l)= 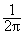
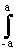
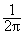
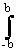 exp(jlwy) dwy=
exp(jlwy) dwy= 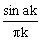 Ч
Ч 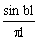 .
.
Пример расчета неразделимого импульсного отклика.
Определить импульсный отклик идеального кругового фильтра нижних частот:
H(
wx,wy) = 1 при wx2+wy2 <R2<p2; H(wx,wy) = 0 в остальных случаях.Вычисления по круговой области целесообразно выполнять в полярных координатах:
w =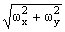 ,
,
j =
arctg(wy/wx), f = arctg(m/n), при этом выражение 18.3.2 перепишется в следующем виде:h(n,m) = 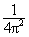
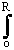
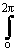
= 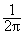
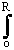
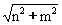 ) dw =
) dw = 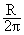 J1(R
J1(R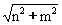 ) /
) /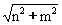 ,
,
где J
o(…), J1(…)- функции Бесселя 1-го рода 0-го и 1-го порядков соответственно.На рис. 18.3.2 приведена пространственная форма импульсного отклика фильтра, расчет которой проведен при R = 1 с ограничением по N = 10 и M = 10, и сечения отклика по координате m.
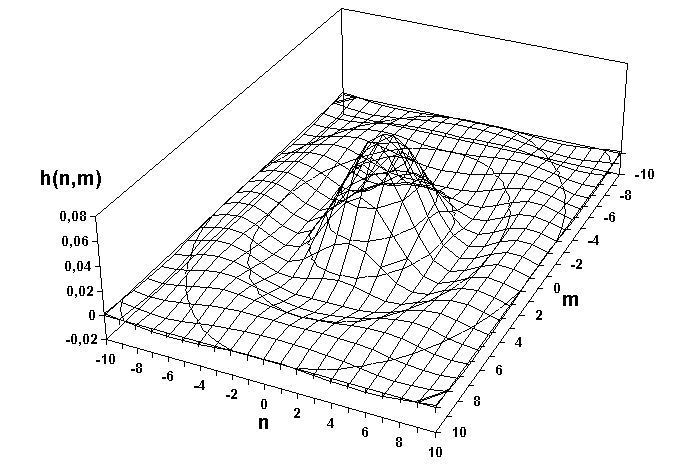
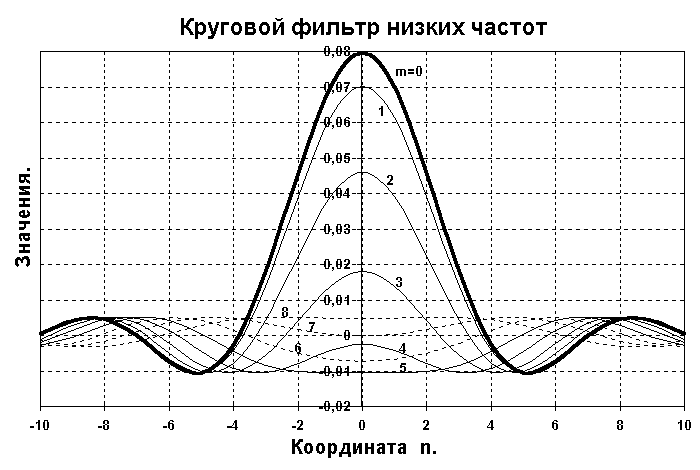
Рис. 18.3.2. Круговой низкочастотный фильтр (справа - сечения по координате m).
Свойства двумерного преобразования Фурье.
Вышеприведенные преобразования импульсного отклика в частотный отклик и наоборот представляют собой двумерные дискретные преобразования Фурье с прямоугольным растром дискретизации информации, эквивалентные одномерным преобразованиям. На двумерные преобразования с прямоугольным растром переносятся и другие свойства одномерных систем. В частности:1. Фурье-преобразования сигналов.
S(wx,wy) = Sn Sm s(n,m) exp(-jnwx-jmwy). (18.3.3)
s(n,m) =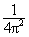
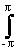
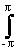 S(wx,wy) exp(jnwx+jmwy) dwxdwy. (18.3.4)
S(wx,wy) exp(jnwx+jmwy) dwxdwy. (18.3.4)
2. Теорема о свертке.
z(n,m) = h(n,m) ** s(n,m) Ы H(wx,wy) S(wx,wy) = Z(wx,wy).
z(n,m) = c(n,m) s(n,m) Ы C(wx,wy) ** S(wx,wy) = Z(wx,wy).
3. Основные свойства Фурье-преобразования.
1) Линейность (в том числе для любых комплексных чисел a и b):
а
Ч s(n,m)+bЧ z(n,m) Ы aS(wx,wy)+bZ(wx,wy).2) Пространственный сдвиг:
s(n-N,m-M) Ы S(wx,wy) exp(-jNwx-jMwy).
3) Дифференцирование:
dS(wx,wy)/dwx Ы -jn s(n,m),
dS(wx,wy)/dwy Ы -jm s(n,m),
d2S(wx,wy)/(dwx dwy) Ы -nm s(n,m).
4) Комплексное сопряжение:
х*(n,m)
Ы S*(-wx,-wy).Вещественная и мнимая части Фурье-образов последовательностей s(n,m):
S(wx,wy) = S*(-wx,-wy).
Re [S(wx,wy)] = Re [S(-wx,-wy)].
Im [S(wx,wy)] = -Im [S(-wx,-wy)].
5) Теорема Парсеваля:
S
n Sm s(n,m) s*(n,m) =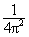
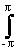
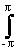 S(wx,wy) S*(wx,wy) dwx dwy.
S(wx,wy) S*(wx,wy) dwx dwy.
В частности, при s(n,m) = s(n,m):
S
n Sm |s(n,m)|2 =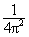
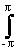
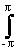 |S(wx,wy)|2 dwx dwy,
|S(wx,wy)|2 dwx dwy,
где левая часть уравнения представляет собой полную энергию дискретного сигнала s(n,m), a функция |S(
wn,wm)|2 - спектральную плотность энергии сигнала.18.4. Дискретизация двумерных сигналов [9].
Прямоугольный растр дискретизации.
Из способов обобщения одномерной периодической дискретизации на двумерный случай наиболее простым является периодическая дискретизация в прямоугольных координатах:s(n,m) = sa(nDx,mDy),
где
Dx и Dy - горизонтальный и вертикальный интервалы дискретизации двумерного непрерывного сигнала sa(x,y) с непрерывными координатами x и y. Ниже значения Dx и Dy, как и в одномерном случае, принимаются равными 1.Дискретизация двумерного, а в общем случае и многомерного сигнала, также приводит к периодизации его спектра и наоборот. Сохраняется также и условие информационной равноценности координатного и частотного представлений дискретного сигнала при равном количестве точек дискретизации в главных диапазонах сигнала. Для прямоугольной дискретизации связь фурье-преобразований непрерывного и дискретного сигналов устанавливается аналогично одномерной дискретизации.
Интегральные преобразования Фурье
аналоговых сигналов в непрерывной шкале частот Wx и Wy: Sa(Wx,Wy) =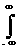
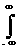 sa(x,y) exp(-jWxx-jWyy) dxdy. (18.4.1)
sa(x,y) exp(-jWxx-jWyy) dxdy. (18.4.1)
sa(x,y) =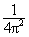
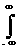
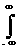 Sa(Wx,Wy) exp(jWxx+jWyy) dWxdWy. (18.4.2)
Sa(Wx,Wy) exp(jWxx+jWyy) dWxdWy. (18.4.2)
Дискретные преобразования Фурье:
S(k,l) =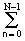
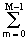 s(n,m) exp(-jn2pk/N-jm2pl/M), (18.4.3)
s(n,m) exp(-jn2pk/N-jm2pl/M), (18.4.3)
S(k,l) =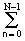 exp(-jn2pk/N)
exp(-jn2pk/N) 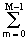 s(n,m) exp(-jm2pl/M), (18.4.3')
s(n,m) exp(-jm2pl/M), (18.4.3')
s(n,m) =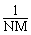
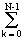
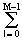 S(k,l) exp(-jn2pk/N-jm2pl/M). (18.4.4)
S(k,l) exp(-jn2pk/N-jm2pl/M). (18.4.4)
s(n,m) =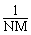
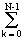 exp(-jn2pk/N)
exp(-jn2pk/N) 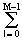 S(k,l) exp(-jm2pl/M). (18.4.4')
S(k,l) exp(-jm2pl/M). (18.4.4')
Выражения (18.4.3') и (18.4.4') показывают, что двумерное ДПФ по прямоугольному растру дискретизации данных может вычисляться с помощью одномерных последовательных ДПФ. Вторые суммы выражений являются одномерными ДПФ сечений функций s(n,m) и S(k,l) по линиям n и k соответственно, а первые - одномерными ДПФ вычисленных функций в сечениях по m и l. Другими словами, исходные матрицы значений s(n,m) и S(k,l) пересчитываются сначала в промежуточные матрицы с ДПФ по строкам (или по столбцам), а промежуточные - в окончательные с ДПФ по столбцам (или соответственно по строкам).
Интерполяционный ряд восстановления двумерного сигнала.
Если непрерывный сигнал sa(x,y) является сигналом с ограниченным спектром, а периоды дискретизации выбраны достаточно малыми и спектры соседних периодов не перекрываются:Sa(Wx,Wy) = 0 при |Wx|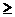 p/Dx, |Wy|
p/Dx, |Wy|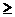 p/Dx,
p/Dx,
то, как и в одномерном случае, сигнал s
a(x,y) может быть восстановлен по дискретному сигналу с использованием двумерного аналога ряда Котельникова-Шеннона: sa(x,y) = Sn Sm s(n,m)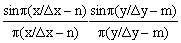 . (18.4.5)
. (18.4.5)
Сигнал с неограниченным спектром также может быть дискретизирован, однако в этом случае имеет место наложение спектров в смежных периодах, при этом высокие частоты, большие частоты Найквиста, будут "маскироваться", как и в одномерном случае, под низкие частоты главного периода. Эффект "отражения" от границ периода дает еще более сложную картину вследствие интерференции частот, отраженных по разным координатам.
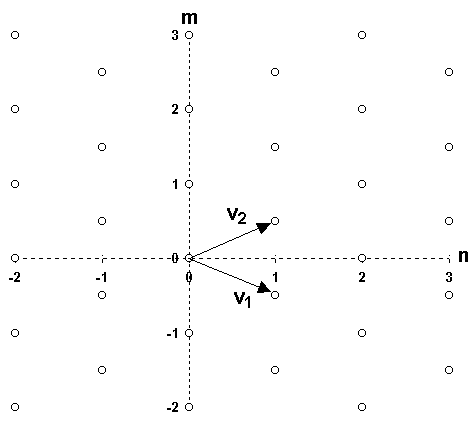
Произвольный растр дискретизации.
Понятие прямоугольной дискретизации обобщается на произвольный растр дискретизации с линейно независимыми векторами v1 = (v11,v21)T и v2 = (v12,v22)T, где T - индекс транспонирования (рис. 18.4.1). Координаты двумерного периодического множества отсчетов на плоскости (x,y):x = v11n + v12m,
y = v21n + v22m.
С использованием векторных обозначений:
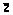 =
=

где 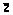
 =(n,m)T,
=(n,m)T,  =(v1|v2)- матрица дискретизации. Определитель матрицы
=(v1|v2)- матрица дискретизации. Определитель матрицы  не равен нулю, если вектора v1 и v2 линейно независимы. При дискретизации непрерывного сигнала sa(x,y) матрицей
не равен нулю, если вектора v1 и v2 линейно независимы. При дискретизации непрерывного сигнала sa(x,y) матрицей  формируется дискретный сигнал:
формируется дискретный сигнал:
s( ) Ь sa(
) Ь sa(
 ).
).
Двумерное интегральное преобразование Фурье
непрерывного сигнала по непрерывному вектору = (W1,W2)T:
= (W1,W2)T:
Sa( ) =
) =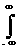 sa(
sa(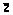 ) exp(-j
) exp(-j T
T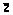 ) d
) d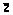 , (18.4.6)
, (18.4.6)
sa(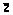 ) =
) =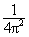
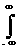 Sa(
Sa( ) exp(j
) exp(j T
T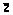 ) d
) d , (18.4.7)
, (18.4.7)
Данные интегралы являются двойными, поскольку дифференциалы d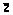 и d
и d являются векторами.
являются векторами.
Преобразование Фурье дискретного сигнала:
S( ) = Sn s(
) = Sn s( ) exp(-j
) exp(-j T
T ), (18.4.8)
), (18.4.8)
s( ) =
) =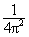
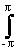 S(
S( ) exp(j
) exp(j T
T ) d
) d . (18.4.9)
. (18.4.9)
где: 
Выражение s( ) может быть получено дискретизацией выражения s
) может быть получено дискретизацией выражения s
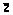 ) (18.4.7):
) (18.4.7):
s( ) = sa(
) = sa(
 ) =
) =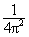
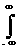 Sa(
Sa( ) exp(j
) exp(j T
T
 ) d
) d .
.
После подстановки в это выражение значения 

 T, получаем:
T, получаем:
s( ) =
) = 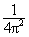
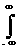
 Sa(
Sa( /
/ T) exp(j
T) exp(j Т
Т ) d
) d .
.
Или, с учетом периодичности по квадратным областям плоскости
s( ) =
) = 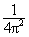
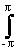

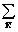 Sa((
Sa(( -2p
-2p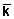 )/
)/ T) exp(j
T) exp(j Т
Т ) d
) d , (18.4.10)
, (18.4.10)
где 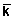 - вектор целочисленных значений периодов дискретизированной функции по осям
- вектор целочисленных значений периодов дискретизированной функции по осям
S( ) =
) =
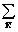 Sa((
Sa(( -2p
-2p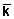 )/
)/ T),
T),
S(
 T) =
T) = 
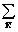 Sa(
Sa( -
-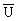
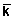 ), (18.4.11)
), (18.4.11)
где  - матрица периодичности:
- матрица периодичности:
 Т
Т = 2p
= 2p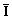 , (18.4.12)
, (18.4.12)
которой задаются два линейно независимых вектора периодичности спектра, 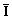 - единичная матрица 2 х 2. Выражение (18.4.11) определяет связь между преобразованиями Фурье дискретных и аналоговых сигналов.
- единичная матрица 2 х 2. Выражение (18.4.11) определяет связь между преобразованиями Фурье дискретных и аналоговых сигналов.
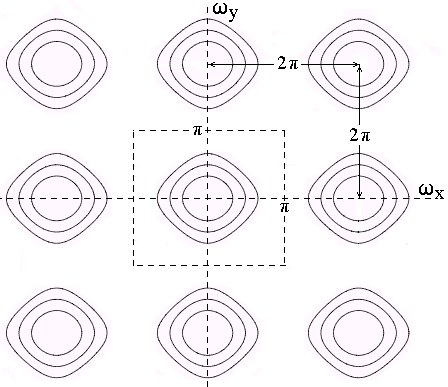
Как и в одномерном случае, интервалы дискретизации
Dx и Dy определяют главный период двумерного спектра соответственно по осям wx и wy и частоты Найквиста: wxN = p/Dx и wyN = p/Dy. Спектр дискретного сигнала также является периодическим продолжением спектра аналогового сигнала. Для исключения искажений спектра (наложения спектров боковых периодов на главный период) предельные частоты сигнала должны быть меньше частот Найквиста. На рис. 18.4.2 приведен пример центральной части спектра дискретного сигнала при Dx=1 и Dy=1.В случае прямоугольной дискретизации:
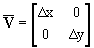 , det
, det  = DхDу, (18.4.13)
= DхDу, (18.4.13)
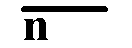 . (18.4.14)
. (18.4.14)
Интерполяция дискретных сигналов.
Для сигнала с ограниченным спектром изменением матрицы дискретизации можно подобрать матрицу периодичности
можно подобрать матрицу периодичности 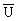 таким образом, чтобы в правой части выражения (18.4.11) не было перекрытия спектров. Тогда для значений по точкам
таким образом, чтобы в правой части выражения (18.4.11) не было перекрытия спектров. Тогда для значений по точкам 
 T области С главного периода спектра выражение (18.4.11) упрощается:
T области С главного периода спектра выражение (18.4.11) упрощается:
S(
 T) = Sa(
T) = Sa( ) / |det
) / |det  |. (18.4.15)
|. (18.4.15)
Sa( ) = |det
) = |det  | S(
| S(
 T) = |det
T) = |det  | S(
| S( ),
),  О С. (18.4.16)
О С. (18.4.16)
Из выражения (18.4.16) следует, что при корректной дискретизации непрерывной двумерной функции ее спектр с точностью до нормировочного множителя |det  | может быть восстановлен по спектру дискретной функции. Соответственно, выполнив обратное преобразование Фурье левой и правой части равенства (18.4.16), получим уравнение восстановления непрерывной функции по ее дискретному варианту (многомерный аналог интерполяционного ряда Котельникова-Шеннона):
| может быть восстановлен по спектру дискретной функции. Соответственно, выполнив обратное преобразование Фурье левой и правой части равенства (18.4.16), получим уравнение восстановления непрерывной функции по ее дискретному варианту (многомерный аналог интерполяционного ряда Котельникова-Шеннона):
sa(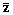 ) =
) = 
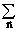 s(
s(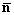 )
)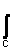 exp(j
exp(j T (
T (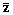 -
-
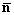 )) d
)) d .
.
sa(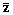 ) =
) = 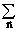 s(
s(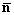 ) f(
) f(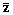 -
-
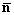 ), (18.4.17)
), (18.4.17)
где f(..) – интерполяционная функция:
f(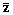 -
-
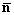 ) =
) = 
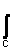 exp(j
exp(j T (
T (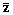 -
-
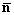 )) d
)) d . (18.4.18)
. (18.4.18)
Все приведенные векторные уравнения могут быть обобщены на Р-мерные функции с заменой константы 4
p2 там, где она встречается, на (2p)P.Прямоугольный и гексагональный растры дискретизации.
В принципе, сигнал с ограниченным спектром можно представить по различным растрам дискретизации. Выбор растра обычно производят из условия минимальной плотности отсчетов на плоскости, т.е. минимизацией величины |det |, при котором обеспечивается отсутствие наложений для частот анализируемых сигналов.
|, при котором обеспечивается отсутствие наложений для частот анализируемых сигналов.
На практике для двумерных сигналов используют, как правило, только два варианта растров дискретизации - прямоугольный и гексагональный. Прямоугольному варианту соответствуют диагональные матрицы дискретизации и периодичности (18.4.13-14). Для гексагональной дискретизации, пример которой приведен на рис. 18.4.1, в частном случае при
Dt = Dх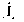 каждый отсчет располагается на равном расстоянии от шести ближайших отсчетов, при этом матрицы дискретизации:
каждый отсчет располагается на равном расстоянии от шести ближайших отсчетов, при этом матрицы дискретизации:
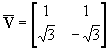 ,
, 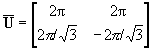 .
.
Допустим, имеем сигнал с частотным спектром, ограниченным круговой областью частот
wr:Sa(wх,wу) = 0 при wх2+wу2 > wr2.
Круговая область частот вписывается без перекрытий в квадрат со стороной 2
wr или в шестиугольник со стороной 2wr/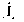 . Матрицы дискретизации:
. Матрицы дискретизации: пр =
пр =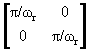 , det
, det  = p2/wr2,
= p2/wr2,
 гекс =
гекс =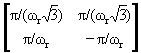 , det
, det  = 2p2/(wr2
= 2p2/(wr2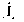 ).
).
Поскольку плотность отсчетов пропорциональна 1/|det |, то отсюда следует, что для представления одного и того же сигнала гексагональный растр дискретизации требует на 13.4% меньше отсчетов по сравнению с прямоугольным. Эффективность "гексагональной" матрицы возрастает при увеличении размерности сигнала. Так, при 4-мерном сигнале для "гексагональной" матрицы требуется в 2 раза меньше отсчетов, чем для "прямоугольной".
|, то отсюда следует, что для представления одного и того же сигнала гексагональный растр дискретизации требует на 13.4% меньше отсчетов по сравнению с прямоугольным. Эффективность "гексагональной" матрицы возрастает при увеличении размерности сигнала. Так, при 4-мерном сигнале для "гексагональной" матрицы требуется в 2 раза меньше отсчетов, чем для "прямоугольной".
18.5. Многомерный спектральный анализ [9].
Периодические последовательности.
Двумерная последовательность s(n,m) прямоугольно периодична, еслиsп(n,m) = s(n,n+M) = s(n+N,m)
для всех (n,m) при целочисленных значениях N и M. Минимальные значения N и M, при которых выполняется данное равенство, называют горизонтальным и вертикальным периодами функции s
п(..), которыми ограничивается прямоугольная область RN,M главного периода, содержащая NM независимых отсчетов: 0 n
n N-1, 0
N-1, 0 m
m M-1.
M-1.
Последовательность s
п(n,m) с периодами N и M можно представить в виде конечной суммы (ряда Фурье) комплексных синусоид с кратными частотами: sп(n,m) =(1/NM)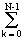
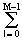 Sп(k,l) exp(j2pnk/N+j2pml/M). (18.5.1)
Sп(k,l) exp(j2pnk/N+j2pml/M). (18.5.1)
Sп(k,l) =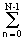
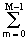 sп(n,m) exp(-j2pnk/N-j2pml/M). (18.5.2)
sп(n,m) exp(-j2pnk/N-j2pml/M). (18.5.2)
Пример.
Разложить в ряд Фурье периодический сигнал: sп
(n,m) = d(n,m), 0 n
n 4, 0
4, 0 m
m 2
2
(единичные импульсы с периодом: N = 5, M = 3).
S
п(k,l) =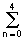
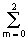 d(n,m) exp(-j2pnk/5-j2pml/3) = 1 для всех k и l, т.е. равномерная частотная характеристика в главном диапазоне. Соответственно сам сигнал может быть записан в виде двумерного ряда Фурье:
d(n,m) exp(-j2pnk/5-j2pml/3) = 1 для всех k и l, т.е. равномерная частотная характеристика в главном диапазоне. Соответственно сам сигнал может быть записан в виде двумерного ряда Фурье:
s
п(n,m) =(1/20)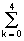
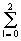 exp(j2pnk/5+j2pml/3).
exp(j2pnk/5+j2pml/3).
Конечные последовательности.
Если s(n,m) представляет собой последовательность конечной протяженности, имеющей опорную область RN,M, то периодическую последовательность sп(n,m) с главным периодом RN,M можно сформировать периодическим продолжением s(n,m): sп(n,m) = 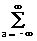
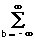 s(n-aN,m-bM),
s(n-aN,m-bM),
s(n, m) = sп(n, m), (n, m) < RN,M.
= 0, в остальных случаях.
Отсюда следует, что любой финитный сигнал может быть полностью определен своим периодическим продолжением и опорной областью.
Аналогично можно записать и для частотной области:
Sп(k, l) = Sa Sb S(k-aN, l-bM).
S(k, l) = Sп(k, l), 0 k
k N, 0
N, 0 l
l M
M
= 0, в остальных случаях.
Отсюда значения s(n,m) и S(k,l) можно вычислить с использованием выражений (18.5.1-2) путем последовательности операций:
s(n,m) Ю sп(n,m) Ы Sп(k,l) Ю S(k,l).
Практически это означает, что для получения ДПФ последовательности конечной протяженности достаточно из выражений (18.5.1-2) для рядов Фурье убрать знак периодичности, при этом следует помнить, что вычисление отсчетов s(..) вне опорной области приведет к вычислению значений не отсчетов s(..), а отсчетов s
п(..) периодического продолжения сигнала s(..).Таким образом:
1. Дискретизация сигнала в пространственной области вызывает периодизацию частотного спектра сигнала.
2. Дискретизация частотного спектра сигнала вызывает периодизацию его пространственного представления.
3. Прямое и обратное ДПФ сигнала ограниченной протяженности автоматически означает периодизацию как его спектра, так и его пространственного представления.
4. Сигналы, ограниченные в пространстве, можно точно отобразить отсчетами их фурье-преобразования.
5. Частотное представление сигнала с ограниченным спектром обратным фурье-преобразованием может быть точно переведено в пространственную область.
6. Ограниченность как пространственного сигнала, так и его спектра является обязательным условием корректного ДПФ, т.к. в противном случае периодизация сигнала может привести к искажению его спектрального и пространственного представления.
Многомерные последовательности. Определение ДПФ для Р-мерной последовательности с опорной областью R
P = {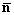 : 0
: 0 ni
ni Ni-1, i=1,2,3, ... ,P} производится введением диагональной матрицы значений Ni:
Ni-1, i=1,2,3, ... ,P} производится введением диагональной матрицы значений Ni:
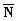 =
=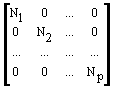 ,
,
при этом P-мерное ДПФ записывается в виде:
S(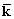 ) =
) =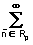 s(
s(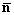 ) exp(-j
) exp(-j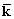 T2p
T2p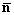 /
/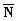 ). (18.5.3)
). (18.5.3)
s(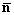 ) =
) =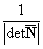
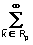 S(
S(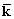 ) exp(j
) exp(j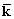 T2p
T2p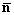 /
/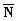 ). (18.5.4)
). (18.5.4)
Кратко рассмотрим особенности многомерных ДПФ (на примере двумерных последовательностей).
ДПФ суммы двух последовательностей с опорной областью на R
N,M равно сумме их ДПФ:аs(n,m)+bz(n,m)
Ы aS(k,l)+bZ(k,l),но при этом все ДПФ должны быть одного размера и этот размер должен быть достаточным, чтобы включить всю опорную область суммарной последовательности аs(n,m)+bz(n,m). Практически это означает, что х(..) и z(..) должны иметь одну и ту же опорную область. Опорная область каждой последовательности при необходимости дополняется нулями.
Операция свертки двух функций в пространственной области отображается операцией умножения фурье-образов функций в частотной области, однако при этом линейная свертка полных пространственных сигналов при ее вычислении через ДПФ в силу периодического продолжения пространственных функций переходит в циклическую свертку (как и для одномерных сигналов). Результат свертки зависит от периодов N и М.
Допустим, что s(n,m) имеет опорную область R
P1,P2, a h(n,m) - RQ1,Q2. Результат линейной свертки:s(n,m) = Sk Sl h(k,l) s(n-k,m-l).
Опорная область последовательности s(n,m):
0 n
n P1+Q1-1, 0
P1+Q1-1, 0 m
m P2+Q2-1.
P2+Q2-1.
Следовательно, наложения периодов результата свертки не произойдет и циклическая свертка в главном частотном диапазоне будет равна линейной свертке при опорной области ДПФ:
N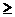 P1+Q1-1, M
P1+Q1-1, M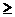 P2+Q2-1.
P2+Q2-1.
Пример.
Заданы последовательности (начало координат в нижнем левом углу): s(n,m) = 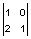
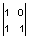 .
.
Вычислить свертку z(n,m) = s(n,m)
** h(n,m).ДПФ размера 2 х 2 для s(n,m). S(0,0) = s(0,0) + s(1,0) + s(0,1) + s(1,1) = 2+1+1+0 = 4
S(1,0) = s(0,0) - s(1,0) + s(0,1) - s(1,1) = 2 -1+1 -0 = 2
S(0,1) = s(0,0) + s(1,0) - s(0,1) - s(1,1) = 2+1 -1 -0 = 2
S(1,1) = s(0,0) - s(1,0) - s(0,1) + s(1,1) = 2 -1 -1+0 = 0
После аналогичного вычисления H(k,l) и перемножения S(k,l)= S(k,l) H(k,l):
S(k,l) =  , H(k,l)=
, H(k,l)= 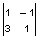 , Z(k,l)=
, Z(k,l)= 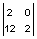 .
.
После обратного ДПФ размера 2 х 2 получим результат циклической свертки: z(n,m) = 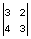
Дополним опорные области s(.) и h(.) до размера 4 х 4 (для исключения искажения спектра, в принципе,
достаточен размер 3 х 3), и повторим вычисления:
s(n,m)=  , h(n,m)=
, h(n,m)=  .
.
S(k,l)= 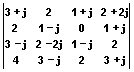 , H(k,l)=
, H(k,l)=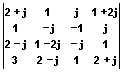 .
.
S(k,l)= 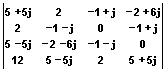 . s(n,m)=
. s(n,m)=  .
.
Сравнение данного результата с ДПФ размером 2 х 2 позволяет наглядно видеть эффект
цикличности свертки.
В настоящее время имеются разнообразные и весьма эффективные алгоритмы ДПФ. Для прямого вычисления P-мерного ДПФ требуется (N
1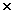 N2
N2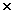 ...
...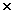 NP)2 операций умножения и сложения. Для многомерного ДПФ, как и для одномерного, существуют алгоритмы быстрых преобразований Фурье. Простейший из них в двумерном ДПФ - разбиение на строки и столбцы, который мы уже рассматривали. Аналогично, Р-мерное ДПФ может заменяться Р-операциями одномерных ДПФ, при этом общее количество операций умножения и сложения сокращается.
NP)2 операций умножения и сложения. Для многомерного ДПФ, как и для одномерного, существуют алгоритмы быстрых преобразований Фурье. Простейший из них в двумерном ДПФ - разбиение на строки и столбцы, который мы уже рассматривали. Аналогично, Р-мерное ДПФ может заменяться Р-операциями одномерных ДПФ, при этом общее количество операций умножения и сложения сокращается.
литература
9. Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов. – М.: Мир, 1988. – 488 с.
Copyright ©2005 Davydov А.V.
|
|
