ПРЕОБРАЗОВАНИЕ ХАРТЛИ
Ни одна вещь не возникает беспричинно, но все возникают на каком-нибудь основании и в силу необходимости.
Демокрит. Древнегреческий философ, атомистик, V-IV в. до н.э.
Содержание
Введение.
1. Основные сведения
. Определение преобразования. Связь преобразований Фурье и Хартли. Энергетический и фазовый спектры.2. Свойства преобразования.
Линейность. Четность и нечетность спектральных функций. Измерение аргумента функции. Теорема запаздывания. Преобразование производной. Преобразование интеграла. Преобразование свертки и произведения. Преобразование функции корреляции. Двумерное преобразование Хартли.3. Дискретное преобразование Хартли
. Формулы преобразования. Спектры числовых рядов. Свойства дискретного преобразования. Цифровая фильтрация методом свертки. Двумерная дискретная фильтрация.Литература.
ВВЕДЕНИЕ
Преобразование Хартли является аналогом преобразования Фурье и может применяться для спектрального анализа, фильтрации и обработки сигналов. Название преобразование получило по имени Р.Хартли, опубликовавшего в 1942 г. статью о паре интегральных преобразований - прямом и обратном, использующих введенную им функцию cas
q = cos q + sin q . Преобразование оставались в забвении до 80-х годов прошлого века.Обращение к преобразованию Хартли было обусловлено ситуацией, сложившейся в ряде методов обработки информации, использующих вещественные последовательности данных (одномерных, двумерных, трехмерных), обработку которых желательно осуществлять в области вещественных чисел с помощью взаимно симметричных прямого и обратного преобразований. В отличие от преобразования Фурье, отображающего вещественные функции в комплексную область и несимметричного по комплексной переменной (изменение знака при переходе от прямого к обратному преобразованию), преобразование Хартли осуществляет преобразования только в вещественной области, отображая вещественные сигналы s(t) в вещественные S(
w), прямое и обратное преобразование Хартли полностью взаимно симметричны. Большой вклад в развитие преобразования внес Р. Брейсуэлл, разработавший основы теории непрерывного и дискретного преобразования Хартли, а также один из вариантов его быстрого преобразования. Применение преобразования перспективно для обработки изображений.10.1. Основные сведения
Определение преобразования.
Преобразование Хартли задается парой формул:Sh(w) = (1/
)
s(t) cas wt dt (10.1.1)
s(t) = (1/)Sh(w) cas wt dw (10.1.2)
где функция cas представляет собой сумму косинуса и синуса одного аргумента:
cas wt = cos wt + sin wt. (10.1.3)
Множители 1/обусловлены применением в формулах аргумента
Sh(f) =s(t) cas 2pft dt (10.1.1')
s(t) =Sh(f) cas 2pft df (10.1.2')
На первый взгляд в формулах отсутствуют существенные отличия от интегральных преобразований Фурье, однако на практике эти различия могут быть достаточно ощутимыми, что определяется вещественным характером функции Sh(f).
Связь преобразований Фурье и Хартли
хорошо просматривается при анализе свойств симметрии преобразований.Допустим, имеется произвольная функция s(t)
S(f), где Sh(f) и S(f) – результаты преобразования Хартли и Фурье, Хартли- и Фурье-образы функции s(t) соответственно. Любая функция y(x) может быть представлена в виде суммы четной и нечетной компонент, и однозначно по ним восстановлена. Четная компонента определяется как полусумма функции y(x) и ее зеркального изображения y(-x), нечетная компонента определяется как полуразность этих функций и обладает свойством антисимметрии, т.е. y(-x) = -y(x). Запишем для преобразования Хартли:
Sh(f) =s(t) cas 2pft dt =s(t) cos 2pft dt + s(t) sin 2pft dt.
Sh(f) = Shsym(f) + Shasym(f),
Shsym(f) = [Sh(f)+Sh(-f)]/2 = s(t) cos 2pft dt, (10.1.4)
Shasym(f) = [Sh(f) - Sh(-f)]/2 = s(t) sin 2pft dt, (10.1.5)
где Sh
sym(f) и Shasym(f) – четная и нечетная компоненты Sh(f).C другой стороны, для преобразования Фурье имеем:
S(f) =s(t) exp(-2pft) dt = A(f) – j B(f).
A(f) =s(t) cos 2pft dt, - четная вещественная часть спектра,
B(f) =s(t) sin 2pft dt, - нечетная мнимая часть спектра.
Сравнивая эти две группы выражений, нетрудно сделать выводы по формулам связи преобразований Фурье и Хартли:
S(f) = Shsym(f) – j Shasym(f), (10.1.5)
Sh(f) = A(f) - B(f). (10.1.7)
Таким образом, преобразование Фурье равно разности четной составляющей преобразования Хартли и нечетной составляющей, умноженной на j, а преобразование Хартли определяется как разность вещественной и мнимой составляющих преобразования Фурье.
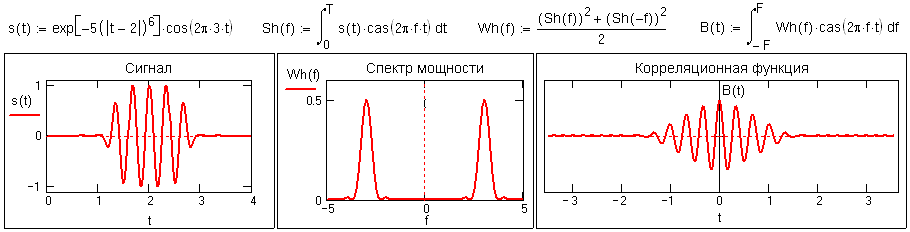
Пример прямого и обратного преобразования Хартли для простого сигнала (гауссиан с быстро затухающей частотной характеристикой) и сопоставления четной и нечетной частей его спектра с действительной и мнимой частью спектра Фурье приведен на рис. 10.1.1.
Как можно видеть на рисунке, спектр Хартли Sh(f) даже такого простого сигнала, как гауссиан, выглядит достаточно сложно, равно как и его четная и нечетная составляющие, и мало пригоден для визуального анализа. Отметим, однако, что действительная и мнимая части преобразования Фурье, хотя и имеют определенный физический смысл, как амплитудные распределения косинусных и синусных колебаний, в качественном анализе сигналов также используются достаточно редко. Гораздо большее практическое значение для анализа имеют модуль и фаза спектра (амплитудно-частотная и фазочастотная характеристика) и спектр плотности мощности сигнала. Отметим также, что для преобразования Хартли не характерна избыточность преобразования Фурье, т.к. в общем случае вещественные функции Хартли эквивалентны сопряженным комплексным функциям Фурье.
Рис. 10.1.1.
Энергетический и фазовый спектры.
Как известно, энергетический спектр преобразования Фурье (спектр плотности мощности сигнала) задается выражением:W(f) = A2(f) + B2(f).
Частотный спектр плотности мощности сигнала не должен зависеть от формы математического представления спектра. Из этих соображений для вычисления энергетического спектра по спектру Хартли следует:
Wh(f) = (Shsym(f))2 + (Shasym(f))2 = [Sh(f)+Sh(-f)]2/4 +[Sh(f) - Sh(-f)]2/4,
Wh(f) = [Sh2(f)+Sh2(-f)]/2. (10.1.8)
Аналогично, вычисление фазовой частотной характеристики сигнала:
j
(f) = argtg(B(f)/A(f)) = argtg(-Shasym(f)/ Shsym(f)),j
(f) = argtg(-[Sh(f) - Sh(-f)] / [Sh(f)+Sh(-f)]). (10.1.9)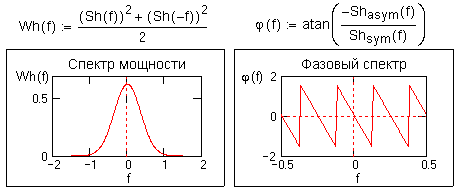
На рис. 10.1.2. приведено продолжение вычислений для сигнала на рис. 10.1.1 и показаны частотные функции спектра плотности мощности и фазовой характеристики сигнала.
С учетом всех вышеприведенных выражений преобразование Хартли может рассматриваться как гладкая форма представления вещественного сигнала. Будучи чисто вещественным, преобразование Хартли не требует других способов представления, тогда как другие способы могут быть непосредственно получены из него.
10.2. свойства преобразования
Линейность.
Преобразование Фурье относится к числу линейных интегральных операций, т.е. спектр суммы сигналов равен сумме спектров этих сигналов.
ansn(t) anShn(w). (10.2.1)
Пример суммирования сигналов и его отображения в суммирования спектров приведен на рис. 10.2.1:
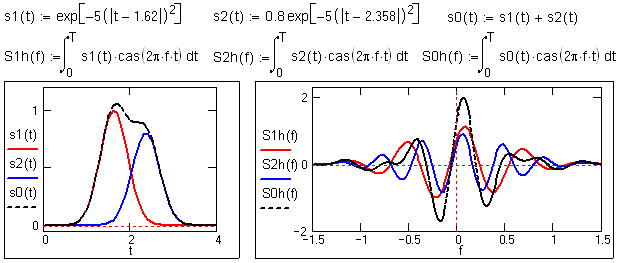
Рис. 10.2.1. Сигналы и их спектры. s0(t)=s1(t)+s2(t)
Ы S1h(f)+S2h(f) = S0h(f).Четность и нечетность спектральных функций.
Свойства четности преобразования Фурье распространяются и на преобразование Хартли. Для четных сигналов равен нулю интеграл (10.1.5) и в спектре Хартли отсутствует нечетная составляющая (функция Sh(f) – четная). Соответственно, для нечетных сигналов равен нулю интеграл (10.1.4) и спектральная функция нечетная. Это можно наглядно видеть на рис. 10.2.2.
Рис. 10.2.2. Преобразование Хартли четных и нечетных функций.
Энергетические и фазовые частотные спектры, как и для преобразования Фурье, также являются четными и нечетными соответственно.
Изменение аргумента функции
(сжатие или расширение сигнала) приводит к обратному изменению аргумента ее хартли-образа и обратно пропорциональному изменению его модуля (рис. 10.2.3). Действительно, если s(t)Sh(f), то при изменении длительности сигнала с сохранением его формы (растяжении сигнала по временной оси), т.е. для сигнала с новым аргументом s(x) = s(at) при x=at, получаем:
s(at) s(at) cas(2pft) dt = (1/a)s(x) cas(2pfx/a) dx
s(at) (1/a) Sh(f/a). (10.2.2')
Выражение (10.2.2') действительно при а>0. При а<0 происходит зеркальный поворот сигнала относительно вертикальной оси, а замена переменной t=x/a вызывает перестановку пределов интегрирования и, соответственно, изменение знака спектра:
s(at) -(1/a) Sh(f/a). (10.2.2'')
Обобщенная формула изменения аргумента:
s(at) (1/|a|) Sh(f/a), a ≠ 0 (10.2.2)
Если под аргументом функции и ее спектра понимать определенные физические единицы, например, время - частота, то отсюда следует: чем короче по своей длительности сигнал, тем шире по частоте его спектр, и наоборот, что полностью аналогично преобразованию Фурье.
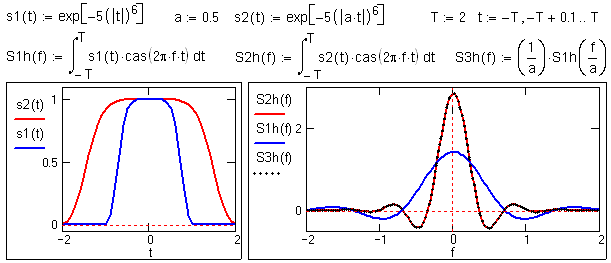
Рис. 10.2.3.
Теорема запаздывания.
Применяя замену переменной t-to = x, после соответствующих тригонометрических преобразований (выполнить самостоятельно) получаем (рис. 10.2.4):s(t-to)s(t-to) cas(2pft) dt = cos(2pfto) Sh(f) + sin(2pfto) Sh(-f). (10.2.3)
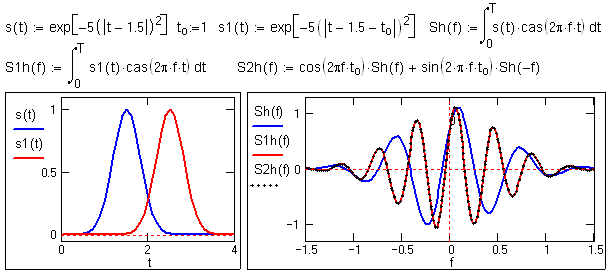
Рис. 10.2.4. Изменение спектра сигнала при сдвиге.
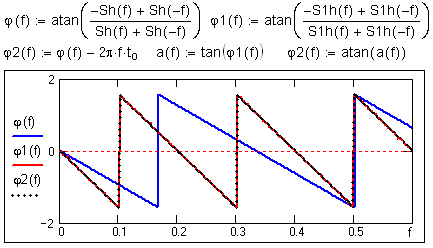
Совершенно очевидно, что амплитуды гармоник сигнала (модуль спектра) при его сдвиге изменяться не должны. Запаздывание (сдвиг, смещение) сигнала по аргументу функции на интервал t
o, как и для преобразования Фурье, приводит к изменению фазочастотной функции спектра (фазового угла всех гармоник) на величину -2pfto. Если известна фазовая характеристика j(f) спектра исходного сигнала, то для определения фазовой функции сдвинутого сигнала достаточно выполнить вычисление j(f, to) = j(f) – 2pfto (рис. 10.2.5).Преобразование производной
(дифференцирование сигнала):s'(t) = d[s(t)]/dt = d[Sh(f) cas(2pft) df]/dt =Sh(f) [d(cas(2pft))/dt] df =
= - 2pf Sh(-f) cas(2pft) df -2pf Sh(-f). (10.2.4)
Таким образом, дифференцирование сигнала отображается в спектральной области простым умножением зеркального изображения спектра сигнала на оператор дифференцирования сигнала в частотной области
-2pf. Умножение на 2pf приводит к обогащению спектра производной сигнала высокочастотными составляющими (по сравнению с исходным сигналом) и уничтожает составляющие с нулевой частотой.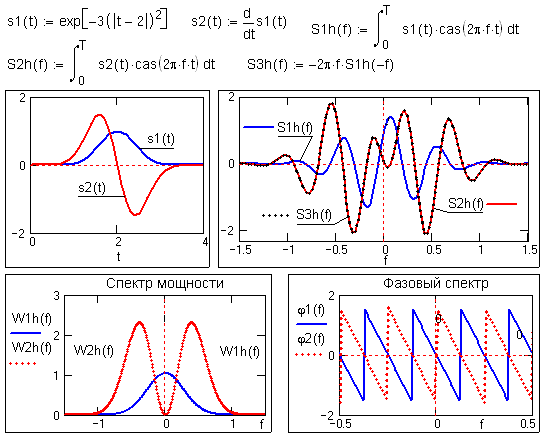
Пример сигнала, его производной и соответствующих им спектров приведен на рис. 10.2.6. По изменению аргумента спектра можно видеть, что для всех гармоник спектра появляется сдвиг фаз на
p/2 (900) для положительных частот, и на -p/2 (-900) для отрицательных частот.Аналогично могут быть получены выражения для производных более высокого порядка. В частности, для второй производной:
d2[s(t)]/dt2 = -(2pf)2 Sh(f).
Преобразование интеграла сигнала в частотной области при известном спектре сигнала может быть получено из следующих соображений. Если имеет место y(t) = d[s(t)]/dt -2pf Sh(-f) = Yh(f), то должна выполняться и обратная операция:
s(t) =
y(t)dt 
(1/2pf) Yh(-f). (10.2.5)
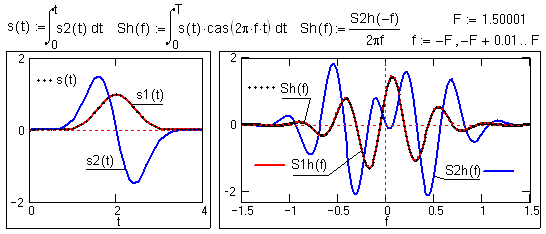
На рис. 10.2.7 выполнено интегрирование сигнала s2(t) = d[s(t)]/dt, дифференцирование которого показано на рис. 10.2.6, т.е. восстановление сигнала s(t). Как и в преобразовании Фурье, оператор интегрирования (1/2
pf) в частотной области f>1 ослабляет гармоники высоких частот, а при f<1 усиливает низкие частоты. Фазовый спектр сигнала смещается на -900 для положительных частот и на 900 для отрицательных. При f=0 в выражении (10.2.5) имеется особая точка (деление на ноль), вычисление значения в которой должно выполняться путем предельного перехода (f® 0).Преобразование свертки и произведения
сигналов у Хартли в общем случае выглядит сложнее, чем в преобразовании Фурье. Для свертки сигналов имеем:s(t) * u(t) 0.5 [Sh(f)Uh(f) - Sh(-f)Uh(-f) + Sh(f)Uh(-f) + Sh(-f)Uh(f)]. (10.2.6)
Для произведения сигналов:
s(t) u(t) 0.5 [Sh(f)*Uh(f) - Sh(-f)*Uh(-f) + Sh(f)*Uh(-f) + Sh(-f)*Uh(f)]. (10.2.7)
Однако это не более чем видимость, т.к. выполняя свертку через преобразование Фурье s(t)
*u(t)S(f)U(f) мы производим перемножение двух комплексных функций A(f)-jB(f) с соответствующим суммированием также произведений четырех членов.
С позиций обработки и фильтрации данных, существенное значение имеет тот фактор, что если хотя бы одна из функций, входящих в формулу свертки, является либо четной, либо нечетной, то формулы прямых преобразований Хартли и Фурье для свертки полностью совпадают. Как правило, операторы фильтров для исключения сдвига фазы обрабатываемых данных выполняют симметричными
, при этом преобразование Хартли имеет вид:h(t) * s(t) Hh(f) Sh(f). (10.2.6')
Если оператор фильтра асимметричный (нечетный), то формула приобретает вид:
h(t) * s(t) Hh(f) Sh(-f). (10.2.6'')
Преобразование функции корреляции.
В частотной области преобразование Хартли автокорреляционной функции, как и преобразование Фурье, представляет собой спектральную плотность мощности сигнала:Bs(t) = б s(t), s(t+t)с 0.5 [Sh2(f) + Sh2(-f)] = Whs(f). (10.2.8)
Учитывая четность автокорреляционной функции и спектра мощности, оно практически ничем не отличается от преобразования Фурье, за исключением алгоритма вычислений. На рис. 10.2.8 приведен пример вычисления автокорреляционной функции сигнала с использованием преобразования Хартли.
Двумерное преобразование Хартли. Для двумерной функции s(x, y) двумерное преобразование Хартли задается выражениями:
Sh(u, v) =s(x, y) cas[2p(ux+vy)] dxdy, (10.2.9)
s(x, y) =Sh(u, v) cas[2p(ux+vy)] dudv, (10.2.10)
Связь двумерного преобразования Хартли с преобразованием Фурье легко устанавливается аналогично одномерному преобразованию:
Sh(u, v) = Re(S(u, v)) – Im(S(u, v)). (10.2.11)
Соответственно, для двумерного ПХ сохраняются свойства четности и нечетности одномерного преобразования. Если функция s(x, y) обладает свойством круговой симметрии, то ее двумерное преобразование Хартли совпадает с двумерным преобразованием Фурье.
Основные свойства двумерного преобразования:
Подобие:
s(ax, by) (1/|ab|) Sh(u/a, v/b). (10.2.12)
Сдвиг:
s(x-a, y-b) cos(2p(au+bv)) Sh(u, v)+sin(2p(au+bv)) Sh(-u, -v). (10.2.13)
Модуляция:
s(x, y) cos(2p(uox+voy)) 0.5 [Sh(u-uo, v-vo) + Sh(u+uo, v+vo)]. (10.2.14)
Корреляция:
B(tx, ty) T [Sh2(u, v) + Sh2(-u, -v)]. (10.2.15)
Произведение при разделении переменных:
s(x) h(x) 0.5 [Sh(u, v)Hh(u, v) - Sh(-u, -v)Hh(-u, -v) +
+ Sh(u, v)Hh(-u, -v)+ Sh(-u, -v)Hh(u, v)]. (10.2.16)
Свертка:
s(x, y)*h(x, y) 0.5T [Sh(u, v)Hh(u, v) - Sh(-u, -v)Hh(-u, -v) +
+ Sh(u, v)Hh(-u, -v)+ Sh(-u, -v)Hh(u, v)]. (10.2.17)
10.3. дискретное преобразование хартли
Формулы преобразования.
Как обычно, для представления функций с равномерной дискретизацией примем обозначение s(nDt). Количество отсчетов функции равно N, интервал задания [0, N-1]. При Dt = 1 альтернативное обозначение функций s(n) є sn. Прямое и обратное преобразование Хартли (ДПХ) в общей форме:Sh(mDf) = (1/N)
s(nDt) cas(2p mDf nDt), n = 0…N-1, (10.3.1)
s(nDt) =
Sh(mDt) cas(2p mDf nDt), m = 0…M-1. (10.3.2)
Здесь: М – количество отсчетов спектральной функции с шагом дискретизации по частоте
Df. Как и в преобразовании Фурье, дискретизация сигнала вызывает периодизацию частотных функций с аналогичными нормами корректности преобразования. Частота Найквиста для главного частотного диапазона fN = 1/2Dt, главный частотный диапазон вычислений от 0 до 2fN (при Dt=1 от 0 до 1), оптимальный и достаточный шаг частотной дискретизации для сохранения всей сигнальной информации и восстановления сигнала при обратном преобразовании без погрешности Df = 1/N. Пример преобразования приведен на рис. 10.3.1.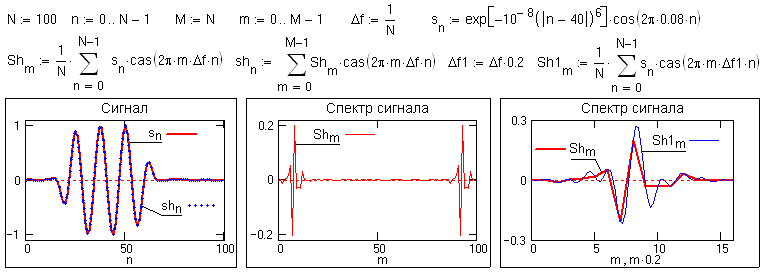
Спектры числовых рядов. При обработке произвольных рядов данных значение Dt по умолчанию принимается равным 1 и формулы (10.3.1-10.3.2) применяются в следующем виде:
Sh(m) = (1/N)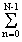s(n) cas(2p m n/N), (10.3.1')
s(n) =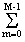Sh(m) cas(2p m n/N). (10.3.2')
Спектр сигналов является непрерывной функцией. Оптимальная дискретизация спектра при малом количестве данных может существенно искажать форму спектра, и для визуального просмотра шаг дискретизации может быть уменьшен, как это показано на рис. 10.3.1 для спектра Sh1. Однако при этом следует учитывать, что при уменьшении шага спектра в k-раз для восстановления сигнала из спектра требуется выполнять расчет с увеличением в k раз количества точек спектра М.
Это объясняется тем, что спектр Хартли в главном диапазоне не имеет избыточности, как это характерно для преобразования Фурье (комплексная сопряженность). В диапазоне главного периода [-M/2, M/2], спектр Хартли в общем случае представляет собой произвольную функцию (рис. 10.3.2). При смещении расчетного диапазона спектра в интервал [0, M-1], что выполняется для ускорения расчетов и исключения отрицательного индексирования отсчетов, восстановление сигнала по интервалу [0, M/2] невозможно, за исключением четных и нечетных функций, где информационная избыточность заложена в задании самой функции.
Свойства дискретного преобразования по своей сущности аналогичны свойствам непрерывного преобразования. С учетом смещения расчетного главного диапазона спектра в область положительных индексов на половину периода, значениям Sh(-m) соответствуют значения Sh(M-m) и, соответственно, несколько изменяются формулы свойств преобразования. Из чисто практических соображений построения алгоритмов расчетов заметим, что при m=0 значениям Sh(M-m) должно соответствовать значение Sh(0). Для сохранения общности алгоритмов это выполняется расчетом спектров в формулах (10.3.1) не до индекса M-1 (при M=N), а до индекса М (с сохранением предела суммирования М-1 в формулах обратного преобразования).
Вычисление четной и нечетной составляющих:
Shsym(m) = [Sh(m)+Sh(M-m)]/2, (10.3.3)
Shasym(m) = [Sh(m) - Sh(M-m)]/2. (10.3.4)
Связь с преобразованием Фурье:
S(m) = Shsym(m) – j Shasym(M-m), (10.3.5)
Энергетический и фазовый спектры:
Wh(m) = [Sh2(m)+Sh2(M-n)]/2. (10.3.6)
j
(m) = argtg(-[Sh(m) - Sh(M-n)] / [Sh(m)+Sh(M-n)]). (10.3.7)Сдвиг сигнала. Смещение на полпериода нумерации отсчетов вызывает изменение знака синусного члена [32]:
s(n-no) = cos(2pmno/N) Sh(m) - sin(2p mno/N) Sh(M-m). (10.3.8)
Преобразование производной:
s'(n) = (2pm/N) Sh(M-m). (10.3.9)
Функция корреляции:
Bs(k) = б s(n), s(n+k)с 0.5 [Sh2(m) + Sh2(M-m)] = Whs(m). (10.3.10)
Преобразование свертки:
s(n)*u(n) 0.5N[Sh(m)Uh(m)-Sh(M-m)Uh(M-m)+Sh(m)Uh(M-m)+Sh(M-m)Uh(m)]. (10.3.11)
Цифровая фильтрация методом свертки. Выполнение свертки через преобразование Хартли полностью аналогично циклической свертке через преобразование Фурье:
s(n) = x(n)*y(n) Xh(n)Yh(n) = Sh(n) s(n). (10.3.12)
Как и для ДПФ, при фильтрации сигналов с выполнением свертки через частотную область ДПХ для исключения наложений от боковых периодов на сигнал главного периода интервал задания сигнала следует продлевать (нулями, значениями фона или тренда) на длину оператора фильтра, для симметричных операторов – с обеих сторон интервала. После выполнения этой операции длина самого оператора фильтра, которая обычно много меньше длины сигнала, также должна продлеваться до количества задания отсчетов сигнала с учетом его продления, т.к. умножение спектров сигнала и фильтра требует равного количества отсчетов их спектрального представления.
Двумерная дискретная фильтрация. Спектр Хартли функции s(k, n), представленной в виде матрицы размера К x N (k=kDx, n=nDy), имеет вид вещественной матрицы Sh(m, p) также размером K x N, при этом прямые и обратные преобразования матриц записываются в виде:
Sh(m, p) = (1/KN)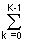
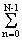s(k, n) cas(2pkn/K+2pkn/N), (10.3.13)
s(k, n) = (1/KN)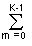
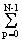Sh(m, h) cas(2pkn/K+2pkn/N). (10.3.14)
литература
32. Брейсуэлл Р. Преобразование Хартли. Теория и приложения. – М.: Мир, 1990.
Дополнительная.
1. Злобин С.Л, Стальной А.Я. "Двумерное быстрое преобразование Хартли в цифровой обработке изображений". Доклады 6–ой Международной конференции "Цифровая обработка сигналов и её применение". Том 2, стр. 114–116. Труды РНТОРЭС им. А.С. Попова. Москва, Россия, 2004 г.
2. Кантор И. Эффективное вычисление дискретного преобразования Фурье и дискретного преобразования Хартли. – 2002.
http://algolist.manual.ru/maths/fft_art.zip.
Copyright ©2007 Davydov А.V.
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|
 |