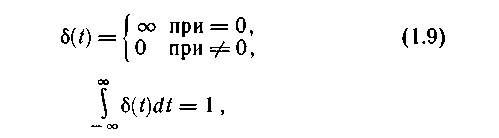
где д(t) - дельта-функция, отличная от нуля в начале координат (при
t = 0).Для более общего случая, когда дельта-функция отличается от нуля в момент времени
t=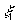
(рис.1.3), имеем
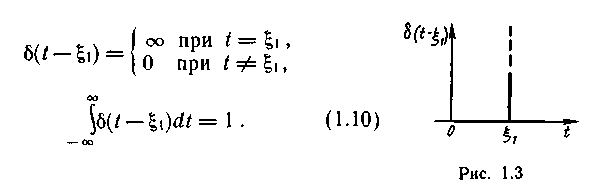
Такая математическая модель соответствует абстрактному импульсу бесконечно малой длительности и безграничной величины. Единственным параметром, правильно отражающим реальный сигнал, является время его действия. Однако, учитывая (1.10), с помощью дельта-функции можно выразить значение реального сигнала
u(t) в конкретный момент времени ой: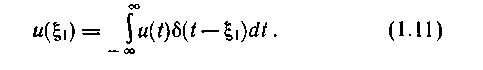
Равенство (1.11) справедливо для любого текущего момента времени
t. Заменив ой на t и приняв в качестве переменной интегрирования о, получим
Таким образом, функция
u(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Ортогональность совокупности таких импульсов очевидна, так как они не перекрываются во времени.Разложение (1.12) имеет большое значение в теории линейных систем, поскольку, установив реакцию системы на элементарный входной сигнал в виде дельта-функции (импульсную переходную функцию), можно легко определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с "площадями", равными соответствующим значениям входного сигнала.
С помощью дельта-функций можно также представить периодическую последовательность идеализированных импульсов с постоянными или меняющимися уровнями. Обозначив через
u
(t) функцию, равную u(k
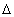t) в точках t = k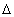t и нулю в остальных точках, запишем:
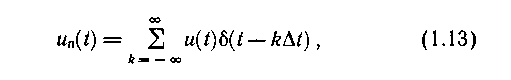
где Дt - период следования импульсов.
Поскольку умножение
u(t) на дельта - функцию в момент времени t = k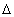t соответствует получению отсчета этой функции, uп(k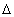t) может представлять результат равномерной дискретизации функции u(t).
(Фотометрический парадокс, парадокс Ольберса - это один из парадоксов космологии, заключающийся в том, что во Вселенной, равномерно заполненной звёздами, яркость неба (в том числе ночного) должна быть примерно равна яркости солнечного диска. Это должно иметь место потому, что по любому направлению неба луч зрения рано или поздно упрется в поверхность звезды.
Иными словами парадос Ольберса заключается в том, что если Вселенная бесконечна, то черного неба мы не увидим, так как излучение дальних звезд будет суммироваться с излучением ближних, и небо должно иметь среднюю температуру фотосфер звезд. При поглощении света межзвездным веществом, оно будет разогреваться до температуры звездных фотосфер и излучать также ярко, как звезды. Однако в дело вступает явление "усталости света", открытое Эдвином Хабблом, который показал, что чем дальше от нас расположена галактика, тем больше становится красным свет ее излучения, то есть фотоны как бы "устают", отдают свою энергию межзвездной среде. На очень больших расстояниях галактики видны только в радиодиапазоне, так как их свет вовсе потерял энергию идя через бескрайние просторы Вселенной. Подробнее читайте в FAQ по эфирной физике.
|
|
 |