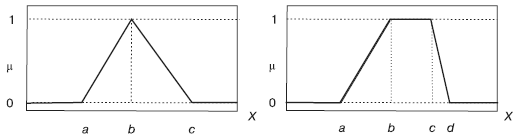
Рис. 15. Типовые функции принадлежности
Хороший пример обогащения одной технологии (хранилища данных) другой (нечеткая логика) демонстрируют нечеткие срезы (fuzzy slices). Под ними понимаются фильтры по измерениям, в которых фигурируют нечеткие величины, например «все молодые заемщики с небольшим доходом». В реляционных базах данных эту роль выполняют нечеткие запросы (fuzzy queries, flexible queries), которые впервые предложены в начале 80-х гг. в работах Д. Дюбуа и Г. Прада.
Так как информация в ХД присутствует в четком виде, для использования в фильтрах нечетких понятий нужно предварительно формализовать их, что делается при помощи нечетких множеств, описание которых приводится ниже.
Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Данные понятия были впервые предложены американским ученым Лотфи Заде (Lotfi Zadeh) в 1965 г. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.
Характеристикой нечеткого множества выступает функция принадлежности (membership function). Обозначим через μ(x) степень принадлежности элемента x к нечеткому множеству, представляющую собой обобщение понятия характеристической функции обычного множества. Тогда нечетким множеством С называется множество упорядоченных пар вида C = {μ(x)/x}, при этом μ(x) может принимать любые значения в интервале [0, 1], x ∈ X. Значение μ(x) = 0 означает отсутствие принадлежности к множеству, 1 — полную принадлежность.
Проиллюстрируем это на простом примере. Формализуем неточное определение «неблагонадежный заемщик». В качестве X (область рассуждений) будет выступать количество случаев просроченной задолженности по кредиту за последние 6 месяцев. Пусть оно изменяется от 0 до 6. Нечеткое множество, определенное экспертом, может выглядеть следующим образом:
C = {0/0; 0,4/1; 0,7/2; 0,9/3; 1/4; 1/5; 1/6}.
Так, заемщик, совершивший две просрочки, принадлежит к множеству «неблагонадежный» со степенью принадлежности 0,7. Для одного банка такое число просрочек может быть крайне существенным, для другого — просто тревожным сигналом. Именно в этом и проявляется нечеткость задания соответствующего множества.
Для переменных, относящихся к непрерывному виду данных, функцию принадлежности удобнее задать аналитической формулой и для наглядности изобразить графически. Существует свыше десятка типовых форм кривых для задания функций принадлежности. Рассмотрим самые популярные кусочно-линейные: треугольную и трапецеидальную (рис. 15).

Рис. 15. Типовые функции принадлежности
Треугольная функция принадлежности определяется тройкой чисел (a, b, c), и ее значение в точке x вычисляется согласно выражению:

Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (a, b, c, d):
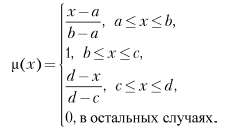
Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми необходимыми для расчетов являются пересечение, объединение и отрицание.
μ(x) = min(μA(x), μB(x)).
μ(x) = max(μA(x), μB(x)).
μ(x) = 1 − μA(x),
где μ(x) — результат операции;
μA(x) — степень принадлежности элемента x к множеству А;
μB(x) — степень принадлежности элемента x к множеству B.
Совокупность нечетких множеств, относящихся к одному объекту, образует лингвистическую переменную. Например, лингвистическая переменная Возраст может принимать значения Молодой, Средний, Пожилой (их еще называют базовым терм-множеством, или термами). Зададим область рассуждений в виде X = {x | 0 < x < 90} (годы). Теперь осталось построить функции принадлежности для каждого терма (рис. 16).
Каждая функция принадлежности описывается четверкой чисел: Молодой = {0; 0; 12; 40}, Средний = {20; 30; 50; 70}, Преклонный = {50; 60; 90; 90}.

Рис. 16. Графическое изображение лингвистической переменной «Возраст»
Лингвистические переменные можно задать для любого измерения, атрибута измерения или факта, значения которого имеют непрерывный вид. Их параметры: названия, терм-множества, параметры функций принадлежности — будут содержаться в семантическом слое хранилища данных (рис. 17).
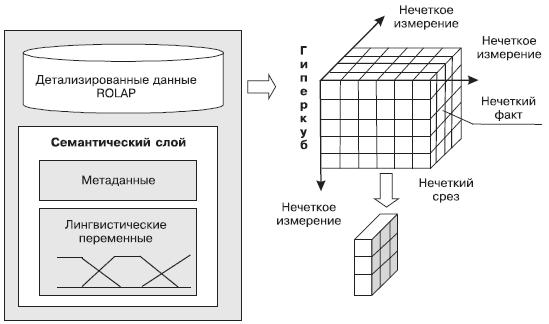
Рис. 17. Вариант организации хранилища данных с поддержкой нечетких срезов
Результатом выполнения нечеткого среза, помимо самого подмножества ячеек гиперкуба, удовлетворяющих заданным условиям, является индекс соответствия срезу CI ∈ [0, 1]. Он представляет собой итоговую степень принадлежности к нечетким множествам измерений и фактов, участвующих в сечении куба, и рассчитывается для каждой записи набора данных. Чтобы ускорить выполнение запросов к ХД, часто задают верхнюю границу индекса соответствия CI > а. Это позволяет уже на уровне SQL-запроса отсеять записи, которые заведомо не будут удовлетворять минимальному порогу индекса соответствия (рис. 18). На рисунке видно, что элементы нечеткого множества со значениями в интервале [xf, x2] обеспечат степень принадлежности не ниже а.
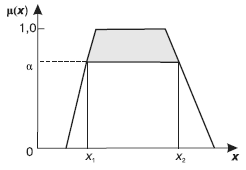
Рис. 18. Нечеткое множество
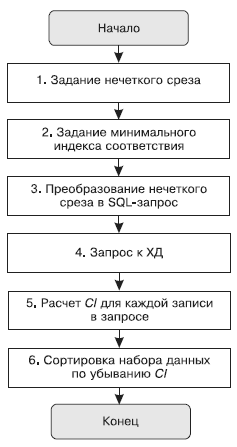
Рис. 19. Алгоритм получения нечеткого среза
Алгоритм формирования нечеткого среза иллюстрирует схема (рис. 19). На шаге 1 используется семантический слой хранилища данных. На шаге 3 в результирующий SQL-запрос попадают границы с учетом минимального индекса соответствия а. Шаг 5 предполагает применение нечетких логических операций.
Рассмотрим пример. Пусть в хранилище содержится информация о соискателях вакансий, и срез (четкий) по измерениям Код анкеты, Возраст и Стаж работы обеспечивает следующий набор данных (табл. 4).
Очевидно, что Код анкеты — это служебное поле. Для возраста будем использовать лингвистическую переменную, определенную на рис. 16, а для поля Стаж работы — переменную, определенную на рис. 20. Каждая функция принадлежности описывается числами: Малый = {0; 0; 6}, Продолжительный = {3; 6; 10; 20}, Большой = {15; 25; 40; 40}.
Таблица 4. Срез по измерениям «Возраст» и «Стаж работы»
|
Код анкеты |
Возраст |
Стаж работы |
|
1 |
23 |
4 |
|
2 |
34 |
11 |
|
3 |
31 |
10 |
|
4 |
54 |
36 |
|
5 |
46 |
26 |
|
6 |
38 |
15 |
|
7 |
21 |
1 |
|
8 |
23 |
2 |
|
9 |
30 |
8 |
|
10 |
30 |
12 |

Рис. 20. Графическое изображение лингвистической переменной «Стаж работы»
Сделаем нечеткий срез «Возраст = Средний и Стаж работы = Продолжительный». Например, для анкеты 4 получим:

Аналогично рассчитаем степени принадлежности к итоговому нечеткому множеству для каждого претендента, зададим минимальный индекс соответствия, равный 0,3, и получим результат, показанный в табл. 5.
Таблица 5. Результат нечеткого среза
|
Код анкеты |
Возраст |
Стаж работы |
Индекс соответствия |
|
3 |
31 |
10 |
1 |
|
9 |
30 |
8 |
1 |
|
6 |
38 |
15 |
1 |
|
2 |
34 |
11 |
0,9 |
|
10 |
30 |
12 |
0,8 |
|
8 |
23 |
2 |
0,3 |
|
1 |
23 |
4 |
0,3 |
Нечеткий поиск в хранилищах данных принесет аналитику максимальную пользу в случаях, когда требуется не только извлечь информацию, оперируя нечеткими понятиями, но и каким-то образом проранжировать ее по убыванию (возрастанию) степени релевантности запроса. Это позволит ответить на следующие вопросы: каких клиентов обзвонить в первую очередь, кому сделать рекламное предложение и т.д.
|
|