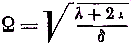члены в случае колебаний продольных должны исчезнуть из уравнений, и мы получаем первую группу:
УМОВ Николай Алексеевич
ЗАКОНЫ КОЛЕБАНИИ В НЕОГРАНИЧЕННОЙ СРЕДЕ ПОСТОЯННОЙ УПРУГОСТИ
Впервые напечатано в Математическом сборнике, т. 5, 1870 г. (Прим. ред.)
III.
КОЛЕБАНИЯ ПРОДОЛЬНЫЕ§ 13. Обращаясь к основным дифференциальным уравнениям колебаний в § 7, мы заметим, что когда
умножим их на — = к,
2, они будут содержать члены, из которых одни имеют коэффициентом квадрат скорости и поперечных колебаний, другие-квадрат скорости продольных колебаний.Первые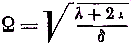члены в случае колебаний продольных должны исчезнуть из уравнений, и мы получаем первую группу:
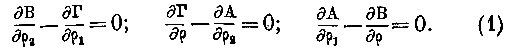
Так как поверхность
p по нашему выбору есть поверхность волны, то в уравнениях § 7 мы должны удержать одно колебание R и приравнять нулю колебания /?! и R.2, совершающиеся в плоскости, касательной к волне. Вследствие этого находим, полагая //=1: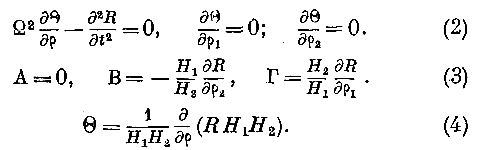
Так как А = 0, то уравнения (1) примут вид:
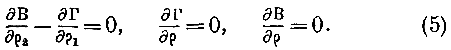
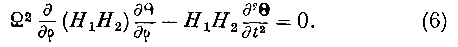
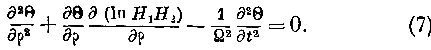
Умножая первое из уравнений (2) на
//i//2, дифференцируя по p и обращая внимание на уравнение (4), находим:Но но уравнениям (2) В не зависит ни от рх, ни от [-,. Следовательно, означая через
&F частную производную от функции F по одной из переменных ^, р.2, мы получаем пз уравнения (7):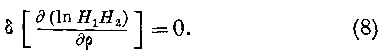
Подставляя в ото выражение величавы
II lt Н2, найденные в § 3, приравнивая нулю коэффициенты при различных степенях ,., мы находим следующие условия, которым должна удовлетворять волновая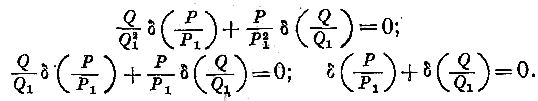
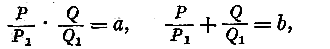
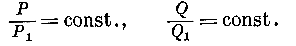
Но мы знаем, что подобные соотношения имеют место только для сферы, круглого цилиндра и плоскости. Отсюда заключаем, что
одни изотермические волновые поверхности могут распространять колебания продольные.
Итак, если поверхность сотрясения или начальная волна не принадлежат к поверхностям изотермических волн, то вблизи их колебания происходят смешанные; но на значительных расстояниях волна приближается к виду одной из изотермических волн, и в явлении обнаруживаются колебания продольные. Это заключение было выведено иным путём Пуассоном.
Нам остается объинтегрировать приведенные дифференциальные уравнения для сферы.
Для сферы в координатах, уже нами употреблённых, мы имеем:
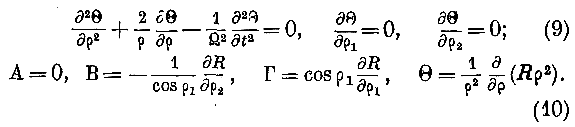
Подставляя величины В и Т в уравнение (5), получаем :
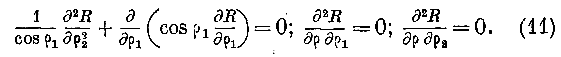
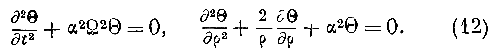
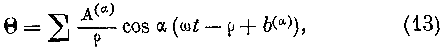
где суммирование совершается но индексу к.
Подставляя величину 0 в последнее из уравнений (10), интегрируя
u обращая внимание на уравнение (11), находим: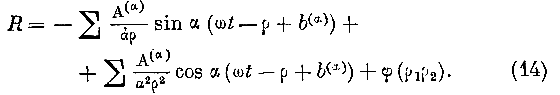
Последний член этого выражения должен равняться нулю, ибо при
p =оо будет /2 = 0. Второй член второй части выражения R отпадает для (> различных, и квадрат амплитуды, т. е. напряжение звука, изменяется обратно пропорционально квадрату расстояния.Между тем квадрат амплитуды кубического расширения следует тому жо закону для всякого р. Все эти выводы были получены Пуассоном иным путём.
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|
 |
