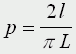
В вероятностных моделях смена состояний моделируемой системы определяется случайными величинами.
Событие называется случайным, если оно достоверно непредсказуемо. Случайность окружает наш мир и чаще всего играет отрицательную роль в нашей жизни. Однако есть обстоятельства, в которых случайность может оказаться полезной.
Одним из распространенных приближенных методов решения задач вычислительной математики является случайный метод, называемый метод Монте-Карло. Сущность метода заключается в том, что для решения какой-либо математической задачи, связанной с вычислением числа I, строится некоторая случайная величина ξ, такая, что математическое ожидание этой случайной величины E(ξ) является значением искомого решения. Проведя серию вычислительных экспериментов со случайной величиной ξ, мы можем найти приближенное решение как среднее значение результатов эксперимента.
С помощью этого метода можно найти площадь любой фигуры G, которая имеет сложный контур, который сложно описать аналитически или сложно проинтегрировать. Нужно вписать эту фигуру в фигуру известной площади, скажем в прямоугольник со сторонами a b и бросать точку на эту фигуру. Вероятность попадания точки в G будет равна отношению площадей.
Также с помощью случайного метода можно вычислить число π.
Для этого необходимо решить задачу Бюффона. Французский математик Бюффон (XYIII в.) определил, что если на поле, разграфленное параллельными прямыми, расстояние между которыми L, бросается наугад игла длиной l, то вероятность того, что игла пересечет хотя бы одну прямую, определяется формулой:
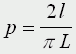
Эта задача дала способ вычисления числа π.
Действительно, если L=2l, то 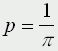
Таким образом, автором было вычислено 200 знаков после запятой числа π. Точность получаемого решения зависит от количества проведенных экспериментов.
Задачу Бюффона можно легко смоделировать на компьютере
Известно, что P=N1/N , где N - число бросаний, N1 - число пересечений иглы с линиями.
Как определить, пересекла игла прямую или нет? Положение иглы можно однозначно определить заданием координаты центра иглы y_0 из [-l/2,l/2] и угла α, задаваемых случайным образом
Тогда координаты концов иглы определяются по следующим формулам:
Условие пересечения прямой - y1*y2<0
На случайности основана "модель броуновского движения", которая используется для моделирования всевозможных хаотических движений частиц скажем движений молекул каких-либо газов или жидкостей, с помощью этой модели моделируются многие химические и физические процессы, проходящие в дискретных средах - в газах и жидкостях - явления диффузии, всевозможные потоки частиц, ветер, водопад, взрыв и т.д.
Есть точка на прямой, имеющая начальную координату x0, которая движется вправо или влево в зависимости от случайной величины r из интервала [0,1] если r>0,5, то точка делает шаг вправо x1=х0+h, в противном случае x1=x0-h. Шаг может быть как постоянный, так и переменный. Значение шага в свою очередь может быть случайное число из интервала [0,hmax].
Точка может двигаться по плоскости, может быть n точек - получается модель броуновского движения. Можно ввести различные скорости движения частиц, можно изменять условие, скажем если ri>0,8, то точка делает шаг вправо x1=х0+h, в противном случае x1=x0-h. - получим модель поступательного движения частиц вправо - стая комаров, подхваченных ветром. Если первоначально все частицы сконцентрировать в одной точке, а потом пронаблюдать их распространение - то это будет модель взрыва. Если провести вертикальную черту - перегородку, и частицы по разную строну перегородки закрасить разным цветом - получим модель диффузии - смешивания различных газов или жидкостей и т.д.
В модели броуновского движения не предусматривается столкновение частиц.
Если случайным образом задать первоначальное положение частиц, направление их движения и скорость и определить, что далее частица будет двигаться равномерно и прямолинейно до столкновения с другой частицей, а в случае столкновения произойдет зеркальное упругое отражение, то получим модель движения частиц, называемую моделью бильярдного шара. Эта модель описывает поведение идеального газа. С помощью этой модельки можно посчитать, допустим, давление газа на стенки сосуда - ограничить частицы прямоугольником (количество частиц установить пропорциональным плотности газа), предусмотреть зеркальное отражение частиц от стенок и посчитать число ударов в стенки сосуда. Давление газа будет пропорционально числу ударов о стенки.
|
|