Изображение – это, пожалуй, основной вид представления информации, которое воспринимается человеком. Изображения формируются на основе самых различных физических принципов самыми различными системами. В оптике – при помощи широкого спектра приборов от фотоаппарата до телескопа и микроскопа, в акустике при помощи набора микрофонов, в радиоастрономии системами антенн и т.д. Многообразие систем формирования изображений настолько велико, что их перечисление займет не одну страницу. При всем этом есть некоторые признаки, по которым мы узнаем, что данное многомерное распределение физических величин есть изображение. Мы не будем увлекаться философскими построениями на этот счет, т.к. наша утилитарная задача – это медицинские изображения, по которым врач ставит диагноз. Поэтому мы введем следующее определение:
Изображение — это распределение физических величин, которое имеет зрительную смысловую нагрузку.
Конечно, это очень условное и субъективное определение. Для кого-то композиции Кандинского бессодержательный набор линий, а для других они наполнены информацией. Но так и в медицинской практике, прежде чем, например, акустические изображения начнут давать информацию врачу о внутренних органах он должен достаточно долго практиковаться. Но в то же время нам необходимы какие-то математические свойства изображения, которых также можно предложить много. Мы, в дальнейшем, будем использовать ряд из них, что позволяет нам сформулировать математическое определение: Изображение — это некоторая многомерная функция 2-х, 3-х, 4-х переменных физических величин, отвечающих определенным свойствам:
1- Ограниченность носителя (не существует бесконечного изображения);
2- Неотрицательность
3- Ограниченность по величине, т.е. всегда максимальное значение функции, описывающей изображение меньше бесконечности.
В наше время, когда практически каждый студент должен уметь работать с различными пакетами программ обработки изображений, важно понимать какие основные классы преобразований изображений используются и чем они отличаются друг от друга.
Можно привести следующее, достаточно условное, деление видов обработки изображений:
1) Коррекция изображения
Коррекция геометрических искажений предполагает изменение по определенным правилам координат функций, не изменяя значений функций в каждой точке. Для двумерной функции это запишется следующим образом
![]() , где f(x,y) – изображение.
, где f(x,y) – изображение.
Такие преобразования применяются, например, при изменении масштаба изображений, устранение известных геометрических аберраций, вызванных системами формирования. Особенно широко данное преобразование используется в аэрофотосъемке. Можно найти множество других примеров коррекции изображений.
2) Улучшение визуального качества изображения
При обработке изображений часто осуществляют интерактивное изменение значений функции f(x,y).
![]() , т.е. локально изменяют значение функции, не изменяя координат (области задания).
, т.е. локально изменяют значение функции, не изменяя координат (области задания).
Фактически это ретушь, которую часто применяли и применяют фотографы. Для преобразований изображений такого рода существуют комплексы стандартных программ, которыми оснащены персональные компьютеры. Первые два метода практически не применяются при анализе медицинских изображений, т.к. субъективные преобразования могут привести к неправильному диагнозу.
3)Трансформация и фильтрация изображений
Данный тип обработки наиболее широко распространен при анализе изображений. Он основан на воздействии на функцию, описывающую изображение операторами различного типа – дифференциальными, сглаживающими и т.п. К таким же преобразованиям изображения относится и всевозможная фильтрация. Условно данный тип обработки можно представить в виде:
![]() , где А — известные законы преобразования.
, где А — известные законы преобразования.
В области такого улучшения качества изображения достигнуты самые большие успехи. Созданы большие пакеты программ, имеющие в своем архиве целые наборы линейных и нелинейных операторов. Огромное количество литературы посвящено именно данному виду обработки. При его использовании необходимы оценки параметров искажений и это используется при дальнейшей коррекции изображения. Фильтрация, дифференцирование и т.д. широко применяется при обработке экспериментальных изображений в том числе и медицинских. Необходимо только при разработке приборов не использовать слепо стандартные процедуры, т.к. их область применения, как правило, ограничена, и каждый раз их использование должно быть строго обосновано. Иначе возможны непредсказуемые преобразования изображения и, как следствие, плохая диагностика.
4) Реконструкция или восстановление изображений (в частности это и томография)
В отдельный вид обработки изображений необходимо выделить процесс компенсации искажений, вносимых в изображение в процессе формирования. Изображение всегда формируется некоторыми приборами, включающими в себя большое количество элементов его преобразующее. Таким образом, между предметом и изображением существует система формирования изображения, которая может очень сильно искажать предмет. Воздействием системы формирования изображения обусловлены такие его характеристики как разрешающая способность, контраст в передаче различных пространственных частот и т.п. В результате мы всегда получаем изображение отличное от функции описывающей объект. При этом снижается ценность полученной информации, следовательно, необходимо преобразовать изображение так, чтобы реконструировать (восстановить) функцию, описывающую объект. В дальнейшем для упрощения мы будем употреблять термин «реконструкция объекта» или «реконструкция изображения», понимая конечно, что объект в реалии есть нечто материальное и реконструировать его, используя изображение нельзя. Реконструкция изображения — это извлечение деталей в искаженном изображении при известной априорной информации о процессе формирования изображения и об объекте. Как правило этот тип обработки относится к обратным задачам математической физики, которые подразумевают получение изображения, максимально приближенного к объекту, с учетом свойств системы, формирующей изображение. Понимание в необходимости решения такой задачи в приборостроении пришло достаточно давно. Всегда оптики стремились создать микроскоп со сверхразрешением. В целом данная задача получила название – редукция к идеальному прибору.
Этот вид обработки изображений наиболее сложный и требует для своего решения привлечения серьезной математической подготовки и значительных вычислительных средств. Томография является как раз таким методом получения изображений. Неслучайно в названии метода звучит - реконструктивная компьютерная томография.
Процесс формирования изображения, как правило, записывают в операторном виде.
Оператор, напомним, это преобразование, осуществляющее трансформацию некоторой функции в функцию. В нашем случае, функцию, описывающую объект в функцию, описывающую изображение.
Пусть мы имеем двумерный объект ¦(x,y), его двумерное изображение q(x,h) и А — оператор, который воздействует на объект, тогда можно записать воздействие некоторого оператора на объект: ![]() .
.
Важно, чтобы оператор был известен. Иногда, оператор бывает сложным, т.е. последовательно действует несколько операторов. В этом случае получаем сложный процесс формирования изображения: ![]() n
n
В общем случае важен порядок воздействия операторов.
Суть задачи реконструкции: зная А, найти обратный оператор ![]() и подействовать на изображение, т.е. получить реконструированный объект:
и подействовать на изображение, т.е. получить реконструированный объект: ![]() , где
, где ![]() — изображение, которое максимально приближено к объекту.
— изображение, которое максимально приближено к объекту.
Процесс формирования изображения возможен двух видов:
1) Одноступенчатый метод формирования изображения (рисунок 2.1)
Этот метод часто встречается в повседневной жизни (фотоаппарат, телескоп, микроскоп).

Рисунок 2.1 - Одноступенчатый метод формирования изображения
Как правило, такой процесс формирования изображения описывается оператором в интегральной форме:
![]()
где ![]() – ядро интегрального оператора (определяется прибором, формирующим изображение и способом формирования изображения). Для оптических систем
– ядро интегрального оператора (определяется прибором, формирующим изображение и способом формирования изображения). Для оптических систем ![]() находится из теории дифракции.
находится из теории дифракции.
Как правило, при одноступенчатом методе формирования при хорошем качестве прибора изображение похоже на объект. Так обстоит дело в микроскопии, астрономии и т.д. Поэтому процесс реконструкции, т.е. редукции к идеальному прибору, в данном случае не применяется. Его используют только в уникальных случаях, когда хотят достигнуть сверхразрешения.
2) Двухступенчатый метод формирования изображения
Этот метод используется, когда нет возможности получить реальные измерения похожие на изображение. Поэтому они должны быть трансформированы, чтобы получить вид, удобный для визуального восприятия. Широко распространены два двуступенчатых способа получения изображения: томография и голография.
Двухступенчатый метод формирования изображения разберем на примере голографии.
Пусть есть объект ![]() и есть промежуточный регистратор — голограмма
и есть промежуточный регистратор — голограмма ![]() , представленные на рисунке 2.2. Рассмотрим освещение оптическим излучением.
, представленные на рисунке 2.2. Рассмотрим освещение оптическим излучением.
 |
Рисунок 2.2 – Схема голографии
Объект освещает поле Е, Еоб — отраженное поле от объекта.
![]() ,
,
где ![]() ,
,
![]() – волновое число,
– волновое число,
h – расстояние между плоскостью объекта и плоскостью голограммы.
В процессе записи на фотопластинке мы регистрируем поле замешанное с опорным полем, когерентным отраженному от объекта - Еоп :
![]()
![]()
Получившееся двумерное распределение интенсивности, фиксируемое как правило на фотопластинке, называется голограммой.
Визуально голограмма не несет смысловой нагрузки. Необходима обработка полученной информации, которая приводит к формированию изображения. Она выполняется на втором этапе и называется реконструкцией голограммы.
Таким образом можно выделить две ступени получения изображения:
Первая ступень: зарегистрировали некоторое распределение на промежуточный носитель, но не можем интерпретировать.
Вторая ступень: реконструкция изображения с промежуточного носителя.
Задача реконструкции изображения из голограммы осуществляется простым освещением голограммы оптическим излучением, идентичным по форме Еоп. Эта излучение называется восстанавливающим - Евос.
![]() ~
~![]() Þ
Þ ![]()
![]() ,
,
где ![]()
Можно показать, что после освещения голограммы в пространстве образуется изображение идентичное исходному объекту, которое мы и наблюдаем. Таким образом после второго этапа – реконструкции, мы получаем искомое изображение.
Полученное изображение, может быть связано с исходным объектом интегральным уравнением, ядро которого зависит от всех параметров голографического процесса:
![]()
Реконструированное изображение похоже на голографируемый объект. Двухступенчатый процесс подразумевает разработку оператора для реконструкции изображения. В случае голографии роль оператора реконструкции играет освещение голограммы восстанавливающим полем. Связь между объектом и изображением описывается интегральным уравнением.
Процесс формирования изображений описывает интегральными уравнениями. Введем некоторые понятия, которые нам потребуются для понимания их свойств.
Пространства функций:
 , функции интегрируемые на промежутке [a,b] (это почти все функции)
, функции интегрируемые на промежутке [a,b] (это почти все функции)
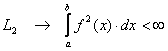 , множество функций интегрируемых в квадрате на [a,b].
, множество функций интегрируемых в квадрате на [a,b].
![]() все непрерывные функции, заданных на [a,b].
все непрерывные функции, заданных на [a,b].
Понятие изображений полностью укладывается в эти пространства.
Свойства оператора:
1) Линейность: ![]()
Воздействие двух функций независимо.
2) Непрерывность и Ограниченность: В чисто математическом смысле требование непрерывности означает, что если есть последовательность функций fn, сходящаяся к f, то действие оператора не нарушает сходимости. Для линейных операторов требования непрерывность и ограниченность совпадают. Они сводятся к выполнению условия ![]() , где k - действительная константа
, где k - действительная константа ![]() .
.
Не бывает изображений, которое было бы больше объекта по норме, умноженное на константу. Физический смысл условия ограниченности означает, что преобразованию изображения с ограниченной энергией соответствует изображение так же с ограниченной энергией.
3) Коммутативность (Коммутация с оператором сдвига)
Введем оператор сдвига, который действует на объект(![]() , где h – константа):
, где h – константа):
![]() . Коммутативность
. Коммутативность![]() с А означает, что их можно менять местами:
с А означает, что их можно менять местами:
![]() .
.
В оптике это свойство носит название изопланатичность или пространственная инвариантность.
Наиболее удобной формой записи изображения является интегральное — уравнение Фредгольма I - го рода:  , где
, где ![]() - ядро интегрального уравнения, описывающего процесс формирования изображения. В физике
- ядро интегрального уравнения, описывающего процесс формирования изображения. В физике ![]() называется функцией Грина, в оптике – функцией рассеяния точки, в радиотехнике – импульсной переходной характеристикой, чаще – аппаратной функцией.
называется функцией Грина, в оптике – функцией рассеяния точки, в радиотехнике – импульсной переходной характеристикой, чаще – аппаратной функцией.
Уравнение Фредгольма практически никто не решает. В случае коммутации данного интегрального оператора с оператором сдвига это уравнение может быть преобразовано к виду:  . В этом случае интегральное уравнение сводится к уравнению типа свертки.
. В этом случае интегральное уравнение сводится к уравнению типа свертки.
Операция свертки обладает свойствами:
1) коммутативностью ![]()
2) ассоциативностью ![]()
Теорема о Фурье - образе свертки: Если мы имеем свертку двух функций и можем ввести Фурье-образы от каждой из этих функций, то:

Фурье-образ обладает свойством обратимости и не зависит от сдвига, тогда функции ![]() и
и ![]() одинаково описывают формирование изображения, следовательно, такой вид записи носит характер фильтрации.
одинаково описывают формирование изображения, следовательно, такой вид записи носит характер фильтрации.
Понятие d - функции:
Вспомним d(х) - функцию: бесконечный импульс в точке, равной нулю. d(х) является обобщенной функцией и сама по себе, отдельно, не используется. Она используется только в интегральных записях (это есть ее определение):
 .
.
Это свойство называется иногда называется фильтрующим, и система формирования изображения является идеальной, когда ее весовая функция равна d - функции. В этом случае функция, описывающая изображение тождественна функции, описывающей объект.
Для реконструкции изображения нужно сконструировать обратный оператор, т.е. решить обратную задачу. Термины прямой и обратной задачи являются строго математическими.
При решении любой обратной задачи возникают три главных вопроса:
1. Существует ли решение основного интегрального уравнения
2. Если решение существует, то является ли оно единственным
3. Устойчиво ли решение, т.е. приводят ли малые изменения исходных данных к малым изменениям решения.
Если решение существует единственное и устойчивое, то задача называется корректно поставленная. Понятие корректной постановки задач математической физики было введено Ж.Адамаром и долгое время считалось, что задача всегда должна удовлетворять этим требованиям. Если задача не удовлетворяет им, то она называется некорректно поставленная или некорректная. Задачи реконструкции изображения, как правило, являются некорректно поставленными, так как не выполняется ни одно из вышеперечисленных условий поэтому долгое время считалось, что их решение невозможно. Однако, желание защиты диссертаций и получения финансирования научных работ, а главное требования практики заставляли ученых браться за решение этих задач и в конечном итоге привели к созданию теории решения некорректных задач.
Имея изображение мы всегда понимаем, что был объект, который «породил» зарегистрированный образ. Таким образом, существование входного сигнала не вызывает сомнений. Поэтому, если мы не можем найти решение, то это может быть вызвано двумя причинами:
1) Не так зарегистрировали информацию или малое количество, следовательно, произошла необратимая потеря информации.
2) Если решения задачи не существует, то это можно объяснить неадекватностью математической модели той реальной ситуации, которая соответствует процессу формирования изображения. Ведь надо помнит, что мы ищем не объект, а решение уравнения, которое описывает процесс формирования изображения.
Пусть у нас существует интегральное уравнение: 
Существование решения этого интегрального уравнения связано с условиями, которые накладываются на изображение ![]() , т.е. на процесс регистрации изображения, и на
, т.е. на процесс регистрации изображения, и на ![]() - ядро оператора формирования изображения.
- ядро оператора формирования изображения.
Будем рассматривать более простой случай – уравнение типа свертки (именно этот тип уравнений используется в томографии): 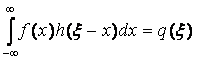 .
.
Напомним, что в этом случае оператор формирования изображения инвариантен сдвигу объекта. Применим преобразование Фурье к двум частям уравнения: ![]() , где
, где ![]() — Фурье образ функции, которую мы регистрируем и
— Фурье образ функции, которую мы регистрируем и ![]() - Фурье образ ядра интегрального уравнения нам известны. Фурье образ решения уравнения можно записать в виде:
- Фурье образ ядра интегрального уравнения нам известны. Фурье образ решения уравнения можно записать в виде: ![]() .
.
Для нахождения решения возьмем ОПФ (обратное преобразование Фурье):
![]() (2.1)
(2.1)
Это преобразование возможно при следующих ограничениях на функции, входящие в состав уравнения:
![]() (интегрируема в квадрате)
(интегрируема в квадрате)
![]() (линейно интегрируема)
(линейно интегрируема)![]()
![]() (интегрируема в квадрате)
(интегрируема в квадрате) ![]() , при любом ω.
, при любом ω.
Самым существенным из этих ограничений является ограничение на ![]() .
.
Решение, описываемое формулой (2.1) существует при ![]() ; если при каких либо ω -
; если при каких либо ω -![]() , то данные частоты не прошли через систему, т.е. в изображении нет полной информации об объекте. Формально мы не можем реконструировать объект, следовательно, решение обратной задачи не существует.
, то данные частоты не прошли через систему, т.е. в изображении нет полной информации об объекте. Формально мы не можем реконструировать объект, следовательно, решение обратной задачи не существует.
Рассмотрим вопрос о единственности решения. Предположим, что мы не знаем, есть у нас полный набор данных для восстановления или нет в этом случае мы, после выполнения формальных процедур, получим решение. Однако, необходимо доказать единственное ли оно или мы получили первое попавшееся решение, а оно не соответствует истинному.
Рассмотрим этот вопрос на примере, когда процесс формирования изображения описывается уравнением типа свертки (аналогично предыдущему случаю):
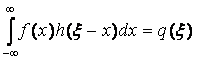 ,
,
или после преобразования Фурье: ![]() (2.2)
(2.2)
Предположим, что на некотором интервале ![]() , который ограничен
, который ограничен ![]() и
и ![]() , передаточная функция системы тождественно равна нулю:
, передаточная функция системы тождественно равна нулю: ![]() (рисунок 2.3)
(рисунок 2.3)
 |
В то же время на этом интервале ![]() . Тогда можно заметить, что если взять уравнение (2.2) и прибавить к функции F(ω) произвольную функцию
. Тогда можно заметить, что если взять уравнение (2.2) и прибавить к функции F(ω) произвольную функцию ![]() , которая равна нулю вне интервала
, которая равна нулю вне интервала ![]() , то вид функции G(ω) не изменится. В этом случае можно найти другое решение
, то вид функции G(ω) не изменится. В этом случае можно найти другое решение ![]() . Возможны два решения
. Возможны два решения ![]() и
и ![]() :
:![]() , где
, где ![]() Таким образом мы можем получить практически произвольное число решений (
Таким образом мы можем получить практически произвольное число решений (![]() может быть любая) интегрального уравнения типа свертки, так как к функции f(x) может быть добавлена d(x) , Фурье-образ которой равен нулю вне области W. Уравнение не имеет единственного решения также, когда Фурье-образ ядра в некоторых точках обращается в нуль.
может быть любая) интегрального уравнения типа свертки, так как к функции f(x) может быть добавлена d(x) , Фурье-образ которой равен нулю вне области W. Уравнение не имеет единственного решения также, когда Фурье-образ ядра в некоторых точках обращается в нуль.
Передаточные функции реальных систем часто имеют нулевые точки или области (даже самые простые оптические системы). Поэтому вопрос единственности и обоснования правильности решения необходим практически во всех случаях реконструкции реального изображения. Для однозначного восстановления изображения необходимы принципы отбора правильного решения. Для этого используют различную априорную информацию об объекте (то, что известно до эксперимента).
До сих пор мы считали, что функция q(![]() ) известна точно, но все наши реальные измерения осуществляются с некоторым шумом.
) известна точно, но все наши реальные измерения осуществляются с некоторым шумом.
Возьмем уравнение типа свертки. Условия на функции накладываются те же.
Пусть правая часть известна не точно и существует аддитивная шумовая составляющая: ![]()
![]()
Возьмем обратное преобразование Фурье и запишем решение:
![]()
Рассмотрим полученную добавку. Так как помеха носит случайный характер, то и ошибка точного решения носит случайный характер, следовательно, целесообразно оценить ее дисперсию: 
Р![]() (w) - спектральная плотность шума. Р
(w) - спектральная плотность шума. Р![]() (w)=
(w)=![]()
Если ![]() в каких-то точках, то
в каких-то точках, то ![]() ¥ и на изображении появляются ложные частоты в виде резких артефактов.
¥ и на изображении появляются ложные частоты в виде резких артефактов.
Но гораздо опаснее другой эффект. Как правило, Н(w) имеет зависимость, приведенную на рисунке 2.4:
Рисунок 2.4
Как правило, в реальной ситуации передаточная функция системы стремится к нулю при ![]()
 |
Возникновение ложных частот в изображении происходит, в основном, в области высоких частот. При этом, чтобы не потерять истинные высокие частоты, присущие объекту, необходимо использовать всю имеющуюся априорную информацию об объекте.
В практических задачах восстановления мы практически уверены в существовании решения и его единственности.
Неустойчивость решения является неотъемлемой частью этих задач и делает их всегда некорректно поставленными. Математики придумали много эмпирических решений, но задачи были частными.
В 60-е годы Тихонов А.А. разработал общие принципы решения таких задач. (Метод реализации Тихонова используется во всех томографах).
При реконструкции изображения идет увеличения шума. Следовательно, появляются ложные пространственные частоты. Их нужно подавить.
В первую очередь были разработаны эвристические методы решения задачи реконструкции изображения. Для рассмотрения процесса реконструкции изображения в присутствии шумов представим процесс формирования изображения и его последующей реконструкции в виде последнего воздействия двух линейных систем на входной сигнал, схема представена на рисунке 2.5. Пусть имеется входной сигнал f(x), он входит в систему формирования изображения с импульсным откликом h, следовательно, на выходе q(x), который будет сверткой линейных систем
 |
Рисунок 2.5 - Процесс реконструкции изображения в присутствии шумов

h![]() (x) – реконструирующая система
(x) – реконструирующая система
После реконструкции получаем:

Чтобы реконструкция была идеальной, необходимо, чтобы h![]() (х)=d(х), тогда
(х)=d(х), тогда ![]()
Если мы применим преобразование Фурье: Н![]() (w)=const, т.е. получаем идеальную передаточную функцию и, как следствие, идеальное изображение при реконструкции (рисунок 2.6).
(w)=const, т.е. получаем идеальную передаточную функцию и, как следствие, идеальное изображение при реконструкции (рисунок 2.6).
 |
Рисунок 2.6
В частотной области ![]()
![]() или
или ![]() получаем идеальную передаточную функцию (идеальное изображение).
получаем идеальную передаточную функцию (идеальное изображение).
Зависимость при представлена на рисунке 2.7.
 |
Рисунок 2.7
На практике наличие шума приводит к необходимости вводить некоторые ограничения на полосу пропускания частот при реконструкции, т.к. при ![]()
![]() , следовательно, возможно бесконечное увеличение шума. Для его ограничения вводится граничная частота ωг. Она выбирается из априорных требований к системе формирования изображений и определяется максимальной пространственной частотой, которую мы хотим пропустить через систему. На практике иногда говорят о разрешающей способности прибора, которая и определяется этой частотой. Математически это эквивалентно ограничению пределов интегрирования при обратном преобразовании Фурье. Поэтому вводят индикаторную
, следовательно, возможно бесконечное увеличение шума. Для его ограничения вводится граничная частота ωг. Она выбирается из априорных требований к системе формирования изображений и определяется максимальной пространственной частотой, которую мы хотим пропустить через систему. На практике иногда говорят о разрешающей способности прибора, которая и определяется этой частотой. Математически это эквивалентно ограничению пределов интегрирования при обратном преобразовании Фурье. Поэтому вводят индикаторную

![]() , Следовательно
, Следовательно ![]()
Ограничение полосы частот промежутком (-ωг;ωг) эквивалентно ограничению пределов интегрирования при обратном преобразовании Фурье.
Увеличение ωг ведет к увеличение шума, а уменьшение ωг ведет к невозможности восстановления высоких частот, т.е. изменяя значения ωг можно изменять соотношение между качеством восстановления и величиной шума.
Однако резкая граница в частотной области приводит к возникновению в изображении существенных артефактов, т.н. «дребезга» частот. Поэтому на практике применение индикаторной функции P(ω) невозможно и было предложено ввести еще один параметр в частотной области – частота среза ωс. В пределах (-ωс;ωс) передаточная функция умножается на индикаторную функцию Р(ω), а между ωс и ωг изменим функцию ![]() .
.
На отрезке (-![]() ;
;![]() ) ®
) ® ![]() , а на углах она закругляется и на ωг -
, а на углах она закругляется и на ωг -![]() , как показано на рисунке. Введение функции К(w) является компромиссом между уменьшением шума и увеличением качества на высоких частотах. В таком случае уравнение для реконструированного изображения будет иметь вид:
, как показано на рисунке. Введение функции К(w) является компромиссом между уменьшением шума и увеличением качества на высоких частотах. В таком случае уравнение для реконструированного изображения будет иметь вид:
![]()
где функция К(w) – сглаживает любые точки выброса и имеет разные виды.
Таким образом можно бороться и с неоднозначностью и с единственностью решения. Функция К(w) получила название “окна” (окна Чебышева, окна Хейминга, окна Гаусса).
В дальнейшем, используя эту идею каждый ученый, исходя из своей задачи выбирал функцию окна. Как правило, это определялось видом передаточной функции, спектральными характеристиками сигнала и шума, учитывалась конечная цель : увеличить разрешающую способность или минимизировать шум и т.д.
У функции окна К(w) всегда есть параметр, например, у фильтра Гаусса  ; изменяя уравнение окна и параметр, можно найти свой «оптимальный» фильтр. Умножение передаточной функции инверсного фильтра на К(w) соответствует отысканию сглаженного решения f(x). При выборе формы весовых функций (окон) часто требуется не только хорошая аппроксимация функции
; изменяя уравнение окна и параметр, можно найти свой «оптимальный» фильтр. Умножение передаточной функции инверсного фильтра на К(w) соответствует отысканию сглаженного решения f(x). При выборе формы весовых функций (окон) часто требуется не только хорошая аппроксимация функции ![]() , но и такое сгибание этой функции (наклон), при котором передаточная функция стремится к нулю при w®wг. Это необходимо, чтобы не получить большого усиления помехи.
, но и такое сгибание этой функции (наклон), при котором передаточная функция стремится к нулю при w®wг. Это необходимо, чтобы не получить большого усиления помехи.
У эвристического метода 2 недостатка:
1) Чтобы найти оптимальный фильтр нужно перебрать много фильтров и параметров
2) Неизвестно, когда остановиться, т.е. нет критерия качественности изображения.
Для того, чтобы исключить недостатки эвристического метода, и формализовать метод решения таких задач, Тихонов предложил метод регуляризации (метод регуляризации Тихонова).
Стремление избавиться от произвольных факторов и определить общие методы решения некорректно поставленных задач привело к разработке метода регуляризации решения и понятия регулирующего оператора. Регуляризация решения состоит в построении семейства обратных операторов, зависящих от некоторого числового параметра a (параметр регуляризации). Каждый оператор семейства дает решение корректной задачи, причем при a®0 ошибка в измерениях данных ®0 одновременно, реконструируемое изображение стремится к истинному решению (к объекту).
Запишем уравнение типа свертки
![]()
Решение:
![]()
Тихонов ввел функцию:
![]()
![]() ‑ некий оператор, воздействующий на q(x),эквивалентно введению К(w).
‑ некий оператор, воздействующий на q(x),эквивалентно введению К(w).
Чтобы найти точное решение, нужно найти условия, которым должна удовлетворять функция R(w,a).
Рассмотрим свойства, которым должна отвечать функция R(w,a):
Оператор является регуляризирующим, если функция R удовлетворяет следующим условиям:
1) R(w,a) должна быть определена на всей частотной оси для в области -¥<w<¥, ![]() (на всей вещественной оси)
(на всей вещественной оси)
2) Для любого ![]() и
и ![]() ;
; ![]()
3) Для любых ![]() : R(w,a)-четная по w,
: R(w,a)-четная по w,
4) Для любых![]() : R(w,a)®0 при êw÷ ®¥
: R(w,a)®0 при êw÷ ®¥
5) При α→0 : R(w,a) не убывая, стремится к единице (не может быть колебаний и осцилляций и функция должна возрастать)
6) Для любых ![]() :
: ![]() (иначе не посчитаем обратное преобразование Фурье)
(иначе не посчитаем обратное преобразование Фурье)
7) Для любых w¹0: R(w,a)®0 при a®¥.
Все свойства интуитивно понятны. Если “окно” не будет удовлетворять этим условиям, то не будет решения, т.е. ограничен класс выбора функций. Функция R(w,a), удовлетворяющая этим условиям, называется стабилизирующим множителем.
w,a) можно представить в виде:

Удобно изменять a, как отдельное число, которое изменяется от 0 до ¥.
Такому R(w,a) соответствует передаточная функция восстанавливающего фильтра:
 .
.
где Q(w)- неотрицательная четная функция, которая отвечает свойствам:
1) Q(w)>0, при w¹0
Q(0)³0
2) Q(0)³С>0 при достаточно больших ω :
Если мы используем такую функцию Q(w), то можем получить некий стабилизатор R(w,a). Простейший вид Q(w):
Вид функции ![]() r>0
r>0
Тихонов доказал теорему, что решение 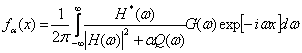
то, перебирая a от 0 до ¥, обязательно найдется решение, минимизирующее разницу между ƒ и q:
 ,
,
где А- стабилизирующий функционал, который зависит от a и Q.
Нужно, чтобы изображение от объекта отличалось на конечную величину. Тихонов доказал, что при выборе a перебором, можно добиться наличия устойчивого решения.
Реально процедура реконструкции объекта с использованием регуляризации Тихонова строится следующим образом:
1) Выбирается некий стабилизатор Q; как правило ![]() >0, строится по этому алгоритму решение.
>0, строится по этому алгоритму решение.
2) После выбора Q, значение параметра регуляризации находится по невязке, если мы оцениваем отклонение правой части уравнения в метрике ![]() , то невязка определяется следующей формулой:
, то невязка определяется следующей формулой:
 .
.
где А – оператор формирования изображения,
![]() − реконструированное изображение,
− реконструированное изображение,
q – зарегистрированное изображение.
Сейчас при помощи невязки рассчитывается среднеквадратичное отклонение между изображением, измеренным в процессе наблюдения, и изображением, полученном в системе в предположении, что объектом является функция ![]() .
.
Тихонов доказал, что если следовать его процедуре, то всегда существует a, при которой невязка min. Как правило: a=0,5¸2.
Если все подобрано правильно, то невязка равна среднеквадратичному отклонению функции G(w).
![]() ‑ среднеквадратичная погрешность измерения изображения.
‑ среднеквадратичная погрешность измерения изображения.
Есть один частный случай метода регуляризации Тихонова: винеровская оптимальная фильтрация.
Определим вид стабилизирующего множителя R в случае, когда при решении задачи реконструкции изображения используется дополнительная априорная информация о статистических характеристиках изображения и шума.
Точные решения и изображения: ![]() .
.
Но на самом деле измеряем: ![]() .
.
И есть априорная информация о спектральных плоскостях изображения и шума: ![]() .
.
Оказалось, что из этих априорных информаций можно найти:
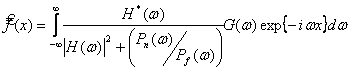 .
.
Если сравнить эту формулу с предыдущей (решение Тихонова), увидим, что здесь:
 ,
,
не зависит от a и ![]() .
.
К сожалению, спектр плотности объекта изображения в медицине почти не известен (Винер выводил свое уравнение для радиосигнала).
Достоинства винеровской фильтрации:
1) нет зависимости от a,
2) Четко задано Q(a)
Оптимальный фильтр Винера позволяет получить изображение, близкое к истинному, в смысле минимального среднеквадратичного отклонения при условии, что спектр плотности мощности изображения и шума априорно известны.
Методы реконструкции изображений, представленные в таблице 2.1 и представляющие собой некорректную задачу, решаются только при привлечении априорной информации о классе исследуемых объектов и характере искажения. Поэтому и называется реконструкцией при присутствии априорной информации.
Таблица 2.1 - Методы реконструкции изображений
| Наименование метода |
Передаточная функция |
Стабилизирующий множитель |
Вид частотной характеристики |
|
|
|
1 |
|
|
|
|
1, çwï£w 0, çwï>w |
Продолжение таблицы 2.1 - Методы реконструкции изображений
|
|
|
|
|
|
|
|
К(w,a) |
|
|
|
|
|
|
|