Рентгеновское излучение представляет собой электромагнитные волны, энергия фотонов которых лежит на энергетической шкале между ультрафиолетовым излучением и гамма-излучением, что соответствует длинам волн от 10-4 до 102Å (от 10-14 до 10-8 м).
Энергетические диапазоны рентгеновского излучения и гамма-излучения перекрываются в широкой области энергий. Оба типа излучения являются электромагнитным излучением и при одинаковой энергии фотонов — эквивалентны. Различие лежит в способе возникновения — рентгеновские лучи испускаются при участии электронов (либо в атомах, либо свободных) в то время как гамма-излучение испускается в процессах девозбуждения атомных ядер. Фотоны рентгеновского излучения имеют энергию от 100 эВ до 250 кэВ, что соответствует излучению с частотой от 3·1016 Гц до 6·1019 Гц и длиной волны 0.005 - 10 нм (общепризнанного определения нижней границы диапазона рентгеновских лучей в шкале длин волн не существует). Мягкий рентген обладает наименьшей энергией фотона и частотой излучения (и наибольшей длиной волны), а жесткий рентген обладает наибольшей энергией фотона и частотой излучения (и наименьшей длиной волны).
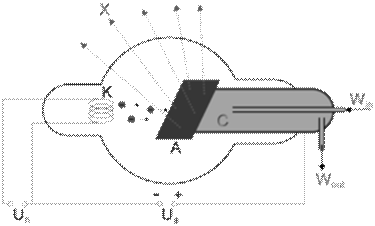
Рентгеновское излучение получают, как правило при помощи специализированных вакуумных приборов – рентгеновских трубок. Схематическое изображение рентгеновской трубки представлено на рисунке 5.1
X - рентгеновские лучи, K - катод, А - анод (иногда называемый антикатодом), С - теплоотвод, Uh - напряжение накала катода, Ua - ускоряющее напряжение, Win - впуск водяного охлаждения, Wout - выпуск водяного охлаждения
Рисунок 5.1 - Схематическое изображение рентгеновской трубки.
Рентгеновские лучи возникают при сильном ускорении заряженых частиц (в основном электронов) либо же при высокоэнергетичных переходах в электронных оболочках атомов или молекул. Оба эффекта используются в рентгеновских трубках, в которых электроны, испущенные раскалённым катодом, ускоряются (при этом рентгеновские лучи не испускаются, т.к. ускорение слишком мало) и ударяются об анод, где они резко тормозятся (при этом испускаются рентгеновские лучи: т.н. тормозное излучение) и в то же время выбивают электроны из внутренних электронных оболочек атомов металла из которого сделан анод. Пустые места в оболочках занимаются другими электронами атома. При этом испускается рентгеновское излучение с определенной, характерной для материала анода, энергией (характеристическое излучение, частоты определяются законом Мозли:
![]() ,
,
где
Z - атомный номер элемента анода,
A и B - константы для определённого значения главного квантового числа n электронной оболочки).
В настоящее время аноды изготовляются главным образом из керамики, причём та их часть, куда ударяют электроны, — из молибдена. В процессе ускорения-торможения 1% энергии идёт на рентгеновское излучение и 99% энергии идёт на тепловыделение.
Рентгеновское излучение можно получать также и на ускорителях заряженных частиц. Т.н. синхротронное излучение возникает при отклонении пучка частиц в магнитном поле, в результате чего они испытывают ускорение в направлении перпендикулярном их движению. Синхротронное излучение имеет сплошной спектр. При соответствующим образом выбранных параметрах (величина магнитного поля и энергия частиц) в спектре синхротронного излучения можно получить и рентгеновские лучи.
При прохождении рентгеновских лучей через какое-нибудь твердое, жидкое или газообразное тело они взаимодействуют с электронами, а при очень большой жесткости - и ядрами атомов элементов, которые входят в состав вещества и при этом теряют часть своей энергии.
При этом можно выделить следующие виды взаимодействия
1. истинное поглощение, т.е. превращения их энергии в другие виды энергии;
2. рассеяние, т.е. изменение направления распространения с изменением длины волн.
Первичными элементарными процессами истинного поглощения, т.е. преобразования его энергии в кинетическую энергию электронов, являются:
3. фотоэлектрический эффект – вырывание электронов из атомов поглощающего вещества и сообщение им кинетической энергии;
4. Комптон - эффект – рассеяние с изменением длины волны и передачей части энергии фотона рассеивающему электрону;
5. образование пар элементарных зарядов – электрона и позитрона – и сообщение им кинетической энергии.
Эти виды взаимодействия схематически показаны на рис. 5.2 и более детально рассматриваются ниже.
| а) |
| б) |
| в) |
Рисунок 5.2 - Важнейшие виды взаимодействия фотонов с веществом
Поглощение в результате фотоэффекта заключается в том, что энергия квантов рентгеновского излучения затрачивается на выравнивание электронов из атомов поглощающего вещества и сообщение им кинетической энергии.
Число вырываемых электронов, так называемых фотоэлектронов, пропорционально интенсивности рентгеновских лучей, а энергия их зависит от длины лучей и определяется уравнением:
![]() ,
,
где:
![]() - кванты энергии рентгеновских лучей, имеющих частоту ν;
- кванты энергии рентгеновских лучей, имеющих частоту ν;
Wэ – работа вырывания электрона;
![]() - кинетическая энергия фотоэлектрона:
- кинетическая энергия фотоэлектрона:
при скоростях электронов, сравнимых со скоростью света, выражение для кинетической энергии электронов, вытекающее из принципа относительности, имеет вид :
 ,
,
где ![]() - отношение скорости электрона ν к скорости света с.
- отношение скорости электрона ν к скорости света с.
Вообще можно различать следующие три случая вырывания электронов:
1. Вырывание электронов, слабо связанных с атомами (периферические электроны), т.е. ионизация в наружном слое.
Эти фотоэлектроны обладают наибольшими энергиями, так как работа удаления их мала (несколько электронвольт).
2. В трех случаях, когда кванты ![]() рентгеновских лучей, падающих на данное тело, насколько велики, что они могут вырвать электроны из внутренних слоев атомов поглощающего вещества, возникают фотоэлектроны, обладающие значительно меньшими энергиями, и одновременно возникает характеристическое рентгеновское излучение.
рентгеновских лучей, падающих на данное тело, насколько велики, что они могут вырвать электроны из внутренних слоев атомов поглощающего вещества, возникают фотоэлектроны, обладающие значительно меньшими энергиями, и одновременно возникает характеристическое рентгеновское излучение.
То, что эти фотоэлектроны обладают относительно малыми энергиями, объясняется тем, что работа вырывания электронов Wэ из внутренних слоев атома велика; следовательно, значительная часть энергии кванта ![]() затрачивается на вырывание внутриатомных электронов, и только остаток ее идет на сообщение им кинетической энергии.
затрачивается на вырывание внутриатомных электронов, и только остаток ее идет на сообщение им кинетической энергии.
Поглощение рентгеновских лучей и вырывание электронов этого рода происходит особенно сильно тогда, когда длина волны первичных лучей немного меньше длины волны характеристического излучения атомов поглощающего тела. С дальнейшим уменьшением длины волны падающих лучей поглощение и интенсивность вторичного характеристического излучения ослабевают.
3. Анализ распределения (числа) фотоэлектронов по скоростям показал, что относительное число фотоэлектронов второго рода слишком велико, того же порядка, как и число фотоэлектронов первого рода.
Это противоречие было разъяснено опытами Оже и др., которые фотографировали пути фотоэлектронов в камере Вильсона. Они обнаружили, что очень часто из одной точки (на фотографии) выходит несколько (два или четыре) фотоэлектрона, причем траектория (длина пробега) одного из них зависит, а траектории остальных не зависят от частоты падающего излучения и малы по сравнению с длиной пути первичных фотоэлектронов.
Появление парных траекторий Оже объяснил многократной ионизацией атомов. Теория сложного фотоэффекта подтверждается измерениями Оже и других не только качественно, но и количественно.
Оказывается, что сложный фотоэффект происходит очень часто, причем в атомах с малым атомным номером многократная ионизация наблюдается чаще, и переходы электронов из удаленных уровней на внутренний в большинстве случаев происходят без испускания рентгеновских лучей.
Процесс рассеяния рентгеновских лучей состоит в том, что первичные лучи при попадании на вещество отклоняются от своего первоначального направления и рассеиваются по всем направлениям.
Существуют две теории рассеяния рентгеновских лучей:
1. классическая теория, которая основана на исследованиях рассеяния относительно мягких рентгеновских лучей, показавших, что жесткость рассеянного излучения совпадает с жесткостью первичных лучей;
2. квантовая теория, предложенная Комптоном и Дебаем, основана на более поздних исследованиях рассеяния жесткого излучения показавших, что жесткость рассеянного излучения меньше жесткости первичного излучения.
По классическим представлениям явление рассеяния заключается в том, что первичные лучи вызывают вынужденные колебания слабо связанных электронов рассеивающего тела, которые сами становятся при этом центрами, излучающими вторичные рассеянные лучи той же длины волны. Исходя из таких представлений можно найти интенсивность лучей, рассеянных одним электроном.
Электрическая составляющая Ер поля падающей электромагнитной волны, которую примем линейно поляризованной, сообщает электрону ускорение
![]() . (5.1)
. (5.1)
С другой стороны, известно, что общий поток энергии, излучаемый электроном, движущимся с ускорением α, т. е. интенсивность излучения, равен:
![]() . (5.2)
. (5.2)
Подставляя в (5.2) значение α из (5.1), имеем:
![]() . (5.3)
. (5.3)
Выражая величину Ер- напряженность электрической составляющей волны попадающих лучей – через их интенсивность, исходя из уравнения Умова - Пойнтинга
![]()
![]() , (5.4)
, (5.4)
получаем окончательное выражение для интенсивности рассеянного излучения одним электроном:
![]() . (5.5)
. (5.5)
а) Из уравнения (5.5) легко определить коэффициент рассеяния одного электрона σэл т.е. отношение интенсивности рассеянного излучения Is к интенсивности падающих лучей Iр:
![]() . (5.6)
. (5.6)
б) Так как каждый атом рассеивающего тела содержит Z электронов, то, принимая , что рассеяние отдельными электронами происходит независимо друг от друга, можно считать что общее рассеяние, производимое одним атомом, равно сумме рассеяние отдельных электронов, и атомный коэффициент рассеяния выразится формулой:
![]() . (5.7)
. (5.7)
в) Если в 1 см3 рассеивающего тела содержится n атомов, то на
![]()
и линейный коэффициент рассеивания равен:
![]() , (5.8)
, (5.8)
где:
n – число атомов в единице объема.
г) Наконец, относятся к единице массы (1г), получим выражение для массового коэффициента рассеяния, разделив выражение (5.8) на плотности вещества ρ:
![]() . (5.9)
. (5.9)
В этом выражении ![]() можно выразить через число Авогадро N и атомный вес А, так как число атомов в
можно выразить через число Авогадро N и атомный вес А, так как число атомов в ![]() равно
равно ![]() :
:
![]() . (5.10)
. (5.10)
Подставляя числовые значения для N, e, m и с , имеем :
![]()
![]() , ( 5.11)
, ( 5.11)
т.е. массовый коэффициент рассеяния не зависит ни от длины волны первичных лучей, ни от рода рассеивающего вещества, так как отношение ![]() для всех элементов, кроме водорода, сохраняет почти постоянное значение, равное половине.
для всех элементов, кроме водорода, сохраняет почти постоянное значение, равное половине.
Кроме величины коэффициента рассеяния, можно найти также зависимость интенсивности рассеянного излучения от направления для поляризационного и неполяризованного первичного излучения. Для определения рассеяния в произвольном направлении в случае поляризованного первичного излучения разложим вектор электрического поля падающей электромагнитной волны на две составляющие - параллельную и перпендикулярную данному направлению. Тогда интенсивность рассеянного излучения в этом направлении будет пропорциональна квадрату перпендикулярной составляющей электрического вектора поля, так, как электрон, двигающийся с ускорением, не излучает в направлении ускорения.
Если мы имеем неполяризованный луч, то интенсивность рассеянного излучения в определенном направлении может быть определена следующим образом.
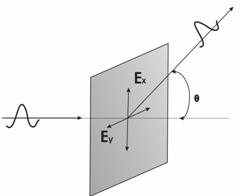
Рисунок 5.3. К выводу формулы (5.17)
Пусть направление неполяризованного излучения и направление рассеянного совпадают с плоскостью рисунка 5.3 и образуют между собой угол θ. Известно, что всякое неполяризованное излучение можно разложить на два перпендикулярных друг другу поляризованных компонента. Электрический вектор одного компонента направляем так, чтобы он совпал с плоскостью первичного и рассеянного лучей (с плоскостью рисунка), а вектор другого компонента – перпендикулярно этой плоскости. Если напряженность поля в обоих направлениях Ех и Еу, то
![]() ( 5.12)
( 5.12)
или, так как ввиду полной неполяризованности падающих лучей
![]() ,
,
то
![]() . (5.13)
. (5.13)
Тогда интенсивность рассеянного излучения в направлении θ от колебаний в направлении Ех будет:
![]() ( 5.14)
( 5.14)
и от колебаний в направлении Еу :
![]() . (5.15)
. (5.15)
Полное рассеяние в направлении θ равно сумме этих рассеяний, т.е. учитывая (5.13):
![]() (5.16)
(5.16)
или, заменяя Ер через Ip (5.4), получаем:
![]() . (5.17)
. (5.17)
Множитель ![]() , называемый поляризационным множителем, показывает что наибольшее рассеяние происходит в направлении первичного пучка и в прямо противоположном, а наиболее слабое- в плоскости, перпендикулярной к первичному пучку.
, называемый поляризационным множителем, показывает что наибольшее рассеяние происходит в направлении первичного пучка и в прямо противоположном, а наиболее слабое- в плоскости, перпендикулярной к первичному пучку.
Указанные в предыдущем параграфе закономерности рассеяния согласно исследованиям Комптона не подтверждаются в случае рентгеновских лучей с очень короткой длиной волны (начиная с λ = 0,3Å), а именно, с уменьшением длины волны наблюдается уменьшение коэффициента рассеяния и увеличение длины волны рассеянного излучения. Эти факты не могут быть объяснены с точки зрения классической теории. Согласно квантовой теории при рассеянии первичных рентгеновских лучей имеет место следующее явление.
При взаимодействии кванта лучистой энергии hν1 со свободным электроном освещаемого тела вместо кванта hν1 возникает новый квант hνs< hν1 и из тела вылетает электрон с определенной скоростью (зависящей от длины волны падающих лучей и направления вылета), так называемой «электрон отдачи».(0,3 Å = 0,3 · 10-10мм.)

Рисунок 5.4. Схема взаимодействия фотона со свободным электроном
Схема такого взаимодействия дана на рисунке 5.4, из которой видно, что рассеяние можно трактовать как своего рода упругий удар между падающим квантом hν1 и рассеивающим электроном m. При этом квант сообщает электрону импульс и передает ему часть своей энергии, а сам продолжает движение под углом φ к направлению первоначального движения, обладая уже меньшей энергией, т.е., с меньшей частотой или большей длиной волны.
Таким образом, «соударение» кванта с неподвижным свободным электроном аналогично соударению частиц. Отличие заключается только в том, что рассеянный квант hνs (фотон) летит со скоростью света, т.е. его скорость после соударения не меняется. Поэтому уменьшение энергии фотона проявляется в уменьшении его «массы». Так как массе электрона передается энергия и импульс, то изменяется не только энергия фотона, но и направление его движения.
Согласно теории Комптона коэффициент рассеяния σ связан с классическим коэффициентом рассеяния σо формулой:
![]() , ( 5.18)
, ( 5.18)
где
![]() .
.
Так, как при рассеянии квантов жестких лучей части их энергии передается электронам отдачи, а остальная часть рассеивается, то коэффициент рассеяния σ следует рассматривать как сумму двух коэффициентов – одного, учитывающего передачу энергии электрону отдачи, так называемого электронного коэффициента отдачи σе и второго, учитывающего рассеяние, коэффициента истинного рассеяния σs:
![]() ,
,
где
![]() ;
; ![]() (5.18)
(5.18)
В предыдущих параграфах были рассмотрены первичные процессы, происходящие при взаимодействии рентгеновского излучения с веществом, а именно, возникновение фотоэлектронов и характеристического излучения при поглощении и электронов отдачи и рассеянного излучения – при рассеянии. Очевидно, возникшие быстрые электроны и характеристическое и рассеянное излучение будут также взаимодействовать с веществом облучаемого тела.
Дальнейшее взаимодействие возникающих квантов излучения аналогично уже рассмотренному, т.е. рассеянный или характеристический квант может или вырвать вторичный фотоэлектрон, или снова рассеяться на более или менее удаленном электроне, или может совсем выйти из рассматриваемого объема поглощающего тела.
Первичные фотоэлектроны и электроны отдачи поглощаются веществом поглотителя в области, окружающей место их возникновения. Электроны, влетающие в атом, могут или пройти сквозь него, или поглотиться им.
Прохождение через атом связано с небольшой потерей энергии летящим электроном, которая расходуется на отделение вторичных электронов. Этот процесс может повторяться сотни и тысячи раз, при этом отделяется большое число вторичных электронов, а скорость первичного электрона – постепенно уменьшается до тех пор, пока он не соединится с каким-либо атомом и не отдаст ему сохранившуюся к этому моменту свою кинетическую энергию, которая переходит в теплоту.
Резкое торможение первичного фотоэлектрона, сопровождающееся излучением кванта рентгеновского излучения, происходит чрезвычайно редко, так же как и при торможении электронов на аноде трубки.
Вторичные электроны, освобождаемые первичными фотоэлектронами и электронами отдачи, имеют небольшие скорости, быстро затормаживаются и в редких случаях могут вызвать более медленные третичные электроны.
Все вторичные и третичные электроны поглощаются облучаемым веществом, и их энергия переходит в теплоту.
Полная цепь превращения энергии, происходящих при взаимодействии рентгеновских лучей с веществом, может быть представлена в упрощенном виде следующей схемой:
 |
Наибольшая толщина слоя, которую могут пролететь некоторые наиболее быстрые фотоэлектроны, называется «предельной толщиной». Она зависит от начальной скорости первичных фотоэлектронов и обратно пропорциональна плотности поглощающего вещества.
Если пропустить узкий параллельный пучок однородных рентгеновских лучей, т.е. обладающих одной длиной волны λ, через слой какого-нибудь вещества толщиной D сантиметров (рисунок 5.5), то по мере пропорциональности лучей в этот слой интенсивность пучка будет уменьшаться вследствие поглощения и рассеяния.

Рисунок 5.5 - К выводу закона рентгеновских лучей
Пусть Iх – интенсивность пучка лучей, проходящих через элементарный слой толщиной dх, отстоящий от поверхности поглощающего тела х сантиметров; тогда уменьшение интенсивности dIх внутри этого слоя будет пропорционально интенсивности пучка Iх , входящего в этот элементарный слой, и толщине этого слоя dх:
![]()
![]() (5.19)
(5.19)
где
μ - коэффициент пропорциональности, называется линейным коэффициентом ослабления, который зависит от длины волны и рода поглощающего вещества.
Разделяя переменные в (5.19) и интегрируя по х от 0 до D, получаем:

![]() ;
; ![]() ,
,
или
![]() , (5.20)
, (5.20)
где I0 – интенсивность падающих лучей и ID – интенсивность лучей, прошедших через слой толщиной D.
Так, как ослабление первичного пучка лучей обусловлено поглощением и рассеянием, то коэффициент ослабления можно рассматривать как сумму двух коэффициентов - линейного коэффициента поглощения τ и линейного коэффициента рассеяния σ, так, что
![]() .
.
Следовательно, уравнение (5.20) можно переписать так:
![]() . (5.21)
. (5.21)
Из приведенных формул видно, что ослабление рентгеновских лучей увеличивается очень быстро с увеличением толщины поглощающего слоя. В таблице 5.1 приведены экспериментальные данные ослабления интенсивности однородного пучка лучей при длине волны λ =0,71Å в алюминиевых пластинах разной толщины.
Таблица 5.1
| Толщина слоя D, мм |
0,1 |
0,5 |
1,0 |
2,0 |
3,0 |
4,0 |
| Отношение I : I0 |
0,87 |
0,5 |
0,25 |
0,06 |
0,015 |
0,004 |
Зависимость коэффициентов ослабления μ, поглощения и τ и , рассеяния σ от химической природы поглощающего вещества принимает простую форму, если их отнести не к единице длины (пути прохождения через поглощающее вещество), а к единице массы этого вещества, т. е если значения этих коэффициентов поделить на плотность ρ рассматриваемого вещества. Коэффициенты ![]() называются массовым и коэффициентами ослабления, поглощения и рассеяния.
называются массовым и коэффициентами ослабления, поглощения и рассеяния.
Массовой коэффициент рассеяния согласно классической теории, формула (5.11), не зависит от длины волны лучей и слабо уменьшается с ростом атомного номера рассеивающего элемента. В действительности массовый коэффициент рассеяния увеличивается с увеличением атомного номера рассеивающего вещества следующим образом:
Таблица 5.2
| Z |
0,18-0,2 |
16-22 |
22-30 |
31-35 |
36-39 |
40-44 |
44-54 |
54-92 |
|
|
0,18 |
0,18-0,2 |
0,2-0,3 |
0,3-0,4 |
0,4-0,5 |
0,5-0,6 |
0,6-0,7 |
0,7 |
Массовой коэффициент поглощения сильно зависит от длины волны лучей и от атомного номера вещества поглощающего тела. Он определяется экспериментально следующим образом.
Закон ослабления пучка однородных лучей определяется формулой:
![]() . (5.22)
. (5.22)
Измеряя интенсивность Ix пучка лучей, прошедших через слой какого-либо вещества различной толщины х, можно построить кривую ![]() , представляющую собою изменение интенсивности пучка лучей Ix в зависимости от глубины х проникновения лучей в поглощающее тело (рисунок 5.6,а). Эта зависимость получается более простой, если по оси абсцисс откладывать не
, представляющую собою изменение интенсивности пучка лучей Ix в зависимости от глубины х проникновения лучей в поглощающее тело (рисунок 5.6,а). Эта зависимость получается более простой, если по оси абсцисс откладывать не ![]() , а
, а ![]() , так как в этом случае получим прямую линию ( рисунок 5.1.6, б).
, так как в этом случае получим прямую линию ( рисунок 5.1.6, б).
В самом деле логарифмируя (5.22), имеем:
![]()
или
![]() , и
, и ![]() (5.23)
(5.23)
т.е. ![]() пропорционален глубине х проникновения лучей.
пропорционален глубине х проникновения лучей.
Наклон этой прямой дает меру коэффициента ослабления:
![]()
а) →![]() б) →
б) →![]()

Рисунок 5.6 - Кривые изменения интенсивности пучка однородных лучей в зависимости от глубины проникновения в поглощающее тело (абсорбционные кривые).
Определив таким образом μ и зная коэффициент рассеивания σ, можно найти коэффициент поглощения:
![]() .
.
На рисунке 5.6,б нанесены две пунктирные линии, из которых линия α отвечает лучам с большей длиной волны, коэффициент ослабления которых больше ![]() , и кривая b - более жесткими лучами, для которых
, и кривая b - более жесткими лучами, для которых ![]() и
и ![]() .
.
Эти кривые носят название абсорбционных кривых и качественно характеризуют проникающую способность лучей. Более наглядную характеристику проникающей способности лучей дает так называемый слой половинного ослабления, определяющей собой толщину Δ слоя обучаемого тела, при прохождении которого интенсивность пучка лучей ослабляется в два раза, т.е.
![]() .
.
Коэффициент ослабления μ связан с толщиной слоя половинного ослабления Δ , измеренной в сантиметрах, соотношением:
![]() , (5.23)
, (5.23)
которое легко получается из уравнения (5.21). Логарифмируя это уравнение и подставляя ![]() получим:
получим:
![]()
откуда
![]() .
.
Толщина Δ слоя половинного ослабления легко определяется из абсорбционных кривых. Так, для лучей трех различных длин волн, абсорбционные кривые которых показаны на рисунке 5.6,б, слои половинного ослабления будут 3, 4 и
 |
В и Е - кванты, которые прошли через тело пациента без взаимодействия; С и D — рассеянные кванты. квант D отсеивается сеткой, препятствующей рассеянному излучению, квант А поглощается в теле.
Рисунок 5.7 - Компоненты системы для получения рентгеновских изображений.
Кванты делятся на:
1. первичные В и Е, которые прошли через тело пациента, непровзаимодействовав с ним
2. вторичные Д и С, которые провзаимодействовали с телом, рассеялись и отклонились от направления первоначального распространения
Очевидно, что вторичные кванты С и Д не несут полезной информации и их надо как-то фильтровать. Для этого вводится устройство, называемое сеткой – свинцовые ячейки, на которых задерживаются рассеянные кванты. Первичные тоже задерживаются, но если не задерживать вторичные кванты, то получится серое изображение. Нас интересуют только первичные кванты, которые несут информацию о вероятности того, что квант проходит через тело пациента без взаимодействия.
Рассмотрим простую математическую модель процесса получения рентгенографического изображения, представленную на рисунке 5.7.
 |
Изображение регистрируется в плоскости XY.
N - число квантов, падающих на единицу площади пациента (должно быть минимальным) I(x,y)dxdy – энергия поглощаемая приемником площадью dxdy
Рисунок.5.8 - Простая модель получения рентгеновского изображения, показывающая распространение первичных и вторичных (рассеянных) квантов
Справедливо соотношение:

где Е – энергия кванта;
Iперв. кв. – интенсивность первичных квантов;
Iвтор. кв. – интенсивность вторичных квантов;
m(x,y,z) – линейный коэффициент ослабления излучения в тканях. ;
А1, А2 – точки входа и выхода излучения из тела пациента ;
x – коэффициент поглощения энергии прибора регистратором (зависит от Е и от угла прихода кванта q):
1. для первичных квантов угол равен нулю и энергия равна Е
2. для вторичных квантов угол произволен (q), энергия тоже меняется в некоторых пределах
S – функция, характеризующая рассеивающие свойства вещества ;
W – вариация угла рассеяния;
Функция рассеивания S зависит от распределения тканей и их положения в организме. Многочисленные экспериментальные исследования и теоретические расчеты позволили (для тела человека) установить следующее соотношение:
![]()
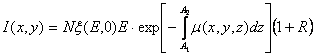 (5.10)
(5.10)
преобразование Радона
где,
R – отношение рассеянного излучения к первичному (эта константа определяется либо путем измерений, либо расчетным путем)
Следовательно, нужно использовать принцип полпрозрачности тканей. Если коэффициент прохождения ~ 1, то различие в проникающей способности через разные ткани будет малым, и контраст в изображении низким. На практике используют от 17 кэВ (при толщине ткани 1-
Фотоэлектрический эффект представляет собой такое взаимодействие квантов, при котором квант рентгеновского излучения поглощается тканью, при этом образуется фотоэлектрон и несколько характеристических рентгеновских квантов. В биоткани фотоэлектрон имеет энергию 150 кэВ и, следовательно, очень быстро поглощается (свободная длина пробега
Рассеянное излучение имеет более плавную характеристику от энергии, однако, при рассеянии образуются рентгеновские кванты, энергия которых лишь немного меньше энергии падающего излучения (падающее 25 кэВ – рассеянное 22,8 кэВ, падающее 100 кэВ – рассеянное 71,9 кэВ) и рассеянное излучение практически не поглощается тканью и доходит до приемника и эти кванты необходимо фильтровать.
На рисунке 5.10 приведены зависимости линейного коэффициента ослабления от энергии кванта, как для фотоэлектрического поглощения, так и для рассеяния. Последний вид взаимодействия не дает вклада в поглощение квантов. На рисунке 5.10 приведена также зависимость поглощенной компоненты излучения, обусловленной рассеянием и передачей энергии электронам отдачи. Видим, что при энергиях приблизительно до 25 кэВ для мягких тканей сечение фотоэлектрического процесса больше, чем сечение рассеяния.
 |
Рисунок 5.10 - Зависимость линейного коэффициента ослабления излучения от энергии кванта для мягких биотканей.
На рисунке 5.11 показаны зависимости линейных коэффициентов ослабления излучения костными и мягкими тканями от энергии. Различие между коэффициентами для этих тканей обусловлено главным образом разницей в сечениях фотоэффекта и плотностями биотканей и ясно показывает, почему рентгеновские лучи столь хорошо подходят для получения изображений переломов костей.
Различие на рисунке 5.11 между двумя кривыми и, следовательно, контраст в изображении костной и мягкой тканей уменьшаются с увеличением энергии квантов.
Главное условие: решение реконструкции томограммы представляет собой решение некорректной задачи, малые шума приводят к большим шумам в реконструированной томограмме. Так как не можем увеличивать лучевую нагрузку на человека, необходимо изучать контраст и нерезкость изображения.
 |
Рассмотрим простейшую модель объекта, представленную на рисунке 5.12
 |
С – контраст ,
I1 – энергия, поглощенная приемником за пределом мишени
I2 – энергия, поглощенная приемником после прохода через мишень
Рисунок 5.12 - Простая модель для оценки величины контраста.
Тело пациента заменяется однородным блоком ткани толщиной ![]() с линейным коэффициентом ослабления
с линейным коэффициентом ослабления ![]() . Внутрь этого блока помещается другой блок ткани (называемой "мишенью") толщиной
. Внутрь этого блока помещается другой блок ткани (называемой "мишенью") толщиной ![]() с линейным коэффициентом ослабления
с линейным коэффициентом ослабления ![]() . Ткань мишени – это тот объем, который необходимо визуализировать с большой четкостью в проекционной рентгенографии. Контраст
. Ткань мишени – это тот объем, который необходимо визуализировать с большой четкостью в проекционной рентгенографии. Контраст ![]() в изображении ткани мишени определяется с помощью функций распределения изображения
в изображении ткани мишени определяется с помощью функций распределения изображения ![]() и
и ![]() , которые дают энергию, поглощенную единицей площади поверхности приемника соответственно за пределами изображения ткани мишени и внутри него
, которые дают энергию, поглощенную единицей площади поверхности приемника соответственно за пределами изображения ткани мишени и внутри него
![]()
При использовании выражения (5.1) получаем:
![]()
где m2 , m1 – линейный коэффициенты поглощения.
Таким образом к факторам влияющим на контраст С изображения относятся толщина ткани мишени х и разность линейных коэффициентов поглощения (m2-m1), также отношение интенсивности рассеянного излучения к первичному R.
Нерезкость рентгенографической системы изображения важный фактор, определяющий процесс формирования изображения проекций, зависящий от конструктивных особенностей рентгеновской трубки, свойств приемника и движений пациента.
Контраст равнозначен глубине модуляции, а нерезкость – смазу передаточной функции изображения. Наиболее полно свойства рентгенографической системы определяются передаточной функцией системы. В настоящее время для каждой изображающей системы строится ее передаточная функция или кривая контраст-размер.
Наиболее общим методом определения процесса формирования изображения является измерение модуляционной передаточной функцией. Модуляционную передаточную функцию измеряют при помощи тест объекта в виде решетки.
На рисунке 5.13 приведены кривые зависимости контраста от энергии квантов для двух видов биотканей, представляющих особый интерес для маммографических исследований. Эти кривые показывают, что контраст резко уменьшается с увеличением энергии квантов, так что для получения большего контраста необходимо использовать излучение низкой энергии. Однако, как уже упоминалось выше, последнее требование влечет за собой высокую дозу облучения пациента, и поэтому должен быть найден компромисс между достаточным контрастом и наименьшей дозой облучения.
 |
Рисунок 5.13 - Изменение контраста с энергией для двух
наиболее важных для маммографии сред
Томография позволяет резко увеличить контраст изображения, из-за того, что через любую точку проходит много лучей под разными углами.
Простой расчет позволяет указать те ткани, которые можно различить с помощью обычной трансмиссионной рентгеновской аппаратуры. Коэффициенты линейного ослабления в воздухе, костной и мышечных тканях, а также в крови имеют соответственно следующие значения:

для типичного энергетического спектра излучения рентгеновских аппаратов. Ослабление первичного рентгеновского пучка слоем мягкой ткани с полостью внутри размером ![]() .
.
Обычные рентгеновские пленки позволяют визуально легко различить контраст порядка 2%, так что ребро толщиной
При регистрации рентгеновского изображения возникает шум, который обусловлен двумя факторами:
1.Флуктуация числа рентгеновских квантов, регистрируемых единицей площади приемника – квантовый шум.
2.Флуктуация сигнала, обусловленная характеристиками приемника и всей системы отображения.
Уровень квантового шума, который возникает при формировании проекции можно снизить за счет увеличения числа квантов регистрирующих приемников, однако, при этом увеличивается доза облучения пациента.
Возьмем модель, представленную на рисунке 5.14 и определим, какая должна быть доза на поверхности моделей, обеспечивающая контраст С на площади А относительно квантового шума, т.е. нужно оценить соотношение сигнал/шум.
 |
Рисунок 5.14 - Модель
Имеется сигнал ![]() , который мы пытаемся зарегистрировать,
, который мы пытаемся зарегистрировать,
где ![]() .
.
Таким образом,
![]()
Квантовый шум в изображении обусловлен флуктуациями энергии, поглощаемой в приемнике. Для простоты будем считать, что каждый фотон, взаимодействующий с детектором, полностью поглощается и что эффективность ![]() приемника одна и та же, как для первичных, так и вторичных квантов. Число квантов, регистрируемых единицей площади поверхности приемника, является пуассоновским процессом, а шум изображения на площади
приемника одна и та же, как для первичных, так и вторичных квантов. Число квантов, регистрируемых единицей площади поверхности приемника, является пуассоновским процессом, а шум изображения на площади ![]() , прилегающей к области "мишени", равен
, прилегающей к области "мишени", равен ![]() .
.
Если ![]() – сигнал,
– сигнал,![]() – шум,
– шум,![]() – отношение сигнал/шум, то можно записать следующие выражения:
– отношение сигнал/шум, то можно записать следующие выражения:
![]()
![]()
Если подставить ![]() , то
, то ![]() может быть записано в виде:
может быть записано в виде:
![]()
Экспериментальные исследования показали, что в рентгенографии объект можно зарегистрировать, когда шум превышает некоторый порог, который обозначается буквой «k» (экспериментально нашли, что k=5)
Если поставить k=5 можно определить N:
![]()
Если выбрать отношение k, то можно определить количество квантов N, которое необходимо, чтобы обеспечить данное отношение сигнал/шум.
Поверхностная доза облучения вычисляется как произведение числа квантов, приходящихся на единицу площади (в нашем случае это Ν) на массовый коэффициент поглощения энергии биотканью ![]() , и на энергию кванта (Е).
, и на энергию кванта (Е).

где ρ – плотность ткани;
ЕП – энергия поглощения.
Типичная схема получения данных в РТ при реконструировании изображений поперечных слоев дана на рисунке 5.15. Проводят большое количество измерений, каждое из которых соответствует определенному взаимному положению источника и детектора рентгеновского излучения. Источник и детектор находятся в плоскости сечения, изображение которого требуется получить. Для каждой комбинации положений источник — детектор выполняют два измерения — калибровочное и рабочее. Поясним это на примере одного определенного положения источника и детектора.
Когда проводят калибровочное измерение, то рентгеновское излучение от источника не проходит через объект, сечение которого необходимо получить. В действительности часть пучка, которая пересекает так называемую область реконструкции (рисунок 5.6.1), проходит через однородную среду эталонного вещества, например через воздух или воду. По калибровочному измерению можно судить о том, какая часть из большого, но определенного числа вышедших из источника фотонов регистрируется детектором. Эталонный детектор позволяет скомпенсировать вариации интенсивности источника рентгеновского излучения. С этой целью число фотонов, сосчитанных детектором, делят на число фотонов, зарегистрированных эталонным детектором. Во время проведения рабочих измерений исследуемый объект помещают в область реконструкции и (частично) замещают эталонное вещество. То, что исследуемый объект не должен занимать пространства вне поля реконструкций, является существенным ограничением. С другой стороны, дополнительные предметы могут занимать определенное положение вне области реконструкции, как при калибровке, так и при рабочем измерении. Примером является объект, который на рисунке 5.15 назван компенсатором и который компенсирует тонкие участки поперечных слоев тела человека вблизи границ сечений. Это делают для того, чтобы число фотонов, достигших детектора при различных положениях последнего, не отличалось столь сильно и тем самым чтобы диапазон скорости счета фотонов, при котором должен работать детектор рентгеновского излучения, был небольшим. Рабочее измерение проводят точно так же, как и калибровочное, с той лишь разницей, что сечение, изображение которого получают, теперь находится на пути рентгеновского излучения. Это изменяет число фотонов, сосчитанных детектором, но не изменяет числа фотонов, которое регистрируется эталонным детектором.

Рисунок 5.15 – Блок-схема съема данных в реконструктивной томографии
Таким образом, соотношение между рабочим и калибровочным измерениями зависит от поглощения способности исследуемого объекта и действия его как рассеивателя рентгеновского излучения относительно эталонного вещества.
Калибровочное и рабочее измерения производят для каждого из большого числа положений источник — детектор. По этим двум наборам чисел получают набор чисел Хаунсфилда, которые характеризуют сечение исследуемого объекта. В следующем разделе рассмотрим физическую сущность чисел Хаунсфилда и получаемых изображений.
В вакууме все фотоны рентгеновского излучения, которые вылетают из источника в направлении детектора, достигают последнего. Когда между источником и детектором помещено какое-нибудь вещество, некоторая часть фотонов, покидающих источник в направлении детектора, последнего не достигнет, так как они либо поглощаются, либо рассеиваются. Вероятность того, что фотон будет удален из первичного пучка, определяется энергией данного фотона и характеристиками вещества, которое находится между источником и детектором рентгеновского излучения.
Линейный коэффициент ослабления ![]() - ткани определяют следующим образом. Пусть p - вероятность того, что фотон с энергией
- ткани определяют следующим образом. Пусть p - вероятность того, что фотон с энергией ![]() , который входит в однородный слой ткани перпендикулярно поверхности данного слоя L, не поглотится и не рассеется в этом слое, т.е. p - степень пропускания данным слоем фотона с энергией
, который входит в однородный слой ткани перпендикулярно поверхности данного слоя L, не поглотится и не рассеется в этом слое, т.е. p - степень пропускания данным слоем фотона с энергией ![]() в направлении L. Определим
в направлении L. Определим
![]()
![]() (5.11)
(5.11)
где ln означает натуральный логарифм. Отметим, что величина линейного коэффициента ослабления зависит от используемых единиц длины. Линейный коэффициент ослабления рентгеновского излучения измеряют в единицах, обратных единице длины. Например, линейный коэффициент ослабления рентгеновского излучения с энергией 73 кэВ для воды равен 0,19 см-1.
В дальнейшем будем использовать так называемое относительное линейное ослабление рентгеновского излучения при энергии ![]() . Для любой точки пространства относительное линейное ослабление равно
. Для любой точки пространства относительное линейное ослабление равно ![]() , где t - ткань, которая находится в данной точке пространства во время рабочих измерений, и а - вещество, которое находится в этой же точке во время калибровочных измерений. Так как пространство за пределами поля реконструкции остается неизменным во время проведения рабочих и калибровочных измерений, то относительное линейное ослабление для всех точек, находящихся вне поля реконструкции, равно нулю для рентгеновского излучения с любой энергией. Заметим также, что для любой точки, которая находится внутри поля реконструкции, величина
, где t - ткань, которая находится в данной точке пространства во время рабочих измерений, и а - вещество, которое находится в этой же точке во время калибровочных измерений. Так как пространство за пределами поля реконструкции остается неизменным во время проведения рабочих и калибровочных измерений, то относительное линейное ослабление для всех точек, находящихся вне поля реконструкции, равно нулю для рентгеновского излучения с любой энергией. Заметим также, что для любой точки, которая находится внутри поля реконструкции, величина ![]() имеет одинаковое значение, так как можно считать, что эталонный материал является однородным и не изменяется во время калибровочных измерений.
имеет одинаковое значение, так как можно считать, что эталонный материал является однородным и не изменяется во время калибровочных измерений.
Теперь допустим, что нас интересует слой толщиной
Предположим для примера, что поле реконструкции, показанное на рис. 2.8, представляет собой квадрат 41,6 х
Требования к томографу:
1. Получать произвольно ориентированные сечения.
2. Обеспечивать нужную лучевую нагрузку.
3. Время измерений.
4. Достоверность получаемых результатов.
Схема томографа, представленная на рисунке 5.16 первого типа может быть построена с использованием:
1. одного источника.
2.
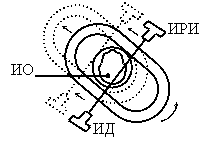 |
ИРИ – источник рентгеновского излучения.
ИД – информационный детектор.
ИО – исследуемый объект.
Рисунок 5.16
для получения изображения необходимо осуществить два вида движения: поступательное и вращательное. Рассмотренная модель достаточно проста и может быть отнесена к медленнодействующим.
Применение: исследование головы, нейрофизиология, нейрохирургия.
Схема томографа второго типа, представленная на рисунке 5.17, имеет время измерения tизм=2c.
Используются несколько приемников, соединенных в блок. При увеличении шага по углу, число поворотов уменьшается. Применяются поступательное и вращательное движение.
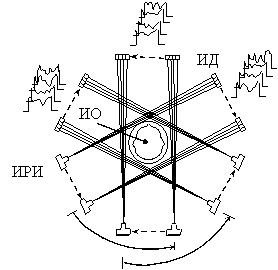 |
Рисунок 5.17
Достоинства: получение высокой пространственной разрешающей способности при приемлемом времени сбора данных и восстановления изображения.
Недостатки: сложности, связанные с приемом и предварительной обработки информации.
 |
Рисунок 5.18
Достоинства: исключение двух видов движения элементов сканирующего устройства (осуществляется лишь вращательное движение). Малое время сканирования за счет непрерывного вращательного движения.
Недостатки: существует необходимость создания высокоточной механической конструкции, обеспечивающей минимальное биение на оси подшипника.
Необходимость формирования веерного рентгеновского пучка с высокими показателями по равномерности. Необходимость создания стабильной линейки идентичных детекторов с высоким КПД. Необходимы вычислительные средства для обработки данных с высокой производительностью и в реальном времени.
Необходимы новая формула обращения, новые алгоритмы и конструкции.
Схема томографа четвертого типа представлена на рисунке 5.19
 |
Рисунок 5.19
Недостатки: Сложности с построением круговой детектирующей системы, с высокими характеристиками.
 |
Схема томографа пятого типа представлена на рисунке 5.20
Рисунок 5.20
Состоит из круговой линейки детекторов и группы источников рентгеновского излучения.
Первой идею спирального сканирования запатентовала японская фирма TOSHIBA в 1986 году. T. Katakura с соавторами выполнили первое клиническое исследование на спиральном КТ в 1989 году.
Внедрение в 1989 году в медицинскую практику новой методики КТ-спиральной томографии явилось крупнейшим достижением за 20 лет ее существования, открыло принципиально новые возможности в диагностике целого ряда патологических состояний. Как известно, в обычной КТ однократное сканирование дает изображение одного слоя, соответственно, цикл сканирования повторяется после очередного перемещения стола столько раз, сколько послойных изображений нужно получить. В спиральной томографии осуществляется непрерывное движение трубки вокруг исследуемой зоны при параллельном равномерном продвижении стола с пациентом в продольном направлении. Траектория движения рентгеновской трубки к продольной оси исследуемого объекта приобретает форму спирали, что и дало название методу (рисунок 5.21).
|
|
| а) - Схема обследования пациента на классических КТ. Рисунок 5.21 |
В отличие от обычной КТ при спиральном сканировании конечная точка среза не совпадает с исходной из-за перемещения объекта во время сканирования.
Быстрая ротация излучающей трубки в спиральных томографах, отсутствие интервалов между циклами излучения для продвижения стола в следующую позицию значительно сокращают время исследования. Это приводит к повышению пропускной способности кабинета, облегчает исследование больных, которые не могут длительно задерживать дыхание, долго находиться в аппарате (травматические, больные дети, пациенты в тяжелом состоянии).
Высокая скорость сканирования позволяет получать значительно более четкие изображения с меньшими артефактами от физиологических движений. Новая технология улучшила также качество изображений движущихся органов грудной клетки, брюшной полости.
Снижение времени облучения делает метод КТ более безопасным для пациентов.
К преимуществам спиральной КТ необходимо отнести возможность реконструкции изображения в любой заданной плоскости. При спиральной томографии получаемые данные извлекаются из всего сканируемого объекта, что позволяет получать изображение любого зафиксированного слоя из отсканированного объема.
Томограф 6-ого поколения использует трубу детектора и конический пучок.
В таблице 5.3 приведены характеристики томографов в зависимости от поколения.
Таблица 5.3
| Поколение |
Характеристика |
Кол-во источников |
Кол-во приемников |
Время сканирования одного слоя. |
Время сканирования слоев 3-х мерного объекта |
Примечание |
| Первое |
Один пучок |
1 |
1 |
2мин |
- |
Применяется в промыш. томографии и нейрохирургии |
| Второе |
Многократный луч, небольшой угол раствора , веерный пучок. |
1 |
8-30 |
20 с. |
- |
Применяется ограниченно |
| Третье |
Широкий угол раствора, веерный пучок, вращат. движение |
1 |
500 |
2 с. |
~1 мин. |
Широко применяется |
| Четвертое |
Широкий угол раствора, веерный пучок, вращат. движение |
1 |
1000 |
2 с. |
~1 мин. |
Широко применяется |
| Пятое |
Многократный источник веерного пучка с меньшим механическим вращением |
5…20 |
500 |
0.4 с. –0.1 с. |
~20 сек. |
Ограниченно из-за высокой стоимости |
| Шестое |
Многократный источник двухконусная геометрия, конусная геометрия |
200 |
5000 |
- |
20 мс |
Исследование инфаркта миокарда |
При прохождении через тело рентгеновского излучения ослабление последнего в каждой точке определяется материалом, находящимся в этой точке, и энергетическим спектром рентгеновского излучения. Спектр рентгеновского излучения, которое используют для РТ, состоит из большого числа энергетических уровней, т.е. является полихроматическим, и по мере прохождения через объект излучение становится более жестким. Поэтому ослабление в определенной точке может меняться в зависимости от направления прохождения пучка рентгеновского излучения через эту точку. Если бы спектр используемого рентгеновского излучения содержал только один энергетический уровень, т.е. излучение было бы монохроматичным, то все обстояло бы иначе: каждая точка имела бы однозначное определенное значение коэффициента ослабления и реконструкция этого распределения коэффициентов представляла бы достаточно хорошо определенную задачу реконструктивной томографии.
Желательным для медицинской диагностики является следующее утверждение: число Хаунсфилда, соответствующее определенному элобу, задается свойствами ткани, которая находится в данном злобе, и не зависит от местоположения данного элоба в слое. Как будет видно из дальнейшего, именно это утверждение предполагается при построении математических действий для вычисления чисел Хаунсфилда.
Правильным является также определение числа Хаунсфилда, при котором оно кратно среднему относительному ослаблению элоба при заданной энергии е рентгеновского излучения. Предположим теперь, что источник дает монохроматическое рентгеновское излучение с энергией фотонов ![]() . Пусть для некоторого фиксированного положения пары источник — детектор результат калибровочного измерения (т.е. количество сосчитанных фотонов, доходящих от источника до детектора в опыте, когда между ними не находится исследуемый объект, деленное на количество фотонов, сосчитанных эталонным детектором) равен Ст. Пусть Ат — результат рабочего измерения (т.е. количество фотонов, которые доходят от источника до детектора в опыте, когда между ними находится исследуемый объект, деленное на количество фотонов, сосчитанных эталонным детектором). Определим монохроматическую лучевую сумму т для этого пучка рентгеновского излучения по формуле 5.12.
. Пусть для некоторого фиксированного положения пары источник — детектор результат калибровочного измерения (т.е. количество сосчитанных фотонов, доходящих от источника до детектора в опыте, когда между ними не находится исследуемый объект, деленное на количество фотонов, сосчитанных эталонным детектором) равен Ст. Пусть Ат — результат рабочего измерения (т.е. количество фотонов, которые доходят от источника до детектора в опыте, когда между ними находится исследуемый объект, деленное на количество фотонов, сосчитанных эталонным детектором). Определим монохроматическую лучевую сумму т для этого пучка рентгеновского излучения по формуле 5.12.
![]() (5.12)
(5.12)
Назовем множество т для всех положений пары источник - детектор монохроматическими проекционными данными. Основываясь на физических и математических фактах, которые были рассмотрены выше, можно утверждать, что относительное линейное ослабление в слое при определенной энергии рентгеновского излучения е можно точно оценить по монохроматическим проекционным данным.
В реальных условиях пучок рентгеновского излучения полихроматичен. Пусть С и А - результаты калибровочного и рабочего измерений соответственно для определенного положения пары источник — детектор при полихроматическом пучке рентгеновского излучения. Определим полихроматическую лучевую сумму для данного пучка рентгеновского излучения следующим образом:
![]() (5.13)
(5.13)
и назовем набор всех возможных р для всех возможных положений пары источник - детектор полихроматичными проекционными данными.
Нашу проблему можно сформулировать так. Для любого положения пары источник - детектор можно измерить полихроматическую лучевую сумму p, а для процесса реконструкции требуется монохроматическая лучевая сумма w. Естественно встает вопрос: определяет ли величина p величину m ? К сожалению, за исключением частных случаев, не имеющих практического интереса, ответ на этот вопрос отрицательный.
Более прагматичным является вопрос: можно ли по данному значению p достаточно хорошо аппроксимировать т, так, чтобы получить необходимые для диагностики числа Хаунсфилда? По-видимому, ответ на этот вопрос должен быть утвердительным, как это иллюстрирует материал, приведенный ниже.
Принципиальные ограничения точности измерений, которые проводятся в РТ, определяются статистической природой процессов излучения фотонов рентгеновского излучения, взаимодействия Их с веществом и детектирования. Обсудим последовательно каждый из этих процессов.
Рассмотрим эксперимент, в котором регистрируют все фотоны, которые испускает стабильный источник рентгеновского излучения в направлении детектора за единицу времени. Подобный эксперимент приводит нас к дискретной случайной переменной, которая была обозначена Y. Возможные исходы такого эксперимента представляют собой неотрицательные целые числа, равные числу фотонов. Без каких-либо физических доказательств примем, что существует определенное вещественное число X, такое, что
![]() (5.14)
(5.14)
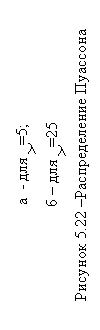
Символ ехр означает экспоненциальную функцию; и поэтому ехр[ln(x)] = ln{exp(x)] = х. На рисунке 5.22 приведены графики PY(y) для у = 0, . . . , 45 при l = 5 и l= 25. Выражение (5.14) называют законом распределения вероятности Пуассона, а случайную переменную Y, которая удовлетворяет этому закону, называют случайной переменной Пуассона с параметром л . Отметим здесь три важных свойства такой случайной переменной:
а) ее среднее значение (математическое ожидание) равно l;
б) ее стандартное отклонение равно l1/2;
в) при значениях l > 100 случайная переменная дает нормальное распределение.
Эти свойства имеют важное практическое значение. Пусть, например, нас интересует оценка среднего числа фотонов X, испущенных за единицу времени стабильным источником рентгеновского излучения в направлении детектора. Если имеется система счета всех фотонов, достигающих детектора, то можно оценить l, сосчитав количество фотонов за определенный отрезок времени, т.е. получив выборку случайной величины. Если l= 10 000, то тогда имеется приблизительно один шанс из 20, что ошибка равна двум стандартным отклонениям (200) или больше. Другой способ состоит в том, что мы считаем, число фотонов за 100 таких единиц времени и делим полученное количество на 100, чтобы получить оценку l. Общее число фотонов за этот более длительный период времени равно в среднем для нашего примера 1 000 000, и в 19 случаях из 20 полученные значения сосчитанных фотонов в одной какой-либо выборке, оценка будет находиться в пределах 9980 — 10 020, т.е. погрешность равна 20 или меньше. Увеличив время измерения фотонов в 100 раз, мы уменьшаем величину вероятной погрешности в наших оценках в 10 раз. Подобное же явление наблюдаем в других случаях всегда, когда рассматриваем вопрос о том, каким образом точность калибровочных и рабочих измерений зависит от общего числа зарегистрированных фотонов.

Теперь рассмотрим вопросы, связанные со статистической природой взаимодействия фотонов рентгеновского излучения с веществом. Пусть фотоны вылетают из источника в направлении детектора по прямой L. Тогда имеется определенная вероятность p того, что какой-то определенный фотон долетит до детектора и не будет ни рассеян, ни поглощен. Эта вероятность зависит от энергии данного фотона и характеристик вещества, находящегося между источником и детектором, которое пересекает фотон по прямой L. Назовем величину p пропусканием данного вещества вдоль прямой L рентгеновского излучения с определенной энергией. Если все остается без изменений в пространстве между источником и детектором в течение определенного периода времени и в течение этого периода 10 000 фотонов одной и той же энергии вылетают в направлении детектора по прямой L, то число фотонов, достигающих детектора, приблизительно равно 10000р. Остальные фотоны либо рассеются, либо поглотятся.
Какой-то фотон, достигший детектора, не обязательно будет им зарегистрирован. Для каждого определенного фотона имеется определенная вероятность, а того, что этот фотон, достигнув детектор, будет сосчитан последним. Назовем эту величину, а эффективностью детектора для фотонов рентгеновского излучения с данной энергией. Обобщая случай, рассмотренный выше, мы находим, что число фотонов из 10 000 вылетевших из источника в указанном направлении, которые не поглотятся, не рассеются и будут сосчитаны детектором, равно примерно 10 000 ps.
Пусть l— среднее число фотонов с энергией ![]() , которые испускает за единицу времени стабильный источник рентгеновского излучения по прямой L в направлении детектора. В этом случае p — пропускание вдоль прямой L для данного вещества рентгеновского излучения с энергией е, а s — эффективность детектора для рентгеновского излучения с данной энергией
, которые испускает за единицу времени стабильный источник рентгеновского излучения по прямой L в направлении детектора. В этом случае p — пропускание вдоль прямой L для данного вещества рентгеновского излучения с энергией е, а s — эффективность детектора для рентгеновского излучения с данной энергией ![]() . Тогда количество фотонов, которые имеют энергию
. Тогда количество фотонов, которые имеют энергию ![]() , достигают детектора без поглощения или рассеяния и регистрируются детектором за единицу времени, представляет собой отсчет случайной переменной Пуассона с параметром lps.
, достигают детектора без поглощения или рассеяния и регистрируются детектором за единицу времени, представляет собой отсчет случайной переменной Пуассона с параметром lps.
Теперь мы можем обсудить вопрос о том, что же измеряют на стадии сбора данных в РТ. Для этого предположим, что используемое рентгеновское излучение монохроматично и можно пренебречь собственными размерами источника и детектора рентгеновского излучения. Из последнего предположения следует, что все фотоны проходят от источника до детектора по одной и той же прямой и что, если какой-то фотон испытывает на этом пути рассеяние, он не попадает в детектор. В следующих разделах мы обсудим ошибки, которые вносятся вследствие того, что такие условия не выполняются на практике.
Пусть монохроматический пучок рентгеновского излучения с энергией е обладает тем свойством, что доля фотонов, которые испускаются в направлении эталонного детектора, равна fr, а доля фотонов, которые испускаются в направлении рабочего детектора, равна fd. Допустим, что средние значения числа фотонов, испускаемых за время калибровки и рабочих измерений, равны lс и lа соответственно. Пусть pr равно коэффициенту пропускания материала для фотонов с энергией ![]() , когда материал находится между источником и эталонным детектором, а pс и pа — коэффициентам пропускания для той же энергии рентгеновского излучения вещества, которое находится между источником и рабочим детектором при калибровке и в рабочих измерениях соответственно. Пусть sr и sd — значения эффективностей эталонного и рабочего детекторов соответственно для рентгеновского излучения с энергией
, когда материал находится между источником и эталонным детектором, а pс и pа — коэффициентам пропускания для той же энергии рентгеновского излучения вещества, которое находится между источником и рабочим детектором при калибровке и в рабочих измерениях соответственно. Пусть sr и sd — значения эффективностей эталонного и рабочего детекторов соответственно для рентгеновского излучения с энергией ![]() . Из только что приведенных рассуждений следует, что число фотонов, сосчитанных эталонным • и рабочим детекторами во время проведения калибровочных измерений, является отсчетом случайной переменной Пуассона со средними значениями frlcprsr и fdlcpcsd соответственно. Отсюда
. Из только что приведенных рассуждений следует, что число фотонов, сосчитанных эталонным • и рабочим детекторами во время проведения калибровочных измерений, является отсчетом случайной переменной Пуассона со средними значениями frlcprsr и fdlcpcsd соответственно. Отсюда
![]() (5.15 )
(5.15 )
Аналогично число фотонов, сосчитанных эталонным и рабочим детекторами за время проведения рабочих измерений, является отсчетом случайной переменной Пуассона со средними значениями frlaprsr и fdlapasd соответственно. Отсюда имеем
![]() (5.16)
(5.16)
Комбинируя (5.15) и (5.16), получаем
![]() (5.17)
(5.17)
 (5.18)
(5.18)
Именно поэтому монохроматическую лучевую сумму т можно использовать как оценку интеграла  в алгоритме вычисления в
в алгоритме вычисления в ![]() отдельных точках по значениям линейных интегралов от m(х, у) .
отдельных точках по значениям линейных интегралов от m(х, у) .
Важным является следующий вопрос: насколько точно величина т оценивает
-ln(pа/pс). В предположениях, сделанных выше, т является выборкой случайной переменной величины М, такой, что
![]() , (5.19)
, (5.19)
и
![]() , (5.20)
, (5.20)
где
![]() . (5.21)
. (5.21)
Если эту величину S можно сделать очень малой, то тем самым т дает точную оценку - ln(pа/pс).
Отметим, что один из способов сделать величину S малой заключается в том, чтобы число фотонов, вылетающих из источника (lс и la), было большим. Если исключить проблему перегрузок детекторов, то нет ограничений сделать lс достаточно большим и тем самым сделать пренебрежимо малыми два первых члена в выражении для S. В этом случае видно, что величина S обратно пропорциональна величине lа. К сожалению, число фотонов, покидающих источник во время проведения рабочих измерений, нельзя сделать произвольно большим, так как это приводит к недопустимо большой дозе облучения пациента и может замедлить процесс снятия проекций; поэтому погрешности, связанные с перемещениями, станут весьма существенными. Однако отметим, что если пропускание рг вещества, находящегося между источником и эталонным детектором, будет относительно большим (около 1), то последний член в выражении (5.21) становится пренебрежимо малым. Это приводит к выражению
![]() (5.22)
(5.22)
которое, в частности, показывает, что погрешность в оценке –ln(pa/pc) зависит от пропускания pа во время проведения рабочих измерений, а именно уменьшение пропускания ведет к увеличению погрешностей.
Как видно из сказанного выше, погрешности измерения, обусловленные статистической природой процессов излучения, фотонов рентгеновского излучения, их взаимодействия с веществом и их детектирования, являются неизбежными. Особенность этих погрешностей связана со случайным характером переменных. Как будет показано ниже, в некоторых алгоритмах реконструкции делают попытки использовать данные особенности. Так как эти погрешности влияют на конечные результаты, получаемые в процессе реконструкции, то важно знать как природу этих погрешностей, так и механизм влияния погрешностей на результаты, к которым приводит данный алгоритм реконструкции.
Пучок рентгеновского излучения, который используется для РТ, состоит из фотонов различных энергий. Такое излучение называют полихрома-тичным. Так как ослабление в определенной точке пространства обычно больше у фотонов с меньшей энергией, спектр распределения энергии пучка рентгеновского излучения изменяется и становится более жестким по мере прохождения через объект. Пучки рентгеновского излучения, приходящие в определенную точку внутри тела по разным направлениям, имеют, очевидно, разный энергетический спектр излучения, так как они проходят через различные ткани, прежде чем попадут в эту точку, и поэтому будут по-разному ослаблены в данной точке. Этот факт создает трудность, когда используют только одну величину для описания коэффициента ослабления рентгеновского излучения в данной точке тела.
Возможный выход из положения состоит в том, чтобы приписать данной точке коэффициент ослабления фотонов для определенной энергии. Если бы использовался пучок излучения, состоящего из фотонов только одной энергии, т.е. излучение было монохроматическим, то пучки, приходящие из разных направлений, были бы ослаблены в данной точке в одинаковой степени. Реконструкция по таким коэффициентам ослабления представляет собой достаточно хорошо определенную задачу реконструктивной томографии.
В данном разделе обсудим математические соотношения, которые описывают основные свойства полихроматических лучевых сумм, а также методы, используемые для оценивания соответствующих монохроматических лучевых сумм.
В полихроматическая лучевая сумма р аппроксимируется интегралом вида
 (5.23)
(5.23)
Приведем теперь более подробное объяснение использованных обозначений в выражении (5.23).
Пусть источник испускает полихроматический пучок рентгеновского излучения с энергией фотонов в пределах 0 - Е. Обозначим через τе вероятность того, что какой-то фотон, зарегистрированный во время проведения калибровочных измерений, имеет энергию е. Здесь мы используем отчасти нестандартное обозначение, используя те для обозначения функции энергии при значении е. Эту функцию назовем детектируемым спектром в калибровочных измерениях.
Величина He(z) является функцией двух переменных - энергии и расстояния z, и ее значения равны линейному коэффициенту ослабления излучения с энергией е в точке z на прямой L при проведении рабочих измерений. С другой стороны, величина ![]() является функцией только одной переменной - энергии е, и ее значение равно линейному ослаблению эталонного материала а при энергии е. Таким образом, выражение
является функцией только одной переменной - энергии е, и ее значение равно линейному ослаблению эталонного материала а при энергии е. Таким образом, выражение  является интегралом относительно линейного ослабления при энергии е вдоль прямой L.
является интегралом относительно линейного ослабления при энергии е вдоль прямой L.
Отметим, в частности, что полихроматическая лучевая сумма зависит только от относительных линейных ослаблений при всех значениях энергии в пределах 0 - E и от регистрируемого спектра излучения при калибровочных измерениях.
Тогда
 (5.23)
(5.23)
Напомним теперь, что числа Хаунсфилда кратны относительным линейным ослаблениям при определенной энергии е; их получают по оценкам монохроматических проекционных данных, которые сами вычисляются из полихроматических проекционных данных, получаемых экспериментально. Способ оценки монохроматических проекционных данных из полихроматических описан в остальной части этого раздела.
Начнем с теоретического рассмотрения одного частного случая. Пусть в течение рабочих измерений в области реконструкции имеется только два вида вещества а и b, причем а - эталонный материал. Рассмотрим какое-то определенное положение пары источник - детектор и предположим, что полная длина прямой L, которая проходит через материал , равна B2. Из выражений (5.10.10) и (3.10.11) имеем
 (5.26)
(5.26)
и
![]() . (5.26)
. (5.26)
Комбинируя выражения (5.25) и (5.26), получим
 . (5.27)
. (5.27)
Важным свойством выражения (3.10.14) является следующее: для всех значений энергии в пределах 0 — Е выполняется неравенство ![]() >
> ![]() либо
либо ![]() <
< ![]() причем правая часть выражения (5.23) является монотонно возрастающей функцией от 0 — Е, а tе положительно для всех значений е. Отсюда следует, что для любого данного значения р имеется только одно значение т, при котором правая часть выражения (5.27) равна его левой части. На практике при корректировке по спектру используют табулированное значение левой части формулы (5.27) и находят то значение т, для которого правая часть совпадает с экспериментально измеренной полихроматической лучевой суммой p.
причем правая часть выражения (5.23) является монотонно возрастающей функцией от 0 — Е, а tе положительно для всех значений е. Отсюда следует, что для любого данного значения р имеется только одно значение т, при котором правая часть выражения (5.27) равна его левой части. На практике при корректировке по спектру используют табулированное значение левой части формулы (5.27) и находят то значение т, для которого правая часть совпадает с экспериментально измеренной полихроматической лучевой суммой p.
Выражение (5.27) получено при весьма существенных ограничениях, когда имелись только два вида материала в области реконструкции. В тех случаях, когда проводится исследование области головы пациента, окруженной водяной баней, это предположение до некоторой степени оправданно. Голова состоит из костной ткани и из веществ, которые по своим свойствам ослабления рентгеновского излучения не слишком отличаются от свойств водяной бани. Поэтому в данном случае выражение (5.27) можно использовать для введения поправки на изменение спектра рентгеновского излучения, однако в общем случае оно хуже подходит для данных целей, чем другие способы, которые будут рассмотрены ниже.
Несмотря на то что метод, основанный на выражении (5.27), не является достаточно точным и надежным из-за существенных ограничений, лежащих в его основе, общий подход, который используют здесь, является достаточно привлекательным, так как позволяет задать такую функцию f(p) полихроматической лучевой суммы p, что если ее использовать для оценки монохроматической лучевой суммы т, то получим достаточно хорошие реконструкции относительных линейных ослаблений при фиксированном значении энергии е.
Естественными кандидатами для такой функции являются полиномы, т.е функция вида
![]() (5.28)
(5.28)
где n - порядок полинома - фиксированное целое число, a0, a1, . . ., an-1,
an – фиксированные коэффициенты, которые требуется определить так, чтобы f(p) давала приемлемую для наших целей оценку .
С точки зрения вычисления аппроксимация с помощью полиномов имеет два достоинства по сравнению, например, с аппроксимацией системой экспонент. Коэффициенты полинома достаточно легко вычислить, и, как только они получены, легко оценить также f(p). При этом обычно достаточно использовать небольшое число n, например n < 5 .
В некоторых случаях не существует единственной функции f(p), такой, что бы приводила к приемлемому восстановлению. В таких случаях приходится либо использовать несколько корректирующих функций, заданных для определенных положений пар источник - детектор, либо коррекции проводить итерационно, беря в качестве скорректированной функции данной итерации ту, которая соответствует восстановленным данным предыдущей итерации.
Пусть есть объект, и мы его освещаем, излучение, проходящее через объект, ослабевает. Затем мы объект поворачиваем и опять облучаем, излучение ослабевает, но элемент объекта освещается разными излучениями.
Описанные выше действия представены на рисунке 5.23.
 |
Рисунок 5.23.
Характеристики элемента будут давать разный вклад в проекцию и появляется погрешность проекционных данных, из-за чего возникают артефакты. Полихроматические артефакты вызваны тем, что томография оперирует изображениями, полученными под разными ракурсами.
Реальный источник имеет немонохроматическое излучение, а некоторый спектр. Когда излучение распределяется через объект, то спектр меняется. Более мягкое поглощается более жестко остается.
Полихроматический артефакт вызван функцией получения данных.
Методы борьбы с артефактами заключаются в следующем:
1. Делать излучение монохроматическим
2. Делать предварительное ужесточение луча
3. Принципиальное решение дает метод 2-х экспозиций.
Он состоит в том, что линейный коэффициент поглощения, оказывается, зависим от энергии
![]()
где,
1-ое слагаемое описывает фотоэлектрическое поглощение излучения с энергией Е, 2-ое – комптоновское рассеяние (s(E)-известна), тогда проекционные данные
![]()
![]()
где,
dS – элемент длины.
Если имеем ![]()
![]() ,
,
следовательно ![]() .
.
Поэтому восстановление сводится к определению чисел А1 и А2 ,которые не зависят от энергии, следовательно q1, q2 и m не будут иметь артефактов.
Значения А1 и А2 получают при измерении интенсивности излучения прошедшего через объект для 2-х различных спектральных зон.
S1(E) и S2(E), которые получаются различными способами: либо измерением анодных напряжений на трубке, либо использованием двух приемников с различными фильтрами. S1 и S2 выбирают такими , чтобы имела решение следующая система:


Решая эту системы, определим А1 и А2 , а затем m. Полихроматические артефакты удалось избежать за счет увеличения лучевой нагрузки.
Когда строят алгоритм реконструкции, то необходимо знать величины т(l,q} или линейный интеграл ![]() вдоль L для определенных l иq , т.е. для определенных прямых L. Статистика фотонов и изменение энергетического спектра рентгеновского излучения при прохождении через вещество являются причинами того, что физические измерения дают нам возможность только приближенно оценить значения т(l,q}. В этом разделе кратко обсуждаются источники других погрешностей.
вдоль L для определенных l иq , т.е. для определенных прямых L. Статистика фотонов и изменение энергетического спектра рентгеновского излучения при прохождении через вещество являются причинами того, что физические измерения дают нам возможность только приближенно оценить значения т(l,q}. В этом разделе кратко обсуждаются источники других погрешностей.
Одна из погрешностей связана с тем, что источник (фокальное пятно) рентгеновского излучения и детектор излучения имеют конечные размеры. Поэтому не все фотоны, которые регистрируются детектором, идут по одной и той же прямой от источника до детектора и фактически проходят по прямым, образующим пучок довольно сложной формы.

Рисунок 5.24 - Иллюстрация, поясняющая эффект частично заполненного объема
Так как фокальное пятно источника излучения и детектор имеют конечные размеры и этими размерами нельзя пренебречь, то возникает так называемый эффект частично заполненного объема, который поясним, рассмотрев упрощенный двумерный случай. Пусть имеется точечный источник монохроматического рентгеновского излучения Р и детектор D в виде отрезка линии (рисунок 5.24), и пусть линейный коэффициент ослабления равен нулю во всей области, кроме части области А, которая заштрихована на рисунке 5.24, где он равен 2. Примем, что длина заключенного между ad и bс отрезка любой из прямых, идущих от Р к D, равна 1. Допустим, кроме того, что эталонный материал, имеет линейный коэффициент ослабления, равный нулю (вакуум), и что число фотонов, регистрируемых эталонным детектором за время как калибровочного, так и рабочего измерения, равно 1000. Следовательно, число фотонов, вылетающих из источника е направлении детектора за время проведения калибровки, и соответствующее число фотонов за время проведения рабочего измерения приблизительно равны. Пусть это число составляет 1000000, Таким образом, в результате калибровочного измерения получим Ст ~ 1000. Если разбить пучок рентгеновского излучения на две равные половины, как показано на рисунке 5.24, то, очевидно, в каждую из половин А войдут примерно по 500000 фотонов. Из левой части, где линейный коэффициент ослабления равен 0 и, следовательно, пропускание равно 1, все 500000 фотонов дойдут до детектора. Из правой же части, где линейный коэффициент ослабления равен 2 и, следовательно, пропускание составит е-2 ~ 0,135, число фотонов, которые дойдут до детектора, будет равно примерно 68000. Следовательно, общее число зарегистрированных фотонов составит около 568000, и в результате рабочих измерений получим Ат @ 568 и имеем т @ 0,566. Это служит оценкой среднего значения линейного интеграла относительного линейного ослабления между источником и точками на детекторе. Однако легко видеть, что истинная величина этого среднего значения равна 1,0. Причина достаточно большой погрешности (43,4%) в оценке среднего значения в том, что лишь часть пучка рентгеновского излучения проходит через ослабляющую среду, а последующая математическая обработка результатов измерения, процедуры вычисления экспонент и логарифмов приводит к непропорционально большому весу измерений, обусловленных той частью пучка, которая проходит через пустую область.
В принципе можно уменьшить размеры источника и детектора, экранируя их фильтрами из свинца, и оставить очень узкие отверстия непосредственно перед ними, но это приводит к двум нежелательным последствиям. Во-первых, погрешность, связанная со статистикой, будет существенно увеличена, так как доля фотонов fd в выражении (5.22) очень мала. Во-вторых, нежелательный факт будет иметь место в тех случаях, когда методом томографии необходимо получить информацию о небольших по размерам деталях при исследовании больших по размерам органов, например опухолей в легких. Если слои очень тонкие, то для уверенности, что мы не пропустим то, ради чего ведем исследования, требуется большое число слоев. Это увеличивает машинное время обработки и, вероятно, загруженность специалиста по радиологии, который должен изучать томограммы каждого из этих слоев.
Здесь упомянуто лишь одно явление, которое типично для РТ. Способы, которые используют для подавления погрешностей, определяемых только физическими явлениями, приводят к увеличению погрешностей, связанных с другими явлениями.
Еще одним примером является способ подавления артефактов, обусловленных движением.
Важным предположением, лежащим в основе РТ, является то, что величины т(1, q), которые требуется измерить, представляют собой интегралы вдоль различных прямых одной и той же функции ![]() . Однако это предположение нарушается, если различные прямые L проходят через движущиеся органы, например сердце или легкие, и если рабочие измерения проводят в различные моменты времени для разных L. Поэтому функция
. Однако это предположение нарушается, если различные прямые L проходят через движущиеся органы, например сердце или легкие, и если рабочие измерения проводят в различные моменты времени для разных L. Поэтому функция ![]() претерпевает изменения по мере движения органов. Один из методов борьбы с этим заключается в использовании нескольких детекторов и, если можно, даже нескольких источников так, чтобы все измерения провести за такой малый промежуток времени, в течение которого орган сместится незначительно. Однако это приводит к увеличению погрешности, связанной с детектированием рассеянных фотонов, - явления, которое мы сейчас рассмотрим.
претерпевает изменения по мере движения органов. Один из методов борьбы с этим заключается в использовании нескольких детекторов и, если можно, даже нескольких источников так, чтобы все измерения провести за такой малый промежуток времени, в течение которого орган сместится незначительно. Однако это приводит к увеличению погрешности, связанной с детектированием рассеянных фотонов, - явления, которое мы сейчас рассмотрим.
Отметим, что определенный детектор регистрирует только те фотоны, которые покидают источник в направлении этого детектора и достигают его, не участвуя в процессах поглощения или рассеяния. Если рассматривается только одна пара источник - детектор, то такое предположение верно, так как рассеянный фотон может прийти в данный детектор только в том случае, если он был рассеян на очень малый угол относительно своего первоначального направления или если он был многократно рассеян таким образом, что, в конце концов, попал в данный детектор. Последние случаи маловероятны, поэтому погрешность, связанная с рассеянием в случае одной-единственной пары источник - детектор, крайне мала. Однако, когда имеется несколько детекторов, фотон, первоначально шедший в направлении определенного детектора, может сравнительно легко рассеяться так, что попадает в другой детектор и будет сосчитан последним. Так как отношение рассеянных фотонов к нерассеянным, которые попадают в данный детектор, зависит от типа объекта, изображение которого реконструируется достаточно сложным образом, погрешность, вносимую рассеянием, нельзя полностью устранить из измерений до стадии реконструкции. Коллиматор, который поглощает фотоны, идущие в детектор с направлений, отличных от направления на источник, может уменьшить число рассеянных фотонов, зарегистрированных данным детектором.
Наконец, рассмотрим погрешности, которые возникают из-за аппаратуры, используемой при регистрации экспериментальных данных для РТ. Важно, чтобы источник и детектор не изменяли своих характеристик во время проведения калибровочных и рабочих измерений. Например, мы предполагали, что эффективность ad не изменяется во время проведения калибровочных и рабочих измерений. Изменение эффективности детектора приведет к тому, что выражение (5.17) станет неверным.
Эффективность детектора предполагается не зависящей от количества фотонов, которые требуется сосчитать данным детектором. Однако на практике этого часто бывает трудно достигнуть, так как детектор может выйти в состояние насыщения, если на него поступает слишком много фотонов. Один из способов борьбы с таким явлением заключается в использовании компенсатора, благодаря которому полное ослабление оказывается большим, и насыщение детектора исчезает для фотонов, которые либо проходят мимо объекта, либо его слегка касаются. Иначе этого можно достигнуть, если в качестве эталонной среды взять воду, окружая ею объект исследований во время проведения рабочих измерений. Первый метод предпочтителен, потому что он требует меньшую дозу облучения для набора одинаковой статистики фотонов, так как фотоны поглощаются водой, которая находится между телом пациента и детектором.
Важной также является механическая стабильность; направления, по которым проводятся измерения, должны быть теми же самыми прямыми, принятыми в алгоритме реконструкции как направления сбора экспериментальных данных.
Имеются также и другие источники возможных ошибок при снятии измерений, однако их рассмотрение выходит за рамки данной книги.
Любое математическое моделирование сложного процесса складывается из двух этапов:
1. моделирование процесса получения проекционных данных,
2. моделирование процесса реконструкции.
Основные проблемы при построении моделей связаны с переходом на дискретную сетку при задании объекта, описании получения проекционных данных и т.д
 |
Рисунок 5.25 - Переход на дискретную сетку задания объекта
Переход от декартовой системы координат на дискретной сетке, в которой задана функция ![]() (томографический фантом) к полярной системе координат, в которой задано уравнение зондирующих лучей осуществляется преобразованием Радона от фантома для различного числа ракурсов. При этом надо ответить на ряд вопросов:
(томографический фантом) к полярной системе координат, в которой задано уравнение зондирующих лучей осуществляется преобразованием Радона от фантома для различного числа ракурсов. При этом надо ответить на ряд вопросов:
- сколько поставить приемников (оптимальное число ракурсов)?
- с какой точностью необходимо регистрировать данные?
- с каким качеством делать приемники?
- какой алгоритм реконструкции использовать при заданном количестве ракурсов, приемников регистрации и заданном уровне шумов регистрации?
После реконструкции необходимо сравнить реконструированное изображение с фантомом. Если в реальной томографии качество восстановленного изображения определяется по методу невязки, то при моделировании сравнение можно провести непосредственно.
Реконструкция - это дискретизированное изображение. В случае если это реконструкция, полученная по модельным данным от тест-фантома, то о качестве этой реконструкции судят путем сравнения ее с дискретизированными данными самого фантома. При этом, естественно, кадр изображения и сетка должны иметь одни и те же размеры, как для реконструкции, так и для дискретизации фантома. Этот раздел посвящается обсуждению вопроса о том, как отображают и измеряют различие между реконструкцией и фантомом.
Визуальная оценка является, конечно, наиболее прямым методом. Для этого отображают реконструкционное изображение и изображение фантома и смотрят, все ли интересующие нас характеристики фантома воспроизведены на реконструкции и нет ли ложных деталей, возникших в процессе реконструкции. Недостаток подобной качественной оценки в ее субъективности, так как специалисты довольно часто расходятся во мнении о том, какое из двух изображений точнее воспроизводит третье.
Более точный метод оценки изображений состоит в следующем. Выбираем столбец элизов, проходящий через наиболее существенные детали в оригинале. Например, в цифровом фантоме головы (рисунок 5.26) 63-й столбец из 115 столбцов проходит через желудочки, обе опухоли и гематому. На рисунке 5.26 этот столбец изображен черной вертикальной линией. Один из методов оценки качества реконструкции заключается в сравнении 115 значений плотности в элизах этого столбца в оригинале и реконструкции. Такое сравнение сделано для всех реконструкций фантома головы, приведенных в данной книге.
Лучше всего иметь один параметр, который является мерой близости реконструкции и оригинала. Здесь следует предупредить читателя, что не только один параметр, но даже и набор из нескольких параметров не могут описать всех характеристик отличия двух изображений. Последовательность приближения реконструкций к оригиналу, выбранная на основе измерения только одного параметра, может оказаться ложной.
63-й столбец из 115 столбцов изображен черной вертикальной линией
Рисунок 5.26- Фантом головы
В данной книге приведены три меры различия между изображениями. Чтобы определить эти меры, обозначим через tu,v и ru,v плотности v-гo элиза в u-й строке матрицы тест-фантома и реконструкции соответственно, ![]() —среднее значение плотности в дискретизации тест-фантома. Мы предполагаем, что обе эти матрицы изображения имеют размер l х l, причем [l /2] равно наибольшему целому числу, но не более l/2. Меры различий, определяемые выражениями (5.29) — (5.33), часто используют в литературе по томографии:
—среднее значение плотности в дискретизации тест-фантома. Мы предполагаем, что обе эти матрицы изображения имеют размер l х l, причем [l /2] равно наибольшему целому числу, но не более l/2. Меры различий, определяемые выражениями (5.29) — (5.33), часто используют в литературе по томографии:
 (5.29)
(5.29)
![]() (5.30)
(5.30)
![]() (5.31)
(5.31)
где
![]() (5.32)
(5.32)
![]() (5.33)
(5.33)
Приведенные выше три меры различия выражают разные аспекты качества изображения. Первая из них, d-мера, является нормированной среднеквадратичной мерой различия. Большое различие значений в небольшой области ведет к высокому значению d. Отметим, что d=1 тогда, когда реконструкции представляют собой правильное воспроизведение изображения с равномерно распределенной средней плотностью. Вторая мера, r-мера, является нормированной абсолютной средней мерой различия. В противоположность d-мере r-мера фиксирует наличие большого числа малых ошибок, нежели малого числа больших ошибок. Отметим, что r = 1 тогда, когда реконструкции имеют плотность, равную нулю по всем элизам. Третья мера, е-мера, соответствует различию в наихудшем случае. Ее значение равно наибольшей разнице в плотности между [l/2] х [ l/2]-матрицами тест-фантома и реконструкции. При вычислении е-меры мы используем более грубую дискретизацию, чем та, которая была использована для реконструкции, так как размер наименьших деталей в рассматриваемом фантоме равен нескольким элизам, и на практике мы обычно пользуемся усредненными значениями плотности в этих элизах для оценивания относительного линейного ослабления ткани или опухоли, которые нас интересуют. е-Мера обеспечивает нас гарантированной надежностью такой оценки. Все три меры будут приведены для всех реконструкций в данной книге.
Реальной мерой достоверной процедуры реконструкции являются ее характеристики, полученные в практике медицинской диагностики. К сожалению, эту меру трудно определить количественно, и поэтому в качестве одного из подходов используют рабочие характеристики приемника, о которых в данной книге ничего не говорится.
На рисунке 5.27- представлена модуляционная передаточная функция.
 |
1 – СТ7800(IIп)
2 – СТ8800(IIIп)
3 – ЕМИ(IIIп)
Рисунок 5.27 - МПИ - Модуляционная передаточная функция
Погрешности вызваны :
- Объектом исследования (его движение, взаимодействие, изменение плотности)
- Механическими узлами сканирования
- Рентгеновским излучателем (размер рентгеновской трубки, однородность пучка излучения)
![]() - однородность пучка изменения
- однородность пучка изменения
- Коллиматором
- Детектором
- Алгоритмы, их реконструкции
- Методы предварительной обработки информации
МПФ определяется экспериментально на фантомах.
Реконструкция томографии представляет собой дискретное изображение. При исследовании томографов проводят сравнение реконструированной томограммы с математическим фантомом.
Сравнение бывает визуальным:

Вводят следующие характеристики:
1)  - нормированная среднеквадратическая мера различия
- нормированная среднеквадратическая мера различия
Фактически, d говорит об артефактах, т.е. есть зоны, где d велико.
2) 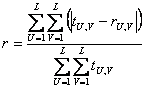 - нормированная абсолютная мера различия
- нормированная абсолютная мера различия
Фиксирует наличие большого числа малых ошибок.
3) ![]()

e – мера, которая соответствует различию в наихудшем случае.
На рисунке 5.28 показано какое влияние на погрешность оказывает движение пациента.
Метод борьбы – круговое сканирование объекта, т.е. увеличение угла обзора. Хаунcфилд ввел число для оценки качества томограмм.
 |
а – линейное движение
б – движение перестатики
в – легочное движение
г – сердечно-сосудистое движение
Рисунок 5.28
|
|