Обработка результатов имитационного эксперимента

Современные системы имитационного моделирования предоставляют возможность выполнять автоматически стандартную обработку результатов моделирования:

• определение характеристик случайных параметров, главным образом, их матожиданий и дисперсий;
• фиксация минимальных и максимальных значений исследуемых величин;
• частотное распределение результатов измерений (построение гистограмм);
• расчет коэффициентов использования объектов модели и др.

Часто инженеру приходится выполнять более сложную обработку:

• определение функциональных или статистических зависимостей между исследуемыми величинами;
• выявление существенных или несущественных факторов, участвующих в эксперименте;
• сравнение случайных параметров процесса с целью определения значимости расхождения или совпадения их характеристик и др.

В наиболее развитых системах моделирования предусмотрены средства, обеспечивающие выполнение этих обработок. Но в любом случае инженер должен понимать сущность обработки, уметь правильно готовить исходные данные, грамотно интерпретировать результаты обработки. При наличии альтернатив обоснованно выбирать метод обработки и, при необходимости, разрабатывать соответствующие процедуры.

Характеристики случайных величин и процессов

По этим данным нужно дать всестороннее описание величины a.

Определить случайную величину - это значит определить ее характеристики. В общем случае:

где - оценка характеристики случайной величины. Под характеристикой понимают следующее.

Во-первых, это характеристика величины:

• матожидание (среднее арифметическое);
• медиана (срединное значение);
• мода (наиболее вероятное значение);
• среднее геометрическое и др.

В рамках задач, характерных для нашей профессии, наиболее актуальным является матожидание. Как известно, матожидание определяет центр рассеивания случайной величины, наиболее полно отмечающее ее положение на числовой оси. Будем обозначать матожидание случайной величины так: .

Во-вторых, это характеристики рассеивания:

• дисперсия (матожидание квадрата отклонения случайной величины a );
• среднее квадратическое отклонение (квадратный корень из дисперсии); иногда целесообразно пользоваться этой характеристикой, так как она имеет размерность самой случайной величины;
• размах ( ).

В-третьих, это характеристика связи между случайными величинами (корреляция); степень связи определяется величиной коэффициента корреляции . В случайном процессе связь между значениями случайной функции в моменты времени , определяет коэффициент автокорреляции

В-четвертых, это характеристика закона распределения вероятностей случайной величины в виде плотности или функции распределения: или .

5.2. Требования к оценкам характеристик

Ограниченное число реализаций модели не позволяет точно определить значения этих характеристик, а только приближенно,

то есть так называемые оценки характеристик \Theta . Степень приближения оценок зависит от методов их вычислений (формул). Поскольку , где - случайные значения искомого параметра, то величина - случайная со своими значениями матожидания, дисперсии и т. п.

Как правило, математическая статистика может предложить разные формулы для вычисления оценки одной и той же характеристики. Следовательно, оценки могут быть более или менее точными или даже вовсе непригодными при имитационном моделировании.

Чтобы оценка наилучшим образом представляла искомую характеристику, нужно, чтобы она обладала следующими свойствами:

• несмещенностью;
• состоятельностью;
• эффективностью.

Несмещенность. Это свойство означает, что оценка не содержит систематической ошибки. Т. е., математическое ожидание оценки совпадает с действительным значением характеристики :

Состоятельность. Это свойство означает, что оценка приближается сколь угодно близко к истинному значению характеристики по мере увеличения объема выборки, т. е. увеличения числа реализаций модели. Формально это свойство записывают так:

при и любом .

Именно это свойство являлось определяющим при нахождении количественной связи между точностью, достоверностью оценок и числом реализаций модели.

Эффективность. Это свойство означает, что из всех несмещенных и состоятельных оценок следует предпочесть ту, у которой разброс значений меньше. Иначе: эффективной оценкой характеристики случайной величины называют ту, которая имеет наименьшую дисперсию:

- число возможных оценок.

В исследовании свойств оценок большая заслуга принадлежит англичанину Рональду А. Фишеру. Основные результаты он получил в 1912 г., когда ему было 22 года.

5.3. Оценка характеристик случайных величин и процессов

Наиболее используемые оценки характеристик приведены в табл. 5.1.

Таблица 5.1. Характеристики случайных величин и их оценки

Характеристика	Оценка	Среднее квадратическое отклонение оценки
Матожидание
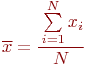Дисперсия
Среднее квадратическое отклонение
Вероятность события
Коэффициент корреляции

Все оценки несмещенные, состоятельные, эффективные.

Проблемами оценок занимался и Абрагам Вайльд, американский математик австрийского происхождения.

Приведем для иллюстрации два примера.

Пример 5.1. Оценка матожидания случайной величины - среднее арифметическое

является несмещенной, состоятельной и эффективной.

Оценка в виде медианы не является эффективной, так как дисперсия в этом случае

в раз больше дисперсии , равной, как известно,

Пример 5.2. Выборочная дисперсия случайной величины

состоятельна, эффективна, но смещена. Смещение образовалось из-за того, что вместо неизвестного в формуле стоит оценка

Несмещенная оценка имеет вид:

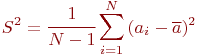
Иногда формулы для вычисления оценок матожидания и дисперсии используют в рекуррентной форме:

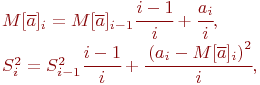
где - оценки матожидания и дисперсии, вычисленные по данным и ( ) реализаций имитационной модели.

Приведенные в табл. 5.1, формулы соответствуют нормальному закону распределения вероятностей исследуемой величины.

При исследовании случайного процесса весь временной интервал представляется последовательностью из временных точек , , в каждой из которых измеряется значение сечения . Индекс - номер реализации случайного процесса, .

Полученные данные образуют матрицу сечений размером , что и является моделью исследуемого процесса (табл. 5.2).

Таблица 5.2. Результаты исследования случайного процесса

Реализации	Временные точки

Совокупность сечений в каждой временной точке (столбец матрицы), представляет собой случайные числа некоторой случайной величины в общем случае со своими законами распределения, матожиданиями, дисперсиями:

При решении практических задач последовательности этих оценок матожиданий и дисперсий, определенных в точках , достаточно полно представляют моделируемый случайный процесс. Оценки матожиданий и дисперсий можно аппроксимировать подходящими кривыми в предположении непрерывности процесса.

Иногда исследователя интересует связь сечений случайного процесса между собой. Степень зависимости между сечениями определяет автокорреляционная функция. Оценка ее имеет вид:

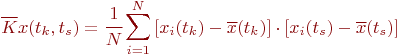(t_s)])

где и - значения сечений в точках и соответственно -й реализации;

и - оценки матожиданий совокупности сечений в точках и соответственно.

Данные расчета значений автокорреляционной функции , , помещают в таблицу, которая и является табличным определением ее. В случае необходимости данные таблицы могут быть представлены подходящей аппроксимирующей кривой.

Пример таблицы значений для случайного процесса,

определенного пятью сечениями , показан в табл. 5.3.

Таблица 5.3. Значения автокорреляционной функции

	Временные точки

Очевидно, что рассчитывать все значения для заполнения таблицы (в данном примере их 25) не надо, так как значения при ("северо-западная диагональ") представляют собой значения соответствующих дисперсий. И , что исключает необходимость расчета половины оставшихся значений коэффициентов автокорреляционной функции, расположенных выше или ниже упомянутой диагонали.

Гистограмма

Одной из задач моделирования может быть определение закона распределения вероятностей исследуемой случайной величины и количественных значений его характеристик.

Аналогом, моделью плотности распределения вероятности случайной величины является гистограмма, которую можно построить (аналитически или графически) по данным имитационного моделирования.

Гистограмма (рис. 5.1) строится так.

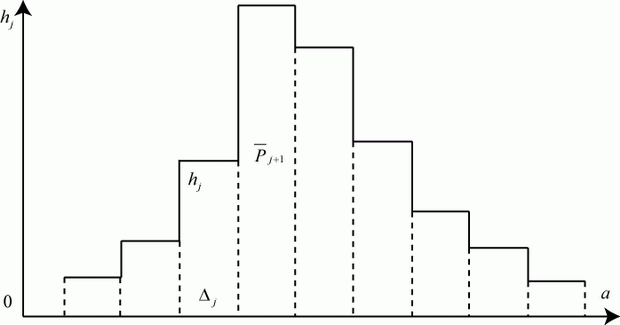
В результате реализаций модели получен ряд случайных значений исследуемого параметра : . Весь диапазон значений разбивается на интервалов (разрядов). Числовой диапазон каждого интервала обозначим , . Обычно все числовые диапазоны одинаковые: .

Для каждого интервала подсчитываем число значений , попавших в него - .

На каждом интервале строят прямоугольник с высотой :

Площадь каждого прямоугольника гистограммы равна относительной частоте :

По выбору числа интервалов существуют разные эмпирические рекомендации, например:

Чем больше и , а меньше , тем ближе гистограмма совпадает с некоторым теоретическим распределением. Доказал это Валерий Иванович Гливенко - известный отечественный математик.

На основе очертания гистограммы делается предположение (выдвигается гипотеза) о совпадении полученного эмпирического распределения вероятностей с тем или иным теоретическим - нормальным, экспоненциальным, Вейбулла и т. д. Затем выполняется проверка этой гипотезы с помощью критериев согласия.В курсе высшей математики рассматриваются некоторые (критерий Колмогорова, критерий Смирнова и др.), наиболее популярными считают критерий хи-квадрат - критерий Пирсона, предложенный в 1903 г.

Оценки матожидания и дисперсии можно получить по данным гистограммы:

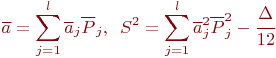
где - среднее значение каждого интервала;

- оценка по каждому интервалу;

- поправка Шеппарда.

5.4. Элементы дисперсионного анализа. Критерий Фишера

Приведем понятия, которые используем в дальнейшем. В математической статистике (а это основной математический аппарат обработки результатов моделирования) широко используется понятие гипотезы.

Гипотезой называется предположение о:

• законах распределения вероятностей случайных величин;
• значениях характеристик случайных величин;
• совпадении законов распределения двух и более случайных величин и др.

Обычно исходную гипотезу называют нулевой и обозначают Противоположное утверждение называют конкурирующей гипотезой и обозначают

Гипотеза подвергается проверке. Смысл этой проверки в том, чтобы принять или отклонить ее с допустимым минимальным риском. При этом возможны ошибки:

• забраковать проверяемую гипотезу, если она верна, что соответствует так называемой ошибке первого рода ;
• принять проверяемую гипотезу, когда она не верна,значит совершить ошибку второго рода.

Правило, которому принимается суждение об истинности или ложности основной гипотезы называют критерием проверки или критерием согласия.

В практике моделирования и обработки экспериментальных данных очень часто необходимо решать проблему подтверждения или опровержения гипотезы о принадлежности двух или более выборок одной генеральной совокупности.

К такой проблеме приводят такие задачи:

• сравнительная оценка различных технологических процессов по их производительности, точности, экономичности;
• сравнение конструктивных особенностей приборов, машин, средств вооружения и др.

Признаки, по которым проводится сравнительная оценка, часто не являются детерминированными, обладают рассеиванием. Например, точность никогда не может быть абсолютной, так как измерительные приборы всегда несут в себе ошибку.

Наиболее общим и часто применяемым на практике методом сравнения качеств объектов является дисперсионный анализ.

Сущность дисперсионного анализа состоит в проверке гипотезы о тождественности выборочных дисперсий одной и той же генеральной дисперсии.

Почему исследователей интересует сравнение именно дисперсий, а не каких-либо других характеристик? Заметим, что есть методики сравнения, например, матожиданий и др., но они не обладают такой общностью, как дисперсионный анализ.

А дело в том, что дисперсия характеризует важные конструкторские и технологические показатели как:

• точность приборов;
• рассеивание точек попадания при стрельбе и др.

И еще дисперсионный анализ одновременно решает проблему проверки гипотезы о равенстве средних значений выборок.

Задача сравнения дисперсий сводится к проверке исходной гипотезы (нулевой гипотезы ) о принадлежности двух выборок

одной и той же генеральной совокупности.

Для проверки гипотезы о равенстве дисперсий нужно иметь независимую функцию, вычислимую по данным эксперимента.

Такой функцией является функция Фишера (распределение Фишера, F -распределение), определяемая так:

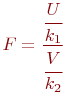
где и случайные величины, имеющие распределение ;

и соответствующие степени свободы случайных величин и соответственно, , ;

и - количество испытаний (объемы выборок).

Почему является мерой сравнения дисперсий? А потому, что дисперсии, являясь суммой квадратов ошибок, имеют распределение .

Распределение хи-квадрат определяется следующим образом:

где - число степеней свободы, - число Эйлера (2,71:), - гамма-функция.

График плотности F -распределения показан на рис. 5.2.

Итак, случайная величина

где и - несмещенные оценки дисперсий, полученных из независимых выборок, взятых из нормальных совокупностей, имеет распределение Фишера ( F -распределение).

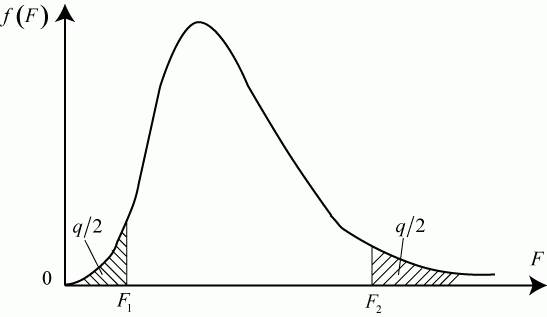
Величина F - случайна, поэтому судить однозначно по ее величине о подтверждении или опровержении гипотезы об однородности исследуемых выборок нельзя.

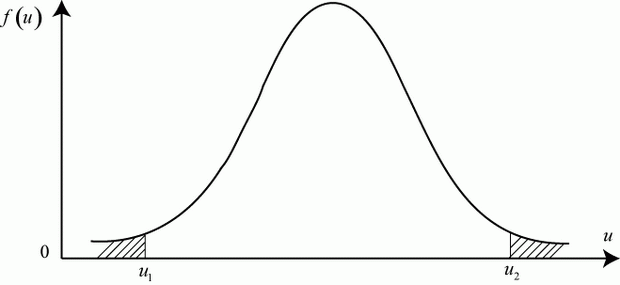
Поэтому вводится уровень значимости, численно равный вероятности неприемлемых отклонений от принятой гипотезы. Области неприемлемых значений показаны на рис. 5.2 штриховкой. Граничные точки допустимых значений определяются точками и , соответствующих вероятностям .

Если вычисленное по данным эксперимента значение попадает в область между точками и :

то принятая гипотеза не опровергается.

Заметим, что случайная величина

также имеет F -распределение со степенями свободы и соответственно. Следовательно, вероятность попадания числа в левую критическую область равна:

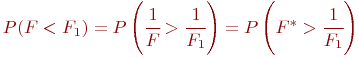
Отсюда следует, что левая критическая точка F -распределения соответствует правой критической точке -распределения. Т. е. правые точки распределений и определяют левую и правую точки и . Поэтому в таблицах представлены только правые критические точки F -распределения.

В таблицах значения приведены в зависимости от , числа степеней свободы и .

Обычно при вычислении в числитель отношения ставят значение большей дисперсии.

Итак, при принятая гипотеза не опровергается, при - не подтверждается.

Пример 5.3. В часть поступили две буссоли. Первая из них при измерении пять раз одного и того же угла показала дисперсию . По результатам семи измерений второй буссолью того же угла получена дисперсия .

Однотипны ли буссоли? Одинаковы ли они по точности измерения углов? Выдвинем и проверим гипотезу об их однотипности для уровня значимости

Решение

По таблицу F -распределения для степеней свобод , соответствующей большей дисперсии, и , соответствующей меньшей дисперсии, и уровню значимости , находим .

Так как , то для уровня значимости гипотеза об одинаковости буссолей не опровергается.

Итак: чем меньше уровень значимости , тем меньше вероятность забраковать проверяемую гипотезу, когда она верна, т. е. совершить ошибку первого рода.

Но с уменьшением уровня значимости (увеличения ) расширяется область допустимых ошибок, что приводит к увеличению вероятности принятия неверного решения,т. е. совершения ошибки второго рода.

В заключение изложенного отметим, что как бы ни был велик объем статистического материала и критерий Фишера (впрочем, как и любой другой) не может дать абсолютно достоверный ответ о справедливости или несправедливости проверяемой гипотезы, так как мы оперируем случайными числами.

То есть, опровержение гипотезы ни в коем случае не означает категорического, логического опровержения гипотезы при , равно как и подтверждение гипотезы при не означает категорического доказательства ее справедливости. Не исключено, что в том и в другом случае решение может оказаться ошибочным.

Суждение о подтверждении или отклонении выдвинутой гипотезы высказывается с определенной степенью достоверности.

Среди инженеров бытует шутливое изречение: статистика, как фонарный столб на улице: света дает мало, но при случае на него можно опереться.

Но свет-то дает! И другой альтернативы нет.

Критерий Вилькоксона

Как и в предыдущем случае решается следующая задача. Имеются две серии независимых наблюдений однородных случайных величин и , причем значения и дают различные значения средних или (и) различные рассеивания. Возникает вопрос: можно ли считать эти расхождения существенными или расхождения зависят от случайных выборок?

Простой в употреблении и вполне приемлемый по точности критерий для проверки гипотезы о тождественности функций распределения и предложил в середине прошлого века Вилькоксон. Критерий назван его именем.

Рассматривается нулевая гипотеза: . Конкурирующая гипотеза: .

Критерий основан на подсчете числа инверсий. Инверсии определяются так.

Измеренные значения и , располагаются в общую последовательность в порядке возрастания их значений. Пусть это будет, например, так:

где - члены, принадлежащие первой выборке;

- члены второй выборки. Эта последовательность - не убывающая, содержащая чисел, - количество чисел последовательности , - последовательности .

Если гипотеза верна, то достаточно очевидно, что числа из обеих последовательностей хорошо перемешиваются. Степень перемешивания определяется числом инверсий членов первой последовательности относительно второй. Если в упорядоченной общей последовательности некоторому предшествует одно значение , это означает, что имеет место одна инверсия.

Если некоторому предшествуют значений , то это значение имеет инверсий.

Для нашего примера член имеет одну инверсию с ; член - тоже одну с ; член имеет четыре инверсии (с ); член имеет шесть инверсий (с ).

Таким образом, общее число инверсий:

Показано, что случайная величина уже при и дает хорошее приближение к нормальному распределению с матожиданием и дисперсией:

При уровне значимости и нормальности распределения вероятность попадания значения в критическую область (что означает не подтверждение нулевой гипотезы) равна:

Отсюда следует, что левая критическая граница и правая критическая граница (рис. 5.3) равны соответственно:

- функция Лапласа, с которой мы встречались ранее, она табулирована. Наиболее актуальные соответствия уровней значимости и аргументов функции Лапласа указаны в табл. 5.4

Таблица 5.4. Уровни значимости и аргументы функции Лапласа

	2	5	10
	2,33	1,96	1,65

Пример 5.4. С целью проверки адекватности модели центра коммутации сообщений измерено время задержки передачи сообщений на модели центра и непосредственно на самом центре. Результаты измерений сведены в табл. 5.5.

Таблица 5.5. Результаты измерений задержки сообщений

, сек	0,8	1,9	3,0	3,5	3,8	2,5	1,7	0,9	1,0	2,3
, сек	1,4	2,1	3,1	3,6	2,7	1,8	1,1	0,2	1,6	2,8

Последовательность - отклики модели, - данные, измеренные на центре. Проверка адекватности модели состоит в проверке нулевой гипотезы, то есть в том, что данные измерений идентичны в статистическом смысле. Решение

Составим в порядке возрастания общую последовательность времен задержек и (табл. 5.6).

Таблица 5.6. Общая последовательность времен задержек сообщений

0,2	0,8	0,9	1,0	1,1	1,4	1,6	1,7	1,8	1,9
2,1	2,3	2,5	2,7	2,8	3,0	3,1	3,5	3,6	3,8

Расчет числа инверсий для :

Расчет характеристик:

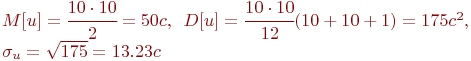
Примем уровень значимости . Тогда

Правая критическая точка:

Левая критическая точка:

Проверка гипотезы :

Гипотеза об идентичности распределений времен ожиданий в модели и в объекте не опровергается.

В заключение отметим, что при малых и ( ) для критерия Вилькоксона составлены таблицы критических точек и для различных уровней значимости . Эти таблицы приводятся в широко известных изданиях, например, Б. Л. ван дер Варден "Математическая статистика", Б. В. Гнеденко и др. "Математические методы в теории надежности".

Однофакторный дисперсионный анализ

В современной жизни - военной и гражданской часто возникают проблемы, решение которых требует научного обоснования.

Однотипны ли патроны для конкретного образца стрелкового вооружения, выпускаемые на разных заводах?

Однородны ли, например, автоматы, выпускаемые на разных заводах?

Здесь в качестве исследуемого фактора выступают заводы. Разные, но однотипные по назначению - варианты фактора, которые можно трактовать как уровни факторов.

Аналогичная задача возникает при сравнении однотипных изделий, вырабатываемых с применением различных технологий. Здесь подлежит анализу фактор - технология производства.

Эти и подобные задачи являются задачами однофакторного дисперсионного анализа (ОДА).

Иногда возможны задачи одновременного исследования влияния двух и более факторов. Например, чем объяснить рассеивание попаданий в цель: конструкторскими особенностями стрелкового вооружения, выпущенного на разных заводах, или различиями в подготовке стрелков?

Исследованием влияния факторов и занимается факторный дисперсионный анализ.

Мы рассмотрим ОДА, наиболее актуальный анализ на практике. Теория рассматривает и многофакторный дисперсионный анализ. В нем процедуры подобны тем, которые мы рассмотрим в ОДА. Усложняются только расчеты и при необходимости, зная ОДА, овладеть методикой многофакторного дисперсионного анализа, не составит труда.

Эксперимент для выполнения ОДА состоит в накоплении результатов измерений контролируемого параметра (угла, расстояния, наработки на отказ некоторого изделия и т. д.) при каждом варианте исследуемого фактора.

Введем обозначения:

- число вариантов фактора;

- число измерений при каждом варианте;

- результат каждого измерения;

- номер варианта фактора;

- номер измерения.

Схема эксперимента заключается в следующем.

Производится измерений контролируемого параметра при вариантах фактора.

В принципе, число измерений может быть разным для каждого варианта фактора. Ход дальнейших рассуждений от этого не меняется.

Результаты эксперимента сводятся в таблицу (табл. 5.7).

Вопрос: влияют ли варианты фактора на точность измерений? Или, говоря языком математической статистики, являются результаты измерений выборкой одной генеральной совокупности, или нет? Если да, то варианты фактора несущественны, если нет, то существенны.

Будем исходить из следующей нулевой гипотезы:

• наблюдения каждого варианта независимы;
• наблюдения каждого варианта имеют нормальное распределение;
• имеют одинаковую дисперсию ;
• имеют одинаковые центры рассеивания.

Таблица 5.7. Результаты эксперимента

№ варианта	Номер измерения						Средние значения

Очевидно, если систематические ошибки вариантов не одинаковы, следует ожидать повышенного рассеивания выборочных средних .

Для подтверждения или отрицания выдвинутой нулевой гипотезы об идентичности вариантов фактора проведем дисперсионный анализ.

Общее среднее арифметическое по всем измерениям:

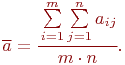
Сумма квадратов отклонений по всем измерений, то есть по данным всего эксперимента:

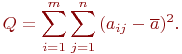
Эту сумму квадратов отклонений можно разложить на два независимых слагаемых:

Обозначим:

Что такое и

- сумма квадратов отклонений между вариантами фактора, так как - среднее значение измеренного параметра -го варианта фактора;

- характеризует отклонения внутри каждого варианта.

Если принятая гипотеза о равенстве центров рассеивания и дисперсий верна, тогда все наблюдений значений можно рассматривать как выборку из одной и той же нормальной совокупности с очевидной несмещенной оценкой дисперсии:

Можно показать, что величина

имеющая распределение со степенями свободы , является оценкой дисперсии

И величина

имеющая распределение со степенями свободы , также является оценкой дисперсии .

Из сказанного следует, что критерий

при нашей гипотезе и независимости и (это можно доказать) имеет F -распределение с и степенями свободы.

А дальше мы уже знаем, как поступить:

• выбираем уровень значимости ;
• вычисляем число ;
• из таблицы по величине находим .

Если окажется

то есть мы попали в область маловероятных значений , то выдвинутая гипотеза не подтверждается.А это значит, что варианты фактора не однотипны. Но если

то гипотеза об однородности вариантов фактора подтверждается, конечно, в рамках допустимого риска.

Пример 5.5. Необходимо проверить однотипность патронов к автомату Калашникова, изготовленных на трех заводах.

Для получения необходимых для дисперсионного анализа данных автомат закрепили в специальном станке и сделали из него по 50 выстрелов патронами каждого завода. По результатам стрельбы измерялись радиальные отклонения пробоин от точки прицеливания.

Результаты измерений приведены в табл. 5.8.

Решение

Проверяем исходную гипотезу: патроны, выпускаемые на трех разных заводах, баллистически однотипны.

При выборе уровня значимости исходим из того, что более опасна ошибка второго рода - подтвердить ошибочный выбор. Примем .

Число вариантов фактора:

Число измерений: .

При вычислениях опустим очевидные элементарные арифметические детали.

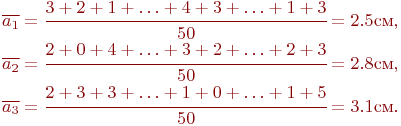
Средние отклонения пробоин при стрельбе патронами заводов № 1, № 2, № 3 равны соответственно:

Среднее отклонение по 150 выстрелам:

Средний квадрат расхождений между вариантами факторов:

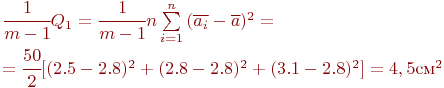
Число степеней свободы: .

Средний квадрат расхождений внутри вариантов:

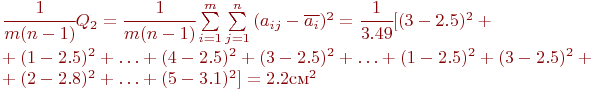
Число степеней свободы:

Расчет F -критерия:

По табл. П.2 при верхних пределов уклонения величины и имеющихся степенях свободы 2 и 147 находим . Величина определена при , так как табличные значения при не определены. Нетрудно убедиться, что такое приближение вполне допустимо.

Поскольку , делаем вывод о том, что выдвинутая гипотеза об однотипности партий патронов, выпускаемых тремя разными заводами, не опровергается (в пределах принятого уровня значимости).

Выявление несущественных факторов

Большое количество факторов усложняет и снижает эффективность эксперимента. Среди этого множества могут быть и несущественные факторы. Исключение их упростило бы эксперимент, не снижая его информативности.

Несущественный фактор выявляется так.

Выполняются первый эксперимент из наблюдений с учетом проверяемого фактора и второй эксперимент также из наблюдений - без него. В обоих случаях фиксируются отклики . Делается предположение, что обе выборки принадлежат одной генеральной совокупности, то есть, что проверяемый фактор - несущественный (это нулевая гипотеза). Дальнейшие рассуждения должны либо не опровергнуть эту гипотезу, либо посчитать ее недостаточно обоснованной.

Итак, получены две последовательности откликов, в которой и - значения откликов в -м наблюдении при наличии и отсутствии проверяемого фактора соответственно:

Согласно принятой гипотезе эти последовательности имеют одинаковые матожидания и дисперсии .

Рассмотрим случайную величину , реализациями которой является последовательность случайных чисел

При независимости и достаточно большом числе наблюдений согласно центральной предельной теореме:

Очевидно:

Как отделить случайные отклонения от нуля от тех, которые мы будем считать не подтверждающими принятую гипотезу?

Такое разделение осуществляется по следующему правилу: если вычисленная величина окажется маловероятной, в рамках нормального распределения и данном среднеквадратическом отклонении , то такое отклонение от нуля считается не соответствующим принятой гипотезе.

Эту малую вероятность называют уровнем значимости и обозначают . Обычно - в зависимости от степени опасности совершения ошибки первого или второго рода.

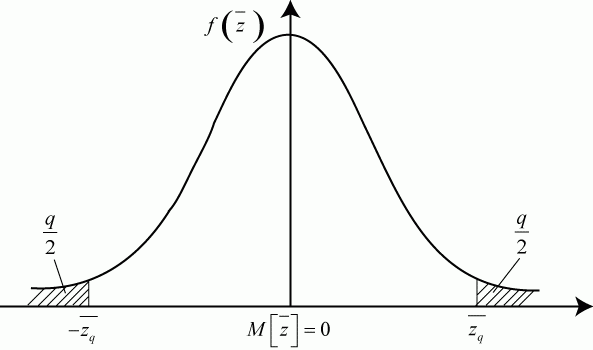
На графике плотности распределения уровень значимости показан заштрихованным участком (рис. 5.4).

Для нормального закона распределения случайной величины вероятность превышения некоторого значения определяется известным выражением:

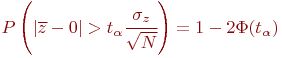
где - функция Лапласа.

• граничное значение
• 

Аргумент функции Лапласа находим из соответствующего справочника согласно 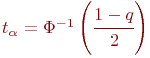и, как было указано ранее,

Из изложенного следует:

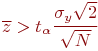• если , принятая гипотеза о несущественности проверяемого фактора не подтверждается;
• если , принятая гипотеза не опровергается (в рамках принятого уровня значимости ).

Обычно величина неизвестна, поэтому следует использовать ее оценку :

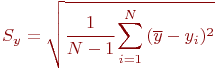
Оценку и ряд значений можно получить из данных первого эксперимента ( ) или второго ( ), так как в силу рассматриваемой гипотезы они идентичны. Однако следует помнить, что если то вместо аргумента функции Лапласа надо брать - аргумент функции Стьюдента.

Пример 5.6. Исследуется зависимость времени пребывания заявки в системе массового обслуживания от дисциплины выборки заявок из очереди: LIFO или FIFO. Проведены два эксперимента. Первый эксперимент из наблюдений с дисциплиной FIFO и второй эксперимент также из наблюдений с дисциплиной LIFO.

Решение

Выдвигается гипотеза о несущественности влияния на время пребывания заявки в системе массового обслуживания изменения дисциплины FIFO на LIFO.

Результаты измерений и вычислений:

• , ;
• для уровня значимости ,

Так как то гипотеза не подтверждается. Для времени пребывания заявки в очереди в системе массового обслуживания не безразлично, какая дисциплина выборки заявок из очереди применена.

В заключение отметим, что рассмотренную проблему можно решать и методом однофакторного анализа. Однако если (при сравнении двух выборок) целесообразно использовать изложенный метод.

Сущность корреляционного анализа

Часто при исследовании объекта или его модели необходимо наблюдать за характеристиками двух и более случайных величин. Например, за двумя откликами одного эксперимента. При этом может возникнуть вопрос: есть ли связь между этими случайными величинами? Существенна или несущественна эта связь, если она есть?

Корреляционный анализ - это совокупность методов обнаружения зависимости (корреляции) между двумя или более случайными признаками или процессами.

Под корреляцией будем понимать статистическую зависимость между двумя случайными величинами, не имеющую, вообще говоря, строго функционального характера.

Заметим, что корреляционный анализ не позволяет определить вид функциональной связи между случайными величинами, а только наличие или отсутствие предполагаемой связи, например, линейной, параболической, экспоненциальной и т. д. В рамках этого учебного пособия мы ограничимся рассмотрением гипотезы о наличии линейной корреляции.

Определение вида функциональной связи между величинами рассматривается в регрессионном анализе, элементы которого и практическое использование будут рассмотрены в следующем п. 5.10.

Название "корреляционный анализ" происходит от латинского слова correlatio - согласование, связь, соотношение, взаимосвязь. Термин впервые введен Гальтоном (Galton) в 1888 г.

Обычно исследуют парную корреляцию, то есть зависимость между двумя случайными величинами (процессами), хотя возможны и более сложные ситуации, когда необходимо обнаружить наличие или отсутствие связей между тремя или более случайными величинами.

Мы ограничимся исследованием парной корреляции.

Как известно, связь между двумя случайными величинами можно описать с помощью двумерной функции распределения. Однако такое описание часто очень сложно, а для практических целей можно удовлетвориться определением зависимостей средних значений.

Итак, целью имитационного эксперимента является определение характеристик двух случайных величин и . Например:

Средний балл успеваемости учебной группы по математике	Средний балл выполнения упражнения по стрельбе
Рассеивание точки падения заряда по дальности	Рассеивание точки падения заряда по боковому отклонению
Вес курсантов (студентов).	Успеваемость по физподготовке.

Необходимо проверить: есть ли связь между величинами и ?

Проверка наличия (или отсутствия) связи - корреляции - между случайными величинами выполняется так.

Проводится два эксперимента, каждый - с соответствующей моделью. В каждом эксперименте - наблюдений (напоминаем, что компьютерный эксперимент состоит из наблюдений, а наблюдение - из реализаций (прогонов) модели, число которых рассчитывается с учетом требуемой точности и достоверности получаемых результатов моделирования). В результате экспериментов получаются два множества значений измеряемых параметров и : и , .

Из этих множеств формируются пары:

Каждая пара интерпретируется как координаты случайной точки в системе координат , .

Первичное исследование можно провести графически. Возможны следующие варианты размещения точек на графиках (рис. 5.5).

Корреляция - важное понятие. Научитесь визуально определять по расположению данных, насколько тесно они коррелированны.

Говорят, что две переменные положительно коррелированны, если при увеличении значений одной переменной увеличиваются значения другой переменной (рис. 5.5б).

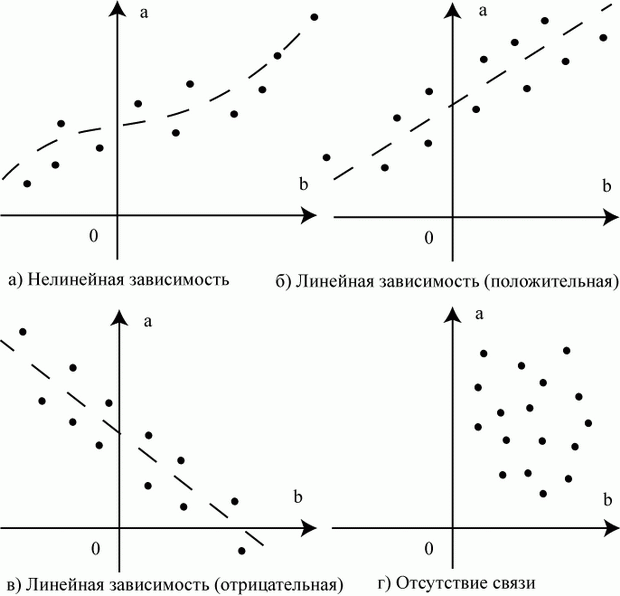
Две переменные отрицательно коррелированны, если при увеличении одной переменной другая переменная уменьшается (рис. 5.5в).

Отсутствие корреляции - совместного поведения переменных - обнаруживается хаотическим нагромождением точек, исключающим проведение какой-либо аппроксимирующей линии (см. рис. 5.5г).

Но такое качественное исследование недостаточно. Необходимо иметь количественную оценку степени корреляции между величинами и .

Если совместное распределение вероятностей случайных величин и нормальное, то количественной характеристикой степени линейной связи между ними является коэффициент корреляции r (введен Пирсоном (Pearson), 1896 г.):

Если , то между и линейная независимость.

Равенство свидетельствует о наличии однозначной функциональной связи между и , то есть .

При между и существует стохастическая связь, причем, чем ближе коэффициент корреляции к единице, тем эта связь сильнее. Стохастическая связь означает, что при изменении имеется лишь тенденция к изменению .

Коэффициент корреляции определяется по данным эксперимента, следовательно, можно определить только его оценку . В качестве оценки принят выборочный коэффициент корреляции:

где оценки математических ожиданий и и ;

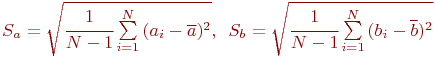- оценки среднеквадратических отклонений и

Выборочный коэффициент корреляции , так же как и теоретический, принимает значения: .

Если , то наблюдается положительная корреляция (см. рис. 5.5б). Если - отрицательная корреляция (см. рис. 5.5в). Если - линейная корреляция отсутствует (но не исключена нелинейная). Если , то между случайными величинами существует жесткая функциональная связь.

Заметим, что рассматриваемый коэффициент корреляции определяет степень линейной связи между случайными величинами и . Эта корреляция наиболее популярна, поэтому часто, когда говорят о корреляции, имеют в виду именно корреляцию Пирсона.

Однако этот линейный коэффициент корреляции не является пригодным для оценки нелинейной связи, если таковая присутствует. При нелинейной зависимости степень связи между случайными величинами устанавливается более сложными характеристиками, например, корреляционным отношением (К. Пирсон).

Числитель выражения (5.1) иногда называют ковариацией - .

Если случайные величины и независимы, они и не коррелированны . Но некоррелированность и не всегда свидетельствует об их независимости. Но если и имеют нормальное распределение, то условие является необходимым и достаточным условием независимости этих величин.

И еще. Наличие корреляции между случайными величинами и не всегда свидетельствует об их взаимосвязи. Дело в том, что при независимости и каждая из них в отдельности зависит от некоторого случайного фактора , но эта зависимость нами не замечена.

Поэтому хорошим тоном после вычисления корреляций является построение диаграмм рассеяния, которые позволяют понять, действительно ли между двумя исследуемыми переменными имеется связь.

Оценка коэффициента корреляции должна быть определена с требуемыми точностью и достоверностью, которые зависят от числа реализаций модели. Найдем эту связь.

В предположении нормальности распределения можно написать:

С выражение (5.2) мы уже знакомы. Здесь:

- точное значение коэффициента корреляции;

- среднеквадратическое отклонение случайной величины ;

- аргумент функции Лапласа

Обычно среднеквадратическое отклонение неизвестно, поэтому нужно брать ее оценку.

При больших выборках оценка среднеквадратического отклонения :

Из (5.2) следует:

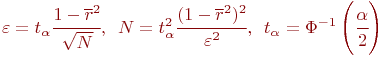
- абсолютная величина ошибки.

Предварительное определение осуществляется по данным пробного эксперимента в количестве реализаций модели.

На основании изложенного и в силу случайного характера исследуемых величин и мы можем утверждать лишь следующее: истинное значение коэффициента корреляции лежит в пределах

с заданной достоверностью .

В заключение отметим, что если совместное распределение случайных величин и не является нормальным, то оценка коэффициента корреляции может выступать в качестве ориентировочной оценки степени тесноты связи и .

Пример 5.7 [2]. Для оценки конструкции нового крупнокалиберного пулемета было произведено 96 выстрелов по щиту, отстоявшему на расстоянии 300 метров.

Результаты отклонений попаданий от точки прицеливания (боковые , по высоте ) объединены в десятисантиметровые диапазоны и сведены в таблицу (табл. 5.9).

Для оценки конструктивных особенностей пулемета необходимо узнать: есть ли какая-то связь между боковыми отклонениями и отклонениями по высоте.

Решение

Ответ на поставленный вопрос может дать коэффициент корреляции. Предварительно заметим, что группировка измерений в десятисантиметровые диапазоны вносит некоторую ошибку в дальнейшие расчеты, однако можно показать, что при данной группировке ошибка несущественна.

В табл. 5.9 указаны не реальные отклонения, а центры диапазонов (-25:-15, -15:-5, -5:5 и т. д.).

Таблица 5.9. Отклонения от точки прицеливания

	Боковые отклонения							Всего
	-20	-10	0	10	20	30	40
-50	0	0	1	0	2	0	0	3
-40	0	1	1	1	2	0	0	5
-30	1	1	3	5	2	1	0	13
-20	1	3	7	3	2	2	0	18
-10	0	2	6	10	3	0	0	21
0	0	1	6	6	6	1	1	21
10	0	0	3	3	3	1	0	10
20	0	1	1	2	1	0	0	5
Всего	2	9	28	30	21	5	1	96

Для определения коэффициента корреляции понадобятся следующие характеристики:

, ковариация .

Все эти характеристики вычисляются по данным измеренных отклонений боковых и по высоте .

Для примера, расчет :

Результаты расчета остальных характеристик:

Теперь оценка коэффициента корреляции:

Среднеквадратическое отклонение этой оценки:

Из-за малого количества выстрелов оценка определена с ошибкой, которая в предположении о нормальном распределении случайной величины и достоверности, например, ( ) равна:

Отсюда следует, что истинное значение коэффициента корреляции лежит в пределах:

Обнаружена небольшая линейная зависимость отклонений боковых и по высоте. Баллистики, отвергая непосредственную корреляцию между отклонениями и , объясняют значение влиянием конструктивных особенностей пулемета. Обнаружена также систематическая ошибка в прицеле: , .

Обработка результатов эксперимента на основе регрессии

Часто целью исследования является определение функциональной связи между факторами и откликом (реакцией модели) по данным, полученным при экспериментах с моделью объекта или непосредственно с объектом. Такая цель достигается регрессионным анализом значений факторов и отклика .

Под регрессией в теории вероятностей и математической статистике понимают зависимость среднего значения какой-либо величины от некоторой другой (других) величины. Регрессионный анализ - это совокупность методов построения и исследования регрессионной зависимости между величинами (в нашем случае между факторами и откликом) по статистическим данным. Статистические данные накапливаются при проведении эксперимента.

Формальная схема эксперимента выглядит так (рис. 5.6).

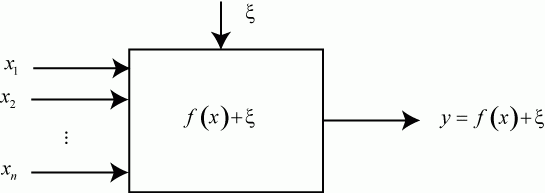
Прямоугольник представляет исследуемый объект или его математическую модель. Обозначения на рис. 5.6:

- значения факторов, ;

- случайный фактор, помеха. Будем считать, что эта случайная величина имеет нормальное распределение с матожиданием . Влияние помехи на отклик аддитивное, то есть ее случайные значения прибавляются к значениям отклика;

- искомая функциональная зависимость между факторами и откликом.

Отклик - величина случайная. представляет собой среднее значение отклика (так как ): .

Исследуемый объект представляется как "черный ящик", никаких предположений о виде функции нет. Поэтому представим ее в виде аппроксимирующего полинома:

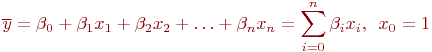
Этот полином получил название уравнения регрессии, а коэффициенты - коэффициенты регрессии. От точности подбора коэффициентов регрессии зависит точность представления .

Коэффициенты определяются путем обработки полученных в ходе эксперимента варьируемых значений факторов и откликов.

Однако из-за ограниченного числа наблюдений точные значения получить нельзя, будут найдены их оценки :

Поэтому уравнение регрессии принимает вид:

Вообще-то метку над теперь надо бы изменить, так как вместо в уравнении теперь стоят , но мы этого делать не будем, чтобы не загромождать изложение новыми значками.

В уравнении регрессии могут участвовать и так называемые "совместные эффекты" ( и т. п.) или степени значений факторов ( и т. п.). Совместные эффекты и степени факторов можно обозначать обобщенным фактором. Например, уравнение регрессии

можно представить так:

Итак, для определения выражения надо:

• выбрать степень аппроксимирующего полинома - уравнения регрессии;
• определить коэффициенты регрессии.

Выбор уравнения регрессии обычно начинают с линейной модели. Например, для двухфакторного эксперимента ее вид:

Если окажется, что такая аппроксимация дает неприемлемые отклонения при сравнении с экспериментальными точками отклика y , то модель усложняется, например, так:

или

и т.д.

Коэффициенты регрессии для выбранного уравнения определяются из условия минимума суммы квадратов ошибок, вычисленных по все экспериментальным точкам. Это делается так. Введем обозначения:

- значение -го фактора в наблюдении номер ;

- значение отклика в -м наблюдении;

- значение отклика, вычисленное по принятому уравнению регрессии и данным .

Очевидно, сумма квадратов ошибок между экспериментальными значениями и вычисленными по уравнению регрессии для всех наблюдений равна:

Для определения минимума ошибки ?возьмем частные производные от по всем неизвестным коэффициентам регрессии , и приравняем их нулю:

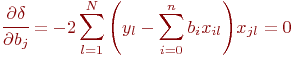
Нетрудно убедиться, что это условие минимума, а не максимума. Очевидно:

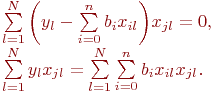
Для лучшей наглядности выделим неизвестные коэффициенты регрессии и получим:

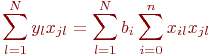
Выражение (5.3) представляет собой систему из уравнений для нахождения неизвестных коэффициентов регрессии , которые окончательно определят выбранное уравнение регрессии.

Нахождение коэффициентов регрессии справедливо при следующих допущениях:

1. Случайный фактор имеет нормальное распределение с матожиданием .
2. Результаты наблюдений - независимые нормально распределенные случайные величины. Если это не соблюдается, то следует измерять другой отклик, удовлетворяющий этому условию, но функционально связанный с исследуемым откликом
3. Точность наблюдений (количество реализаций модели) не меняется от наблюдения к наблюдению.
4. Точность наблюдения должна быть выше точности .

Пример 5.8. На модели объекта проведен однофакторный эксперимент из пяти наблюдений, результаты которого сведены в таблицу (табл. 5.10).

Найти функциональную связь фактора с откликом

Таблица 5.10. Результаты эксперимента

Фактор и отклики	Наблюдение
	1	2	3	4	5
	0	0,5	1,0	1,5	2,0	5
	7,0	4,8	2,8	1,4	0	16
	0	2,4	2,8	2,1	0	7,3

Решение

Примем, что кроме управляемого фактора при проведении эксперимента на объект воздействует случайный фактор, распределенный по нормальному закону с математическим ожиданием . Также предположим, что эта связь - линейная, следовательно, уравнение регрессии нужно определять в виде:

Неизвестных коэффициентов два: и . Запишем (5.3) в виде двух уравнений для и в каждом из них разложим суммы по индексу :

Так как , получим:

Подставим данные эксперимента из табл. 5.10 в систему (5.4):

Решим систему из двух уравнений и получим: , .

Следовательно, искомое уравнение регрессии:

Доверительные границы для истинных значений и примера 5.8 определяются как обычно:

где - аргумент распределения Стьюдента; - среднеквадратические отклонения величин и соответственно.

Значения определяются из таблицы распределения Стьюдента для степеней свободы и задаваемом уровне достоверности . Пусть , тогда .

Значения находятся по формулам:

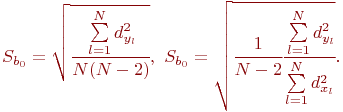
Данные для вычисления , представлены в табл. 5.11.

Таблица 5.11. Данные для вычисления S_b0, S_b1

1	0	1,0	1,0	7,0	6,68	-0,32	0,1024
2	0,5	0,5	0,25	4,8	4,94	0,14	0,0196
3	1,0	0	0	2,8	3,2	0,40	0,16
4	1,5	-0,5	0,25	1,4	1,46	0,06	0,0036
5	2,0	-1,0	1,0	0	0,28	0,28	0,0784

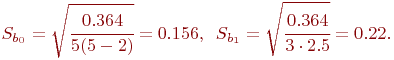
С уровнем достоверности

Большой размах доверительных границ объясняется малым числом наблюдений в данном эксперименте.

Доверительные границы для y принимают разные значения в зависимости от значений факторов [33].

На практике часто ограничиваются обобщенными оценками адекватности построенной модели: величиной среднего абсолютного отклонения

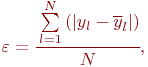
или (и) величиной среднеквадратической ошибки на единицу веса

Весом или степенью свободы эксперимента называют разность между числом наблюдений и числом коэффициентов регрессии

Предположим, что линейная модель недостаточно точно отображает связь между фактором и откликом .

Введем в рассмотрение более сложную нелинейную модель:

Для определения коэффициентов регрессии обозначим и получим двухфакторную линейную модель:

В этом случае уравнение (5.3) раскрывается так:

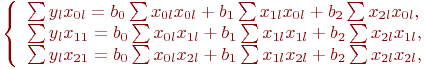
В уравнениях принято:

Так как , , то система принимает вид:

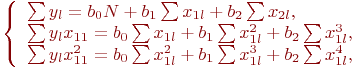
Подставим значения фактора и отклика из табл. 5.10:

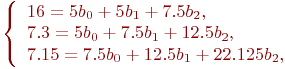
Решим систему из трех уравнений с тремя неизвестными и получим: .

Таким образом, получено новое уравнение регрессии:

По значениям и нетрудно убедиться в том, что нелинейная модель более точно отображает моделируемый процесс (см. табл. 5.10), чем линейная.

В рассмотренном примере ошибка модели определялась по тем же данным, по которым и была определена сама модель. Однако при сокращенных планах экспериментов (см. п. 4.3) можно выполнить все или часть "сэкономленных" наблюдений для получения так называемых проверочных данных, которые и использовать для вычисления ошибки или . В этом случае оценка адекватности модели будет более объективна, хотя число наблюдений в эксперименте увеличивается, и экономии их не будет.

По уравнению регрессии можно сделать ориентировочную оценку чувствительности отклика к изменению того или иного фактора. Например, в уравнении влияние фактора на отклик незначительно по сравнению с другими, так как коэффициент намного меньше остальных коэффициентов.

В программном пакете MS Excel есть функция "Регрессия", которая может выполнить всесторонний регрессионный анализ данных компьютерного эксперимента.

Пример 5.9. В ремонтное подразделение поступают вышедшие из строя средства связи (СС) с интервалами времени, подчиненными показательному закону с математическим ожиданием . В каждом СС могут быть неисправными в любом сочетании блоки A, B, C с вероятностями , , соответственно. Ремонтное подразделение ремонтирует СС путем замены неисправных блоков исправными блоками. В момент поступления неисправного СС в ремонтное подразделение вероятности наличия в нем исправных блоков соответственно . Наличие и замена блока обязательно при любом сочетании неисправных блоков.

Построить имитационную модель "Система ремонта" с целью определения вероятности ремонта СС с неисправными блоками , и , , за время . По результатам эксперимента получить уравнение регрессии, связывающее вероятность ремонта СС с вероятностями .

Решение

Постановка примера 5.9 аналогична постановке примера 3.8. Отличие состоит в том, что введен фактор времени - интервалы поступления неисправных СС. Это учтено в модели, при разработке которой использовался алгоритм примера 3.8 (см. рис. 3.18).

Для построения уравнения регрессии введем обозначения:

- отклик модели, вероятность ремонта СС с неисправными блоками и за время ;

- фактор, представляющий вероятность ;

- фактор, представляющий вероятность ;

- фактор, представляющий вероятность ;

- фактор, представляющий вероятность ;

- фактор, представляющий вероятность .

Исходные данные и результаты эксперимента с моделью в количестве 32 наблюдений приведены в табл. 5.12. По этим данным функция "Регрессия" из MS Excel сформировала искомое уравнение:

Таблица 5.12. Результаты эксперимента с моделью "Система ремонта"

№ отклика
1	0,088	0,3	0,55	0,5	0,2	0,65
2	0,127	0,3	0,55	0,5	0,2	0,95
3	0,303	0,3	0,55	0,5	0,8	0,65
4	0,442	0,3	0,55	0,5	0,8	0,95
5	0,099	0,3	0,55	0,9	0,2	0,65
6	0,146	0,3	0,55	0,9	0,2	0,95
7	0,317	0,3	0,55	0,9	0,8	0,65
8	0,46	0,3	0,55	0,9	0,8	0,95
9	0,116	0,3	0,85	0,5	0,2	0,65
10	0,167	0,3	0,85	0,5	0,2	0,95
11	0,445	0,3	0,85	0,5	0,8	0,65
12	0,653	0,3	0,85	0,5	0,8	0,95
13	0,12	0,3	0,85	0,9	0,2	0,65
14	0,175	0,3	0,85	0,9	0,2	0,95
15	0,452	0,3	0,85	0,9	0,8	0,65
16	0,66	0,3	0,85	0,9	0,8	0,95
17	0,118	0,3	0,55	0,5	0,2	0,65
18	0,173	0,9	0,55	0,5	0,2	0,95
19	0,336	0,9	0,55	0,5	0,8	0,65
20	0,486	0,9	0,55	0,5	0,8	0,95
21	0,158	0,9	0,55	0,9	0,2	0,65
22	0,228	0,9	0,55	0,9	0,2	0,95
23	0,373	0,9	0,55	0,9	0,8	0,65
24	0,544	0,9	0,55	0,9	0,8	0,95
25	0,127	0,9	0,85	0,5	0,2	0,65
26	0,184	0,9	0,85	0,5	0,2	0,95
27	0,457	0,9	0,85	0,5	0,8	0,65
28	0,67	0,9	0,85	0,5	0,8	0,95
29	0,137	0,9	0,85	0,9	0,2	0,65
30	0,201	0,9	0,85	0,9	0,2	0,95
31	0,471	0,9	0,85	0,9	0,8	0,65
32	0,689	0,9	0,85	0,9	0,8	0,95

Кроме вычисленных оценок коэффициентов регрессии функция "Регрессия" выдает также результаты регрессионного анализа (табл. 5.13): вычисленные значения откликов , разность между ними и измеренными в эксперименте в каждом наблюдении , среднеквадратические ошибки в определении коэффициентов регрессии и откликов при определенных значениях факторов и некоторые другие.

Таблица 5.13. Результаты регрессионного анализа

	Коэффициенты	Стандартная ошибка	t-статистика
-пересечение	-0,52287	0,083821	-6,23787
Переменная	0,044568	0,034409	1,295248
Переменная	0,270679	0,068279	3,964334
Переменная	0,048634	0,051209	0,949722
Переменная	0,559089	0,034139	16,37673
Переменная	0,387762	0,068279	5,679123
Наблюдение	Предсказанное Y	Остатки	Стандартные остатки
1	0,027558	0,060442	1,141425
2	0,143886	-0,01689	-0,31889
3	0,363011	-0,06001	-1,13329
4	0,47934	-0,03734	-0,70515
5	0,047011	0,051989	0,981781
6	0,16334	-0,01734	-0,32746
7	0,382465	-0,06547	-1,23628
8	0,498794	-0,03879	-0,7326
9	0,108761	0,007239	0,136697
10	0,22509	-0,05809	-1,09701
11	0,444215	0,000785	0,014822
12	0,560544	0,092456	1,745995
13	0,128215	-0,00822	-0,15514
14	0,244544	-0,06954	-1,31331
15	0,463669	-0,01167	-0,22036
16	0,579998	0,080002	1,510813
17	0,027558	0,090442	1,707963
18	0,170627	0,002373	0,044804
19	0,389752	-0,05375	-1,01509
20	0,506081	-0,02008	-0,37922
21	0,073752	0,084248	1,590978
22	0,190081	0,037919	0,716081
23	0,409206	-0,03621	-0,68374
24	0,525535	0,018465	0,348706
25	0,135502	-0,00850	-0,16057
26	0,251831	-0,06783	-1,28096
27	0,470956	-0,01396	-0,26356
28	0,587285	0,082715	1,56204
29	0,154956	-0,01796	-0,33909
30	0,271285	-0,07028	-1,3273
31	0,490410	-0,01941	-0,36655
32	0,606739	0,082261	1,553472

Пример 5.10. На узел связи поступают заявки на передачу сообщений. Интервалы времени поступления заявок подчинены показательному закону с математическим ожиданием . На узле связи имеются два канала передачи данных. При поступлении очередной заявки в интервале времени вероятности того, что каналы и будут свободны, соответственно равны и . При поступлении заявок после времени вероятности того, что каналы и будут свободны, соответственно равны и . Сообщение передаётся по любому свободному каналу. Если оба канала заняты, заявка теряется.

Построить имитационную модель "Обработка запросов на узле связи" с целью определения абсолютного и относительного числа потерянных заявок из их общего количества, поступивших на узел связи за время , . Получить уравнение регрессии, связывающее относительную долю обслуженных заявок с интервалами их поступления и вероятностями

Решение

Имитационная модель построена в соответствии с алгоритмом (см. рис. 3.21). Для построения уравнения регрессии введем обозначения:

- отклик модели, вероятность ремонта СС с неисправными блоками , и , , за время ;

- фактор, представляющий вероятность ;

- фактор, представляющий вероятность ;

- фактор, представляющий вероятность ;

- фактор, представляющий вероятность ;

- фактор, представляющий интервалы поступления заявок .

Исходные данные и результаты эксперимента приведены в табл. 5.14. Для регрессионного анализа также использовалась функция "Регрессия" MS Excel. Получено искомое уравнение:

Таблица 5.14. Результаты эксперимента с моделью "Обработка запросов на узле связи"

Номер отклика
1	0,405	0,5	0,7	0,3	0,3	1
2	0,406	0,5	0,7	0,3	0,3	9
3	0,09	0,5	0,7	0,3	0,9	1
4	0,09	0,5	0,7	0,3	0,9	9
5	0,195	0,5	0,7	0,7	0,3	1
6	0,195	0,5	0,7	0,7	0,3	9
7	0,06	0,5	0,7	0,7	0,9	1
8	0,06	0,5	0,7	0,7	0,9	9
9	0,38	0,5	0,9	0,3	0,3	1
10	0,38	0,5	0,9	0,3	0,3	9
11	0,65	0,5	0,9	0,3	0,9	1
12	0,65	0,5	0,9	0,3	0,9	9
13	0,17	0,5	0,9	0,7	0,3	1
14	0,17	0,5	0,9	0,7	0,3	9
15	0,035	0,5	0,9	0,7	0,9	1
16	0,0348	0,5	0,9	0,7	0,9	9
17	0,375	0,9	0,7	0,3	0,3	1
18	0,376	0,9	0,7	0,3	0,3	9
19	0,06	0,9	0,7	0,3	0,9	1
20	0,06	0,9	0,7	0,3	0,9	9
21	0,165	0,9	0,7	0,7	0,3	1
22	0,165	0,9	0,7	0,7	0,3	9
23	0,03	0,9	0,7	0,7	0,9	1
24	0,0301	0,9	0,7	0,7	0,9	9
25	0,37	0,9	0,9	0,3	0,3	1
26	0,37	0,9	0,9	0,3	0,3	9
27	0,055	0,9	0,9	0,3	0,9	1
28	0,055	0,9	0,9	0,3	0,9	9
29	0,16	0,9	0,9	0,7	0,3	1
30	0,16	0,9	0,9	0,7	0,3	9
31	0,025	0,9	0,9	0,7	0,9	1
32	0,025	0,9	0,9	0,7	0,9	9

Результаты регрессионного анализа, аналогичные рассмотренным в примере 5.9 (табл. 5.13), приведены в табл. 5.15.

Таблица 5.15. Результаты регрессионного анализа

	Коэффициенты	Стандартная ошибка	t-статистика
-пересечение	0,526135	0,211881	2,483165
Переменная	-0,23277	0,112257	-2,0735
Переменная	0,289906	0,224514	1,291259
Переменная	-0,48314	0,112257	-4,30387
Переменная	-0,25334	0,074838	-3,38522
Переменная	1,48E-05	0,005613	0,002645
Наблюдение	Предсказанное Y	Остатки	Стандартные остатки
1	0,391756	0,013244	0,113864
2	0,391875	0,014125	0,12144
3	0,23975	-0,14975	-1,28748
4	0,239869	-0,14987	-1,2885
5	0,1985	-0,0035	-0,03009
6	0,198619	-0,00362	-0,03111
7	0,046494	0,013506	0,116121
8	0,046613	0,013387	0,1151
9	0,449738	-0,06974	-0,59957
10	0,449856	-0,06986	-0,60059
11	0,297731	0,352269	3,02865
12	0,29785	0,35215	3,027629
13	0,256481	-0,08648	-0,74353
14	0,2566	-0,0866	-0,74455
15	0,104475	-0,06948	-0,59732
16	0,104594	-0,06979	-0,60006
17	0,29865	0,07635	0,656423
18	0,298769	0,077231	0,664
19	0,146644	-0,08664	-0,74492
20	0,146763	-0,08676	-0,74595
21	0,105394	0,059606	0,512468
22	0,105513	0,059487	0,511447
23	-0,04661	0,076612	0,65868
24	-0,04649	0,076594	0,658519
25	0,356631	0,013369	0,114939
26	0,35675	0,01325	0,113918
27	0,204625	-0,14963	-1,28641
28	0,204744	-0,14974	-1,28743
29	0,163375	-0,00338	-0,02902
30	0,163494	-0,00349	-0,03004
31	0,011369	0,013631	0,117195
32	0,011488	0,013512	0,116174

Вопросы для самоконтроля

1. Что понимают под характеристикой случайных величин и процессов?
2. Что такое несмещенная оценка характеристики случайной величины? Состоятельная? Эффективная?
3. Что характеризует гистограмма? Правило построения гистограммы.
4. В чем состоит сущность дисперсионного анализа?
5. Что такое ошибки первого рода и второго рода при оценке гипотез?
6. Что такое F - распределение и почему оно является мерой сравнения дисперсий случайных величин?
7. Для чего используется критерий Вилькоксона?
8. В чем состоит методика выявления несущественных факторов?
9. Назначение корреляционного анализа.
10. Назначение регрессионного анализа.
11. Представьте графически виды корреляции между двумя переменными.
12. Составьте систему уравнений для определения коэффициентов регрессии модели вида:
    
13. Для линейной и нелинейной моделей, полученных в п. 5.12, вычислить и сравнить ошибки и .
14. С объектом проведено экспериментов. Данные экспериментов приведены в таблице:

    Измерения	Эксперименты
    	1	2	3	4	5	6
    	2	1	4	3	6	5
    	3	2	5	4	8	7

    Построить линейную математическую модель функционирования объекта вида: . Расчеты провести в таблице. Проверьте адекватность модели при абсолютной точности 0,2.

    Ссылки

    Боев В.Д., Сыпченко Р.П. Компьютерное моделирование

    оглавление   ДМ   экономическая информатика   визуальные среды - 4GL   Теория и практика обработки информации
    
    
    Знаете ли Вы, что синтетические модели - это математические модели, разрабатываемые для проектирования новых, отличающихся от известных, систем с заданными свойствами. К числу синтетических экономико-математических моделей относятся, например, модели машинно-тракторного парка, модели формирования инвестиционных программ и др.

    НОВОСТИ ФОРУМА Рыцари теории эфира

    10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров. 10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров. 10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров. 10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров. 10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров. 10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров. 10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров. 10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров. 10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров. 10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.