оглавление ДМ экономическая информатика визуальные среды - 4GL Теория и практика обработки информации

Пакеты линейной алгебры и функциональных систем

Основные определения линейной алгебры
Пакет решения задач линейной алгебры linatg
Состав пакета linalg
Интерактивный ввод матриц
Основные функции для задания векторов и матриц
Функции для работы, с векторами и матрицами
Решение систем линейных уравнений.
Пакет линейной алгебры с алгоритмами NAG LinearAlgebra
Назначение и загрузка пакета LinearAlgebra.
Примеры матричных операций с применением пакета LinearAlgebra
Интеграция Maple 7 с MATLAB
Краткие сведения о MATLAB
Загрузка пакета расширения Matlab
Типовые матричные операции пакета расширения Matlab
Выделение сигнала на фоне шумов
Пакет анализа линейных функциональных систем LinearFunctionalSystems
Назначение пакета LinearFunctionalSystems
Тестовые функции пакета LinearFunctionalSystems
Функции решения линейных функциональных систем
Вспомогательные функции
Примеры применения пакета LinearFunctiftnalSystems
Что нового мы узнали?

Основные определения линейной алгебры

Прежде чем перейти к рассмотрению обширных возможностей пакетов Maple 7 по части решения задач линейной алгебры, рассмотрим краткие определения, относящиеся к ней.

Матрица (m х n) — прямоугольная двумерная таблица, содержащая m строк и n столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы).

Квадратная матрица — матрица, у которой число строк m равно числу столбцов n. Пример квадратной матрицы размера 3x3:

Сингулярная (вырожденная) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.

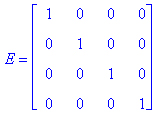
Единичная матрица — это квадратная матрица, у которой диагональные элементы равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размера 4x4:

Сингулярные значения матрицы А — квадратные корни из собственных значений матрицы А^Т=А, где А^т - транспонированная матрица А (см. ее определение ниже);Транспонированная матрица — матрица, у которой .столбцы и строки меняются . местами, то есть элементы транспонированной матрицы удовлетворяют условию A^T(i,j)=A(j,i). Приведем простой пример. Исходная матрица:

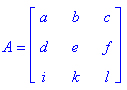
Транспонированная матрица:

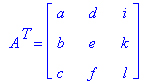
Обратная матрица — это матрица М^-1, которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е.

Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули.

Диагональ матрицы — расположенные диагонально элементы A_i,i матрицы А. В приведенной ниже матрице элементы диагонали представлены заглавными буквами:

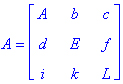
Обычно указанную диагональ называют главной диагональю — для матрицы А, приведенной выше, это диагональ с элементами А, Е и L. Иногда вводят понятия под диагоналей (элементы d и k) и над диагоналей (элементы b и f). Матрица, все элементы которой, расположенные кроме как на диагонали, под диагонали и над диагонали, равны нулю, называется ленточной.

Ранг матрицы — наибольший из порядков отличных от нуля миноров квадратной матрицы.

След матрицы — сумма диагональных элементов матрицы.

Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением n элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:

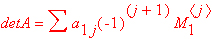
где M₁^<j> — определитель матрицы порядка n - 1, полученной из матрицы А вычеркиванием первой строки и j-гo столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.

Матрица в целой степени — квадратная матрица в степени n (n — целое неотрицательное число), определяемая следующим образом:

М° = Е, М¹ = М, М² = ММ ..., Мⁿ =М^n-1М.

Идемпотентная матрица — матрица, отвечающая условию Р² = Р.

Симметрическая матрица — матрица, отвечающая условию А^т = А.

Кососимметрическая матрица — матрица, отвечающая условию А^т = -A. Ортогональная матрица — матрица, отвечающая условию А^т =А^-1.Нуль-матрица — матрица, все элементы которой равны 0.Блок-матрица — матрица, составленная из меньших по размеру матриц, также можно представить как матрицу, каждый элемент которой — матрица. Частным случаем является блок-диагональная матрица — блок-матрица, элементы-матрицы которой вне диагонали — нуль-матрицы.

Комплексно-сопряженная матрица — матрица А, полученная из исходной матрицы А заменой ее элементов на комплексно-сопряженные. Эрмитова матрица — матрица А, удовлетворяющая условию А = А .Собственный вектор квадратной матрицы А — любой вектор х е V", х* О, удовлетворяющий уравнению Ах = gx, где g — некоторое число, называемое собственным значением матрицы А.

Характеристический многочлен матрицы — определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена, — |А - gE|. Собственные значения матрицы — корни ее характеристического многочлена. Норма — обобщенное понятие абсолютной (величины числа. Норма трехмерного вектора ||х|| — его длина. Норма матрицы — значение sup(||Ax||/||x||).

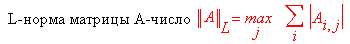
Матричная форма записи системы линейных уравнений — выражение АХ = В, где А — матрица коэффициентов системы, X — вектор неизвестных и В — вектор свободных членов. Один из способов решения такой системы очевиден — X = А^-1В, где А^-1 — обратная матрица.

Пакет решения задач линейной алгебры linalg

Состав пакета linalg

Несомненно, что уникальной возможностью системы Maple 7, как и других систем компьютерной алгебры, является возможность решения задач линейной алгебры в символьном (формульном, аналитическом) виде. Однако такое решение представляет скорее теоретический, чем практический интерес, поскольку даже при небольших размерах матриц (уже при 4-5 строках и столбцах) символьные результаты оказываются очень громоздкими и труднообозримыми. Они полезны только при решении специфических аналитических задач, например с разреженными матрицами, у которых большинство элементов имеют нулевые значения.

Поэтому разработчики Maple 7 были вынуждены реализовать в своей системе численные методы решения задач линейной алгебры, которые широко используются в основных сферах ее приложения — математическом моделировании систем и устройств, расчетах в электротехнике, механике, астрономии и т. д.

В ядро Maple 7, как отмечалось, введены очень скромные и минимально необходимые средства для решения задач линейной алгебры. Основной упор в их реализации сделан на подключаемые пакеты. Основным из них, унаследованным от предшествующих реализаций системы, является пакет решения задач линейной алгебры Unalg. Это один из самых обширных и мощных пакетов в области решения задач линейной алгебры. Он содержит свыше ста функций:

> with(linalg);

Warning, the names fibonacci, inverse and multiply have been redefined Warning, the protected names norm and trace have been redefined and unprotected[BlockDiagonal, GramSchmidt, JordanBlock, LUdecomp, QRdecomp, Wronskian, addcol, addrow, adj, adjoint, angle, augment, backsub, band, basis, bezout, blockmatrix, charmat, charpoly, cholesky, col, coldim, colspace, colspan, companion, concat, cond, copyinto, crossprod, curl, definite, delcols, delrows, det, diag, diverge, dotprod, eigenvals, eigenvalues, eigenvectors, eigenvects, entermatrix, equal, exponential, extend, ffgausselimfifibonacci,forwardsub,frobenius, gausselim, gaussjord, geneqns, genmatrix, grad, hadamard, hermite, hessian, hilbert,htranspose, thermite, indexfunc, innerprod, intbasis, inverse, ismith, issimilar, iszerojacobian, Jordan, kernel, laplacian, leastsqrs, linsolve,matadd, matrix, minor, minpoly, mulcol, /им/row,multiply, norm, normalize, nullspace, orthog, permanent, pivot, potential, randmatrix, randvector, rank, ratform, row, rowdim, rowspace, rowspan, rref, scalarmul, singularvals, smith, stackmatrix, submatrix, subvector, sumbasis, swapcol, swaprow, Sylvester, toeplitz, trace, transpose, vandermonde, vecpotent, vectdim, vector, wronskian]

Ниже указано назначение тех функций пакета linalg, которые подробно не описаны:

addcol — добавляет к одному из столбцов другой столбец, умноженный на некоторое число;
addrow — добавляет к одной из строк другую строку, умноженную на некоторое число;
angle — вычисляет угол между векторами;
augment — объединяет две или больше матриц по горизонтали;
backsub — реализует метод обратной подстановки при решении системы линейных уравнений (см. также forwardsub);
band — создает ленточную матрицу;
basis — находит базис векторного пространства;
bezout — создает Bezout-матрицу двух полиномов; . _г
BlockDiagonal — создает блок-диагональную матрицу;
blockmatrix — создает блок-матрицу;
cholesky — декомпозиция Холесского для квадратной положительно определенной матрицы;
charmat — создает характеристическую матрицу (charmat(M,v) — матрица, вычисляемая как v E-M);
charpoly — возвращает характеристический полином матрицы;
colspace — вычисляет базис пространства столбцов;
colspan — находит базис линейной оболочки столбцов матрицы;
companion — вычисляет сопровождающую матрицу, ассоциированную с полиномом;
cond — вычисляет число обусловленности матрицы (cond(M) есть величина norm(M) norm(М^-1);
curl — вычисляет ротор вектора;
definite — тест на положительную (отрицательную) определенность матрицы;
diag — создает блок-диагональную матрицу;
diverge — вычисляет дивергенцию векторной функции;
eigenvals — вычисляет собственные значения матрицы;
eigenvects — вычисляет собственные векторы матрицы;
equal — определяет, являются ли две матрицы равными;
exponential — создает экспоненциальную матрицу;
ffgausselim — свободное от дробей Гауссово исключение в матрице;
fibonacci — матрица Фибоначчи;
forwardsub — реализует метод прямой подстановки при решении системы линейных уравнений (например, для матрицы L и вектора b
forwardsub(L, b) возвращает вектор решения х системы линейных уравнений L-x=b);
frobenius — вычисляет форму Фробениуса (Frobenius) матрицы;
gausselim — Гауссово исключение в матрице;
gaussjord — синоним для rref (метод исключения Гаусса—Жордана);
geneqns — генерирует элементы матрицы из уравнений;
genmatrix — генерирует матрицу из коэффициентов уравнений;
grad — градиент векторного выражения;
GramSchmidt — вычисляет ортогональные векторы;
hadamard — вычисляет ограничение на коэффициенты детерминанта;
hessian — вычисляет гессиан-матрицу выражения;
hilbert — создает матрицу Гильберта;
htranspose — находит эрмитову транспонированную матрицу;
ihermite — целочисленная эрмитова нормальная форма;
indexfunc — определяет функцию индексации массива;
Innerprod — вычисляет векторное произведение;
Intbasis — определяет базис пересечения пространств;
ismith — целочисленная нормальная форма Шмитта;
iszero — проверяет, является ли матрица ноль-матрицей;
jacobian —' вычисляет якобиан векторной функции;
JordanBlock — возвращает блок-матрицу Жордана;
kernel — находит базис ядра преобразования, соответствующего данной матрице;
laplacian — вычисляет лапласиан;
leastsqrs — решение уравнений по методу наименьших квадратов;
linsolve — решение линейных уравнений;
LudeComp — осуществляет LU-разложение;
minpoly — вычисляет минимальный полином матрицы;
mulcol — умножает столбец матрицы на заданное выражение;
mulrow — умножает строку матрицы на заданное выражение;
multiply — перемножение 'матриц или матрицы и вектора;
normalize — нормализация вектора;
orthog — тест на ортогональность матрицы;
permanent — вычисляет перманент матрицы — определитель, вычисляемый без перестановок;
pivot — вращение относительно элементов матрицы;
potential — вычисляет потенциал векторного поля;
Qrdecomp — осуществляет QR-разложение;
randmatrix — генерирует случайные матрицы;
randvector — генерирует случайные векторы;
ratform — вычисляет рациональную каноническую форму;
references — выводит список основополагающих работ по линейной алгебре;
rowspace — вычисляет базис пространства строки;
rowspan — вычисляет векторы охвата для места столбца;
rref — реализует преобразование Гаусса-Жордана матрицы;
scalarmul — умножение матрицы или вектора на заданное выражение;
singval — вычисляет сингулярное значение квадратной матрицы;
singularvals — возвращает список сингулярных значений квадратной матрицы;
smith — вычисляет Шмиттову нормальную форму матрицы;
submatrix — извлекает указанную подматрицу из матрицы;
subvector — извлекает указанный вектор из матрицы;
sumbasis — определяет базис объединения системы векторов;
swapcol — меняет местами два столбца в матрице;
swaprow — меняет местами две строки в матрице;
sylvester — создает матрицу Сильвестра из двух полиномов;
toeplitz — создает матрицу Теплица;
trace — возвращает след матрицы;
vandermonde — создает вандермондову матрицу;
vecpotent — вычисляет векторный потенциал;
vectdim — определяет размерность вектора;
wronskian — вронскиан векторных функций.

Ниже мы рассмотрим более подробно наиболее часто используемые функции из этого пакета. С деталями синтаксиса (достаточно разнообразного) для каждой из указанных функций можно ознакомиться в справочной системе Maple. Для этого достаточно использовать команду

?name; где name — имя функции (из приведенного списка).

Интерактивный ввод матриц

Для интерактивного ввода матриц можно, определив размерность некоторого массива, использовать функцию entermatrix:

> А:=аггау(1..3,1..3):

А :=аггау(1 ..3,1 .. 3, [ ])

После исполнения этого фрагмента документа диалог с пользователем имеет следующий вид:

Основные функции для задания векторов и матриц

В библиотечном файле Unalg имеются следующие функции для задания векторов и матриц:

vector(n,list) — сoздание вектора с n элементами, заданными в списке list;
matrix(n,m,list) — создание матрицы с числом строк n и столбцов m с элементами, заданными списком list.

Ниже показано применение этих функций:

Обратите внимание на последние примеры — они показывают вызов индексированных переменных вектора и матрицы.

Функции для работы с векторами и матрицами

Для работы с векторами и матрицами Maple 7 имеет множество функций, входящих в пакет linalg. Ограничимся приведением краткого описания наиболее распространенных функций этой категории.

Операции со структурой отдельного вектора V и матрицы М:

coldim(M) — возвращает число столбцов матрицы М;
rowdim(M) — возвращает число строк матрицы М;
vectdim(V) — возвращает размерность вектора V;
col(M,i) — возвращает i-й столбец матрицы М;
row(M,i) — возвращает i-ю строку матрицы М;
tninor(M,i, j) — возвращает минор матрицы М для элемента с индексами i и j;
delcols(M,i.. j) — удаляет столбцы матрицы М от i-roдо j-ro;
del rows (V,i..j) — удаляет строки матрицы М от i-й до j-й;
extend (М, т, n,х) — расширяет матрицу М на m строк и n столбцов с применением заполнителя х.

Основные векторные и матричные операции:

dotprod(U,V) — возвращает скалярное произведение векторов U и V;
crossprod(U,V) — возвращает векторное произведение векторов U и V;
norm(V) или norm(M) — возвращает норму вектора или матрицы;
copyinto(A,B,i, j) — копирует матрицу А в В для элементов последовательно от i до j;
concat(Ml,M2) — возвращает объединенную матрицу с горизонтальным слиянием матриц Ml и М2;
stack(Ml,M2) — возвращает объединенную матрицу с вертикальным слиянием Ml и М2;
matadd(A,B) и evalm(A+B) — возвращает сумму матриц А и В;
multlply(A,B) и evalm(A&*B) — возвращает произведение матриц А и В;
adjoint (М) или adj(M) — возвращает присоединенную матрицу, такую что M?adj(M) дает диагональную матрицу, определитель которой есть det(M);
charpoly(M,lambda) — возвращает характеристический полином матрицы М относительно заданной переменной lambda;
det(M) — возвращает детерминант (определитель) матрицы М;
Eigenvals(M,vector) — инертная форма функции, возвращающей собственные значения матрицы М и (при указании необязательного параметра vector) соответствующие им собственные векторы;
jordan(M) — возвращает матрицу М в форме Жордана;
hermite(M) — возвращает матрицу М в эрмитовой форме;
trace(M) — возвращает след матрицы М;
rank(M) — возвращает ранг матрицы М;
transpose(M) — возвращает транспонированную матрицу М;
inverse(M) или evalm(l/M) — возвращает матрицу, обратную к М;
singularvals(A) — возвращает сингулярные значения массива или матрицы А.

Приведем примеры применения некоторых из этих функций:

Читатель, понимающий суть матричных вычислений, легко справится с тестированием других функций, входящих в пакет linalg. В приведенных примерах полезно обратить внимание на то, что многие матричные функции способны выдавать результаты вычислений в аналитическом виде, что облегчает разбор выполняемых ими операций.

Решение систем линейных уравнений

Ниже представлен простой пример составления и решения трех систем линейных уравнений с применением функций, входящих в пакет linalg:

А теперь рассмотрим пример решения матричного уравнения в символьном виде:

Следующий пример показывает решение более сложной системы линейных уравнений с комплексными коэффициентами:

На этот раз решение получено использованием функций умножения матриц и вычисления обратной матрицы в виде X = А-¹ В, то есть в матричном виде. В конце примера показано преобразование результатов с целью их получения в обычной форме комплексных чисел с частями, представленными в форме чисел с плавающей точкой.

Пакет линейной алгебры с алгоритмами NAG LinearAlgebra

Назначение и загрузка пакета LinearAlgebra

В последние годы разработчики систем символьной математики осознали, что малая скорость выполнения векторных и матричных операций при решении задач линейной алгебры оборачивается потерей заметной части рынка систем компьютерной математики. Новые версии таких систем (Mathematica 4/4.1 и Maple 6/7) отличаются от прежних прежде всего резким повышением эффективности решения задач линейной алгебры в численном виде.

В новых реализациях систем Maple и MATLAB была сделана ставка на использование давно апробированных быстрых алгоритмов линейной алгебры, предложенных создателями Number Algorithm Group (NAG). Эти алгоритмы издавна применяются на больших ЭВМ и суперкомпьютерах, обеспечивая ускорение численных матричных операций от нескольких раз до нескольких десятков раз. Их применение обеспечивает эффективное использование систем символьной математики в решении задач, сводящихся к задачам линейной алгебры. В числе таких задач многочисленные задачи теоретической электротехники, механики многих объектов, моделирования электронных устройств и т. д. В Maple 7 использование алгоритмов NAG является одной из первых отличительных черт новой версии системы. Оно реализуется новым пакетом LinearAlgebra. Для его загрузки используются следующие команды:

> restart; with(LinearAlgebra):

[Add, Adjoint, BackwardSubstitute, BandMatrix, Basis, BezoutMatrix, BidiagonalForm, BilinearForm, CharacteristicMatrix, CharacteristicPolyhomial, Column, ColumnDimension, ColumnOpemtion, ColumnSpace, CompanionMatrix, CondittonNumber, ConstantMatrix, ConstantVector, CreatePermutation, CrossProduct, DeleteColumn, DeleteRow, Determinant, DiagonalMatrix, Dimension,

Dimensions, DotProduct, Eigenvalues, Eigenvectors, Equql, FonyardSubstitute, FrobeniusForm, GenerateEquations, GenerateMatrix, GetResuNDataType, * GetResultShape, GivensRotationMatrix, GramSchmidt, HarikelMatrix, HermiteForm, HermitianTranspose, HessenbergForm, HilbertMatrix, Households-Matrix, IdentityMatrix, IntersectionBasis, IsDefinite, IsOrthogonal, IsSimilar, IsUnitary,

JordanBlockMatrix, JordanForm, LA_Main, LUDecomposition, LeastSquares, LinearSolve, Map, Map2, MatrixAdd, Matrixlnverse, MatrixMatrixMultiply, MatrixNorm, MatrixScalarMultiply, MatrixVectorMultiply,Minimal/Polynomial, Minor, Multiply, NoUserValue, Norm, Normalize, NullSpace, OuterProductMatrix, Permanent, Pivot, QRDecomposition, RandomMatrix, RandomVector, Rank, Row,

RowDimension, RowOperation, RowSpace, ScalarMatrix, ScalarMultiply, ScalarVector, SchurForm, SingularValues, SmithForm, SubMatrix, SubVector, SumBasis, SylvesterMatrix, ToeplitzMatrix, Trace, Transpose, TridiagonalForm, UnitVector, VandermondeMatrix, VectorAdd, VectorAngle, VectorMatrixMultiply, VectorNorm, VectorScalarMultiply, ZeroMatrix, Zero Vector, Zip ]

> 1nfolevel[LinearA1gebra]:=l:

infolevel_{LinearAlgebra}:=1

Нетрудно заметить, что многие функции этого пакета повторяет по назначению функции более старого пакета linalg, описанного выше. Поэтому мы не будем останавливаться на их повторном описании. Главное то, что эти функции задействуют возможности быстрых алгоритмов NAG и в отличие от функций пакета linalg ориентированы на численные расчеты в формате обработки вещественных чисел, характерном для компьютерной платформы. Знающий матричные методы читатель легко поймет назначение функций пакета LinearAlgebra по их составным названиям. Например, DeleteColumn означает удаление столбца матрицы, ToeplitzMatrix означает создание матрицы Теплица, ZeroMatrix — создание матрицы с нулевыми элементами и т. д. Все имена функций этого пакета начинаются с заглавной буквы.

Примеры матричных операций с применением пакета LinearAlgebra

Применение алгоритмов NAG особенно эффективно в том случае, когда используется встроенная в современные микропроцессоры арифметика чисел с плавающей запятой. С помощью специального флага такую арифметику можно отключать или включать:

> UseHardwareFloats := false; # use software floats

UseHardwareFloats :=false

> UseHardwareFloats := true: # default behaviour

UseHardwareFloats :=true

Матрицы в новом пакете линейной алгебры могут задаваться в угловых скобках, как показано ниже:

После этого можно выполнять с ними типовые матричные операции. Например, можно инвертировать (обращать) матрицы:

Обратите внимание, что Maple 7 теперь выдает информационные сообщения о новых условиях реализации операции инвертирования матриц с вещественными элементами, и в частности об использовании алгоритмов NAG и арифметики, встроенной в сопроцессор. ₍

Следующий пример иллюстрирует создание двух случайных матриц Ml и М2 и затем их умножение:

Параметр inplace в функции умножения обеспечивает помещение результата умножения матриц на место исходной матрицы Ml — излюбленный прием создателей быстрых матричных алгоритмов NAG. Поскольку матрицы Ml и М2 за- -даны как случайные, то при повторении этого примера результаты, естественно, будут иными, чем приведенные.

Следующий пример иллюстрирует проведение хорошо известной операции/ LU-разложения над матрицей М, созданной функцией Matrix:

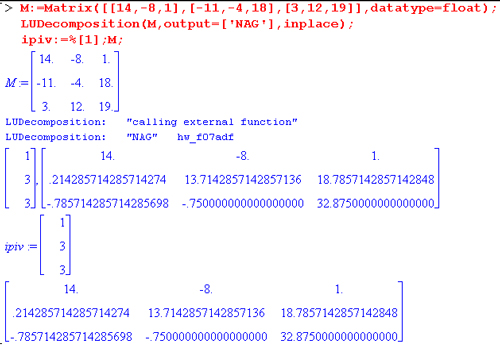
Конечной целью большинства матричных операций является решение систем линейных уравнений. Для этого пакет LinearAlgebra предлагает великое множество методов и средств их реализации. Мы ограничимся простым примером одновременного решения сразу трех систем уравнений. Дабы не загромождать книгу массивными выражениями, ограничимся решением систем из двух линейных уравнений, матрица коэффициентов у которых одна, а векторы свободных членов разные. Ниже показан пример решения такой системы:

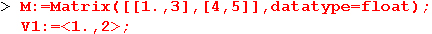
На этом, учитывая ограниченный объем книги, мы завершаем обзор пакета LmearAlgebra. Читатель, познающий или знающий методы линейной алгебры, может опробовать в работе любые функции этого пакета самостоятельно или познакомиться со множеством примеров, размещенных в справочной системе Maple 7. Возможности пакетов linalg и LinearAlgebra удовлетворят самых требовательных специалистов в этой области математики.

Интеграция Maple 7 с MATLAB

Краткие сведения о MATLAB

Несмотря на обширные средства линейной алгебры (да и многие другие), имеющиеся у системы Maple 7, есть системы компьютерной математики, решающие некоторые классы задач более эффективно, и прежде всего быстрее. В области линейной алгебры к таким системам, безусловно, относится система MATLAB, созданная компанией Math Works, Inc. Ее название происходит именно от слов MATrix LABoratory — матричная лаборатория.

MATLAB содержит в своем ядре многие сотни матричных функций и является одной из лучших матричных систем для персональных компьютеров. Она реализует самые современные алгоритмы матричных операций, включая, кстати, и алгоритмы NAG. Однако главное достоинство MATLAB — наличие множества дополнительных пакетов как по классическим разделам математики, так и по самым новейшим, таким как нечеткая логика, нейронные сети, идентификация систем, обработка сигналов и др. Знаменитым стал пакет моделирования систем и устройств Simulink, включаемый в пакет поставки системы MATLAB. Последней версией системы является MATLAB 6.0. В то же время нельзя не отметить, что MATLAB — одна из самых громоздких математических систем. Инсталляция ее полной версии занимает около 1,5 Гбайт дискового пространства. Несмотря на это, интеграция различных математических систем с данной системой, похоже, становится своеобразной модой. Такая возможность предусмотрена и в системе Maple 7 с помощью пакета Matlab.

Загрузка пакета расширения Matlab

Для загрузки пакета Matlab используется команда: .

> with(Matlab);

[chol, closelink, defined, del, dimensions, eig, evalM,fft, getvar, inv, Iu,ode45, openlink, qr, setvar, size, square, transpose ]

Использование этой команды ведет к автоматическому запуску системы MATLAB (гарантируется работа с версиями MATLAB до 5.3.1 включительно) и установлению необходимой объектной связи между системами Maple 7 и MATLAB.

ПРИМЕЧАНИЕ

Как нетрудно заметить, данный пакет дает доступ всего к 18 функциям системы MATLAB (из многих сотен, имеющихся только в ядре последней системы). Таким образом, есть все основания полагать, что возможности MATLAB в интеграции с системой Maple 7 используются пока очень слабо и носят рудиментарный характер. Стоит ли ради этих функций иметь на компьютере огромную систему MATLAB, пользователи должны решать сами. Если ответ положительный, то, скорее всего, пользователь решает тот класс задач, для которых лучше подходит MATLAB, и надо задуматься уже над тем, нужен ли в этом случае Maple.

Типовые матричные операции пакета расширения Matlab

Большинство функций пакета Matlab (не путайте с системой MATLAB, имя которой надо записывать прописными буквами) реализуют самые обычные матричные операции, что и иллюстрируют приведенные ниже примеры.

Зададим матрицу М в формате Maple:

Ниже даны примеры транспонирования матрицы, ее инвертирования, вычисления детерминанта и собственных значений матрицы:

Можно проверить, является ли матрица квадратной:

Можно также проверить, является ли данная матрица матрицей системы MATLAB:

Здесь надо иметь в виду, что форматы матриц в системах Maple и MATLAB различны. Выполним LU-преобразование матрицы:

Таким образом, видно, что пакет Maple в данном случае реализует типовые матричные операции, но средствами системы MATLAB. Загрузка последней происходит автоматически при загрузке пакета Matlab. Если система MATLAB не установлена на вашем компьютере, то доступ к функциям пакета Matlab будет отсутствовать, a Maple 7 при попытке использования данных функций будет выдавать сообщения об ошибках.

Выделение сигнала на фоне шумов

Среди небольшого числа доступных функций системы MATLAB в пакете Matlab нельзя не выделить особо функции быстрого прямого и обратного преобразований Фурье. В системе MATLAB эти функции реализуют наиболее эффективные алгоритмы быстрого преобразования Фурье (БПФ), обеспечивающие решение крупноразмерных задач (например, обработки сигналов, представленных векторами и матрицами больших размеров) в десятки раз быстрее, чем при обычных методах выполнения преобразований Фурье.

Покажем возможность применения БПФ на ставшем классическим примере — выделении спектра полезного сигнала на фоне сильных помех. Зададим некоторый двухчастотный сигнал, имеющий 1500 точек отсчета:

> num := 1500:

Time := [seq(.03*t. t=l..num)]:

data := [seq((3.6*cos(Time[t]) + cos(6*Time[t])), t-l..num)]:

p1ots[pointp1ot](zlp((x,y)->[x,y],Time,data), style=1ine);

График сигнала представлен на рис. 15.1.

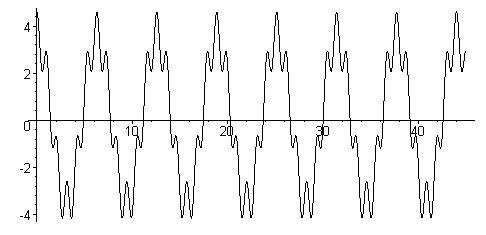
Рис. 15.1. График исходного сигнала

Теперь с помощью генератора случайных чисел наложим на этот сигнал сильный «шум» (слово «шум» взято в кавычки, поскольку речь идет 6 математическом моделировании шума, а не о реальном шуме физической природы):

> tol := 10000:

r := rand(0..to1):

noisyjlata :=[seq(r()/(tol)*data[t], t=l..num)]:

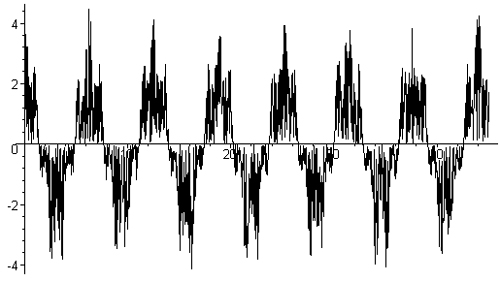
plots[pointp1ot](zip((x,y)->[x,y],T1me,noisy_data), sty1e=1ine);

Нетрудно заметить, что теперь форма сигнала настолько замаскирована шумом (рис. 15.2), что можно лишь с трудом -догадываться, что сигнал имеет периодическую составляющую малой амплитуды. Эта высокочастотная составляющая сигнала скрыта шумом.

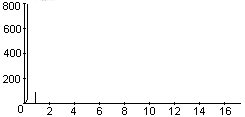
Подвергнем полученный сигнал (в виде временной зависимости) прямому преобразованию Фурье, реализованному функцией fft:

> ft := fft(noisy_data):

> VectorOptions(ft, datatype):

complex₈

Эта операция переводит задачу из временного представления сигнала в частотное, что позволяет использовать частотные методы анализа сигнала. Выделим, к примеру, действительную и мнимую части элементов вектора ft и проверим его размер:

Пакет анализа линейных функциональных систем LinearFunctionalSystems

Назначение пакета LinearFunctionalSystems

Пакет LinearFimctionalSystems содержит набор функций для решения задач, связанных с анализом линейных функциональных систем. Обычно такие системы описываются линейными дифференциальными уравнениями, имеющими то или иное решение. Пакет LinearFunctionalSystems позволяет провести тестирование подготовленной системы, оценить ряд ее параметров и получить решение одним из ряда методов.

Вызов всех функций пакета осуществляется командой:

> with(LinearFunctionalSystems):

[AreSameSolution, CanonicalSystem, ExtendSeries, Homogeneous System, IsSolution,

MatrixTriangularization, PolynomialSolution, Properties, RationalSolution,

SeriesSolution, UniversalDenominator]

Тестовые функции пакета LinearFunctionalSystems

Прежде чем рассматривать основные функции пакета, рассмотрим две тестовые функции. Они представлены следующими формами записи:

IsSolution(sol,sys, vars) IsSolution(sol, A, b, x, case)

IsSolution(sol, A, x, case) AreSameSolutior(sol, soil)

В них: sol — тестируемое решение, sys — система функциональных уравнений, х — независимая переменная решения, А и b — матрица и вектор с рациональными элементами, case — имя метода решения ('differential', 'difference' или 'qdifference').

Функции решения линейных функциональных систем

Группа основных функций пакета LinearFunctionalSystems имеет идентичный синтаксис и записывается в виде:

name(sys,vars,[method])

или

name(A[.b],x, case, [method]}

Здесь name — одно из следующих имен:

PolynomialSolution — решение в форме полинома;
RationalSolution — решение в форме рационального выражения;
SeriesSolution — решение в виде ряда;
UniversalDenominator — решение с универсальным знаменателем (и числителем, равным 1).

Система функциональных уравнений задается либо в виде полной системы sys со списком переменных vars, либо в матричном виде с заданием матриц коэффициентов, системы А и вектора свободных членов b (может отсутствовать) с указанием независимой переменной х и параметра case, имеющего значения 'differential', 'difference' или 'qdifference'. Параметр method, задающий метод EG-исключения, может иметь значения 'quasimodular' или 'ordinary'.

Вспомогательные функции

Несколько вспомогательных функций пакета LinearFunctionalSystems представлено ниже:

MatrixTriangularization(mat, m, n, x, It) — триангуляция матрицы mat размера mxn с указанием типа It ('lead' или 'trail');
CanonicalSystemCshift, sys. vars) или CanonicalSystemCshift, A[, b]. x, case) — возвращает систему в каноническом виде (параметр shift задается как ' difference' или ' q - difference', назначение других параметров С9ответствует указанным выше для других функций);
ExtendSeries(sol, deg) — расширяет ряд решения sol до расширенного ряда степени deg;
HomogeneousSystemChoitio, sys, vars) илиHomogeneousSystemChomo, A[, b], x, case) — преобразует исходную систему в гомогенную с именем homo.
PropertiesCsys, vars) или Properties(A[. b]. x, case) — возвращает основные свойства системы.

Примеры применения пакета LinearFunctionalSystems

Ниже представлен ряд примеров применения пакета LinearFunctionalSystems, иллюстрирующих его возможности:

Множество дополнительных примеров на анализ и решение линейных функциональных систем можно найти в справке по функциям данного пакета.

Что нового мы узнали?

В этом уроке мы научились:

Применять основные операции и определения линейной алгебры.
Использовать пакет решения задач линейной алгебры linalg.
Использовать пакет линейной алгебры LinearAlgebra с алгоритмами NAG.
Осуществлять интеграцию системы Maple 7 с матричной системой MATLAB.
Использовать некоторые функции системы MATLAB при работе в Maple 7.
Применять функции нового пакета LinearFunctionalSystems.

оглавление ДМ экономическая информатика визуальные среды - 4GL Теория и практика обработки информации

Знаете ли Вы, что оптимизационная модель - это математическая модель, имеющая форму задачи математического программирования и цель - нахождение некоторого оптимума.

НОВОСТИ ФОРУМА

Рыцари теории эфира