Задачи линейной оптимизации важны как в фундаментальных, так и в прикладных приложениях математики. В пакете simplex имеется небольшой, но достаточно представительный набор функций и определений для решения таких задач:
> with(simplex);
Warning, the protected names maximize and minimize have been redefined and unprotected
[basis, convexhull, cterm, deftne_zero, display, dual,feasible, maximize, minimize,pivot, pivoteqn, pivotvar, ratio, setup, standardize ]
Приведем краткое назначение этих функций:
Главными из этих функций являются maximize и minimize, оптимизирующие задачу симплекс-методом. Они записываются в следующих формах:
maximize(f, С)
minimize(f, С)
maximize(f , С, vartype)
nrinimize(f , С, vartype)
maximize(f , С,vartype, 'NewC', 'transform')
m'inimize(f , C, vartype, 'NewC', 'transform')
Здесь f — линейное выражение, С — множество или список условий, vartype — необязательно задаваемый тип переменных NONNEGATIVE или UNRESTRICTED, NewC и transform — имена переменных, которым присваиваются соответственно оптимальное описание и переменные преобразования. Ниже даны^примеры применения этих функций:
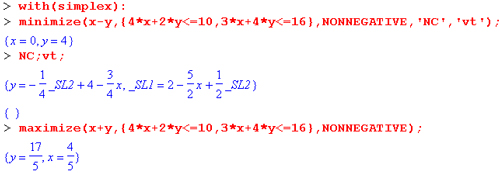
Функция basis(C) возвращает базис для системы линейных уравнений С. Например:
> basisC [ х - 2*z+w , z - 2*у - w ] );
[x,z]
Функция convexhull(ps) возвращает выпуклую оболочку множества точек ps:
> convexhum{[0,0],[l,l],[2,-l],[1,1/3],[1,1/2]}):
[[0,0],[2,-1],[1, 1]]
Для определения констант для системы линейных уравнений или неравенств служит функция cterm(C):
> cterm([2*х+у<=6.7*y-z-3-4]);
[6,7]
Функция define_zero(C) возвращает ближайшее ненулевое значение, зависящее от установки переменной Digits:

Функция display(C) имеет еще и форму display(C,[X, у, z]). Она задает вывод линейных уравнений и неравенств в матричной форме:

Функция dual(f, С, у) имеет следующие параметры: f — линейное выражение y, С множество неравенств и у — имя. Эта функция возвращает сопряженное с f выражение:
> dual( x-y,{2*x+3*y<=5.3*x+6*y<=15},z);
115zl +5z2, {1_<3z1+2z2,-l_<6z1+3z2}
Функция feasible может быть задана в трех формах:
feasible(C)
feasible(C,vartype)
feasible(C,vartype,'NewC','Transform')
Здесь параметр vartype может иметь значения NONNEGATIVE или UNRESTRICTED. Эта функция определяет систему как осуществимую или нет:
> feasible({2*x+3*y<-5, 3*x+6*y<"15}, NONNEGATIVE);
true
> feasib1e({2*x+3*y<-5, 3*х+б*у<—15}, NONNEGATIVE);
false
Если функция возвращает логическое значение true, то заданная система осуществима, а если false — неосуществима, то есть ни при каких значениях переменных не способна удовлетворить записанным неравенствам и равенствам. Функция pivot (С, х, eqn) конструирует новую систему с заданным главным элементом:
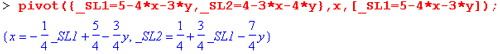
Функция pivoteqn(C, var) возвращает подсистему для заданного диагонального элемента С:
> pivoteqnC {_SL1 - 5-3*х-2*у. _SL2 - 4-2*х-2*у}. х );
[_SLl = 5-lx-2y]
Функция pivotvar(f, List) или pivotvar(f) возвращает список переменных, имеющих положительные коэффициенты в выражении для целевой функции:
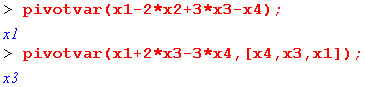
Функция ratio(C, x) возвращает список отношений, задающих наиболее жесткие ограничения:
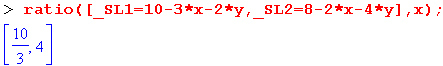
Функция setup может иметь три формы:
setup(C)
setup(C, NONNEGATIVE)
setup(C, NONNEGATIVE, 't')
Она обеспечивает конструирование множества уравнений с переменными в левой части:
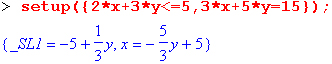
Последняя функция — standartlze(C) — конвертирует список уравнений (неравенств) в неравенства типа «меньше или равно»:
> standardize({2*x+3*y<-5.3*x+5*yl5});
{2х + Зу<5,Зх + 5у<15,-Зх-5у<-15}
Пакет геометрических расчетов geometry в системе Maple 7 получил как бы второе рождение число его функций по сравнению с версией этого пакета в системе Maple V R5 возросло в несколько раз. Теперь загрузка пакета возвращает весьма внушительный список из более чем 100 функций:
> with(geometry);
[Appolonius, AreCollinear, AreConcurrent, AreConcyclic, AreConjugate, AreHarmonic, AreOrthogonal, AreParallel, ArePerpendicular, AreSimilar, AreTangent, CirdeQfSimilitude,CrossProduct, CrossRatio, DefinedAs, Equation, EulerCircle, EulerLine, Exterior Angle, ExternalBisector, FindAngle, GergonnePoint, GlideRefledion, HorizontalCoord, HorizontalName, InteriorAngle, IsEquilateral,
IsOnCircle, IsOnLine, IsRightTriangle, MajorAxis, MakeSquare, MinorAxis,NagelPoint, OnSegment, ParallelLine, PedalTriangle, PerpenBisector, PerpendicularLine, Polar, Pole, RadicalAxis, RadicalCenter, RegularPolygon, RegularStarPolygon, SensedMagnitude, SimsonLine, SpiralRotation, StretchReflection, StretchRotation, TangentLine, VerticalCoord, VerticalName,
altitude, apothem, area, asymptotes, bisector, center, centroid, circle, circumcircle, conic, convexhull, coordinates, detail, diagonal, diameter, dilatation, directrix, distance, draw, dsegment, ellipse, excircle, expansion, foci, focus, form, homology, homothety, hyperbola, incircle, inradius, intersection, inversion, line, medial, median, method, midpoint, orthocenter, parabola, perimeter, point, powerpc, projection,
radius, randpoint, reciprocation, reflection, rotation, segment, sides, similitude, slope, square, stretch, tangentpc, translation, triangle, vertex, vertices}
Этот пакет содержит средства расчета основных параметров ряда геометрических объектов. Для каждого объекта возможно задание различных исходных величин, так что пакет охватывает практически все виды классических геометрических расчетов на плоскости. Несомненно, этот пакет заинтересует всех, кто работает в области геометрии и смежных областях.
Обратите внимание на то, что многие функции этого пакета вовсе не рисуют на экране соответствующие фигуры, а лишь выполняют типовые геометрические расчеты. Разумеется, в дальнейшем, используя результаты этих расчетов, можно построить соответствующую фигуру с помощью графических функций.
Пример применения расчетных функций пакета geometry
К сожалению, описание всех функций этого пакета потребует привести справочные данные практически по всей геометрии на плоскости, объем которых намного превышает объем данной книги. Учитывая идентичность идеологии при работе с функциями этого пакета, большинство из которых имеет вполне прозрачные имена (правда, англоязычные), работу с пакетом поясним на примере одной из функций — circle. Она позволяет математически задать окружность и определить все ее геометрические параметры. Функция может иметь несколько форм записи. Например, в форме:
circle(c,. [А. В. С], n, 'centername'=m)
она определяет построение окружности, проходящей через три точки А, В и С. Необязательный параметр n — список с именами координатных осей. Параметр ' centername' =m задает имя центра.
В форме circle(c. [А. В], n, 'centername'=m) задается окружность, проходящая через две точки А и В, а в форме circle(c, [A, rad], n, 'centername'=m) задается окружность, проходящая через одну точку А с заданным (и произвольным) радиусом rad и центром с. Наконец, функция circle в форме circle (с, eqn, n, 'centername'=m) позволяет задать окружность по заданным уравнению eqn и центру с. Проиллюстрируем применение функции circle на следующих примерах. Зададим характеристические переменные:
> EnvHorizontalName := m: _EnvVertlcalNane :=n;:
Определим окружность c1, проходящую через три заданные точки А, В и С с указанными после их имен координатами, и найдем координаты центра этой окружности:

Далее найдем радиус окружности:

и уравнение окружности, заданное в аналитическом виде:

Наконец, с помощью функции detail получим детальное описание окружности:

Заинтересованный в таких расчетах читатель может самостоятельно ознакомиться с другими функциями аналогичным образом, тем более, что в справочной системе этого пакета имеется множество примеров работы с его функциями.
Визуализация геометрических объектов с помощью пакета geometry
Одно из важных достоинств пакета geometry - возможность наглядной визуализации различных геометрических понятий, например графической иллюстрации доказательства теорем или геометрических преобразований на плоскости. Проиллюстрируем это на нескольких характерных примерах, заодно показывающих технику работы с рядом функций этого пакета.
Рисунок 16.1 показывает построение из множества окружностей фигуры - кардиоиды. Вопреки обычному построению этой фигуры, используется алгоритм случайного (но удовлетворяющего требованиям построения данной фигуры) выбора положений центров и радиусов окружностей.
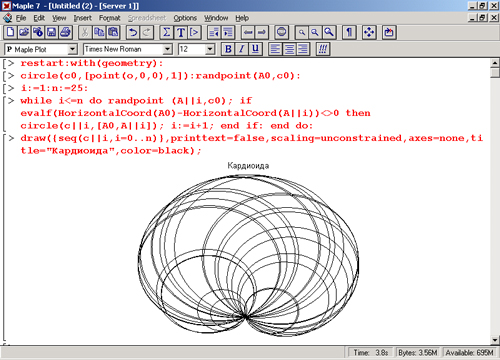
Рис. 16.1. Построение кардиоиды из окружностей
Рисунок 16.2 дает графическую иллюстрацию к одной из теорем Фейербаха. Здесь эффектно используются средства выделения геометрических фигур цветом, что, увы, нельзя оценить по книжной черно-белой иллюстрации.
На следующем рисунке (рис. 16.3) показано построение фигуры, образованной вращением множества квадратов относительно одной из вершин. Это хороший пример применения функций point, square,.rotation и draw из пакета geometry.
Рисунок 16.4 показывает гомологические преобразования квадрата. Заинтересовавшийся читатель может легко разобраться с деталями простого алгоритма этой программы.
ПРИМЕЧАНИЕ
Обратите особое внимание на последний параметр в функции draw. Он задает построение титульной надписи с заданными шрифтом и размером символов. Сравните титульные надписи на рис. 16.4 и 16.3, где титульная надпись сделана шрифтом, выбранным по умолчанию. Приятно, что в обоих случаях нет преград для использования символов кириллицы и создания надписей на русском языке.
Наконец, на рис. 16.5 показан пример построения трех окружностей, имеющих две общие точки. Обратите внимание на вывод надписей «о», «ol» и «о2», указывающих положение центров окружностей на рисунке.
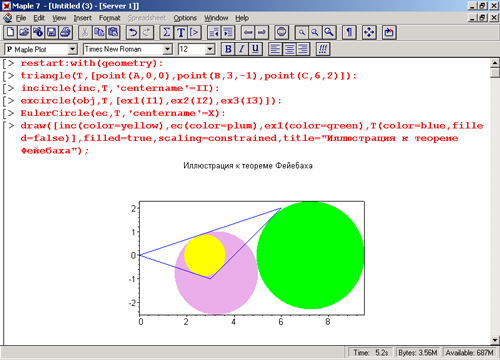
Рис. 16.2. Графическая иллюстрация к теореме Фейербаха

Рис. 16.3. Фигура, полученная вращением квадрата

Рис. 16.4. Гомологические преобразования квадрата
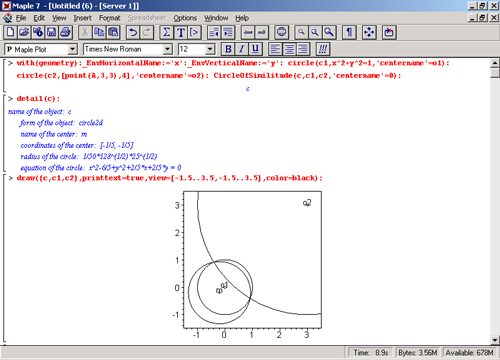
Рис. 16.5. Три окружности, имеющие две общие точки
Множество примеров применения всех функций пакета geometry дано в справочной системе Maple 7. Рекомендуется просмотреть те из них, которые нужны вам.
Помимо существенного расширения пакета geometry в систему Maple 7 введен новый геометрический пакет geonfld. Он предназначен для решения задач в области трехмерной геометрии. При загрузке пакета появляется доступ к большому (свыше 140) числу новых функций:
> with(geom3d);
[Archimedean, AreCollinear, AreConcurrent, AreConjugate, AreCoplanar, AreDistinct, AreParallel, ArePerpendicular, AreSameObjects, AreSamePlane, AreSkewLines, DefinedAs, DirectionRatios, Equation,'FindAngle, FixedPoint, GlideReflect, GlideReflection, GreatDodeeahedron, Greatlcosahedron, GreatRhombicuboctahedron, GreatRhombiicosidodecahedron,
GreatStellatedDodecahedron,HarmonicConjugate,
HexakisIcosahedron,Hexakis Octahedron, JnRadius,
Is Archimedean, IsEquilateral, IsFacetted,
IsOnObject, IsQuasi,hRegular,
IsRightTriangletIsStellated,IsTangent,
MidRadius, NormalVector, OnSegment, ParallelVector, PentagonalHexacontahedron, PentagonallcositetrahedronjPentakisDodecahedron, QuasiRegularPolyhedron,
RadicalCenter, RadicalLine,RadicalPlane, RegularPolyhedron, RhombicDodecahedron, RhombicTriacontahedron, Rotatory Reflect, Rotatory Reflection, ScrewDisplace, ScrewDisplacement, SmallRhombicubactahedron, SmallRhombiicosidodecahedron, SmallStellatedDodecahedron, SnubCube, SnubDodecahedron, StereographicProjection, StretchRotate, TangentPlane,
TetrakisHexahedron, TrapezoidalHexecontahedron, Trapezoidallcositetrahedron, Triakislcosahedron, TriakisOctahedron, TriakisTetrahedron, TruncatedCuboctahedron, TruncatedDodecahedron,TruncatedHexahedron, Truncatedlcosahedron, Truncatedlcosidodecahedron, TruncatedOctahedron, TruncatedTetrahedron, altitude, area, center, centroid, circle, coordinates, cube,
cuboctahedron, detail, dilate, distance, dodecahedron, draw, dsegment, duality,faces, facet, form, gtetrahedron, hexahedron, homology, homothety, icosahedron, icosidodecahedron, identity, incident, intersection, inverse, inversion, line, midpoint, octahedron, parallel, parallelpiped, plane, point, polar, pole, powerps, projection, radius, rqndpoint, reflect^ reflection, rotate, rotation, schlafli, segment, sides, sphere, stellate, tetrahedron, tname, transform, translate, translation, transprod, triangle, unit, valuesubs, vertices, volume, xcoord, xname, ycoord, yname, zcoord, zname ]
Функции этого пакета обеспечивают задание и определение характеристик и параметров многих геометрических объектов: точек в пространстве, сегментов, отрезков линий и дуг, линий, плоскостей, треугольников, сфер, регулярных и квазирегулярных полиэдров, полиэдров общего типа и др. Для описания функций этого пакета пришлось бы воспроизвести обширное справочное руководство по стереометрии. В то же время назначение функций ясно из их названия, а характер применения тот же, что для функций описанного выше пакета geometry.
Пример применения пакета geom3d
Учитывая сказанное, ограничимся единственным примером применения этого пакета (рис. 16.6).

Рис. 16.6. Иллюстрация применения пакета geom3d
Напоминаем, что цель пакета не в построении рисунков геометрических фигур, а в аналитическом представлении объектов в пространстве. Поэтому в обширной базе данных справочной системы по этому пакету вы встретите очень много рисунков.
Пакет для работы с алгебраическими кривыми algcurves
Пакет для работы с алгебраическими кривыми прекрасно дополняет возможности геометрических пакетов. При обращении к нему он дает доступ к полутора десяткам функций:
> restart;with(algcurves);
[Weierstrassform, differentials, genus, homogeneous, homology, integral_basis, isjiyperelliptic, j_invariant, monodromy,parametrization ,periodmatrix,plot_knot,puiseux, singularities ]
Ввиду важности функций пакета и их сравнительно небольшого числа приведем полную форму записи функций и их назначение:
Примеры применения пакета algcurves
Приведем примеры применения функций пакета algcurves:


Построение алгебраических кривых класса knot
Функция plot_knot позволяет строить одну или несколько алгебраических кривых — узлов. Пример построения целого семейства узлов показан на рис. 16.7.
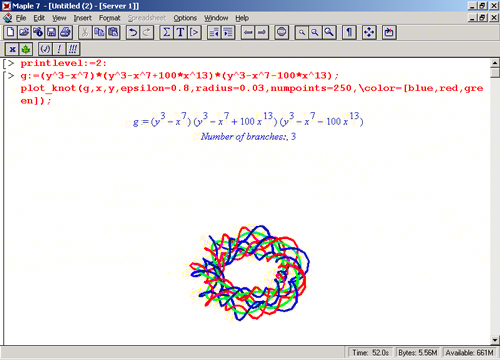
Рис. 16.7. Семейство узлов
Для лучшего обзора таких кривых рекомендуется воспользоваться возможностью вращения трехмерных фигур мышью для уточнения угла, под которым рассматривается фигура — в нашем случае семейство алгебраических кривых. Построение на рис. 16.7 выполняется довольно медленно — даже на компьютере с процессором Pentium III 600 МГц оно занимает около минуты.
Новая функция Maple 7 plot_real_curve
В пакет расширения algcurves добавлена новая функция импликативной графики plot_real_curve. Она строит алгебраическую кривую для действительной части полиномиального выражения и записывается в виде:
plot_real_curve (p, х, у, opt)
Функция имеет следующие параметры:
• showArrows = true или false — задает показ стрелок касательных или перпендикулярных к точкам вдоль кривой (по умолчанию false);
• arrowIntervalStep = posint — задает число точек, пропускаемых до показа очередной пары стрелок (по умолчанию 10);
• arrowScaleFactor = positive — задает масштаб для длины стрелок (по умолчанию 1);
• colorOfTangentVector = с — задает цвет касательных стрелок, по умолчанию заданный как зеленный, COLORCRGB,0,1,0);
• colorOfNormalVector = с — задает цвет перпендикулярных стрелок, по умолчанию заданный как красный, COLOR (RGB ,1,0,0);
• colorOf Curve = с — задает цвет кривой, по умолчанию заданный как синий, COLOR(RGB, 0, 0, 1);
• eventTolerance = positive — задает погрешность при представлении сингулярных точек (по умолчанию 0,01);
• NewtonTolerance = positive — задает погрешность при выполнении ньютоновских итераций в ходе построений.
Функция plot_real_curve вычисляет и строит алгебраическую кривую по точкам и может (при использовании параметра opt) строить стрелки-векторы по касательным и перпендикулярным направлениям к каждой точке или к части точек. Возможно задание разных цветов для кривой и стрелок. Применение функции plot_real_curve показывает рис. 16.8.
При задании построения стрелок касательные стрелки строятся по внешней части кривой и указывают направление ее построения. Перпендикулярные стрелки строятся по внутренней части кривой. Нетрудно заметить, что острие стрелки указывается только для длинных стрелок. Короткие стрелки острия не имеют и отображаются как отрезки прямых линий. Построение стрелок оказывается не вполне точным, если разнятся масштабы графика по горизонтали и вертикали, что можно подметить при внимательном рассмотрении графика на рис. 16.8, сверху.

Рис. 16.8. Примеры применения функции plot_real_curve
Пакет функций теории графов networks
Графы широко используются при решении многих прикладных и фундаментальных задач. Пользователей, занятых решением таких задач, наверняка порадует пакет networks, содержащий весьма представительный набор функций:
> with(networks);
Warning, the names diameter, draw and vertices have been redefined[acycpoly, addedge, addvertex, adjacency, allpairs, ancestor, arrivals,bicomponents, charpoly, chrompoly, complement, complete, components, connect, connectivity, contract, countcuts, counttrees, cube,cycle, cyclebase, daughter, degreeseq, delete, departures, diameter,dinic, djspantree, dodecahedron, draw, duplicate, edges, ends,eweight,flow,flowpoly,fundcyc, getlabel, girth, graph, graphical,gsimp,gunion,
head, icosahedron, incidence, incident, indegree, induce, isplanar,maxdegree, mincut, mindegree, neighbors, new, octahedron, outdegree,path,petersen, random, rank, rankpoly, shortpathtree, show,shrink, span, spanpoly, spantree, tail, tetrahedron, tuttepoly, vdegree,vertices, void, vweight]
Объективности ради надо отметить, что в Maple 7 из этого пакета удалено несколько второстепенных функций, которые были в версии Maple V R5. Теория графов используется достаточно широко даже при решении прикладных задач — например, для вычисления оптимальных маршрутов движения железнодорожных составов, наиболее целесообразной раскройки тканей и листов из различных материалов и т. д.
Примеры применения пакета networks
Рассмотрим некоторые избранные функции этого пакета, которые наиболее часто используются при работе с графами. Детали синтаксиса функций можно найти в справочной базе данных Maple 7.
Функции создания графов:
Функции с типовыми возможностями графов:
Каждая из этих команд имеет одну или несколько синтаксических форм записи. Их можно уточнить с помощью справочной системы. С ее помощью можно ознакомиться и с назначением других функций этого обширного пакета. Проиллюстрируем его применение на нескольких типичных примерах.
На рис. 16.9 показан пример создания Графа, имеющего четыре вершины, и графа Петерсона с выводом их графиков графической функцией draw.
На рис. 16.10 показан другой пример работы с графами — построение графа функцией complete и затем его преобразование путем удаления части вершин. Исходный и преобразованный графы строятся функцией draw.
В третьем примере (рис. 16.11) граф формируется по частям — вначале задается пустой граф функцией new, а затем с помощью функций addvertex и addedge в него включаются вершины и ребра. Далее функция connect соединяет вершину а с вершиной с, делая граф замкнутым. Функция draw строит сформированный таким образом граф, а функции head и tail используются для выявления «голов» и «хвостов» графа.
В четвертом примере, представленном на рис.,16.12, показано создание графа G2 (его изображение было приведено на рис. 16.10) с вычислением для этого графа максимального потока от вершины 1. Обратите внимание, что в параметрах функции flow, использованной для этого, заданы две переменные: eset — принимает значение множества с ребрами, по которым проходит максимальный поток, и соmр — принимает значение множества, в котором содержатся вершины, по которым проходит максимальный поток. Значения этих переменных выведены в области вывода. В заключительной части этого примера показано применение функции shortpathtree, ищущей наиболее короткий путь от вершины 1 до других вершин.
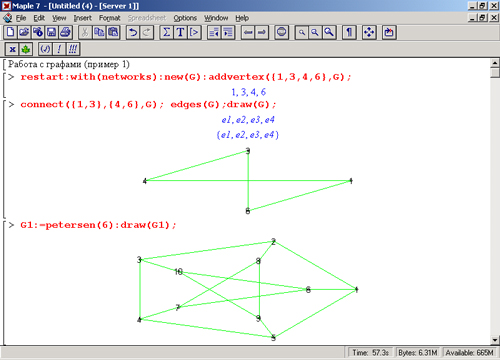
Рис. 16.9. Построение графов
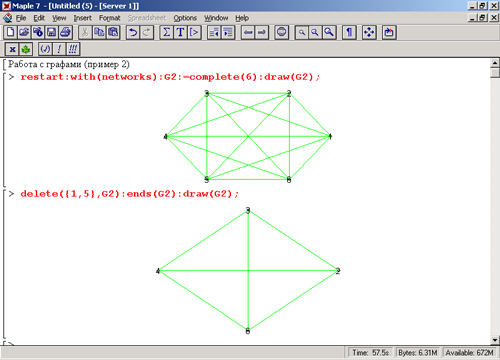
Рис. 16.10. Преобразование графа удалением части вершин
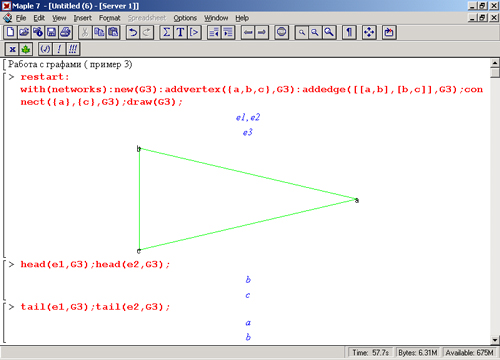
Рис. 16.11. Формирование графа и определение его «голов» и «хвостов»
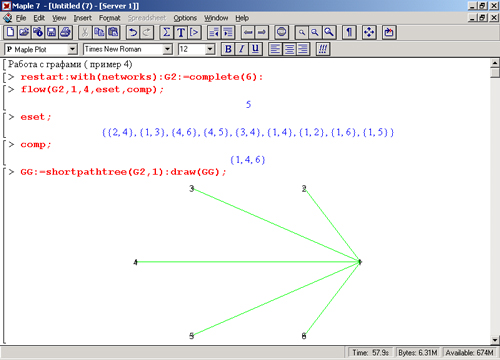
Рис. 16.12. Пример вычисления максимального потока и наиболее коротких путей для заданного графа
Еще один пример, приведенный ниже, иллюстрирует работу функции show, выдающей таблицу с полной информацией о графе, созданном функцией complete:

Разумеется, приведенные примеры далеко не исчерпывают всех задач, которые можно решать с применением графов. Но они наглядно демонстрируют, что для большинства пользователей пакет networks превращает графы из окутанного ореолом таинственности модного средства в простой рабочий инструмент.
Пакет статистических расчетов stats
Мир математических систем сейчас насыщен статистическими системами, например такими, как Statistica или StatGraphics. Они прекрасно приспособлены для решения задач статистической обработки обширных массивов данных. Тем не менее проведение статистических расчетов в Maple 7 возможно и в ряде случаев весьма целесообразно — например, когда они являются частью исследовательского проекта.
Пакет stats для таких расчетов представлен всего двумя многоцелевыми статистическими функциями:
stats[subpackage, functionj(args)
subpackage[function](args)
Однако благодаря специальной форме задания параметров (в частности, в виде подпакетов — subpackages) возможно вычисление самых разнообразных статистических функций. Имеются следующие подпакеты:
Генерация случайных чисел с заданным распределением
Основой этого подпакета является функция random:
random[distribution] (quantity,unifarm,method)
или
stats[random, distribution] (quantity,unifofm,method)
где
Возможно задание дискретных и непрерьвных распределений, например binomiald --дискретное биномиальное распределение, discreteumform — дискретное 'равномерное распределение, empirical — дискретное эмпирическое распределение, poisson — дискретное распределение Пуассона, beta — бета-распределение, cauchi — .распределение Коши, exponential — экспоненциальное и др. (есть функции практически для всех известных распределений).
Следующие примеры демонстрируют технику получения случайных чисел с заданным законом распределения;
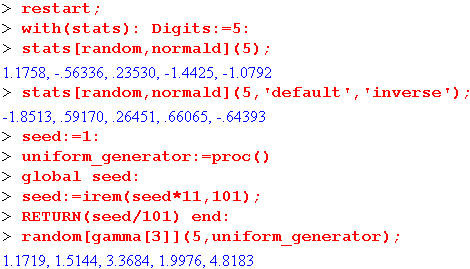
Графика статистического пакета stats
Статистический пакет stats имеет свою небольшую библиотечку для построения графиков. Она вызывается в следующем виде:
stats[statplots, function](args)
или
statplots[function](args)
Вид графика задается описанием function: boxplot, histogram, notehedbox, quantile, quantile2, scatterld, scatter2d и symmetry. Данные функции обеспечивают построение типовых графиков, иллюстрирующих статистические расчеты. В качестве примера на рис. 16.13 показано задание множества случайных точек и его отображение на плоскости в ограниченном прямоугольником пространстве.
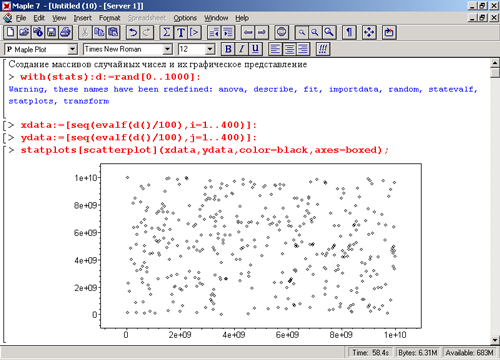
Рис. 16.13. Создание случайных точек и построение их на плоскости
По равномерности распределения точек можно судить о качестве программного генератора случайных чисел, встроенного в Maple 7.
Довольно часто для визуализации вычислений используется построение гистограмм. Для их создания пакет stats имеет функцию histogram:
stats[statplotsб histogram](data) :
statplots[h1stogram](data)
stats[statplots, histogram[scale](data)
statp1ots[histogram[scale](data)
Здесь data — список данных, scale — число или описатель. Детали применения этой простой функции поясняет рис. 16.14. На нем дан два примера — построение столбцов заданной ширины и высоты и построение гистограммы 100 случайных чисел с нормальным распределением.
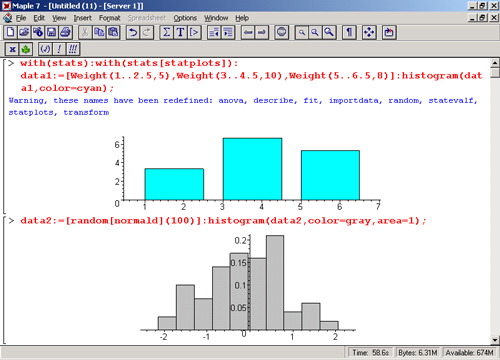
Рис. 16.14. Построение гистограмм
Обратите внимание на то, что для второго примера гистограмма будет несколько меняться от пуска к пуску, так как данные для ее построения генерируются случайным образом.
Под регрессионным анализом (или просто регрессией) обычно подразумевают нахождение некоторой формальной аналитической зависимости, которая приближенно (по критерию минимума среднеквадратической ошибки) аппроксимирует исходную зависимость. Последняя чаще всего бывает представлена некоторым набором точек (например, полученных в результате эксперимента).
Для проведения регрессионного анализа служит функция fit, которая вызывается следующим образом:
stats[fit,leastsquare[vars,eqn.parms]](data)
или
fit[leastsquare[vars,eqn.parms]](data)
где data — список данных, vars — список переменных для представления данных, eqn — уравнение, задающее аппроксимирующую зависимость (по умолчанию линейную), parms — множество параметров, которые будут заменены вычисленными значениями.
На приведенных ниже примерах показано проведение регрессии с помощью функции fit для зависимостей вида у(х):
> with(stats):Digits:=5;
Digits := 5
> fit[leastsquare[[x,y]]]([[l,2,3,4].[3,3.5,3.9,4.6]]);
у = 2.4500 + .52000 х
>fit[leastsquare[[x,y], y=a*x"2+b*x+c]]([[l.2,3.4],[1.8,4.5,10,16.5]]);
2
у = .95000 х + .21000 х + .55000
В первом примере функция регрессии не задана, поэтому реализуется простейшая линейная регрессия, и функция fit возвращает полученное уравнение регрессии для исходных данных, представленных списками координат узловых точек. Это уравнение аппроксимирует данные с наименьшей среднеквадратичной погрешностью. Во втором примере задано приближение исходных данных степенным многочленом второго порядка. Вообще говоря, функция fit обеспечивает приближение любой функцией полиномом.
Рисунок 16.15 показывает регрессию для одних и тех же данных Полиномами первой, второй и третьей степени с построением их графиков и точек исходных данных. Нетрудно заметить, что лишь для полинома третьей степени точки исходных данных точно укладываются на кривую полинома, поскольку в этом случае (4 точки) регрессия превращается в полиномиальную аппроксимацию. В других случаях точного попадания точек на линии регрессии нет, но обеспечивается минимум среднеквадратической погрешности для всех точек — следствие реализации метода наименьших квадратов.
Функция fit может обеспечивать регрессию и для функций нескольких переменных. При этом надо просто увеличить размерность массивов исходных данных. В качестве примера ниже приведен пример регрессии для функции двух переменных:
>f:=fit[1eastsquare[[x,y,z],z=-a+b*x+c*y,{a,b,c}]]\
([[l,2,3.5,5],[2.4,6,8.8],[3,5,7,10,Weight(15,2)]]):
f:=z=l + 13/3x-7/6y
> fa:=unapply(rhs(f),x,y);
fa:=(x,y)->l + 13/3x-7/6y
z > fa(1.,2.);
2.999999999
>fa(2,3):
37/6

Рис. 16.15. Примеры регрессии полиномом и первой, второй и третьей степени
В данном случае уравнение регрессии задано в виде z = a + bx + cy. Обратите внимание на важный момент в конце этого примера — применение полученной функции регрессии для вычислений или построения ее графика. Прямое применение функции f в данном случае невозможно, так как она представлена в не вычисляемом формате. Для получения вычисляемого выражения она преобразуется в функцию двух переменных fa(x,y) путем отделения правой части выражения для функции f. После этого возможно вычисление значений функции fa(x,y) для любых заданных значений х и у:
К сожалению, функция fit неприменима для нелинейной регресии. При попытке ее проведения возвращается структура процедуры, но не результат регресии — см. пример ниже:

Для проведения нелинейной регрессии произвольного вида нужно обратиться к средствам нового пакета CurveFitting, включенного в состав Maple 7. Этот пакет был описан в главе 14.
Пакет student — это, несомненно, один из пакетов, наиболее привлекательных для студентов и аспирантов. В нем собраны наиболее распространенные и нужные функции, которые студенты университетов и иных вузов обычно используют на практических занятиях, при подготовке курсовых и дипломных проектов. Набор этих функций, разумеется, не ограничивается «скромными» потребностями студентов — просто это наиболее распространенные функции, в основном относящиеся к математическому анализу. Наряду со студентами эти функции широко используют профессионалы-математики и ученые, применяющие математические методы в своей работе.
В этом пакете имеется почти полсотни функций:
Функции интегрирования пакета student
В пакетах Maple 7 можно найти множество специальных функций для вычисления интегралов различного типа. Например, в пакете student имеются следующие функции:
Ниже дан пример применения функции Tripleint пакета student:

Объективности ради надо отметить, что вычисление тройного интеграла с помощью функции Tripleint занимает много времени (около 20 с на компьютере с процессором Pentium II 350 МГц). 'Однако тот же результат (см. последний пример) получается за доли секунды при использовании тройного интегрирования с помощью функции int.
Иллюстративная графика пакета student
Пакет student имеет три графические функции для иллюстрации интегрирования методом прямоугольников:
Здесь f (x) — функция переменной х, х — переменная интегрирования, а — левая граница области интегрирования, b — правая граница области интегрирования, n — число показанных прямоугольников, color — цвет прямоугольников, о — параметры (см. ?plot,options).
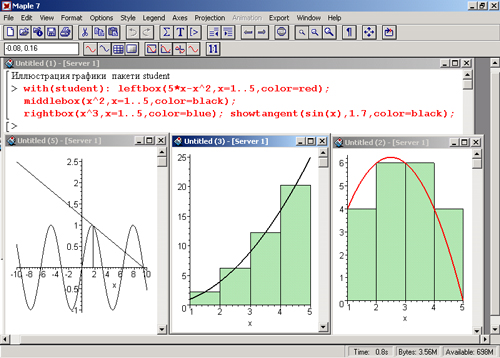
Рис. 16.16. Примеры иллюстративной графики пакета student
В этих функциях прямоугольники строятся соответственно слева, справа и по середине относительно узловых точек функции f(x), график которой также строится. Кроме того, имеется функция для построения касательной к заданной точке х = а для линии, представляющей f(x):
showtangent (f(x), x = а)
Рисунок 16.16 показывает все эти возможности пакета student. Три вида графиков здесь построены в отдельных окнах.
Графические средства пакета student ограничены. Но они предоставляют как раз те возможности, которые отсутствуют в основных средствах построения графиков.
Пакет для работы с тензорами tensor
Этот пакет впервые появился в реализации Maple V R5. Он дает средства для работы с тензорами и вычислениями, используемыми в общей теории относительности. В нем использован специальный тип данных tensor_type в виде таблиц с двумя полями: компонентов и характеристик индексов. Поле компонентов — массив с размерностью, эквивалентной рангу объекта. Поле характеристик индексов задается списком чисел 1 и -1. При этом 1 на i-й позиции Означает, что соответствующий индекс контрвариантный, а -1 — что он ковариантный.
Процедура tensor_type возвращает логическое значение true, если ее первый аргумент удовлетворяет свойствам тензора, и false, если он этому свойству не удовлетворяет.
Каждому тензору соответствуют еще две таблицы. Таблица коэффициентов вращения задает коэффициенты вращения Ньюмена—Пенроуза, которые вычисляются функцией tensor[npspin] и индексируются именами греческих букв alpha, beta, gamma, epsilon и т. д. Другая таблица (компонент кривизны) содержит компоненты кривизны Ньюмена—Пенроуза. Они представлены тремя полями: полем Phi в виде массива размерности (0..2.0..2) с компонентами Риччи, поле Psi с массивом размерности (0. .4) с компонентами Вейля и полем R со скаляром Риччи.
Объявление:
> with(tensor);
[Christoffell, Christoffel2, Einstein, Jacobian, Killing_eqns, LevijCivita, Lie_diff, Ricci, Ricciscalar, Riemann, RiemannF, Weyl, act, antisymmetrize, change_basis, commutator,
compare, conj, connexF, contract, convertNP, cov_diff,
create,dlmetric, d2metric, directional_diff, displayGR, display_allGR, dual, entermetric, exteriorjiiff, exterior_prod, frame,geodesic_eqns, get_char, get_compts,get_rank, init, invars, invert, lin_com, lower, npcurve, npspin, partial_diff, permute_indices, petrov, prod, raise, symmetrize, tensorsGR, transform}
дает доступ к следующим функциям пакета:
Примеры применения этого пакета можно найти в справочной базе данных системы. Пакет представляет интерес для физиков-теоретиков, работающих в области общей теории относительности и ее приложений/Для них (но не для большинства пользователей) приведенные данные полезны и понятны.
Этот небольшой пакет служит для создания доменов — таблиц операций для вычислений. При его загрузке появляется сообщение о переопределениях объектов и список из всего лишь шести функций:
>restart;with(Domains):
Domains version 1.0
Initially defined domains are Z and Q the integers and rationale Abbreviations, e.g. DUP for DenseUnivariatePolynomial, also made Warning, the protected names Array, Matrix and Vector have been redefined and unprotected [Array, Matrix, Matrixlnverse, Vector, init, show]
Пакет допускает применение следующих конструкций:
Domains[domain] Doma1ns[evaldomains]
Domains[example] Domains[coding]
Приведенный ниже пример поясняет создание и использование доменов Q (для рациональных
данных) и Z (для целочисленных данных):
> Q['+'](l/2,2/5,3/8);
51/40
> Z[Gcd](660,130);
10
Следующая операция показывает, что домен Z является таблицей:
> type(Z,table);
true
А функция show позволяет вывести полный перечень всех операций, доступных для домена Z:
> show(Z,operations);
Signatures for constructor Z'
note: operations prefixed by -- are not available
*: (Integers,Z) ->Z
* :(Z,Z*) ->Z
+ :(Z,Z*) ->Z
-: (Z,Z) -> Z'
- :Z ->Z
0:Z
1:Z
< :(Z,Z) -> Boolean
<= : (Z.Z) -> Boolean
<> : (Z.Z) -> Boolean
=:(Z.Z) -> Boolean
>: (Z.Z) -> Boolean
>-: (Z.Z) -> Boolean
Abs : Z ->Z
Characteristic : Integers
Coerce : Integers-> Z
Div : (Z.Z) -> Union(Z,.FAIL)
EuclideanNorm : Z -> Integers
Factor : Z -> [Z,.[[Z,Integers]*]]
Gcd : Z* -> Z
Gcdex : (Z,Z,Name) ->Z
Gcdex : (Z,.Z,Name,Name) -> Z
Input : Expression -> Union(Z,.FAIL)
Inv : Z -> Union(Z,FAIL)
Lcm : Z* -> Z
Max : (Z,Z*) -> Z
Min : (Z,.Z*)-> Z
Modp : (Z,.Z) ->Z
Mods : (Z.Z)--> Z
ModularHoraomorphlsm : () -> (Z -> Z.Z)'
Normal : Z -> Z
Output : Z -> Expression
Powmod : (Z,Integers,Z) -> Z
Prime : Z -> Boolean
Quo : (Z,.Z,Name) ->Z
Quo : (Z,.Z) -> Z
Random : О ->Z
RelativelyPrime : (Z,.Z) -> Boolean'
Rem : (Z,.Z,.Name)-> Z
Rera : (Z,Z) -> Z
Sign : Z -> UNIONU,.-l,0)
SmallerEuclideanNorm : (Z,.Z) -> Boolean
Sqrfree : Z ->[Z,.[[Z,.Integers]*]]
Type : Expression -> 'Boolean'
Unit : Z -> Z
UnitNormal : Z -> [Z,.Z,.Z]
Zero : Z -> Boolean
^ : (Z,Integers) -> Z.
Домены позволяют передавать в качестве параметра процедур набор функций в виде единого целою, что и объясняет название этих объектов. Предполагается, что это может привести к заметному сокращению кодов программ вычислений в будущих реализациях системы Maple. Пока же возможности доменов скорее выглядят как очередная экзотика, чем как реальное средство для оптимизации вычислений. Потребуется время, чтобы показать, что это не так.
Обзор пакетов узкого назначения
Мы уже не раз обращали внимание читателя на выборочный характер описания системы Maple 7 в данной книге. Хотя она и является одной из самых полных книг по данной системе, книга не претендует на роль детального справочника по Maple 7: Более того, такого справочника в виде книги нет и, вероятно, учитывая быстрые темпы модернизации программы, так и не будет. Для подобного описания Maple пришлось бы подготовить многотомное издание, охватывающее практически все области математики.
Учитывая это, мы вынуждены отказаться от попытки описать ряд пакетов специального назначения. Такими пакетами интересуются серьезные специалисты в области математики и им (не без труда, разумеется) под силу разобраться с назначением функций таких пакетов и примерами их применения, приведенными в справочной системе Maple 7. В связи с выше сказаннным, мы ограничимся перечислением оставшихся неизученными пакетов.
Пакет функций теории чисел numtheory
В этом обширном пакете собрано 46 функций, относящихся к теории чисел:
> with(numtheory);
Warning, the protected rame order has been redefined and unprotected
[GIgcd, bigomega, cfrac, cfracpol, cyclotomic, divisors ;factorEQ,factorset,fermat, imagunit, index, integral_basis, invcfrac, invphi, issqrfree,jacobi, kronecker, Я,legendre, mcombine, mersenne, minkowski, mipolys, mlog, mobius, mroot, msqrt, nearestp, nthconver, nthdenom, nthnumer, nthpow, order,pdexpand, ф,n,pprimroot,primroot, quadres, rootsunity, safeprime, o,sq2factor, sum2sqr, т,thue ]
В новой реализации Maple 7 число функций было уменьшено. Большинство функций этого пакета достаточно просты и заинтересовавшийся читатель вполне в состоянии провести их тестирование самостоятельно.
Пакет для работы с р-адическими числами padic
Этот весьма специфический пакет содержит следующие функции для работы с р-адическими числами:
> with(padic);
[arccoshp, arccosp,arccothp, arccotp, arccschp, arccscp, arcsechp, arcsecp, arcsinhp, arcsinp, arctanhp, arctanp, coshp, cosp, cothp, cotp, cschp, cscp, evalp, expansion, expp, Icoeffp, logp, orderp, ordp, ratvaluep, rootp, sechp, seep, sinhp,sinp, sqrtp, tanhp,tanp, valuep]
В Maple 7 число функций этого пакета увеличено почти в четыре раза. Однако ввиду специфичности данных функций их изучение мы оставляем за читателем для самостоятельной работы.
Пакет для работы с гауссовыми целыми числами Gausslnt
Гауссово целое число — это число вида а + I*b, где а и b — любые целые рациональные числа. Таким образом, они образуют решетку всех точек с целыми координатами на плоскости комплексных чисел. Пакет Gausslnt содержит достаточно представительный набор функций для работы с этими числами:
> with(GaussInt):
Warning, the name GIgcd has been redefined
[GIbasis, Glchrem, GIdivisor, GIfacpoly, GIfacset, GIfactor, GIfactors, GIgcd, GIgcdex, Glhermite, Glissqr, Gllcm, GImcmbine, GInearest, GInodiv, GInorm, Glnormal, Glorder, GIphi, GIprime, Glquadres, Glquo, GIrem, GIroots, GIsieve, GIsmith ,GIsqrfree, GIsqrt, Glunitnormal ]
Нетрудно заметить, что в этот набор входят уже известные числовые функции, к именам которых добавлены буквы 61. Например, функция GIfactor(c) раскладывает гауссово число (в том числе комплексное) на простые множители, GIgcd(cl, с2) находит наибольший общий делитель гауссовых чисел cl и с2 и т. д. Функции этого пакета достаточно просты, так что ограничимся приведенными примерами. Гауссовы целые числа в большинстве научно-технических расчетов встречаются крайне редко. Так что этот пакет рассчитан на специалистов-математиков, работающих в области теории чисел.
Пакет алгебры линейных операторов Ore_algebra
Пакет Ore_algebra содержит набор функций алгебры линейных операторов, состав которого виден после обращения к пакету:
> with(0re_algebra);
[OrejoJDESol, Ore_to_RESol, Orejojdiff, Ore_to_shift, annihilators, applyopr, diff_algebra, poly, algebra, qshiji_algebra, rand_skew_poly, shift_algebra, skew_algebra, skewjslim, skewjgcdex, skewjydiv, skewjxrwer, skew_prem, skew_product]
Этот пакет поддерживает решение задач в области алгебры линейных операторов.
Инструментальный пакет для линейных рекуррентных уравнений LREtools
Этот пакет полезен математикам, часто использующим рекуррентные отношения и формулы. Он дополняет функцию rsolve основной библиотеки и содержит следующие функции: :
> with(LREtools):
[REcontent, REcreate, REplot, REprimpart, REreduceorder, REtoDE,REtodelta, REtoproc, autodispersion, constcoeffsol,
5,dispersion, divconq, firstlin, hypergeomsols, polysols,ratpolysols, riccati, shift]
С назначением функций этого пакета можно познакомиться по справочной системе Maple 7.
Пакет функций дифференциальных форм difforms
В пакете дифференциальных форм содержится следующий ряд функций:
> with(difforms);
[&^, d, defform,formpart,parity, scalarpart, simpform, wdegree]
Демонстрационные материалы по применению этого пакета входят в поставку Maple 7.
Пакет для работы с рациональными производящими функциями genfunc
В пакете genfunc, предназначенном для работы с производящими функциями, содержатся следующие средства:
> with(genfunc);
[rgf_charseq, rgf_encode, rgf_expqnd, rgfjindrecur, rgfjiybrid, rgfjiorm, rgf_pfrac, rgf_relate, rgf_sequence, rgf_simp, rgfjerm,termscale]
Эти функции представляют специальный интерес для пользователей, работающих в области теории чисел и рациональных функций.
Пакет операций для работы с конечными группами group
Этот пакет содержит довольно представительный набор функций для работы с конечными группами:
> with(group);
[DerivedS, LCS, NormalClosure, RandElement, SnConjugates, Sylow,areconjugate, center,
centralizer, core, cosels, cosrep, derived, elements,groiipmember,grouporder, inter, invperm, isabelian, isnormal,issubgroup, mulperms, normalizer, orbit, parity,
permrep, pres, transgroup ]
Функции этого пакета представляют интерес для математиков, работающих в области конечных групп. Но вряд ли они будут полезны большинству пользователей. Тем не менее, наличие таких функций говорит о полноте функциональных возможностей системы Maple 7.
Пакет для работы с симметрией Ли liesymm
В этом пакете, являющемся реализацией алгоритма Харрисона-Эстабрука, имеется ряд функций:
> withCllesymm);
Warning, the protected name close has been redefined and unprotected
[ c£A,&mod, H,Lie, Lrank, TD, annul, autosimp, close, d, depvars, determine, dvalue, extgen, extvars, getcoeff, getform, hasclosure, hook, indepvars, makeforms, mixpar, prolong, reduce, setup, translate, vfix, wcollect, wdegree, wedgeset, wsubs]
Эти функции достаточно специфичны и могут пригодиться лишь узким специалистам.
Пакет команд для решения уравнений SolveTools
Пакет команд с весьма многообещающим названием SolveTools на самом деле содержит вовсе не средства для решения уравнений, а несколько весьма специфических функций:
> with(SolveTools):
[Basis, Complexity, GreaterComplexity, RationalCoefficients, SortByComplexity]
Функции этого пакета позволяют найти базис выражений, дескрипторы и рациональные коэффициенты. Примеры применения этого пакета очень просты, и с ними несложно ознакомиться. Однако при этом возникает вопрос «Зачем это надо?», который (увы!) остается без ответа.
Пакет для работы с таблицами Spread
Загрузка этого пакета дает средства для работы с таблицами:
> with(Spread);
{CopySelection, CreateSpreddsheet,, EvaluateCurrentSelection, EvahiateSpreadsheet,
GetCellFormula, GetCellVabe, GetFormulaeMatrix, GetMaxCok, GetMaxRows, GetSelection, GetValuesMatrix, lnsertMatrixIntoSelection , IsStale, SetCellFormula, SetMatrix, SetSelection]
Функции пакета не имеют самостоятельного значения и призвана поддерживать работу с электронными таблицами, которая уже была подробно описана. Они дают такие средства, как создание в документе шаблона таблиц, проведение операций по заполнению и редактированию ячеек таблиц, копированию содержимого таблиц в буфер памяти и т. д. Назначение функций достаточно очевидно из их составных имен.
Пакет codegen представляет собой набор команд, предназначенных для организации взаимодействия системы Maple 7 с другими программными средствами:
> with(codegen);
[С, GRAD, GRADIENT, HESSIAN, JACOB1AN, cost, declare, dontreturn, eqnjortran, homer, intrep2maple,joinprocs, makeglobal, makeparam, makeproc, makevoid, maple2intrep, optim ize, packargs, packlocals, packparams, prep2trans, renamevar, split, swapargs ]
Этот пакет очень полезен программистам, занимающимся разработкой сложных программных комплексов. Пакет позволяет создавать процедуры на языке Maple 7 и транслировать их в программные модули, записанные на других языках программирования, таких как Фортран или Си.
Пакет создания контекстных меню context
Пакет context служит для создания контекстных меню. Он содержит небольшое ' число функций:
> with(context):
[buildcontext, clearlabels, defaultcontext,
display, installcontext, restoredefault,
testactions, troubleshoot]
Этот пакет используется довольно редко и в основном пользователями, решающими в среде Maple не вычислительные, а системные задачи. Описание таких задач выходит за рамки данной книги.
Пакет организации многопроцессорной работы process )
Этот узкоспециализированный пакет содержит ряд функций по организации работы на нескольких процессорах:
> with(process):
[block, ey.ec, fork, kill, pclose, pipe, popen, wait ]
Данные функции представляют интерес для пользователей операционной системы UNIX, так что в проблематику данной книги не входят.
Пакет поддержки вычислений с размерными величинами Units
При выполнении большинства вычислений рекомендуется использовать безразмерные величины. Однако в некоторых областях науки и техники, например в физике, широко используются размерные величины, у которых помимо их значения указываются единицы измерения. Довольно развитую поддержку таких расчетов обеспечивает новый пакет расширения системы Maple 7 — Units. Он содержит следующие функции:
> with(Units);
[AddBaseUnit, AddDimension,AddSystem, AddUnit, Converter, GetDimension, GetDimensions, GetSystem, GetSystems, GetUnit, GetUnits, HasDimension, HasSystem, HasUnit, Natural, RemoveDimension, RemoveSystem, Standard, Unit, UseContexts, UseSystem, UsingContexts, UsingSystem]
Большинство функций этого пакета достаточно просты и даже очевидны. В связи с этим ограничимся несколькими характерными примерами их применения:

Пакет для работы с рядами ортогональных многочленов OrthogonalSeries
Новый пакет для работы с рядами ортогональных многочленов OrthogonalSeries имеет довольно представительный набор функций:
> with(OrthogonalSeries);
[Add, Apply Operator, ChangeBasis, Coefficients, ConvertToSum, Copy, Create, Degree, Derivate, DerivativeRepresentation, Evaluate, Getlnfo, Multiply, PolynomialMultiply, ScalarMultiply, SimplifyCoefficients, Truncate]
Поскольку этот пакет представляет интерес в основном для опытных математиков, мы не будем рассматривать его функции (в целом достаточно простые) подробно и ограничимся несколькими примерами. В следующем примере с помощью функции Create создается бесконечный ряд с ортогональным многочленом Эрмита в составе базового выражения ряда:

В другом примере показано представление полиномиального выражения в новом базисе с ортогональными многочленами Чебышева с помощью функции ChangeBasis:

Обратите внимание на то, что новое выражение после исполнения команды Evaluate приняло вид исходного выражения.
Следующий пример демонстрирует создание ряда на основе ортогональных многочленов Чебышева и его копирование с помощью функции Сору:
> S:=Create((-irn/n!,ChebyshevT(n,x));

Вычисление производной от ряда с ортогональными многочленами представлено ниже:

Еще один пример демонстрирует операцию скалярного умножения ряда с помощью функции ScalarMultiply:

Приведенные примеры показывают, что применение этого пакета достаточно просто. С деталями (порой довольно многочисленными) применения функций этого пакета можно познакомиться по справке на данный пакет.
Пакет поддержки стандарта MathML
Для представления математической информации на страницах Интернета в последние годы был создан специальный язык MathML. Пока для большинства пользователей MathML — просто «экзотика», но так как наряду с XML его поддерживает World Wide Web Consortium, его вынуждены поддерживать все солидные фирмы — причем не только создающие системы Компьютерной математики. Среди них такие крупные корпорации, как Intel, IBM и Microsoft. В Maple 7 предусмотрена новая возможность поддержки стандарта MathML 2.O. Для такой поддержки используются MathML Viewer (см. урок 2) и пакет MathML.
Пакет MathML дает минимальный набор функций для использования языка MathML:
> with(HathML);
[Export, ExportContent, ExportPresentation, Import, ImportContent]
В нем всего 5 функций, что позволяет разобрать их достаточно детально. Первые три функции служат для экспорта выражений:
Еще две функции служат для импорта строки в формате MathML и его преобразования в Maple-выражение:
Import(mnlstring) и ImportConterrt(mmlstnng)
Следующий пример наглядно иллюстрирует применение функций пакета расширения MathML для преобразования математического выражения а*х+b вначале в запись на MathML, а затем преобразование этой записи str в Maple-выражение:
> str:=MathML[Export]
( а*х + b );
str := "<math xmlns-http://www.w3.org/1998/Math/MathML'> <semanticsXmrow xrfe f='id5'xmrow xref='id3'xnii xref='idl '>a</mi><mo>⁢</moXml xref='id2'>x</mi></mrowxmo>+</mo><mixref='id4'>b</mi>
</mrowXannotati on-xml encodrag='MathML-Content'><apply id='id5'><plus/><apply id='id3'xtft mes/xci id='idl'> a</ci><ci id='id2'>x</cix/applyxci id='id4'>b</ci></apply>\ </annotation-xml> <annotationencoding='Maple'> a*x+b </annotationx/semantics\ ></math>" > Import(str):a x + b
Этот пример показателен тем, что дает представление о виде записей на языке MathML. Нетрудно заметить, что это достаточно громоздкий язык. Функции, представленные выше, автоматизируют процесс составления записей на языке MathML обычных математических выражений, что делает доступной для обычных пользователей подготовку публикации в Интернете, содержащей математические выражения.
В Maple 7 резко расширены средства интеграции с Интернетом. Это сделано не только на уровне специфических для математических приложений средств, таких как рассмотренный выше пакет MathML, но и на уровне обычных языков сети, таких как HTML и XML.
Пакет XMLTools служит для поддержки средств языка XML. Этот пакет предоставляет весьма внушительное число функций для этого:
> with(XMLTools):
[AddAttribute, AddCfiild, AttrCont, AttributeCount, AttributeNames, AttributeValue, AttributeValueWithDefault, Attributes, CData, CDataData, CleanXML, Comment,
CommentText, ConfentModel, ContentModelCount, Element,
ElementName, ElementStatistics,Equal, FirstChild, FromString, GetAttribute, GetChild, HasAttribute, HasChild,
IsCData, IsComment, IsElement, IsProcessinglnstruction,
IsTree, JoinEntities, LastChild, MakeElement, Print, PrintToFile, PrintToString, ProcessAttributes, ProcessingInstruction, ProcessinglnstructionData, ProcessinglnstructionName, ReadFile, RemoveAttribute, RemoveAttributes, RemoveChild, RemoveContent, SecondChild, Select Attributes, SelectContent, SelectRemoveAttributes, SelectRemoveContent, SeparateEntities, Serialize,
Strip Attributes, StripComments, SubsAttribute, SubsAttributeName, ThirdChild, ToString, WriteFile]
Рассмотрение этих средств (как и средств поддержки HTML) далеко выходит за пределы тематики данной книги, хотя многие из них достаточно просты. Поэтому ограничимся единственным примером применения функции Print для получения программы на языке XML соответствующей программе задания выражения, рассмотренного в предшествующем разделе:
> XMLTools[Print](К );
<math xmlns='http://www.w3.org/1998/Math/MathML1>
<semantics>
<mrowxref='id5'>
mrowxref='id3'>
<mixref='idl'>a</mi>
<mo>⁢</mo>
<mixref='id2'>x</mi>
</mrow> <mo>+</mo>
<mixref='ld4'>b</m1>
</mrow>
<annotation-xml encoding='MathML-Content'>
apply id='id5'>
<plus/>
<apply id='id3'>
<times/>
<ci id='idl'>a</ci>
<ci id='id2'>x</ci>
</apply>
<cild='id4'>b</ci>
</apply>
</annotation-xml>
<annotat1on encoding='Maple'>a*x+b</annotation>
</semantics>
</math>
Пакет создания внешних программ ExternalCalling
Пакет ExternalCalling служит для создания внешних программ, записанных на языке Maple (или C++). Состав пакета представлен небольшим числом функций:
Детальное знакомство с этим пакетом мы опускаем. Заинтересованный читатель найдет нужные сведения в справке по этому пакету.
Пакет линейных операторов Linear-Operators
Пакет линейных операторов LmearOperators — новый пакет, содержащий средства для работы с линейными операторами. Состав пакета виден из его вызова:
> with(LinearOperators);
[Apply, DEToOrePoly, FactoredAnnihilator, FactoredGCRD,
FactoredMinimalAnnihilator,FactoredOrePolyToDE, FactoredOrePolyToOrePoly, FactoredOrePolyToRE, IntegrateSols, MinimalAnnihilator, OrePolyToDE, OrePofyToRE, REToOrePoly, dAlembertianSolver}
Набор функций пакета достаточно представителен. Но, поскольку область применения пакета весьма специфична, рекомендуется знакомиться с его возможностями по справкам на его функции и обзорной статье по нему, имеющейся в обзоре новых пакетов расширения Maple 7 (также размещенной в справочной базе данных пакета).
Пакет для работы со случайными объектами RandomTools
Пакет для работы со случайными объектами RandomTools служит для расширения базовых возможностей системы Maple 7 (для большинства пользователей и так вполне достаточных) в части генерации различных случайных объектов, таких как числа различных форматов, векторов, матриц, строковых символов, таблиц и т. д. Они образно названы Flavor (в буквальном переводе «букет (вина)»), что подчеркивает возможную сложность структуры создаваемых объектов.
Пакет представлен небольшим числом основных функций:
> with(RandomTools);
[AddFlavor, Generate, GetFlavor, GetFlavors, HasFlavor, RemoveFlavor]
Однако функции AddFlavor и Generate могут использоваться с внушительным набором типов случайных объектов:
|
Choose |
complex |
exprseq |
float |
identical |
|
Integer |
list |
listlist |
negative |
negint |
|
Nonnegative |
nonnegint |
nonposint |
nonpositive |
nonzero |
|
Nonzeroint |
polynom |
posint |
positive |
rational |
|
Set |
structured |
truefalse |
|
|
Действие большинства из них вполне очевидно из названий. Основной функцией является функция генерации случайных объектов Generate(expr). Если тип объекта не задан (например, функцией AddFlavor), то использование функции Generate будет порождать сообщение об ошибке. Примеры применения функций представлены ниже:
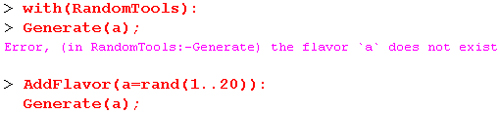

Функция GetFlavor(flvr) представляй случайный объект (или объекты) в форме процедуры:
> AddF1avor(a = rand(1..20)):
Generate(a):
15
> GetFlavor(a);
procO localt; global_seed;
_seed := irem(ax_seed,p);
t :=_seed;
toconcats do_seed:=irem(ax_seed,p);
t := sxt + _seed end do ;
irem(t, divisor) +offset endproc
> GetFlavor(integer);
module () localDefaults;
exportMain;
end module
Другая функция GetFlavors () возвращает все типы случайных объектов:
> GetFlavorsO;
a, alphachar, choose, complex, exprseq, float, integer, list, listlist, negative, negint, nonnegative, nonnegint, nonposint, nonpositive, nonzero, nonzeroint, polynom, posint, positive, rational, set, string, truefalse
Функция HasFlavor(flvr) служит для проверки наличия объекта данного типа в списке типов объектов, а функция RemoveFl avor(f1vr) — для удаления типа объекта. Следующие примеры иллюстрируют применение этих функций:
> HasFlavor(a):
true
> RemoveFlavor(a);
> HasFlavor(a):
false
> GetFlavors();
alphachar, choose, complex, exprseq, float, integer, list, listlist, negative, negint, nonnegative, nonnegint, nonposint, nonpositive, nonzero, nonzeroint, polynom, posint, positive, rational, set, string, truefalse
Обратите внимание на то, что после уничтожения объекта типа а он исчез из списка, выводимого функцией GetFlavors. Этот пакет, несмотря на довольно специфические возможности, наверняка будет полезен тем читателям, которые всерьез заняты реализацией «продвинутых» методов Монте-Карло, основанных на моделировании случайных объектов и ситуаций. Он служит серьезным дополнением к пакету статистических расчетов stats, описанному в этом уроке выше.
Пакет для работы со списками ListTools
Новый пакет ListTools содержит ряд полезных команд для работы со списками. Их набор представлен ниже:
> with(ListTools):
Warning, the assigned name Group now has a global binding
[BinaryPlace, BinarySearch, Categorize, DotProduct, FindRepetitions, Flatten, FlattenOnce, Group, Interleave, Join, JoinSequence, MakeUnique, Pad, PartialSums, Reverse, Rotate, Sorted, Split, Transpose ]
Пакет содержит набор известных функций для работы со списками, например скалярного умножения списков, их обращения, транспонирования, поворота, объединения и т. д. Ограничимся примером на вычисление скалярного произведения векторов:
> L := [0., .84, .91, .14, -.76, -.96, -.28, .66, .99, .41, -.54]:
L := [0., .84, .91, .14, -.76, -.96, -.28, .66, .99, .41, -.54]
> М := [1., .54, -.42, -.99, -.65, .28, .96, .75, -.15, -.91, -.84];
М:= [ 1., .54, -.42, -.99, -.65, .28, .96, .75, -.15, -.91, -.84]
> DotProduct(L, L):
5.0063
> DotProduct(L, M):
.3162
Другие новые пакеты, CurveFitting и LinearFunctionalSystem, мы рассмотрели ранее достаточно подробно (см. уроки 14 и 15). В целом надо отметить, что состав пакетов Maple 7 существенно расширен по сравнению с предшествующими версиями системы. В то же время все пакеты, вошедшие в состав Maple 6, сохранены в новой версии программы — Maple 7, что гарантирует полную совместимость с ней. Практически это было подтверждено проверкой всех (а их многие сотни) примеров применения системы Maple 6 применительно к новой версии Maple 7.
В этом уроке мы научились:
|
|