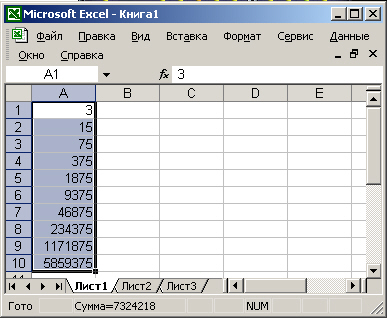
Excel выполняет вычисления последовательно, но некоторые операции имеют более
высокий приоритет и выполняются раньше других:
1. Возведение в степень и выражения в круглых скобках.
2. Умножение и деление.
3. Сложение и вычитание.
Технические возможности Excel позволяют создавать достаточно сложные формулы.
Однако подлинная мощь Excel как программного средства реализуется через широкий
набор встроенных функций, предназначенных для выполнения самых различных вычислительных
и логических процедур.
Несмотря на их разнообразие, все функции имеют одинаковый стандартный формат:
имя функции и находящийся в круглых скобках перечень аргументов, разделенных
точками с запятой. Например:
=ОКРВВЕРХ(ВЗ;2).
Существенную помощь пользователю в процессе конструирования выражений, содержащих
формулы, может оказать Мастер функций. Вызвать его можно одним их следующих
способов:
- меню Вставка > Функция;
- кнопка Вставка функции на панели Стандартная.
В Excel редактирование формул производится так же, как и редактирование любых
введенных данных:
- выделить ячейку, содержащую редактируемую формулу, нажать клавишу F2, внести
изменения, нажать клавишу Enter;
- быстрая правка - двойной щелчок по ячейке, нажать клавишу F2, внести изменения,
нажать Enter.
Копируются формулы так же, как и другие данные:
- выделить ячейку, меню Правка > Копировать (или комбинация клавиш Ctrl+C);
выделить целевую ячейку (ячейки), то есть область, куда надо поместить копируемые
данные; меню Правка > Вставить (или Ctrl+V);
- быстрое копирование: выделить ячейку, содержащую формулу, и перетащить границу
выделенной ячейки в новое место, удерживая нажатой клавишу Ctrl.
Принципиальным при копировании и перемещении формул является вопрос о преобразовании
содержащихся в них ссылок на другие ячейки. Очевидно, что в зависимости от внутренней
логики выражений в определенных случаях адреса должны оставаться неизменными,
а в других ситуациях для пользователя будет более удобным и предпочтительным,
чтобы их пересчитали с учетом относительного изменения местоположения. Для решения
данной задачи в процессорах электронных таблиц поддерживается система относительных
и абсолютных ссылок. Абсолютная ссылка - это не изменяющийся при копировании
и перемещении формулы адрес ячейки, содержащий исходные данные. В качестве признака
абсолютной ссылки в адресе используется знак $. Различают:
o полную абсолютную ссылку (знак $ ставится и перед именем столбца, и перед
номером строки, например $А$8). В этом случае при копировании и перемещении
адрес ячейки не меняется;
o частичную абсолютную ссылку (знак $ ставится либо перед номером строки, либо
перед именем столбца, например А$8 или $А8. В данном случае при копировании
и перемещении неизменной остается только одна из координат).
Для быстрого изменения типа адресации в формулах используется функциональная
клавиша F4 (при ее последовательном нажатии вид адреса, находящегося в строке
ввода данных, попеременно меняется с относительного на абсолютный, с абсолютного
на частично абсолютный и т. д.).
Обратим внимание на то, что при работе с экономическими приложениями к необходимости
применения абсолютной адресации пользователь приходит, если так можно выразиться,
естественным путем. В качестве хрестоматийного примера в литературе обычно приводится
задача расчета заработной платы с помощью электронных таблиц, где в формулах
для суммы налога содержится абсолютная ссылка на ячейку, содержащую ставку налогообложения.
В случае относительных ссылок при копировании и перемещении формул происходит
пересчет адресов ячеек, на которых они указывают, с учетом относительного изменения
места этих формул на листе. Как нетрудно заметить, по умолчанию используется
именно относительная адресация.
Реально идет речь о том, что релятивистские формулы не соответствуют астрономическим наблюдениям, давая на порядок и более меньшую массу и меньшую энергию. Отсюда сделан фокуснический вывод, что есть "темная материя" и "темная энергия", но не вывод, что релятивистские формулы не соответствуют реалиям. Подробнее читайте в FAQ по эфирной физике.
|
|
 |