Николаев Г. В.
Однако вернемся теперь в наше время Если принять во внимание, что в настоящее время считается уже вполне достоверным существование особой среды физического вакуума и что описываемые свойства физического вакуума (электрические Е0, магнитные μ0, поляризуемости, квантуемости и т. д.) вполне соответствуют свойствам среды электромагнитных полей, то является вполне очевидным настоятельная необходимость вновь вернуться к исходной модели уравнений электродинамики, чтобы они вновь могли обрести свою первоначальную физическую сущность. Для совершенствования же уравнений электродинамики, как становится теперь очевидным, остается только окончательно ввести в них, прежде всего, физический принцип близкодействия и получить непротиворечивую систему дифференциальных уравнений электростатики и полную систему дифференциальных уравнений электродинамики для двух типов магнитных полей HT = rot A и H|| = –div A, выразив их теперь уже, в соответствии с принципом близкодействия, только через одни токи смещения. И этого оказалось вполне достаточно, чтобы сразу же исчезли практически все рассмотренные выше противоречия и парадоксы в интерпретации реально наблюдаемых явлений электромагнетизма. Исчезла при этом и большая часть трудностей и противоречий в теоретическом обосновании исходных представлений законов электромагнетизма. Законы электродинамики оказались теперь в полном соответствии и с фундаментальными законами механики. Для устранения же остающихся противоречий оказывается необходимым еще несколько уточнить наши представления о механической, электромагнитной и гравитационной массе, о деформации электрических полей движущихся зарядов, о природе кинетической энергии движущегося заряда и т. д. Последовательность совершенствования уравнений электростатики и электродинамики может заключаться, например, в следующем.
1. Основываясь на представлении существования среды физического вакуума [23], установлена существенная ограниченность классических и релятивистских представлений электродинамики в условиях реального околоземного пространства [24, 33—38]. Из рассмотрения как механических, так и электромагнитных явлений в условиях реального пространства и из общего сопоставительного анализа накопленного до настоящего времени экспериментального материала в области оптики и электродинамики сделан вывод о несоблюдении принципа относительности для законов механики, оптики и электродинамики в реальном физическом пространстве и возможности его выполнения только в некоторых локальных областях и только для физически эквивалентных систем отсчета. Учет связи инерциальных систем с массивными гравитирующими телами и гравитационными полями, без которых немыслимо существование реального пространства, приводит к необходимости отказа от принципа относительности как фундаментального принципа. Законы механики, электродинамики и оптики остаются справедливыми и не изменяют своего вида только для физически равноценных инерциальных систем. Уравнения же механики, электродинамики и оптики могут быть инвариантными только в абсолютно пустом не физическом пространстве, так как ни одна точка реального физического пространства не может находиться одновременно в одинаковых физических условиях в двух разных движущихся относительно друг друга системах, даже если эти системы являются инерциальными и физически равноценными. Нахождение уравнений движения материальных частиц, электрических и магнитных полей в какой-либо одной системе координат физически реального пространства из соответствующих уравнений движения, электрических и магнитных полей другой системы возможно только при учете степени физической равноценности рассматриваемых систем отсчета. Оптическая и электродинамическая асимметрия реального околоземного и космического пространства обусловлена свойствами физического вакуума реального пространства и его связью с гравитационными полями массивных гравитирующих систем [61].
2. С учетом электромагнитных свойств физического вакуума реального околоземного пространства [64—71] установлена функциональная взаимосвязь напряженности электрического поля E(r) в точке наблюдения r, индуцируемого покоящимся в лабораторной системе на поверхности Земли зарядом e(r'), с поверхностной плотностью σ0(r) поляризационных зарядов вакуумной среды в этой же точке г, что находится в полном соответствии с физическим принципом близкодействия [70]
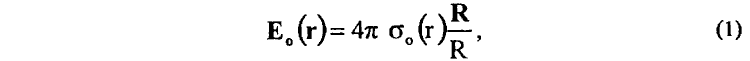
где
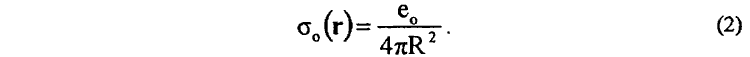
Поляризационный заряд e0 = e вакуумной среды на поверхности сферы, окружающей заряд e и пересекающей точку наблюдения r, определяется из условия применимости к электрическому полю E(r) покоящегося заряда e(r') теоремы Остроградского-Гаусса.
3. Определен закон электростатического взаимодействия заряда e2 с электрическим полем E01 (1) заряда e1 (закон Кулона) в среде физического вакуума, отражающий физический принцип близкодействия
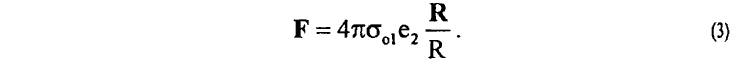
4. Энергия WE электрического поля E0 (1) заряда e в реальном пространстве получает тривиальную интерпретацию как работа поляризации среды физического вакуума
Выражение (4) полностью эквивалентно известному выражению для энергии W'E электрического поля Е заряда, записываемого в виде
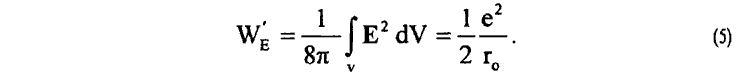
5. Энергия взаимодействия U электрических зарядов e1 и e2 определяется легко интерпретируемой, с физической точки зрения, работой поляризации среды физического вакуума в перекрестных электрических полях E01 и E02
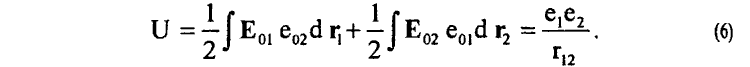
Выражение (6) эквивалентно известному выражению для энергии взаимодействия электрических полей E1 и E2 зарядов e1 и e2
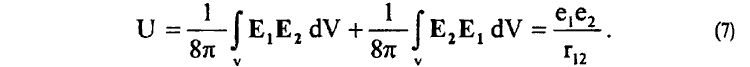
6. Найдена непротиворечивая система дифференциальных уравнений для электрического поля E0 (1) в точке наблюдения r, отражающая физический принцип близкодействия [70]
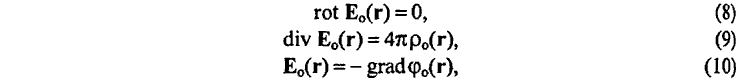
где ρ0(r) — плотность поляризационных зарядов вакуумной среды в точке наблюдения r, определяемая зависимостью
Система уравнений (8)—(10) легко приводится к уравнению Пуассона, в решении которого уже не используется математический формализм штрихованных координат и δ-функции.
7. Основываясь на представлении реальности существования токов смещения jсм в среде физического вакуума около движущегося заряда
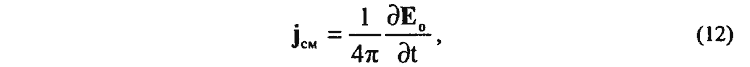
установлена их функциональная взаимосвязь с индуцируемыми по принципу близкодействия этими токами магнитными полями HT и H||: [10, 15, 16, 21, 22, 25, 26, 50, 72—78]
где
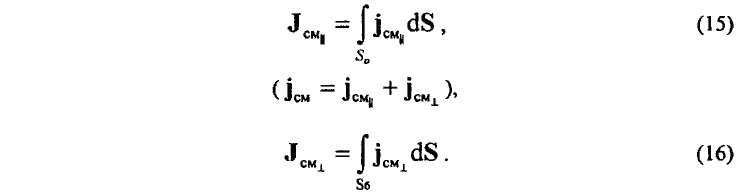
Поверхность S0 ограничивает аксиальный поток тока смещения Jсм|| (15). На её внешней поверхности отыскивается напряженность магнитного поля HT (13). Поверхность Sδ ограничивает радиальный поток тока смещения JсмT (16). На её внешней поверхности отыскивается напряженность магнитного поля H|| (14).
8. Через однозначную величину физического параметра векторного потенциала А движущегося заряда e (V<<C),
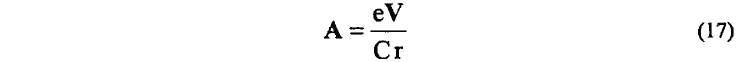
устанавливается существование в пространстве около него двух типов магнитных полей — векторного HT и скалярного H|| [22, 73]
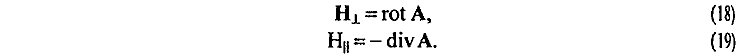
При определении результирующего векторного магнитного поля H°T = rot A0 от отрезка линейного тока, направление вектора поля HT определяется положением точки наблюдения N справа или слева от направления тока в отрезке и не зависит от направления тока в нём в сторону к точке наблюдения N или от нее. При определении же результирующего скалярного магнитного поля H°|| = –div A0 от отрезка линейного тока знак поля H°||, наоборот, не зависит от положения точки наблюдения справа или слева от направления тока в отрезке, но зато зависит от направления тока в нём в сторону к точке наблюдения N или от неё. Если при этом отрезок тока дополнительно меняет еще и свое направление на 90° по отношению к первоначальному, то знак у скалярного магнитного поля H°|| меняется еще раз. С учетом этих особенностей результирующее скалярное магнитное поле H°|| около любого замкнутого (например прямоугольного) контура равно нулю только в плоскостях, каждая из которых проходит через середину стороны прямоугольного контура и перпендикулярна ей. На углах же его результирующее скалярное магнитное поле H°|| имеет максимальное значение
обусловливая появление так называемых "угловых эффектов" динамического взаимодействия, например, с элементами других контуров с токами (см. описания опытов 4, 13, 20, 21, 25—28).
9. Найдена полная функциональная взаимосвязь напряженности электрического поля E0 движущегося заряда с двумя типами индуцируемых им магнитных полей
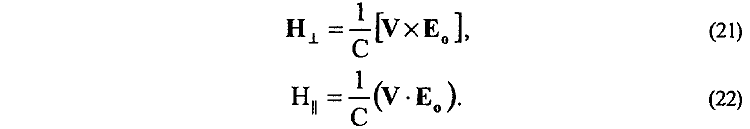
10. Установлена функциональная взаимосвязь для полного магнитного взаимодействия произвольно движущихся зарядов e1 и e2 [15]
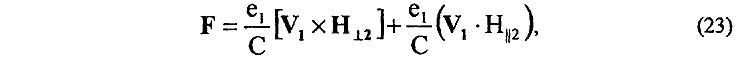
согласно которой магнитное взаимодействие параллельно движущихся зарядов e1 и e2 определяется потенциальной частью зависимости (23)
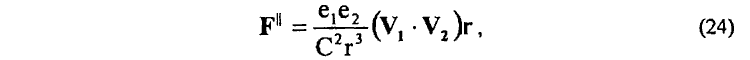
между тем как магнитное взаимодействие перпендикулярно движущихся зарядов e1 и e2 определяется непотенциальной частью зависимости (23)
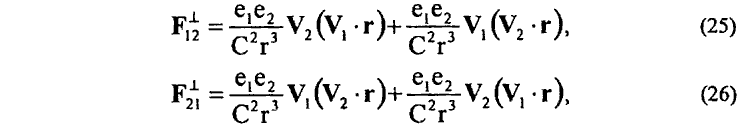
причем
Зависимости (23)—(26), в противоположность формулам Лоренца и Ампера, не противоречат третьему закону механики, согласуются с экспериментальными наблюдениями и устанавливают существование неизвестного ранее явления продольного магнитного взаимодействия.
11. Согласно (13), (14), (18), (19), (21), (22) для полной энергии магнитных полей HT и H|| движущихся зарядов e1 и e2 можно записать
где
что полностью эквивалентно энергии WA°, определяемой известной зависимостью через векторный потенциал А [13]:
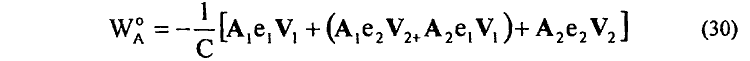
Зависимости (23) и (28) легко устраняют известные в электродинамике многочисленные противоречия и парадоксы (см. теоретические противоречия 7—10, 12—16, 19).
12. Из (28)—(30) для полной энергии магнитного взаимодействия WH параллельно движущихся зарядов e1 и e2 находим
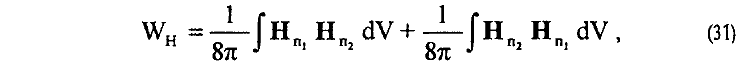
что эквивалентно энергии взаимодействия WA , определяемой известной зависимостью через векторный потенциал А [13]
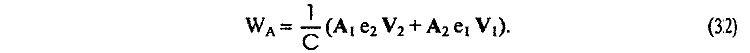
13. Сила F|| (24) магнитного взаимодействия параллельно движущихся зарядов e1 и e2 может быть определена так же как
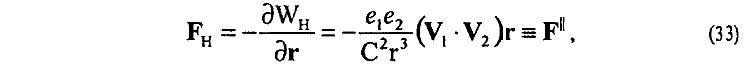
что эквивалентно известной потенциальной зависимости (см. теоретические противоречия 12, 13, 14, 15)
14. Установлено существование системы градиентных электрических полей произвольно движущегося заряда [16, 74]
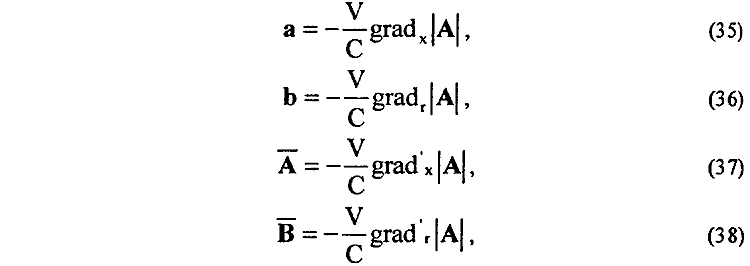
определяющих полную силу F (23) магнитного взаимодействия между двумя произвольно движущимися зарядами e1 и e2 как
Из (35)—{38) непосредственно устанавливаем, что любые так называемые "магнитные" взаимодействия (в том числе через скалярное магнитное поле) представляют собой, в конечном счете, взаимодействие через градиентные электрические поля, которые отражают собой как бы учет запаздывающих потенциалов и деформации электрических полей движущихся зарядов. Однако зависимость (39) для взаимодействия движущихся электрических зарядов через градиентные электрические поля a, b, A, B рассматривается в традиционной в электродинамике схеме как дополнение к неизменному кулоновскому взаимодействию между этими же зарядами. Физический же смысл градиентных электрических полей (35)—(38) движущегося заряда заключается в том, что если их рассматривать совместно с кулоновским электрическим полем EK этого же заряда, то результирующее электрическое поле E движущегося заряда будет представлять собой не что иное, как обычное деформированное электрическое поле E' = Eдеф, обусловленное учетом тривиальных эффектов запаздывающих потенциалов.
15. Полная энергия магнитных полей HT и H|| движущегося со скоростью V заряда e электрона оказывается равной [25]
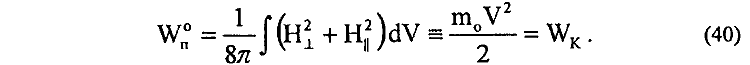
Из (40) следует вывод, что масса электрона полностью электромагнитного происхождения и гравитационными свойствами электрон (позитрон) не обладает.
16. Установлена полная функция Лагранжа для двух взаимодействующих заряженных частиц
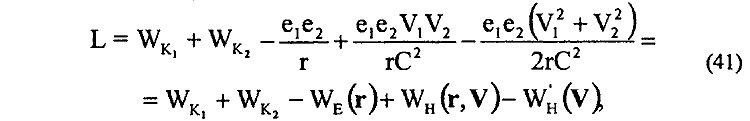
с помощью которой для закона сохранения обобщенного импульса Р находим
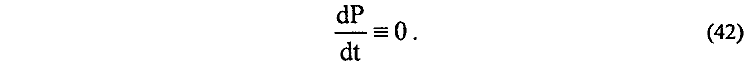
Известная в электродинамике функция Лагранжа дополнена членом e1e2(V12 + V22)/2rC2, который отражает собой не учитывавшуюся ранее непотенциальную часть магнитного взаимодействия между движущимися зарядами и является функцией только от скорости движения зарядов.
17. Получена циклически замкнутая (отражающая физический принцип близкодействия) система дифференциальных уравнений для двух типов магнитных полей HT и H|| движущегося в физическом вакууме заряда [22]
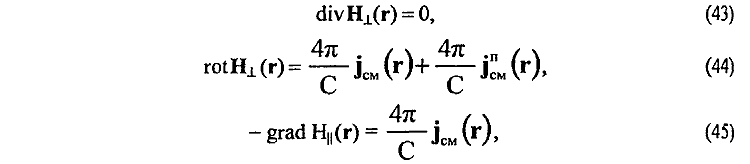
где
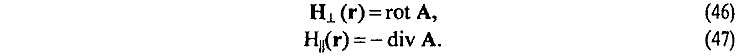
Система уравнений (43)—(47) легко (без использования так называемых дополнительных условий, калибровок) приводится к уравнению Пуассона, решение которого находится уже без использования математического формализма штрихованных координат и δ-функции. В случае линейных отрезков тока решение уравнений (43)—{45) может быть легко найдено простым интегрированием правых и левых частей уравнений по поверхностям S0 и Sσ, ограничивающих соответственно аксиальные Jсм|| (15) и радиальные JсмT.(16) токи смещения.
В частном случае линейного бесконечного тока система уравнений (43)—(47) сводится к системе уравнений для одного векторного магнитного поля HT аналогичной известной системе уравнений Максвелла.
18. Получена [73] полная система дифференциальных и интегральных уравнений для вихревого электрического поля A
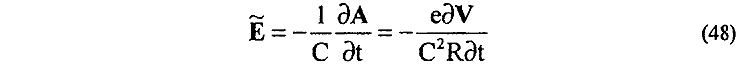
ускоренно движущегося заряда е в виде
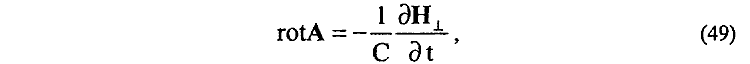
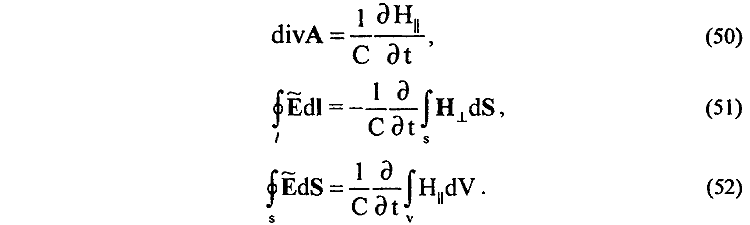
19. Установлена взаимосвязь вихревого электрического поля A (48) ускоренно движущегося заряда e с изменением полной энергии WП (40) двух типов магнитных полей HT и H|| этого же заряда [15]
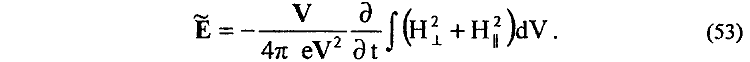
20. Установлено, что работа А в собственном вихревом электрическом поле A (48) ускоренного до скорости V заряда e оказывается равной полной энергии WП (40) магнитных полей HT и H|| этого заряда [15]
Из (54) следует, что при ускорении, например, электрона (позитрона) до скорости V работа А (54) ускорения заряда e затрачивается только на создание магнитных полей HT и H|| этого заряда электрона, а не на придание так называемой кинетической энергии массе m0 заряда электрона.
21. Полная работа A0 двух взаимодействующих ускоряемых до скоростей V1 = V2 = V зарядов e1 и e2 в собственных вихревых электрических полях
A1 и A2 оказывается равной полной собственной энергии WH (40) и полной энергии W (31), (32) взаимодействующих магнитных полей HT и H|| этих зарядов [50]
что эквивалентно WH° (28) и WA° (30).
22. Установлена полная и симметричная система дифференциальных уравнений для вихревых электрических и вихревых магнитных полей и вихревых векторных потенциалов электромагнитного поля в физическом вакууме реального пространства [26, 75—77]
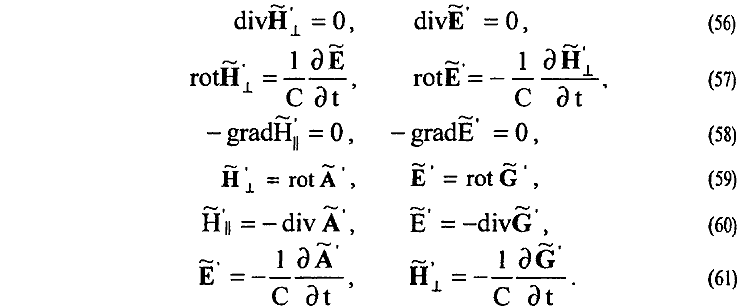
Система уравнений (56)—(61) легко (без использования так называемых нормировок, калибровок) приводится к волновым уравнениям для вихревых векторных потенциалов A' и G
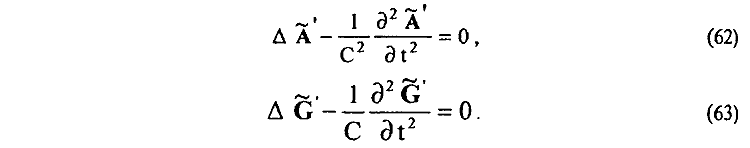
Дифференцированием левых и правых частей уравнений (62), (63) с учетом (59), (60) получаем соответствующие волновые уравнения для вихревых магнитных A'T и A' и вихревых электрических A' , A' полей в физическом вакууме реального пространства
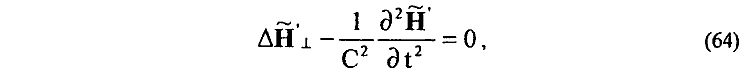
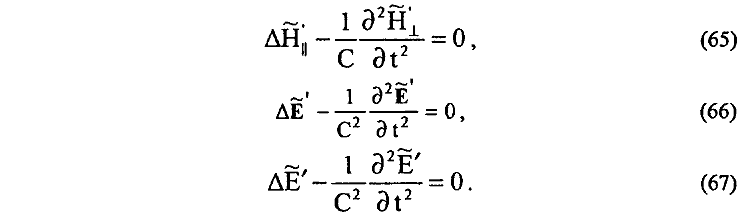
23. В рамках формализма векторного HT = rot A и скалярного H|| = –div A магнитных полей установлена функциональная зависимость для бесконечного циклического процесса зарождения и распространения электромагнитной волны ускоренно движущегося заряда, отражающая физический принцип близкодействия и естественную причинно-следственную связь между разными по своей природе токами и разными по своей природе электрическими и магнитными полями и потенциалами:
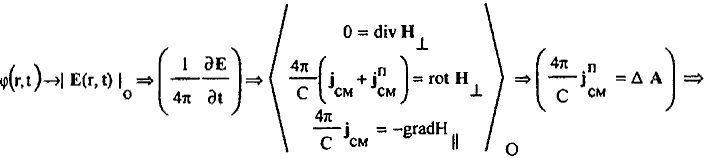
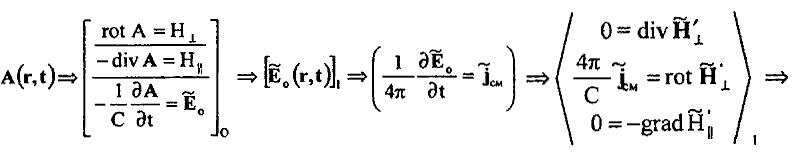
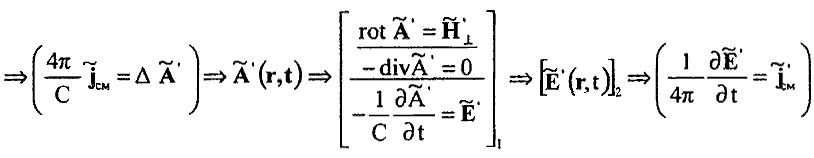
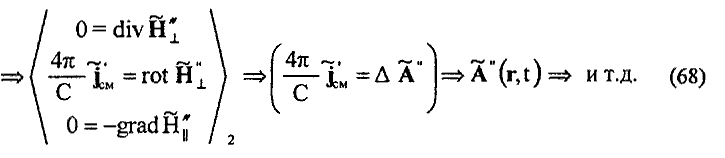
Начиная с 3-го цикла, вихревые электрические A" и вихревые магнитные A" и A" поля оказываются уже полностью эквивалентными вихревым электрическим A' и вихревым магнитным A', A' полям предыдущего 2-го цикла электромагнитной волны, что отражает собой начало распространения уже циклической электромагнитной волны.
24. Бесконечная функциональная зависимость (68) для процесса зарождения и распространения электромагнитной волны представляет собой, с физической точки зрения, достаточно наглядную картину причинно-следственной связи разных по своей природе явлений электромагнетизма, однако с математической точки зрения является весьма громоздкой и неудобной для практического пользования. Для придания зависимости (68) законченного математического вида волнового уравнения (62) достаточно уже повторяющийся, начиная со второго цикла, бесконечный циклический процесс просто зациклить, для чего необходимо в систему дифференциальных уравнений, например 3-го цикла,
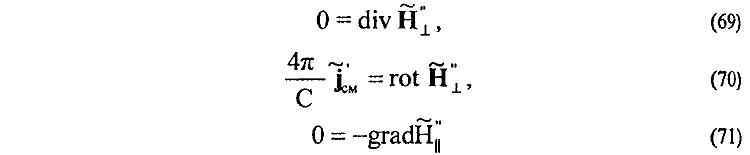
вместо отыскиваемых неизвестных магнитных полей AT", AT", электро-магнитного поля подставить известные уже значения этих полей AT', AT', найденные из решения системы уравнений предыдущего второго цикла, т. е.
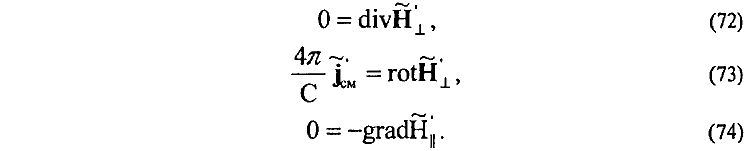
С учетом
из зацикленной системы дифференциальных уравнений (72)—(74), без использования математического формализма нормировок и калибровок, непосредственно устанавливаем
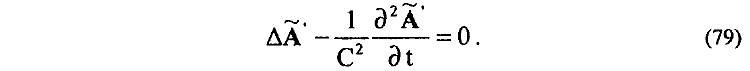
Таким образом, путем проведенного совершенствования уравнений электродинамики устранены основные серьезные противоречия и получены более или менее непротиворечивые, с физической и математической точек зрения, системы дифференциальных уравнений электростатики и электродинамики для двух типов магнитных полей Казалось, можно было бы торжествовать! Однако дальнейшие исследования показывают, что новая "совершенная" электродинамика оказывается все же недостаточно совершенной. Прежде всего, допущение существования двух типов магнитных полей — векторного HT и скалярного H||, разрешая многочисленные трудности и противоречия в экспериментальных и теоретических вопросах современной электродинамики, в некоторых частных случаях вновь приводит к новым трудностям и противоречиям. Например, при установлении зависимости для магнитных полей HT и H|| через токи смещения JсмT (15), Jсм|| (16) принцип близкодействия используется лишь частично (токи смещения JсмT , Jсм|| приходится определять через заданные поверхности S0 и Sσ). Более серьезные трудности обнаруживаются, например, при попытках отыскания энергии магнитного взаимодействия W между движущимися зарядами через их магнитные поля HT и H||, так как остается непонятной физическая сущность взаимодействия векторного HT и скалярного H|| магнитных полей между собой. И, наконец, в рамках формализма двух типов магнитных полей возникает принципиальная трудность при попытках установить физическую взаимосвязь между энергией магнитных полей и работой поляризации физического вакуума так же, как оказалось возможным в случае электростатики (4), (6). Обнаруженные трудности вынуждают искать пути дальнейшего совершенствования уравнений электродинамики. И такие пути совершенствования оказываются вполне возможными. От формализма двух типов магнитных полей — векторного HT и скалярного H|| — можно перейти, например, к формализму одного полного векторного магнитного поля HП (29). Новый формализм позволяет записать уравнения электродинамики уже в более простом и совершенном виде:
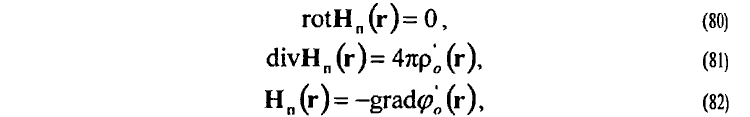
полностью эквивалентном уже записи уравнений электростатики (8}—(10), где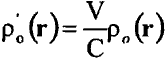 
и 
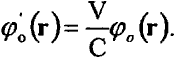
Получена соответствующая полная система дифференциальных уравнений и для переменных вихревых электромагнитных полей в физическом вакууме и соответствующая функциональная циклическая зависимость для процесса зарождения и распространения электромагнитной волны. В решении более совершенной системы уравнений электродинамики (80)—(82) принцип близкодействия используется уже полностью. Не возникает трудностей в определении энергии магнитного взаимодействия W (31), (32) и полной энергии магнитных полей (28), (30). Однако по-прежнему не удается найти функциональную взаимосвязь между энергией магнитных полей W (28) и работой поляризации физического вакуума. Последнее обстоятельство вынуждает обратиться к еще одному формализму выражения магнитных свойств движущихся зарядов — к градиентным электрическим полям (35)—(38), для которых, в частности, можно еще записать
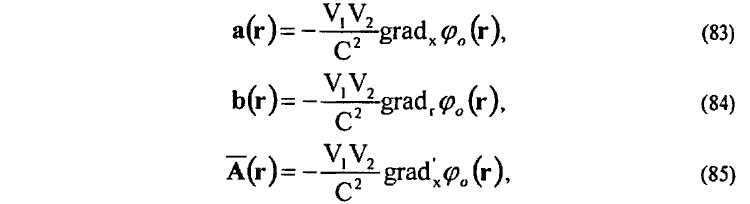
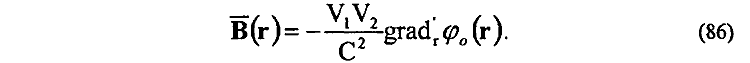
При группировке их в градиентные электрические поля E||
и ET для параллельно и перпендикулярно движущихся зарядов в виде
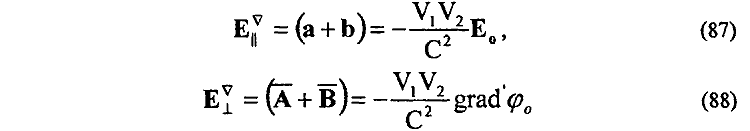
для полной энергии этих полей WE устанавливается уже непосредственная взаимосвязь с работой поляризации физического вакуума
что полностью эквивалентно энергиям WH° (28), WA° (30), A0 (54):
Таким образом, пути совершенствования привели нас, в конце концов, к тому,
что устранены практически все серьезные противоречия в считавшемся
"законченном здании" современной электродинамики, однако и на данном
этапе вряд ли можно считать это "здание" электродинамики полностью
законченным. Но наиболее удивительным результатом совершенствования
оказался неожиданный вывод, что для непротиворечивого отражения
физической сущности законов электромагнетизма необходимо полностью
отказаться от любых понятий "магнитного поля" как некой самостоятельной
физической сущности, так как градиентные электрические поля E|| и ET по своей природе представляют собой не что иное, как деформированную часть электрического поля движущегося заряда.
Логический
анализ сложившейся в электродинамике ситуации вновь привел нас к
выводу, что для определения сил взаимодействия движущихся в физическом
вакууме реального пространства электрических зарядов вполне достаточно
учесть деформацию электрических полей этих зарядов, обусловленную
тривиальными эффектами запаздывающих потенциалов. Завершив
весьма длительное кругосветное путешествие в необъятном океане
классической электродинамики и благополучно миновав все его каверзные
непредвиденные случайности и опасные подводные рифы, мы, к нашему
удивлению, вновь вернулись практически вплотную к тем исходным
"примитивным", в рамках современной электродинамики, представлениям о
законах электрического и магнитного взаимодействия, которые на заре
развития начальных представлений об электромагнетизме стояли перед
физиками того времени. Остается
только удивляться прозорливости Ампера, который предупреждал, что если в
электродинамике не отказаться от понятия "магнит", то в дальнейшем это
грозит неимоверной путаницей в теории...
Следовательно, пути совершенствования привели нас к необходимости сделать, наконец, последний и наиболее ответственный шаг и полностью отказаться от формализма любых видов магнитных полей и их аналогов. Тем более что из проведенного выше анализа просматриваются уже некоторые контуры новой электродинамики статических и динамических электрических полей. Например, если в уравнениях для полей E0 (8)—(10) и HП (80)—(82) физического вакуума реального пространства объединить статическое электрическое поле E0 с векторным полным магнитным полем HП в виде зависимости
то система дифференциальных уравнений электростатики и электродинамики принимает компактный вид общей системы дифференциальных уравнений для динамического электрического поля ЕД:
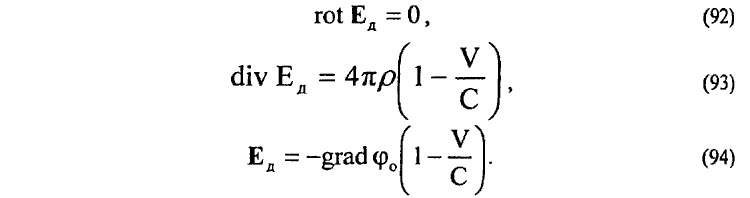
Наиболее интересным в этой системе дифференциальных уравнений является тот факт, что статическое и динамическое состояния электрических полей Е0 и ЕД в этой системе определяются простым динамическим коэффициентом (1 - v/c). В статическом состоянии (V = 0) система уравнений (92)—(94) описывает обычные электрические поля покоящихся зарядов, в динамическом же (V <> 0) система уравнений (92)—(94) в полной мере определяет все поля (91) движущихся зарядов. Однако, с другой стороны, полученная форма записи для динамического электрического поля EД (91) оказывается в значительной степени странной, так как простое умножение этого поля на покоящийся или движущийся электрический заряд не определяет силы взаимодействия этого заряда с динамическим электрическим полем EД. Для определения сил взаимодействия динамического электрического поля EД с покоящимся или движущимся электрическим зарядом оказываются необходимыми дополнительные формальные математические операции. Эти обстоятельства свидетельствуют, возможно, о том, что необходимо либо дальнейшее выяснение физической сущности динамического электрического поля EД (91), либо поиски других путей для формального отражения записи динамического электрического поля движущихся зарядов. В качестве динамического электрического поля EД движущегося заряда в аналогичном приближении можно рассмотреть, например, деформированное электрическое поле Е' (20) (см. стр. 31).
о котором упоминалось во 2-й части данного обзора. Динамическое электрическое поле в таком виде Е0' (95) обладает уже преимуществами, так как позволяет определять силу взаимодействия с ним покоящихся и движущихся электрических зарядов. Кроме того, дифференциальная система уравнений для динамического электрического поля Е0' (95) в аналогичной записи
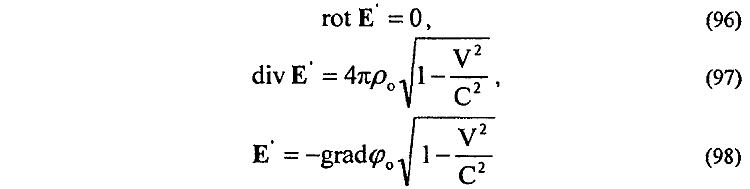
имеет те же преимущества, определяя
статическое и динамическое состояния электрического поля, но уже
несколько иным динамическим коэффициентом
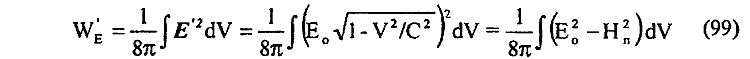
выявляется интересная физическая сущность этого поля. Из (99), в частности, следует, что начальная энергия WE0 электрического поля покоящегося заряда уменьшается при движении этого заряда, причем на величину, как раз равную энергии формально выявляющегося полного магнитного поля НП. То есть действительная физическая сущность энергии WH магнитного поля заключается в том, что эта энергия в пространстве около движущегося заряда не появляется, как это общепринято считать, а исчезает из него [23]. Весьма кстати здесь вспомнить высказывание А. Пуанкаре, который отмечал в свое время, что "характерная особенность электрического тока заключается в том, что энергия магнитного поля "втекает" в проводник", т.е. исчезает из окружающего проводник пространства. Обнаруживается еще ряд других интересных следствий представления о динамическом электрическом поле Е'0 (95). Например, если рассмотреть взаимодействие движущегося электрического заряда q с электрическим полем Е'0 (95) от покоящихся зарядов, то с учетом запаздывающих потенциалов и деформации электрического поля Е движущегося заряда это взаимодействие будет отражено зависимостью
Принимая во внимание массу m заряда и приобретаемое массой ускорение w, этой же зависимости можно придать вид
Зависимость (101) отражает собой релятивистский эффект уменьшения силы взаимодействия движущегося заряда с электрическим полем Е0 покоящихся зарядов. В рамках же релятивистских представлений современной электродинамики зависимость (101) интерпретируется как эффект "увеличения массы" m0 движущегося заряда, если радикал из левой части перенести направо:
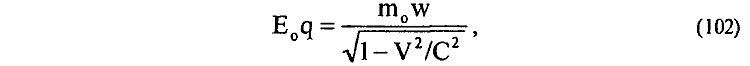
априорно полагая при этом, что электрическое поле движущегося заряда и сам электрический заряд не претерпевают каких-либо деформаций. Следовательно, и в данном случае известные спорные релятивистские представления об "увеличении массы" m0 движущегося заряда до бесконечности при приближении скорости заряда к скорости света заменяются более приемлемыми, с физической точки зрения, представлениями о деформации электрического поля движущегося заряда и уменьшении до нуля силы взаимодействия с ним внешних полей при приближении скорости заряда к скорости света. Интересны в этом отношении известные механические аналогии взаимодействия вращающегося якоря с вращающимся магнитным полем статора в синхронном электродвигателе. По мере приближения скорости вращения якоря к скорости вращения магнитного поля статора сила вращающего момента, приложенная к якорю, уменьшается, приближаясь к нулевому значению. Данная механическая аналогия, конечно, далека от действительной физики взаимодействия движущегося заряда с электрическим полем, но в ней заложен достаточно глубокий физический смысл этого взаимодействия.
Таковы в общих чертах перспективы построения более или менее полностью непротиворечивой электродинамики физического вакуума реального пространства в рамках представления о статических и динамических электрических полях, в которых полностью исключается необходимость оперирования явно формальными представлениями о "магнитных полях" и "магнитных потоках". Однако, к сожалению, в практическом отношении о подобной непротиворечивой электродинамике можно говорить пока только, как о сравнительно далекой желаемой перспективе, ибо, отражая глубоко укоренившиеся и явно ограниченные современные представления об известном в науке векторном магнитном поле HT = rot A, инерция мышления большинства ученых в современной науке настолько велика, что даже частичное совершенствование современной электродинамики дополнением ее заведомо недостающим скалярным магнитным полем H|| = –div A, легко устраняющим многочисленные грубые противоречия как в самой теории, так и в экспериментальных наблюдениях, вызывает у специалистов столь резкую отрицательную реакцию, что можно усомниться в их искреннем стремлении избавиться от имеющихся в современной электродинамике противоречий и парадоксов. При этом некоторые специалисты откровенно отрицают необходимость каких-либо изменений укоренившихся в электродинамике представлений. Другие проявляют явное непонимание внутренней противоречивости и парадоксальности современных методов в электродинамике и отрицают существование в ней даже известных трудностей и противоречий. Что же касается обнаруживаемых парадоксальных, с позиций современных представлений, экспериментальных результатов, то специалисты либо предпринимают безуспешные попытки объяснить их в рамках известных и противоречивых лоренцевских магнитных сил взаимодействия, либо только "авторитетно" ссылаются на возможность найти такое объяснение, даже не пытаясь найти его. Однако в большинстве специалисты обходят почему-то молчанием результаты экспериментальных наблюдений, отдавая предпочтение обсуждению теоретических вопросов, не выходя при этом за рамки известного.
|
|
 |
