Николаев Г. В.
1. В научной литературе, в общем, известно, что третий закон механики в электродинамике нарушается. Однако, к сожалению, не все авторы пособий по электродинамике и монографий как в прошлом, так и в настоящем считали необходимым упоминать об этом малоприятном факте, так как в этом вопросе много неясного и противоречивого. Если же авторы не могут дать каких-либо новых пояснений по этому вопросу, то находят лучшим вообще не упоминать о нем. В результате же знакомства с такими источниками по электродинамике может действительно создаться впечатление, что никаких нарушений третьего закона механики в электродинамике вообще нет. И именно такие утверждения как раз и проскальзывают у некоторых рецензентов. Однако те же рецензенты, которые знакомы, в какой-то степени, с данной противоречивой ситуацией в электродинамике, ссылаются в основном на книгу И. Е. Тамма [13], в которой изложены некоторые пояснения к этому парадоксу. В книге И. Е. Тамма, в частности, говорится: "В случае постоянных токов, по необходимости являющихся замкнутыми, это нарушение третьей аксиомы Ньютона связано лишь с представлением сил взаимодействия токов как сил попарного взаимодействия их элементов.... Силы же взаимодействия двух замкнутых токов удовлетворяют принципу равенства действия и противодействия". Ссылаясь на столь авторитетное высказывание, не вникая в смысл доказанного, рецензенты полагают, что вопрос о взаимодействии токов является уже окончательно решенным и не подлежащим дальнейшей дискуссии. Конечно, авторитет автора книги достаточно большой, и если интересы познания действительной физической сущности явления не ставить на первое место, то таким авторитетом можно легко прикрыться как непроницаемым щитом, что в действительности иногда имело место. В чем же физический смысл приводимых в книге И. Е. Тамма доказательств и можно ли считать, что эти доказательства действительно устраняют известную в электродинамике парадоксальную ситуацию с нарушением третьего закона механики? Прежде всего, следует обратить внимание на тот факт, что в книге И. Е. Тамма, в общем, не отрицается существование в электродинамике серьезных противоречий с третьим законом механики для случая "попарного" взаимодействия отдельных элементов тока. И, в частности, шестью строками выше взятой из книги И. Е. Тамма ссылки прямо указывается, что "особенно же резко проявляется нарушение принципа равенства действия и противодействия (подчеркнуто в книге!) в том случае, если, например, dS1 параллельно R12, а dS2 перпендикулярно R12 (случай перпендикулярных элементов тока). В этом случае |dS1xR12| = 0, и поэтому F12 = 0, тогда как |dS2xR12| <> 0 и F21 <> 0; элемент dS1 (тока) испытывает силу со стороны элемента dS2 (тока), но сам на него не действует". Следующие же за этим выводы автора книги относительно случая "постоянных токов, по необходимости являющихся замкнутыми...", на которые решили сослаться рецензенты, отражают собой лишь попытку автора книги уйти от явных (и не отвергаемых им же) противоречий с третьим законом механики в электродинамике, но уже для случая замкнутых токов, причем не без помощи, в общем, формальных математических допущений и априорных заключений. Следовательно, в книге И. Е. Тамма нет никаких доказательств, что парадоксальная ситуация с нарушением третьего закона механики в электродинамике для случая элементов тока разрешена и не является актуальной.
Что же касается приводимых в книге доказательств о возможности уйти от этой парадоксальной ситуации, если рассмотреть взаимодействие замкнутых контуров, то предметом обсуждения как раз и должны стать примененные при доказательствах формально-математические методы и априорные допущения. Для большей достоверности обратимся к конкретному примеру.
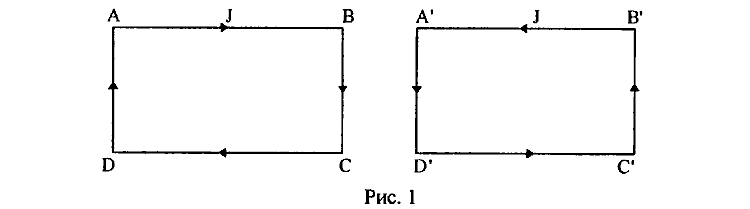
Рассмотрим простейший пример магнитного взаимодействия двух расположенных в одной плоскости прямоугольных контуров АВСД и А'В'С'Д' (рис. 1).

Чтобы определить действие "магнитного поля" одного контура АВСД на ток другого контура А'В'С'Д', необходимо найти суммарное магнитное поле Н0 контура АВСД в точках вдоль сторон другого контура А'В'С'Д' с током, однако это определение возможно осуществить с помощью известной интегральной зависимости
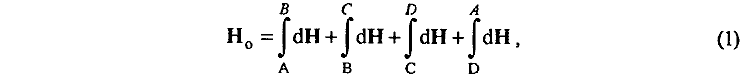
отражающей физический принцип суперпозиции. Согласно этому принципу, игнорирование которого недопустимо для специалиста, суммарное действие всего "магнитного поля" Н0 контура АВСД на токи в сторонах А'В', В'С', С'Д', Д'А' контура А'В'С'Д'
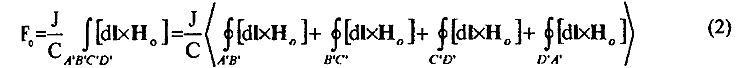
складывается из действия магнитных полей токов каждой стороны контура АВСД на токи в сторонах А'В', В'С, С'Д', Д'А' контура А'В'СД', т. е.
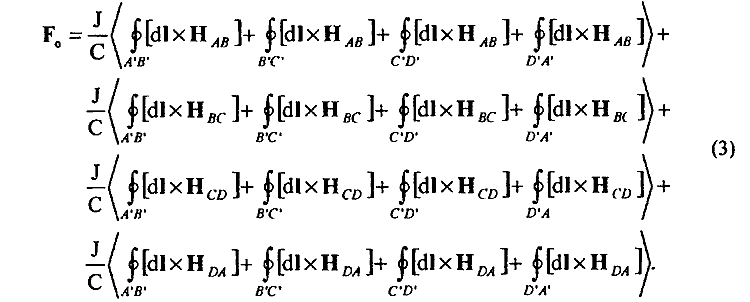
Более того, в реальном случае при определении суммарной силы F0 (3) в конкретной практической задаче приходится определять именно эти многочисленные интегралы, отражающие не что иное, как попарное магнитное взаимодействие сторон контуров, так как другого способа определения воздействия всего "магнитного поля" контура АВСД на токи в сторонах контура А'В'С'Д' в физике просто неизвестно. Таким образом, зависимость (3) отражает действие всего "магнитного поля" Н0 контура АВСД на токи другого контура, однако анализ этой зависимости в рамках известных представлений о взаимодействии тока с магнитным полем сразу же обнаруживает странности. Во-первых, члены 1 и 11 справа вообще равны нулю. Кроме того, попарные члены 3 и 9, 5 и 7, 13 и 15 также дают равную нулю суммарную силу взаимодействия. Так что сила взаимодействия F (3) между замкнутыми контурами будет определяться всего только 8-ю членами зависимости (3), т. е.
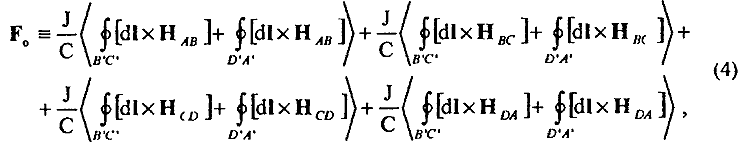
другими словами, действием магнитных полей НАВ, НВС, НСД, НДА всех четырех сторон контура АВСД (или действием всего "магнитного поля" Н0 контура) только на две стороны В'С' и Д'А' замкнутого контура А'В' С'Д'. Уже на этом этапе, причем в рамках общепринятых представлений, обнаруживается парадоксальная ситуация, заключающаяся в том, что действие всего "магнитного поля" Н одного контура распространяется почему-то не на все проводники с током другого контура, а только на два проводника В'С' и Д'А'. Так как результирующее действие на токи двух других сторон А'В' и С'Д' контура А'В'С'Д' равно нулю, то вполне очевидно, что суммарная сила F0 (4) магнитного действия не изменит своего значения, если токи в сторонах А'В' и С'Д' вообще будут исключены из рассмотрения. Например, если токи в сторонах В'С', Д'А' представить в виде движущихся заряженных проводников (или пучков заряженных частиц), то действие на эти токи (пучки) со стороны всего "магнитного поля" Н0 замкнутого контура АВСД как раз и определится зависимостью (4) в полном соответствии с известными представлениями о законах магнитного взаимодействия. Однако если при этом попытаться решить обратную задачу и в рамках тех же известных представлений определить теперь суммарное "магнитное поле" Н' двух отрезков тока в сторонах В'С', Д'А' и определить действие этого "магнитного поля" Н0' на токи контура АВСД, то сразу же обнаруживаем, что суммарное действие F0' определится теперь только четырьмя не равными нулю членами:

и что по величине эта сила F0' (5) уже не соответствует силе F0' (4). Вновь налицо грубое нарушение третьего закона механики, причем для случая взаимодействия всего "магнитного поля" контура с постоянным током с помещенными в его поле отрезками другого тока. Возникает вопрос, чем вызвано появление этого противоречия? Если вновь вернуться к выражению (4), то можно обнаружить, что на отрезок тока А'Д' контура А'В'С'Д', например, действуют магнитные поля от всех четырёх сторон контура АВСД и создают при этом силу взаимодействия, направленную по прямой, соединяющей рассматриваемые контуры. Если же вспомнить законы механики, то мы должны, очевидно, ожидать, что на все четыре стороны контура АВСД должна быть распределена равная и противоположно направленная реакция со стороны магнитного поля отрезка тока А'Д' контура А'В'С'Д'. Однако если получить аналогичное (4) выражение для силы взаимодействия магнитных полей сторон контура А'В'С'Д' со сторонами контура АВСД, то неожиданно устанавливаем, что сторона А'Д' своим магнитным полем создает реакцию вдоль направления прямой, соединяющей рассматриваемые контура, только на две стороны ВС и ДА контура АВСД, а не на все 4 стороны, как этого следовало бы ожидать в согласии с законами механики. В частности обнаруживается, что сторона А'Д' своим магнитным полем на токи в сторонах АВ и СД контура АВСД вообще не действует вдоль прямой, соединяющей данные контура. То есть не создает той реакции, которая должна быть с учетом выполнимости законов механики. Следовательно, если допустить, что законы механики должны выполняться, то на стороны АВ и СД контура АВСД должны действовать еще 4 дополнительные силы реакции от сторон А'Д' и В'С' контура А'В'С'Д', которые в выражении (4) просто не отражены из-за ограниченности используемых представлений о законах магнитного взаимодействия. В свою очередь, если учитывать дополнительные силы реакции полностью, то каждый из попарных членов 5 и 7, 13 и 15 в выражении (4) окажется уже не равным нулю. При этом все стороны контура А'В'С'Д' (а не две стороны А'Д' и В'С') будут подвержены уже действию со стороны всех же сторон контура АВСД без каких-либо противоречий.
Таким образом, равный нулю вклад членов 5, 7, 13, 15 в выражении (4) как раз и обусловлен ограниченностью используемых общепринятых представлений о законе магнитного взаимодействия. В результате проведенного анализа становится также понятным, что удовлетворение третьему закону механики в магнитном взаимодействии одного замкнутого контура с другим, в рамках известных представлений, обусловлено всего лишь тем, что при рассмотрении действия одного контура на другой полностью игнорируется продольная реакция на его боковые стороны со стороны другого контура, существование которой является необходимым при условии выполнимости третьего закона механики. И, наоборот, при рассмотрении действия второго контура на первый, опять же, полностью игнорируется продольная реакция уже на его боковые стороны со стороны первого контура. Так как в противодействии и действии сторон контуров игнорируется существование равных по величине и одинаковых по природе продольных магнитных сил реакций, то равенство действия и противодействия во взаимодействии замкнутых контуров, в общем, соблюдается, но при несколько заниженной общей силе взаимодействия между ними. Между тем как с учетом выполнимости третьего закона механики в магнитном взаимодействии сторон контуров выполнимость условия равенства действия и противодействия будет просто естественным условием, но только при несколько увеличенной суммарной силе взаимодействия между рассматриваемыми замкнутыми контурами. Следовательно, можно уже однозначно утверждать, что в рамках известных представлений удовлетворение третьему закону механики в магнитном взаимодействии замкнутых контуров достигнуто за счет грубого искажения действительной физической сущности явления и, более того, некоторого изменения ее величины.
Следует отметить, что из самого факта возможности грубого нарушения третьего закона механики в магнитном взаимодействии перпендикулярных элементов тока непосредственно следует, что в силу выполнимости принципа суперпозиции такое же грубое нарушение третьего закона механики следует ожидать и в магнитном взаимодействии, опять же, перпендикулярных, но уже макроскопических отрезков тока, составляющих, например, реальный замкнутый контур, что в действительности и имеет место. Ну а если же это так, то принципиальный подход к вопросу устранения любых противоречий с третьим законом механики в электродинамике должен основываться, прежде всего, на устранении этих противоречий в исходных предпосылках этой теории, допускающих возможность таких нарушений в магнитном взаимодействии попарных элементов тока.
2. Отстаивая возможность устранения нарушения третьего закона механики в электродинамике переходом к замкнутым токам, как это показано в книге И. Е. Тамма, рецензенты никогда не упоминают о том, что формализм математических доказательств этого перехода основан на переходе от лоренцовской функции взаимодействия между сторонами контуров к потенциальной функции взаимодействия, из которой явно следует возможность существования отрицаемого рецензентами явления продольного магнитного взаимодействия. Прикрываясь авторитетом книги в тех случаях, когда поднимается вопрос о нарушениях законов механики в электродинамике, рецензенты стараются просто обходить молчанием достаточно корректные, но формальные по существу выводы автора книги в том случае, когда поднимается вопрос о существовании продольных магнитных сил, направленных вдоль тока. Голословно отрицая возможность существования продольных сил магнитного взаимодействия, рецензенты почему-то стараются уже не ссылаться на авторитет книги И. Е. Тамма, а сетуют уже на отсутствие в физике экспериментальных доказательств этого явления. А между тем, если быть последовательным, рецензентам следовало бы, прежде всего, дать разъяснение выводам И. Е. Тамма, из которых следует явно не лоренцевский закон взаимодействия между элементами dl1, и dl2 замкнутых контуров:
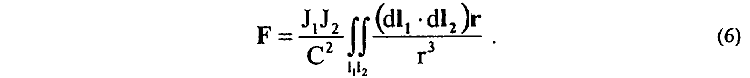
Аналогичные записи для сил взаимодействия элементов тока используются и в других работах [83]. Для полного представления о существе зависимости (6) проведем анализ представленного в книге И. Е. Тамма (стр. 228) перехода от непотенциальной функции взаимодействия к потенциальной.
Рассмотрим взаимодействие замкнутого контура АВСДКМ с током J1 с магнитным полем Н2 от элемента dl2 тока J2 (рис. 2).
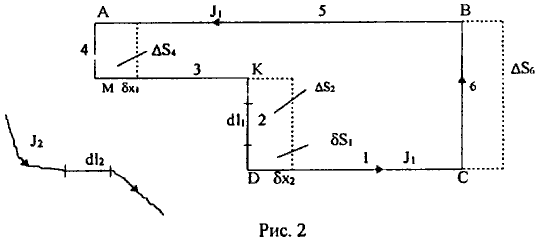
Линейный элемент dl2 тока J2 выбран таким образом, что он расположен на одной прямой со стороной СД замкнутого контура и параллелен сторонам АВ и КМ. В магнитном поле Н2 элемента dl2 тока J2 на любой элемент dl1 тока J1 замкнутого контура будет действовать сила Лоренца
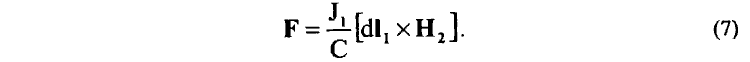
Определим работу, совершаемую замкнутым контуром с неизменным током J1 в магнитном поле Н2 при его виртуальном перемещении δx вдоль стороны ДС. В этом случае для работы перемещения любого элемента dl1 контура можно, очевидно, записать
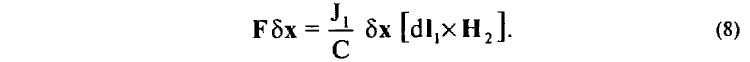
Общая же работа δA, связанная с перемещением всех элементов контура L с током J1, будет равна
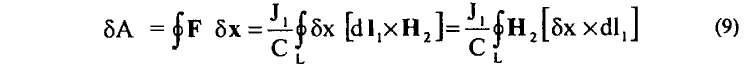
где | δx x dl1 | = δS1 — есть элемент площади, описанной элементом dl1 при его виртуальном перемещении δx.
С учетом (9) для работы 6А можно еще записать
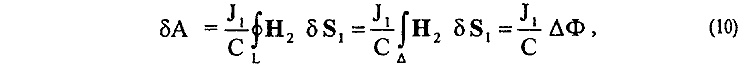
то есть интегрирование можно проводить уже только по сторонам ДК, МА, ВС, так как другие стороны магнитного потока δФ от магнитного поля Н2, по условию, не пересекают. Записи (10) можно придать еще вид
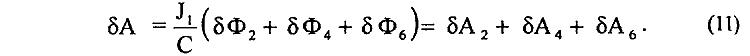
Из рис. 2 видно, что магнитные потоки Ф2 , Ф4 , Ф6 локализуются, в основном, около тех сторон контура, перемещением которых совершается работа δА2, δА4, δА6, причем вклад в работу δА каждой из этих сторон определяется величиной силы (7), действующей на элемент dl1 этих сторон и направленной вдоль направления перемещения δx. Следовательно, напрашивается вывод, что магнитное взаимодействие замкнутого контура АВСДКМ с магнитным полем Н2 элемента dl2 тока J2 обусловлено, в основном, взаимодействием его сторон ДК, МА, ВС, перемещением которых как раз и совершается работа δA (9). Однако можно показать, что равенство (10) для работы δA, т.е. выражение
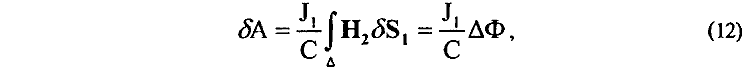
количественно не изменится, если допустить, что поток δФ изменяется не около сторон ДК, МА, ВС, а внутри всего замкнутого контура L, охватывающего собой поверхность S, т.е.
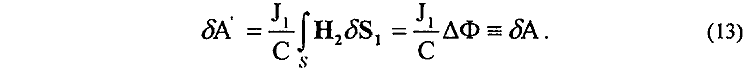
Но в последнем случае, используя теорему Стокса, для (13) можно записать
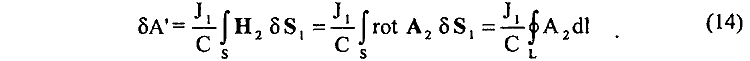
Принимая во внимание, что для векторного потенциала А2 от элемента dl2 тока J2 справедлива запись
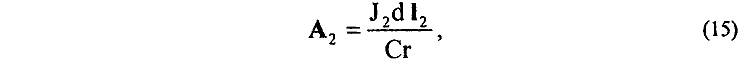
для работы δA' (14) окончательно устанавливаем
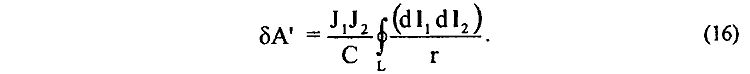
Если учесть, что скалярное произведение под интегралом не равно нулю только для сторон АВ, СД, КМ, то выражение (16) оказывается эквивалентным выражению
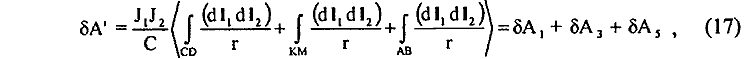
из которого следует, что магнитное взаимодействие замкнутого контура АВСДКМ с магнитным полем Н2 элемента dl2 тока J2 обусловлено, в основном, взаимодействием уже сторон СД, КМ, АВ этого контура с векторным потенциалом А2 элемента dl2 . Причем во взаимодействии с элементом dl2 тока J2 участвует даже сторона СД замкнутого контура, лежащая на одной прямой с элементом dl2, между тем как обычное лоренцевское взаимодействие между ними вообще исключается. Из анализа (9) и (13) можно сделать уже вывод, что допущение (13), в общем, является, с математической точки зрения, достаточно корректным, однако с физической точки зрения переход от (9) к (13) нельзя считать корректным, так как он приводит к существенному изменению физической сущности рассматриваемого явления. Формальный характер сделанных в (13) допущений заключается в том, что действующие на стороны замкнутого контура АВСДКМ действительные магнитные силы Лоренца F (7) оказались распределенными по сторонам контура уже по другому закону. Так как изменение потока δФ (10) в замкнутом контуре L стало безотносительным к сторонам этого контура, то закон Лоренца попарного взаимодействия элемента dl2 тока J2 с элементами dl1 тока J1 замкнутого контура, противоречащий третьему закону механики, заменяется уже не противоречащим третьему закону механики потенциальным взаимодействием этих же элементов в другой их комбинации. Однако никакого реального физического смысла подобная замена не имеет. Например, если такую же замену осуществить для двух взаимодействующих контуров (см. выше п/п 1 этой части), то можно заметить, что если первоначально магнитное взаимодействие между контурами было обусловлено частично потенциальной частью лоренцевского взаимодействия (первый член справа):
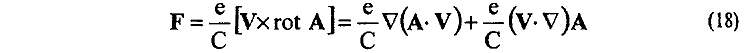
и неполностью непотенциальной частью (не учитывается реакция во взаимодействии перпендикулярных сторон контуров), то после замены взаимодействие оказывается обусловленным уже полностью потенциальной частью взаимодействия, но зато при полном отсутствии непотенциального взаимодействия между перпендикулярными сторонами контуров. Как в первом, так и во втором случаях физика взаимодействия между замкнутыми контурами отражается неполностью.
3. Большое внимание в дискуссиях с рецензентами занимала
проблема, связанная с явлением движения П-образного проводника, и
проблема так называемых "рельсотронных двигателей". Сущность проблемы,
которая была описана еще Ампером [27], заключается в том, что одними
поперечными лоренцевскими силами корректного объяснения явлению найти не
удается. Несмотря на то, что парадоксальность ситуации с П-образным
проводником в электродинамике остается, в общем, давно известной, в
дискуссиях рецензенты предпринимают усиленные попытки дать этому явлению
непротиворечивое объяснение, причем в рамках известных представлений. В
своих доводах рецензенты, в частности, утверждают, что "задача
определения воздействия токов разбивается на две...: а) определение
магнитного поля произвольного тока и б) определение сил, действующих в
заданном магнитном поле на помещенный в него ток". 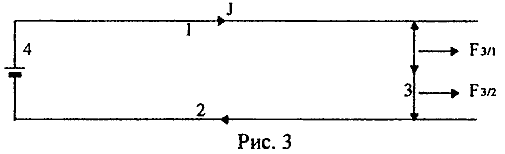 На основании этих общих рассуждений о действии всего "магнитного поля" на токи делается вывод, что "никакого
нарушения третьего закона механики для постоянных токов нет, в том
числе и для устройств так называемого "рельсотронного типа". Для того чтобы разобраться в существе парадоксальной ситуации, рассмотрим ряд конкретных примеров.
На основании этих общих рассуждений о действии всего "магнитного поля" на токи делается вывод, что "никакого
нарушения третьего закона механики для постоянных токов нет, в том
числе и для устройств так называемого "рельсотронного типа". Для того чтобы разобраться в существе парадоксальной ситуации, рассмотрим ряд конкретных примеров.
Рассмотрим явление движения прямолинейного проводника 3 в электродинамическом двигателе "рельсотронного типа" (рис. 3).
Для достоверности будем оперировать конкретными числами, что длина стороны АВ (1,2) равна L = 300 см, а длина стороны ВС (3,4) равна l = 30 см. В замкнутой цепи создается электрический ток величиной J = 400 А. Поперечная сила Лоренца FT магнитного давления на проводник 3 определяется вычислениями в рамках известных представлений:
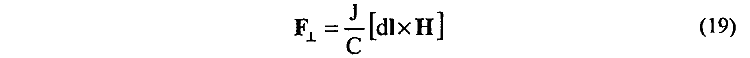
и измеряется динамометром. Для определения суммарной силы F3, действующей на проводник 3, определим сначала, согласно общепринятым правилам, действие магнитных полей Н1, Н2, Н4 проводников 1, 2, 4 на элемент тока J dl3 проводника 3
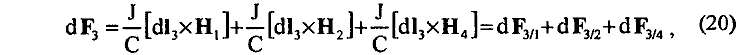
где Н1, Н2 , Н4 — суммарные магнитные поля отдельно от тока J в проводниках 1, 2, 4 в точке нахождения элемента dl3 проводника 3.
Однако если в противоположность известным в электродинамике представлениям в выражение (20) дописать еще один член
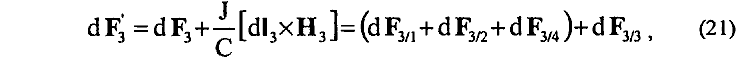
учитывающий взаимодействие элемента dl3 проводника 3 с собственным магнитным полем Н3 проводника 3, то подобная запись будет находиться, очевидно, в явном противоречии с известными законами механики, так как собственное магнитное поле Н3 проводника 3 не может принимать участия в поступательном перемещении этого же проводника. Следовательно, для суммарной силы F, действующей на весь подвижный проводник 3 со стороны магнитных полей Н1, Н2, Н4 неподвижных проводников, корректная запись должна, очевидно, иметь вид
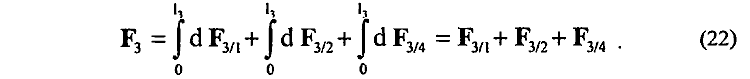
Подставляя в (22) численные величины L = 300см, l =30 см, J = 400 А, для силы F3 устанавливаем
 Ставим эксперимент [39], замеряем силу F3, действующую на проводник 3, динамометром и находим, что она действительно равна F3 = 35 г.
Из соответствия расчетов результатам эксперимента заключаем, что
использованные в расчетах представления о поперечных силах Лоренца FT (19) и суммарной силе F3
(22), действующей на подвижный проводник 3, являются достаточно
верными. С другой стороны, дополнительно убеждаемся в ошибочности
допущения (21). Из сопоставления сил взаимодействия F3/1, F3/2 боковых сторон 1, 2 с подвижным проводником 3 с силой F3/4 взаимодействия удаленного проводника 4 с подвижным проводником 3 находим, что сила F3/4 в 2000 раз меньше сил F3/1 + F3/2.
Ставим эксперимент [39], замеряем силу F3, действующую на проводник 3, динамометром и находим, что она действительно равна F3 = 35 г.
Из соответствия расчетов результатам эксперимента заключаем, что
использованные в расчетах представления о поперечных силах Лоренца FT (19) и суммарной силе F3
(22), действующей на подвижный проводник 3, являются достаточно
верными. С другой стороны, дополнительно убеждаемся в ошибочности
допущения (21). Из сопоставления сил взаимодействия F3/1, F3/2 боковых сторон 1, 2 с подвижным проводником 3 с силой F3/4 взаимодействия удаленного проводника 4 с подвижным проводником 3 находим, что сила F3/4 в 2000 раз меньше сил F3/1 + F3/2.
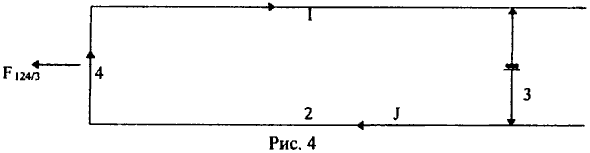
Обращаем эксперимент, оставляя проводник 3 в покое, а П-образному проводнику (из проводников 1, 2, 4) предоставляем возможность двигаться в обратную сторону (рис. 4).
Используя физические представления, заложенные в (22), для силы dF124, действующей на элементы dl1, dl2, dl4 подвижных проводников 1, 2, 4 с током J со стороны магнитного поля Н3 неподвижного проводника 3, находим

Откуда для суммарной силы F124 , действующей на проводники 1, 2, 4 П-образной рамки, получаем
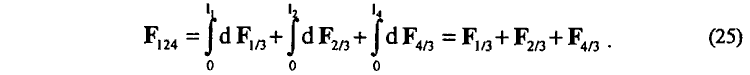
Так как силы F1/3 и F2/3
перпендикулярны к проводникам 1 и 2 и компенсируются наличием жесткой
связи между этими проводниками, то для (25) окончательно находим
Подставляя в (26) численные величины L = 300 см, l = 30 см, J = 400 А, для результирующей силы F124, действующей на П-образный проводник, устанавливаем
Ставим эксперимент [39] и замеряем силу F124, приложенную к П-образному проводнику 1, 2, 4 и в результате измерения устанавливаем, что эта сила равна F = 35 г. Из несоответствия расчетов результатам эксперимента заключаем, что использованные в расчетах представления об одних поперечных силах Лоренца (19), действующих на подвижный П-образный проводник, являются недостаточными. Дополнительно можно отметить, что в рамках известных представлений об одном векторном магнитном поле и явлении поперечного магнитного взаимодействия обнаруживаемое противоречие является принципиально неразрешимым. И тем не менее, несмотря на явную ограниченность известных представлений, попытки обойти трудности в электродинамике окольными путями продолжаются. Нетрудно показать, что если в описываемом выше эксперименте допустить невозможное, с точки зрения законов механики, и предположить, что на сторону 4 П-образного проводника оказывают давление еще магнитные поля и от жестко связанных с ним боковых проводников 1, 2, то суммарная сила F'124, действующая на П-образный проводник, оказывается равной F'124 = 35 г, что как раз и наблюдается в эксперименте. Именно к подобной интерпретации результатов эксперимента вынужден был прийти сам автор этого эксперимента [39], так как другого выхода из противоречия найти не мог. К сожалению, подобную же интерпретацию результатов эксперимента с П-образным проводником пытались защищать и некоторые из рецензентов, грубо игнорируя известные положения механики, что внутренние силы между проводниками П-образной рамки не могут быть причиной поступательного движения этой рамки.
4. Другая группа рецензентов в попытках уйти от противоречий в экспериментах с П-образным проводником и "рельсотронными" двигателями ссылается на применимость к этим явлениям известной потенциальной зависимости для энергии контура
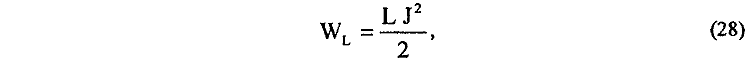
из которой действительно можно найти как силу, действующую на подвижный проводник 3 (см. рис. 3)
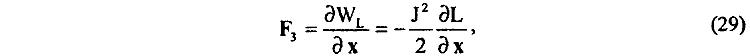
так и равную и противоположно направленную
силу реакции, действующую на неподвижный П-образный проводник.
Исследования показывают, что величины этих сил действительно
соответствуют реально наблюдаемым в эксперименте силам. Однако
применительно к подвижному проводнику 3 "рельсотронного" двигателя
зависимость (29) не позволяет получить непротиворечивый ответ
относительно конкретного места приложения сил реакции от подвижного
проводника. Вопрос о месте приложения сил реакции приобретает в
настоящее время актуальное значение в связи с тем, что в "рельсотронных"
пушках силы реакции оказываются уже соизмеримыми с предельно
допустимыми для конструкции силами. 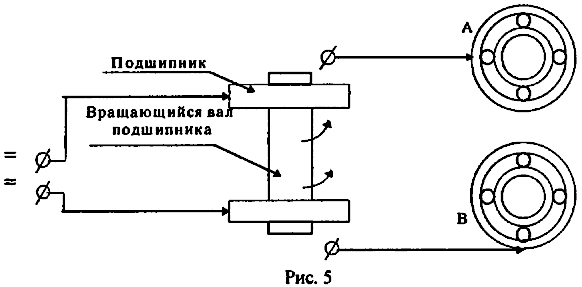 Кроме
того, в случае неподвижных частей контура из зависимости (29) вообще
невозможно определить известные действующие в контуре статические
магнитные силы. Главное же возражение против использования зависимости
(29) заключается в том, что эта зависимость вообще не затрагивает собой
проблемы парадокса с "рельсотронными" двигателями и, более того,
находится в явном противоречии с действующими в контуре известными
лоренцевскими силами. Особенно наглядно ограниченность зависимости (29)
обнаруживается применительно к "рельсотронным" двигателям, у которых
размер рабочего контура не изменяется (см. эксперименты 43, 44 3-й части
обзора). Один из таких оригинальных экспериментов был осуществлен на
кафедре электрических машин ТПУ (г. Томск), когда через ось, находящуюся
на двух подшипниках, пропустили электрический ток (постоянный или
переменный), подведя его к внешним кольцам подшипников (рис. 5).
Кроме
того, в случае неподвижных частей контура из зависимости (29) вообще
невозможно определить известные действующие в контуре статические
магнитные силы. Главное же возражение против использования зависимости
(29) заключается в том, что эта зависимость вообще не затрагивает собой
проблемы парадокса с "рельсотронными" двигателями и, более того,
находится в явном противоречии с действующими в контуре известными
лоренцевскими силами. Особенно наглядно ограниченность зависимости (29)
обнаруживается применительно к "рельсотронным" двигателям, у которых
размер рабочего контура не изменяется (см. эксперименты 43, 44 3-й части
обзора). Один из таких оригинальных экспериментов был осуществлен на
кафедре электрических машин ТПУ (г. Томск), когда через ось, находящуюся
на двух подшипниках, пропустили электрический ток (постоянный или
переменный), подведя его к внешним кольцам подшипников (рис. 5).
В случае симметричного подвода тока (рис. 5, А) ось "двигателя" начинает раскручиваться в любую сторону после первого толчка. При асимметричном (рис. 5, В) — "двигатель" начинает работать без предварительной раскрутки. В данном реально наблюдаемом в эксперименте явлении при постоянной угловой скорости вращения оси на подшипниках размеры контура, а следовательно и его индуктивность L, не изменяются, и зависимость (29) оказывается в принципе неприменимой. Анализ работы устройств такого типа показывает, что движущими силами в них являются непотенциальные поперечные силы Лоренца, приложенные к радиальным токам вращающегося якоря, между тем как продольные силы реакции приложены к токам в токоподводящих "рельсах".
5. При взаимодействии перпендикулярных элементов тока поперечная сила Лоренца FT от известного магнитного поля НT, действующая на один элемент, компенсируется равной и противоположно направленной продольной силой реакции от другого типа магнитного поля Н||, приложенной ко второму элементу, разрешая известный в электродинамике парадокс с третьим законом механики. Возражая против подобной интерпретации и отвергая возможность существования второго типа магнитного поля, некоторые из рецензентов утверждают, что "в положениях автора принцип равенства действия и противодействия в действительности не выполняется, поскольку направления сил, приложенных к двум элементам тока, не находятся на одной прямой". Следует отметить, что постановка вопроса о справедливости принципа равенства действия и противодействия в таком виде не совсем корректна. Как известно из литературы [84], сущность третьего закона механики Ньютона основывается на двух основополагающих утверждениях, фундаментальность которых различна. Первое утверждение, фундаментальное значение которого является определяющим, гласит, что для двух взаимодействующих частиц (тел) силы, действующие на них, равны по величине и противоположны по направлению. Данное утверждение определяет фундаментальную сущность третьего закона механики и применимо для всех видов взаимодействий как потенциальных, так и непотенциальных. Условие выполнимости первого утверждения третьего закона механики Ньютона математически записывается в виде
Второе утверждение, справедливость которого ограничивается механическими взаимодействиями и взаимодействиями через потенциальные силовые поля, гласит, что сила действия и сила противодействия находятся на одной прямой. Условие выполнимости второго утверждения третьего закона механики Ньютона математически записывается в виде
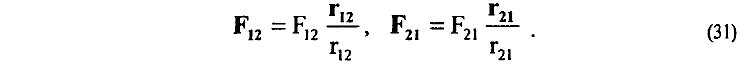
Как известно из литературы, силовое поле Е (или Н и т.д.) называется потенциальным, если для этого поля выполняется условие
В свою очередь, сила взаимодействия частиц в потенциальных полях называется потенциальной силой и определяется выражением

Для двух взаимодействующих частиц в потенциальных полях оказываются справедливыми оба утверждения третьего закона механики (30), (31). Взаимодействия частиц, подчиняющиеся (30) и (31), называются центральными взаимодействиями, а силы — центральными силами.
Однако, кроме потенциальных полей, в природе существуют еще поля непотенциального типа, например поля А, НT, Е и т. д., для которых условие (31) явно невыполнимо, так как невыполнимо условие (32). Например, в случае одиночного движущегося с ускорением заряда для полей НT и Е имеем
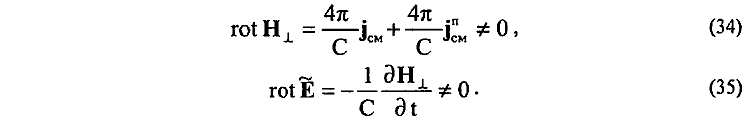
Для полей непотенциального типа (34), (35), а также при наличии у
частиц внутренних векторных характеристик (дипольных моментов, спинов и
т. д.) и в случае релятивистских скоростей [84] "первое утверждение F12 = –F21 , содержащееся в третьем законе механики (30), сохраняет силу, однако второе утверждение ![]() — оказывается несправедливым. Это означает, что силы взаимодействия
между частицами в этих случаях перестают быть центральными
(направленными по прямой, соединяющей частицы)".
— оказывается несправедливым. Это означает, что силы взаимодействия
между частицами в этих случаях перестают быть центральными
(направленными по прямой, соединяющей частицы)".
Таким образом, фундаментальный принцип третьего закона механики — принцип равенства и противоположной направленности действия и противодействия (30) — должен оставаться справедливым для любых известных в природе видов взаимодействий, между тем как, в рамках известных представлений, в электродинамике имеют место грубые нарушения этого принципа как в магнитных взаимодействиях элементарных зарядов и элементов тока в контуре, так и в магнитных взаимодействиях токов с замкнутыми контурами и замкнутых контуров между собой. Кроме того, в рамках известных представлений, при выполнимости условия (30) и невыполнимости (31), делать выводы о невыполнимости в целом третьего закона механики недопустимо.
 Для
наглядного представления о физической сущности непотенциальных полей,
нарушающих условие (31), рассмотрим для примера, взаимодействие
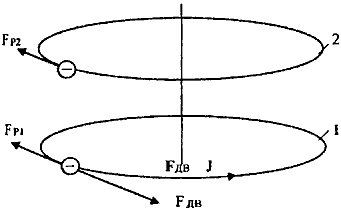
непотенциального вихревого электрического поля A (35) ускоренно движущихся зарядов замкнутого кругового контура 1 с зарядами аналогичного же кругового контура 2 (рис. 6).
Для
наглядного представления о физической сущности непотенциальных полей,
нарушающих условие (31), рассмотрим для примера, взаимодействие
непотенциального вихревого электрического поля A (35) ускоренно движущихся зарядов замкнутого кругового контура 1 с зарядами аналогичного же кругового контура 2 (рис. 6).
Приложение ускоряющей силы FДВ к зарядам одного контура 1 вызывает индукцию вихревого электрического поля A , которое создает силы реакции FР1 и FР2 на зарядах контура 1 и 2. Причем сила реакции FР2, приложенная к зарядам второго контура 2, не находится на одной прямой с силой ускорения FДВ, приложенной к зарядам первого контура 1. Однако суммарная сила реакции (FР1 + FР2) равна и противоположно направлена ускоряющей силе FДВ.
6. Рассмотрим еще одно противоречивое следствие известных формальных методов электродинамики, используемых в книге И. Е. Тамма (стр. 370, 380) для определения пондеромоторных сил магнитного поля из выражений для энергий
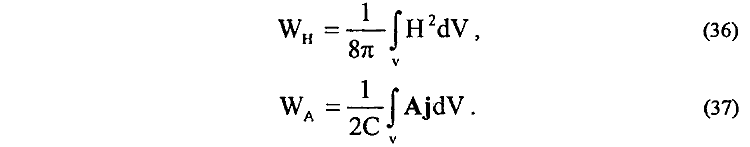
Ссылаясь на доказательства, приведенные в книге, рецензенты ошибочно полагают, что данные выражения для энергии взаимодействия (36), (37) полностью эквивалентны. Выводы их основываются только на приводимых в книге доказательствах без каких-либо попыток их анализа. Сущность же этих доказательств основывается на том, что из зависимости (37) для полной энергии взаимодействия
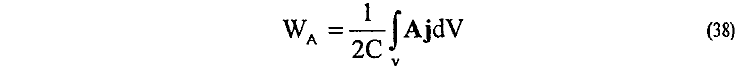
подстановкой
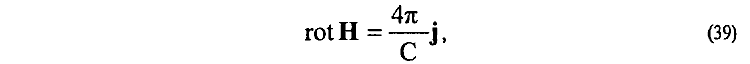
находится
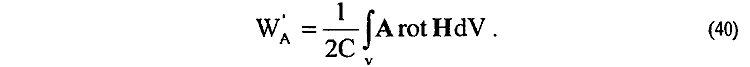
При этом, с учетом
для (40) окончательно устанавливается (в вакууме)
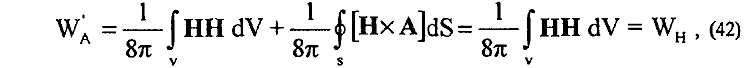
где поверхностный интеграл по бесконечной поверхности полагается равным нулю. В рамках известного в электродинамике формализма, казалось бы, корректным образом устанавливается полная эквивалентность (38) и (42) Однако в действительности соответствия между данными зависимостями не существует. Для того чтобы показать это, выделим из (38) и (42) члены магнитного взаимодействия UА и UH:
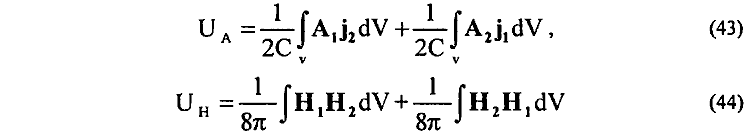
Предположим, что нас интересует энергия взаимодействия двух элементов тока J1dx1 и J2dx2 или элементарных зарядов e1 и e2. В этом случае в (43) интеграл будет равен нулю по всему пространству интегрирования за исключением объемов δV1 и δV2, занимаемых элементами токов J1dx1 и J2dx2:
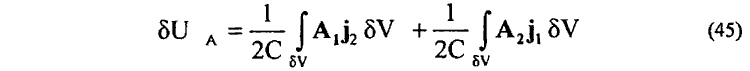
или что то же
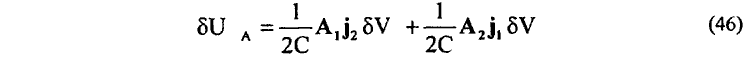
Учитывая
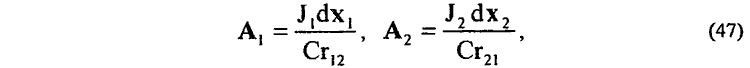
для (46) можно записать
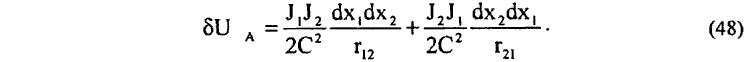
Принимая же во внимание
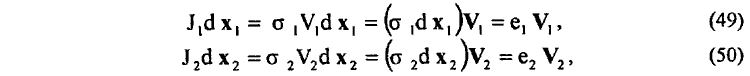
для (48) устанавливаем
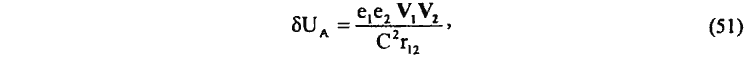
что соответствует полной энергии взаимодействия между двумя движущимися зарядами e1 и e2. Нетрудно теперь показать, что энергия собственного магнитного поля элемента тока J1dx1 будет
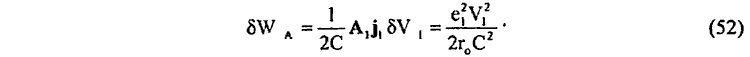
Применительно к энергии магнитного поля электрона, принимая во внимание
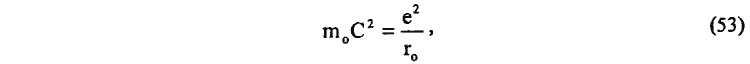
получаем
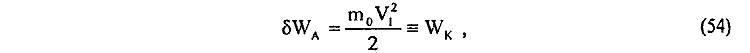
т. е. энергия магнитного поля δWА (54) тождественно равна кинетической энергии электрона. Однако известно [85-87], что для собственной энергии магнитного поля δWН электрона, согласно зависимости (42), имеем
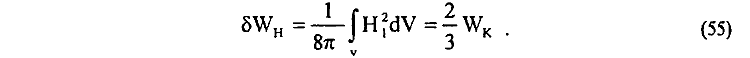
Соответственно и для энергии магнитного взаимодействия δU'А (44) между движущимися зарядами e1 и e2 получаем
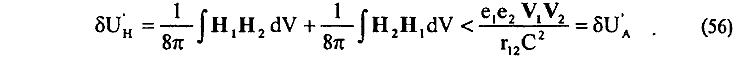
Правильность результата (56) может быть доказана непосредственными
вычислениями, однако интегралы в (56) просто не берутся. Оценить же
значение интегралов (56) можно легко, заменив функцию для магнитного
поля ![]() несколько увеличенной функцией
несколько увеличенной функцией ![]() , т.е. для любой точки интегрируемого пространства положить Н' > Н. В этом случае для левой части (56) будем иметь
, т.е. для любой точки интегрируемого пространства положить Н' > Н. В этом случае для левой части (56) будем иметь
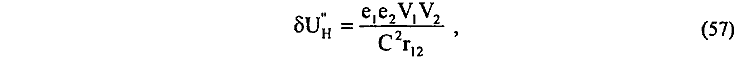
что эквивалентно (51). Из проведенной оценки непосредственно следует, что при условии Н < Н' выражение для энергии δU'А (56) будет иметь заведомо меньшее значение по сравнению с выражением δU"H (57).
Таким образом, выражение для энергии WН (36) действительно не эквивалентно известному выражению для энергии WА (37). Однако возникает вопрос, где же допущена ошибка при, казалось бы, корректном переходе от (38) к (42)? Нетрудно заметить, что важную роль в этом переходе имеет уравнение (39). Выше же во 2-й части обзора уже указывалось на наличие существенной ограниченности данного уравнения в рамках формализма одного магнитного поля. В частности, применительно к незамкнутому току и одиночному движущемуся заряду запись вида (39) уже не представляет собой уравнения, а является просто неравенством. Но в таком случае становится вполне понятным, что если при переходе от (38) к (42) использовано выражение (39), которое является, по существу, неравенством, то выводы об эквивалентности выражений для энергий (38) и (42) нельзя считать корректными.
7. Положительные результаты опытов Аронова-Бома никем уже не оспариваются, однако специалисты отрицают возможность классической интерпретации этих опытов, полагая, согласно устоявшимся представлениям, что это явление только квантовой природы. В связи с этим некоторые из этих специалистов проявляют определенное предвзятое критическое отношение к попыткам интерпретации опытов типа Аронова-Бома эффектом продольного магнитного взаимодействия. Они ошибочно полагают, что в рамках известных представлений из положительных результатов опыта Аронова-Бома вовсе не следует возможность существования продольного силового эффекта и тем более второго типа магнитного поля. А следовательно, эти опыты вообще нельзя считать экспериментальным доказательством существования как явления продольного магнитного взаимодействия, так и второго магнитного поля. Между тем, в противоположность мнению специалистов, можно показать, что, даже не прибегая к помощи каких-либо дополнений и изменений положений электродинамики, то есть находясь в рамках известных представлений, существование явления силового продольного магнитного взаимодействия может быть непосредственно установлено как раз из положительных результатов опыта Аронова-Бома. Выше, в 4-й части обзора, при анализе теоретических противоречий 14, 15 было уже показано, что, не выходя из рамок известных представлений, необходимость существования явления продольного магнитного взаимодействия легко может быть установлена из хорошо известных в электродинамике зависимостей. Ниже будет дано еще несколько вариантов доказательств необходимости существования явления силового продольного магнитного взаимодействия движущегося по оси токового тороида заряда с полем векторного потенциала в опыте Аронова-Бома, причем полученных также в рамках только известных представлений.
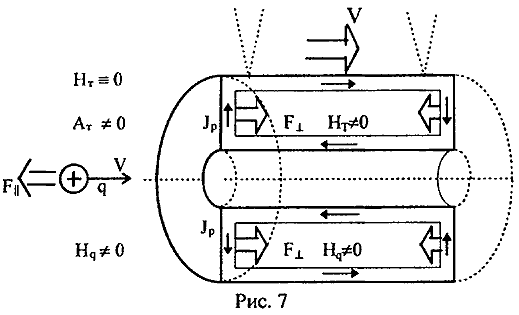 Предположим, что мы имеем подвешенный на тонких нитях идеальный токовый тороид с суммарным осевым током J0 и (для простоты расчетов) без ферромагнитного сердечника (рис. 7). Все магнитное поле тороида HT <> 0,
как известно, сосредоточено внутри него, между тем как вне тороида
существует только не равное нулю поле векторного потенциала AT <> 0. Рассмотрим движущийся со скоростью V по оси тороида в его поле векторного потенциала AT электрический заряд q.
Не выходя из рамок известных представлений, необходимо определить,
какие магнитодинамические силы могут действовать в этом случае на
движущийся электрический заряд.
Предположим, что мы имеем подвешенный на тонких нитях идеальный токовый тороид с суммарным осевым током J0 и (для простоты расчетов) без ферромагнитного сердечника (рис. 7). Все магнитное поле тороида HT <> 0,
как известно, сосредоточено внутри него, между тем как вне тороида
существует только не равное нулю поле векторного потенциала AT <> 0. Рассмотрим движущийся со скоростью V по оси тороида в его поле векторного потенциала AT электрический заряд q.
Не выходя из рамок известных представлений, необходимо определить,
какие магнитодинамические силы могут действовать в этом случае на
движущийся электрический заряд.
1) Из известных представлений о лоренцевском магнитном взаимодействии на движущийся по оси тороида заряд q никаких магнитных сил действовать не должно:
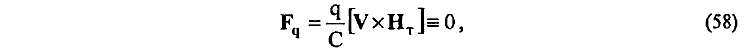
так как вне тороида магнитное поле равно нулю HT = 0. Согласно с (58), принимая во внимание, что токовый тороид с движущимся зарядом не взаимодействует, получим, что и реакция на тороид со стороны движущегося заряда по известным законам механики также должна быть равна нулю. В результате устанавливаем, что тороид не изменит своего состояния покоя на нити подвеса.
Однако, оставаясь в рамках известных представлений, из дальнейших рассуждений находим, что собственное магнитное поле Нq движущегося заряда q во всем окружающем его пространстве, в том числе и внутри тороида, не равно нулю Hq <> 0. Но в таком случае, согласно известным представлениям, на токи тороида будут действовать тривиальные лоренцевские магнитные силы давления
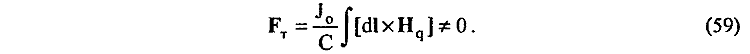
Причем равные и противоположно направленные лоренцевские магнитные силы FT , действующие на осевые токи J0 тороида, будут компенсироваться его жесткой конструкцией, между тем как попарные силы Лоренца FT действующие на радиальные токи JР тороида на его торцах, дают не равную нулю результирующую силу, направленную по его оси. Под действием этой реальной магнитной силы тороид отклонится на подвесе, т. е., согласно известным представлениям, тороид будет испытывать силу магнитного давления от налетающего на него движущегося заряда q. Но тогда становится вполне очевидным, что, согласно известным законам механики, на налетающий на тороид электрический заряд q будет действовать равная и противоположно направленная продольная сила реакции F|| <> 0, которая будет тормозить заряд q, уменьшая скорость его движения.
На первый взгляд, выявленная ситуация, казалось бы, является явно парадоксальной, так как одним известным способом мы устанавливаем, что движущийся заряд q с токовым тороидом взаимодействовать не должен. Между тем как другим известным же способом устанавливаем существование между ними тривиальных магнитных сил взаимодействия. Из двух взаимоисключающих утверждений, полученных при корректном соблюдении известных законов электродинамики, предпочтение следует отдать тому, которое устанавливает существование не нулевого результата, так как в противном случае пришлось бы подвергнуть сомнению корректность известного и хорошо проверенного в электродинамике закона взаимодействия токов с магнитным полем. Нулевой же результат (58) при этом можно отнести, например, к частному случаю либо к случаю, когда не учтены какие-то дополнительные, но, опять же, известные силы.
2) Принимая во внимание, что магнитное поле Нq в пространстве около движущегося заряда q не равно нулю во всем окружающем его пространстве, в том числе и внутри токового тороида, то, согласно известным в электродинамике представлениям, для энергии взаимодействия WH магнитных полей HT и Hq, внутри тороида можно записать (HT <> 0, Hq <> 0)
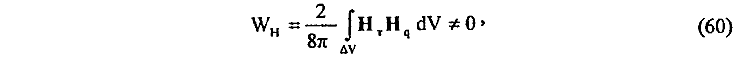
где δV — объем внутренней полости тороида.
Из (60) находим, что энергия взаимодействия WH магнитных полей HT и Hq внутри тороида не равна нулю и является явной функцией от расстояния R между движущимся зарядом q и тороидом, так как магнитное поле Hq, внутри тороида зависит от расстояния R заряда до тороида. Если же это так, то для силы взаимодействия (действия и противодействия) между движущимся зарядом q и токовым тороидом непосредственно устанавливаем
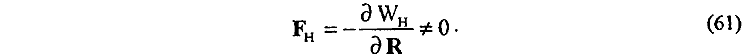
Силе FH (61) можно дать и конкретную физическую интерпретацию. Изменяемый в тороиде дополнительный магнитный поток Фq от магнитного поля Нq движущегося заряда q уменьшает величину суммарного магнитного потока Ф0 в тороиде:
в результате чего в пространстве около тороида индуцируется вихревое электрическое поле индукции A , согласно уже другой известной зависимости:
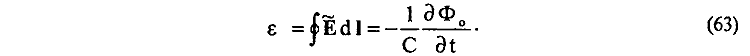
Направление вихревого электрического поля индукции A в пространстве около тороида будет при этом таково, что оно своим действием будет стремиться увеличить ток J0 в тороиде и в то же время тормозить влетающий в тороид электрический заряд q. Следовательно, вновь, без введения каких-либо представлений о новых полях и взаимодействиях, непосредственно устанавливаем, что взаимодействие движущегося заряда q с токовым тороидом не равно нулю.
3) Из известных в электродинамике представлений [13] непосредственно устанавливаем, что энергия взаимодействия WА движущегося заряда q с полем векторного потенциала AT тороида определяется зависимостью
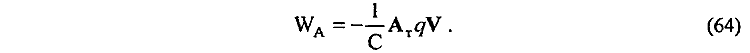
Так как поле векторного потенциала AT в пространстве около тороида не равно нулю AT <> 0 и меняет свою величину при изменении расстояния до тороида, то из выражения WА (64) для силы F||' продольного взаимодействия движущегося заряда q с полем векторного потенциала А непосредственно находим
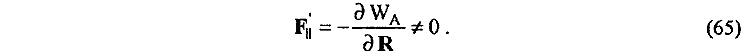
Следует отметить, что из потенциальной зависимости (65) определяется как сила действия на токовый тороид, так и сила противодействия на движущийся заряд. Следовательно, вновь, без каких-либо изменений укоренившихся представлений в электродинамике, между движущимся зарядом и токовым тороидом однозначно устанавливается существование явления продольного магнитного взаимодействия.
Можно показать, что к аналогичному же результату можно прийти в том случае, если рассмотреть полную производную векторного потенциала AT тороида в точке нахождения движущегося со скоростью V заряда q:
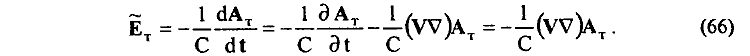
Действие не равного нулю вихревого электрического поля AT (66) на движущийся электрический заряд q в этом случае может быть определено зависимостью
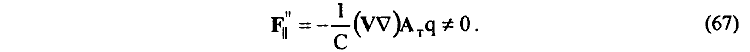
Так как действие силы F||" (67) совпадает с направлением движения заряда q, то сила взаимодействия является продольной.
4) Рассмотрим взаимодействие движущегося заряда q с полем векторного потенциала тороида с позиции принципа относительности. Перейдем в систему отсчета, связанную с движущимся электрическим зарядом q. В этом случае заряд q будет рассматриваться как покоящийся, а токовый тороид, индуцирующий векторный потенциал AT, будет движущимся в направлении к заряду q. Так как векторный потенциал AT тороида в точке нахождения покоящегося заряда q будет изменяться во времени, то это вызовет появление в точке нахождения заряда q вихревого электрического поля A, определяемого известной в электродинамике зависимостью:
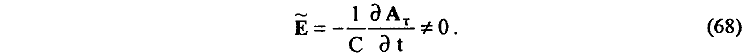
Действие же индуцированного вихревого электрического поля A на покоящийся электрический заряд q, в свою очередь, вызовет появление силы
действующей на заряд q в направлении вдоль оси тороида и вдоль направления его движения.
Таким образом, основываясь на положительных результатах опыта Аронова-Бома и оставаясь в рамках известных представлений, как наглядно показано выше, принципиально разными способами оказывается вполне возможным вновь доказать необходимость существования неизвестного ранее в науке явления продольного магнитного взаимодействия. Откуда следует, что экспериментально обнаруживаемые явления силового эффекта взаимодействия движущихся по оси токового тороида электронов с полем векторного потенциала в опытах типа Аронова-Бома действительно подтверждают собой реальность существования явления продольного магнитного взаимодействия. Ограниченность же проведенных выше доказательств проявляется в том, что все они устанавливают, в общем, разные по величине силовые эффекты взаимодействия. Например, в первом случае рассматривается взаимодействие движущегося заряда q с перпендикулярными радиальными токами тороида JP, но игнорируется взаимодействие этого же заряда с параллельными осевыми токами J0 тороида. Во втором случае рассматривается взаимодействие векторных магнитных полей заряда HTq и тороида HTT, но игнорируется взаимодействие скалярных магнитных полей заряда H||q и тороида H||T. В третьем случае мы имеем обычное потенциальное взаимодействие F||' (65) движущегося заряда q с параллельными токами J0 тороида, при котором полностью исключается взаимодействие с перпендикулярными радиальными токами JP тороида. В четвертом случае сила F||''' (69) не учитывает взаимодействия движущегося заряда q со скалярным магнитным полем Н|| от векторных потенциалов АР1 и АP2 противоположных радиальных токов JP тороида. Дело в том, что сумма векторных потенциалов АР1 и АP2 от радиальных токов на оси тороида равна нулю:
между тем как суммарное скалярное магнитное поле Н||P от этих же векторных потенциалов АР1 и АP2 на оси тороида не равно нулю:
Если принять во внимание суммарное скалярное магнитное поле Н||0 от векторного потенциала А0 осевых токов тороида и суммарное скалярное магнитное поле Н||P от векторных потенциалов АР1 и АP2 радиальных токов тороида, то для полной силы взаимодействия движущегося заряда я с токовым тороидом, в рамках новых представлений, будем иметь
Из сравнения выражений для силы FT (59), F||H, (61), F||' (65), F||'' (69) с суммарной силой F||° (72) обнаруживаем, что все эти выражения дают несколько заниженное по сравнению с F||° значение силы. Из явно же отрицательного результата Fq (58) можно заключить, что известные, укоренившиеся в электродинамике представления о законах магнитного взаимодействия и одних поперечных магнитных силах Лоренца, применительно к описанию конкретного электромагнитного явления реальной действительности, являются заведомо ограниченными.
|
|