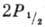 и
и 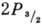 . Возмущающим
фактором является электрич. поле, локализованное в пространстве между зонами
(рис. 1), к-рое резко изменяется на границах, т. е. в пределах каждой
зоны ширины d.
. Возмущающим
фактором является электрич. поле, локализованное в пространстве между зонами
(рис. 1), к-рое резко изменяется на границах, т. е. в пределах каждой
зоны ширины d. Атомный интерферометр - прибор, позволяющий наблюдать стационарную картину интерференции двух сдвинутых по фазе
компонент к--л. состояния атома. В принципе такое устройство аналогично обычному
двухлучевому оптич. интерферометру.
Принцип действия атомного интерферометра может быть пояснён
следующим примером. Пучок атомов водорода в метастабиль-ном состоянии 2S1/2
последовательно проходит через две пространственно разделённые зоны 1 и
2, внутри к-рых атомы подвергаются воздействию неадиабатич. возмущения,
вследствие чего становятся возможными их переходы в др. состояния, напр. 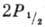 и
и 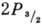 . Возмущающим
фактором является электрич. поле, локализованное в пространстве между зонами
(рис. 1), к-рое резко изменяется на границах, т. е. в пределах каждой
зоны ширины d.
. Возмущающим
фактором является электрич. поле, локализованное в пространстве между зонами
(рис. 1), к-рое резко изменяется на границах, т. е. в пределах каждой
зоны ширины d.
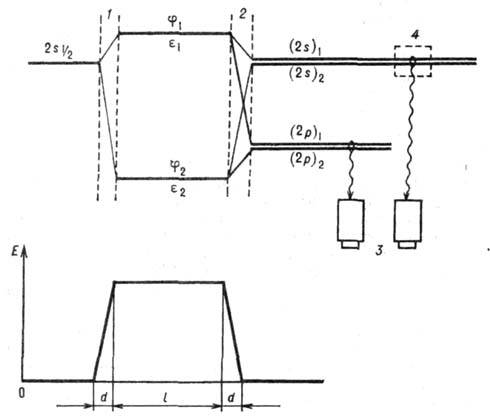
Рис. 1. Схема атомного интерферометра:
1 и 2 -входная и выходная электродные системы, 3-детекторы
La-излучения,
4 - область действия дополнительного электрич. поля.
Для упрощения картины можно
ограничиться рассмотрением двухуровневой системы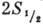 -
- 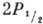 , что оправдано
при не слишком сильных полях; в этом случае влияние уровня
, что оправдано
при не слишком сильных полях; в этом случае влияние уровня 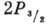 сказывается слабо и может быть учтено малыми поправками. При пересечении первой
границы атомы переходят в суперпозицию собств. состояний
сказывается слабо и может быть учтено малыми поправками. При пересечении первой
границы атомы переходят в суперпозицию собств. состояний 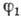 и
и 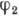 с энергиями
с энергиями 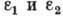 ,
определяемыми величиной напряжённости
электрич. поля E. На границе зоны 2, где поле убывает до нуля,
возникнут компоненты пучка, представляющие как состояние
,
определяемыми величиной напряжённости
электрич. поля E. На границе зоны 2, где поле убывает до нуля,
возникнут компоненты пучка, представляющие как состояние 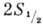 , так и состояние
, так и состояние 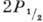 ,
причем каждый из термов
,
причем каждый из термов 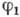 и
и 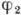 даст начало паре
таких состояний.
даст начало паре
таких состояний.
По выходе из поля амплитуды (здесь уже
собственных) состояний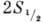 и
и 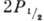 будут определяться
амплитудами переходов и разностью фаз между компонентами каждой пары Эта разность
зависит от времени пролета в поле и от частоты перехода между термами
будут определяться
амплитудами переходов и разностью фаз между компонентами каждой пары Эта разность
зависит от времени пролета в поле и от частоты перехода между термами 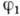 и
и 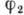 , расщеплёнными
электрич. полем (Штарка эффект ).Поскольку величина расщепления определяется
напряженностью поля Е, то при ее монотонном изменении в прошедшем пучке
будут наблюдаться периодические (происходящие в противофазе) колебания интенсивности
потоков 2S- и 2Р-атомов, обусловленные интерференцией компонент каждой пары:
(2S)1-(2S)2 и (2P)1-(2P)2. Такое же явление будет наблюдаться при изменении времени пролета t,
определяемого расстоянием l между границами поля (l>d).
, расщеплёнными
электрич. полем (Штарка эффект ).Поскольку величина расщепления определяется
напряженностью поля Е, то при ее монотонном изменении в прошедшем пучке
будут наблюдаться периодические (происходящие в противофазе) колебания интенсивности
потоков 2S- и 2Р-атомов, обусловленные интерференцией компонент каждой пары:
(2S)1-(2S)2 и (2P)1-(2P)2. Такое же явление будет наблюдаться при изменении времени пролета t,
определяемого расстоянием l между границами поля (l>d).
Наблюдение картины интерференции можно
осуществить измерением потока короткоживущих 2P-атомов. Детектор, расположенный
за второй границей, будет регистрировать фотоны, отвечающие переходу 2Р-1S,
т. е. головную линию серии Лаймана 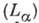 с длиной волны 1216
с длиной волны 1216 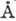 .
Можно также наблюдать происходящую в противофазе интерференцию 2S-компонент,
для чего необходимо пропустить пучок 2S-атомов через дополнит. электрич. поле,
перемешивающее состояния 2S и 2Р.
.
Можно также наблюдать происходящую в противофазе интерференцию 2S-компонент,
для чего необходимо пропустить пучок 2S-атомов через дополнит. электрич. поле,
перемешивающее состояния 2S и 2Р.
В двухуровневой системе 2S1/2-2P1/2,
имеют место переходы между S- и Р-подуровнями сверхтонкой структуры с проекциями Fz квантового числа суммарного момента F ядра и электрона, равными 1,0 и -1 (рис. 2). T. к. разности энергий для
переходов с 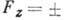 1 (согласно
отбора правилам)совпадают, результирующая интенсивность 2Р-компоненты
пучка будет определяться суммой трёх слагаемых, соответствующих этим
переходам:
1 (согласно
отбора правилам)совпадают, результирующая интенсивность 2Р-компоненты
пучка будет определяться суммой трёх слагаемых, соответствующих этим
переходам: 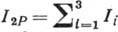 . Если положить х=<d>
. Если положить х=<d>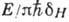 ,
где <d> - матричный элемент перехода 2S1/2-2P1/2, a
,
где <d> - матричный элемент перехода 2S1/2-2P1/2, a 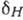 -лэмбовский
сдвиг, то вероятность выхода
-лэмбовский
сдвиг, то вероятность выхода 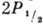 -атомов
для каждой i-й компоненты будет определяться выражением вида
-атомов
для каждой i-й компоненты будет определяться выражением вида
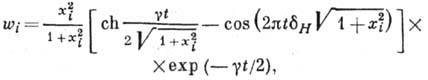
где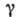 -постоянная
распада 2Р-состояния.
-постоянная
распада 2Р-состояния.
Атомный интерферометр представляет собой помещенную
в вакуум систему из 2 электродов (создающих неадиабатически изменяющееся на
границах поле), длина к-рой зависит от скорости атомов пучка и составляет обычно
1-50 см. Особенности тонкой структуры 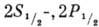 -уровней атомов водорода оптимально проявляются при х~1, чему соответствует
E ~ 300 В/см.
-уровней атомов водорода оптимально проявляются при х~1, чему соответствует
E ~ 300 В/см.
На рис. 3 показаны кривые интерференции
компонент 2Р-состояния атома водорода (являющейся оптич. аналогом эффекта Пайса
- Пиччони для системы 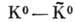 ; см, К-мезоны).
; см, К-мезоны).
Наблюдение атомных состояний в течение
длительного времени при помощи А. и. позволяет осуществить качественно новые
эксперименты, поскольку картина интерференции, зарегистрированная в широком
интервале сдвига фаз, чрезвычайно
чувствительна к характеристикам её компонент.
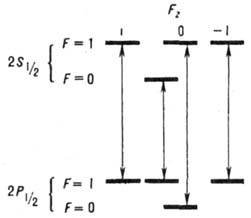
Рис. 2. Сверхтонкая структура 2S1/2
-, 2Р1/2
-уровней атома водорода (масштаб не выдержан)
Одним из примеров применения А. и.
является измерение лэмбовского сдвига в атоме водорода. Из
ф-лы для двухэлектродного интерферометра следует, что аксперим. зависимость
выхода 2Р-атомов от E и
t позволяет в принципе найти величину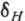 .
.
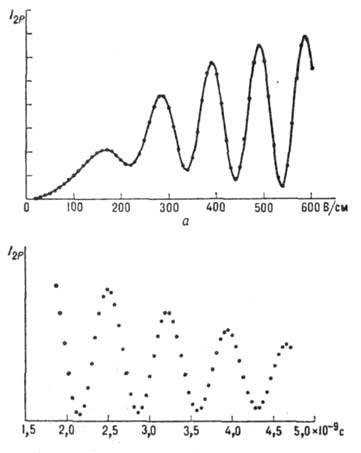
Рис. 3. Зависимость интенсивности 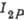 компоненты 2Р от напряжённости электрич. поля E для времени пролёта t=2,5512*l0-9
с (а) и от t при E = 400 В/см (б).
компоненты 2Р от напряжённости электрич. поля E для времени пролёта t=2,5512*l0-9
с (а) и от t при E = 400 В/см (б).
Однако определение её с точностью ~10-6
оказывается затруднительным из-за сложного поведения атома в поле и неопределённости
характеристик этого поля, особенно вблизи отверстий в электродах для прохода
пучка.
Для точного измерения 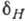 применяется т. н. двойной А. и. с двумя двухэлектродными системами (типа, изображённого
на рис. 1), разделёнными промежутком L. Атом водорода в состоянии
применяется т. н. двойной А. и. с двумя двухэлектродными системами (типа, изображённого
на рис. 1), разделёнными промежутком L. Атом водорода в состоянии 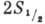 , пролетающий через такой интерферометр, последовательно подвергается действию
неадиабатич. полей во входной и выходной электродных системах, к-рое приводит
к перемешиванию состояний 2S и 2Р. Роль первой системы сводится
к созданию суперпозиции 2S-, 2Р-состояний из исходного состояния 2S. Для того
чтобы экспериментально найти сдвиг фаз 2S- и 2Р-компонент пучка после пролёта
атомом расстояния L, используется, в качестве анализатора, вторая двухэлектродная
система, образующая компоненты 2Р-состояния как из 2P-, так и из 2S-состояний.
Интерференцию этих компонент наблюдают при помощи детектора La-квантов.
, пролетающий через такой интерферометр, последовательно подвергается действию
неадиабатич. полей во входной и выходной электродных системах, к-рое приводит
к перемешиванию состояний 2S и 2Р. Роль первой системы сводится
к созданию суперпозиции 2S-, 2Р-состояний из исходного состояния 2S. Для того
чтобы экспериментально найти сдвиг фаз 2S- и 2Р-компонент пучка после пролёта
атомом расстояния L, используется, в качестве анализатора, вторая двухэлектродная
система, образующая компоненты 2Р-состояния как из 2P-, так и из 2S-состояний.
Интерференцию этих компонент наблюдают при помощи детектора La-квантов.
Процессы, происходящие в интерферометре,
удобно рассматривать в системе покоящегося атома. В этом случае на атом будут
действовать два импульса электрич. поля, разделённые промежутком времени t=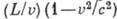 , где
, где 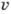 -скорость атома.
В промежутке между электродными системами, т. е. в области, где поля нет, состояния
2S и 2Р являются собственными и их эволюция определяется точно.
-скорость атома.
В промежутке между электродными системами, т. е. в области, где поля нет, состояния
2S и 2Р являются собственными и их эволюция определяется точно.
Поэтому можно написать точное выражение
для вероятности выхода 2Р-атомов после пролёта через двойной 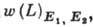 интерферометр как функции длины L или времени пролёта t (E1,
E2 - величины напряжённостей электрич. полей во входной и выходной
двухэлектродных системах). Существенно, что при эксперим. определении зависимости
интерферометр как функции длины L или времени пролёта t (E1,
E2 - величины напряжённостей электрич. полей во входной и выходной
двухэлектродных системах). Существенно, что при эксперим. определении зависимости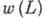 в качестве переменной L можно взять не абс. значение длины, а её приращение,
отсчитанное от некрой произвольной точки.
в качестве переменной L можно взять не абс. значение длины, а её приращение,
отсчитанное от некрой произвольной точки.

Ю. Л. Соколов
|
|