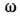в лабораторной
системе координат распространяется по оси z (колебания Е-волны происходят
в плоскости ху):Джонса матричный метод - способ описания амплитуды, фазы и состояния поляризации плоских монохроматич.
(т. е. когерентных) эл--магн. волн, проходящих через оптич. системы, обладающие
двойным лучепреломлением и дихроизмом .Метод предложен P. Джонсом
[1] и базируется на двух понятиях: вектора Джонса, характеризующего состояние
светового потока, и матрицы (оператора) Джонса, описывающей свойства оптич.
системы. Физ. основой Д. м. м. является линейность ур-ний эл--магн. поля и ур-ний
связи, позволяющая применять аппарат линейной матричной алгебры. Д. м. м. часто
используется для расчёта поляризац. систем, особенно в лазерной технике.
Пусть эл--магн. волна частоты
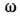в лабораторной
системе координат распространяется по оси z (колебания Е-волны происходят
в плоскости ху):
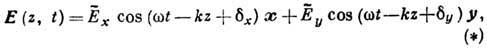
где k - волновой
вектор,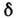 
- нач.
фаза. Тогда E(z, t)можно представить в виде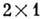 
вектор-столбца:
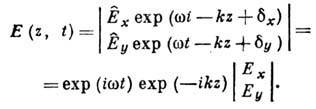
Ограничиваясь (как обычно
в оптике) рассмотрением стационарных процессов, можно отбросить временной множитель
и пользоваться кратким символич. обозначением:
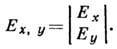
Интенсивность волны
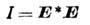
(* - комплексное сопряжение).
Поскольку в рамках линейной
оптики величина абс. интенсивности не существенна, для упрощения ф-л можно "нормировать"
векторы, полагая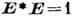 
. В таких обозначениях вектор Джонса волны, линейно поляризованной по оси х или у, будет соответственно
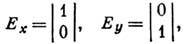
а волны правополяризованной
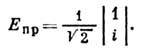
В общем случае два ортогональных
вектора Джонса описывают две эллиптически поляризованные волны, эллипсы к-рых
противоположны по направлению обхода и имеют взаимно перпендикулярные оси (т.
е. наиболее общий случай полной поляризации когерентных световых потоков).
Построение матриц Джонса
можно проиллюстрировать примером со световой волной, падающей нормально на пластинку
из одноосного кристалла, оптич. ось к-рого х' лежит в плоскости ху и составляет с осью
х угол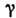 
.
На выходе из пластинки вектор поля Евых можно записать в виде
матрицы:
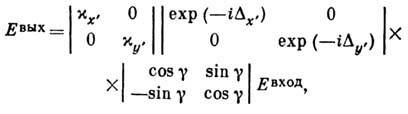
где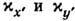 
- коэф. поглощения, а 
-
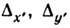сдвиги фаз, вносимые пластинкой, или
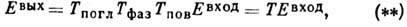
где Тпогл
- матрица поглощения, Тфаз - матрица фазового сдвига, Тпов
- "матрица поворота". Если волна затем проходит через вторую пластинку,
аналогичная запись примет вид:
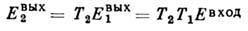
и т. д. Именно в этом и
состоит осн. удобство метода, позволяющего при расчёте многоэлементных систем
мультиплицировать как независимые результаты изменения поля волны при прохождении
через каждый элемент системы. Вычисление T для отд. элементов обычно
несложно; для большого количества типичных элементов имеются таблицы [2, 3].
Матрица поворота имеет одинаковый вид для всех элементов.
Если среди элементов оптич.
системы есть отражательный анизотропный элемент (напр., отражение внутри одноосного
кристалла), "матрица отражения" имеет вид:
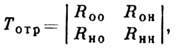
где индексы о и н относятся
соответственно к обыкновенному и необыкновенному лучам (первый - к падающему,
второй - к отражённому), а коэффициенты Rij определяются по
Френеля формулам.
Д. м. м. может, естественно,
строиться не только на линейных единичных базисных векторах, как в (*), но и
на круговых или эллиптич. единичных векторах, в зависимости от характера задачи
[3].
Д. м. м. удобен тем, что
позволяет выделить изолированно информацию о поляризации волны - т. н. поляризационную
передаточную функцию системы. Эллипсы поляризации на входе и выходе полностью
описываются комплексными числами
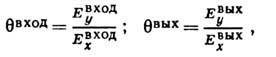
и если записать (**) в
развёрнутом виде, получим
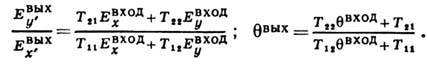
T. о., эллипс колебаний
на выходе определяется только эллипсом колебаний на входе. Аналогично можно
ввести передаточную функцию для фазы, для амплитуды.
Д. м. м. не применяется
для неоднородных волн и для световых пучков больших апертур. Д. м. м. непригоден
также для некогерентного света, но формализм его можно использовать для построения
матрицы когерентности [4]. Для описания состояния поляризации некогерентного
света используются методы Стокса параметров и Мюллера матриц.
В. А. Кизель
|
|
 |
