Евклидово пространство - конечномерное векторное пространство с положительно определённым скалярным произведением.
Является непосредств. обобщением обычного трёхмерного пространства. В
Е. п. существуют декартовы координаты, в к-рых скалярное произведение (ху)векторов х- (x1, . . . , хn)и y = (y1, . . . , yп)имеет вид (xy)=x1y1+. . .+хnуп. В произвольных координатах скалярное произведение по определению удовлетворяет условиям: 1) (хх)/0, (хх) = 0 лишь при x=0; 2) (ху) = (ух)*; 3) (aху) = a(ху); 4) (x{y+z}) =(xy)+ (xz), где a - любое комплексное число, * означает комплексное сопряжение. В Е. п. имеет место неравенство Коши - Буняковского |xу|2[(хх)(уу). Число
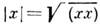
наз. нормой (или длиной)
вектора х, а угол q между векторами х, у находят из ф-лы cosq= (xy)/|x| |у|.
Первоначально евклидовыми наз. пространства, в к-рых выполнены аксиомы
евклидовой геометрии, осн. понятиями к-рой являются длина векторов и
угол между ними. Бесконечномерное Е. п. обычно наз. гильбертовым пространством. Пространство, в к-ром нарушено условие 1) положительности скалярного произведения, наз. псевдоевклидовым пространством. Пространство, в к-ром п четно, а условие 2) заменяется условием (ху) = --(ух), наз. симплектическим пространством.
Знаете ли Вы, что, когда некоторые исследователи, пытающиеся примирить релятивизм и эфирную физику, говорят, например, о том, что космос состоит на 70% из "физического вакуума", а на 30% - из вещества и поля, то они впадают в фундаментальное логическое противоречие. Это противоречие заключается в следующем.
Вещество и поле не есть что-то отдельное от эфира, также как и человеческое тело не есть что-то отдельное от атомов и молекул его составляющих. Оно и есть эти атомы и молекулы, собранные в определенном порядке. Также и вещество не есть что-то отдельное от элементарных частиц, а оно состоит из них как базовой материи. Также и элементарные частицы состоят из частиц эфира как базовой материи нижнего уровня. Таким образом, всё, что есть во вселенной - это есть эфир. Эфира 100%. Из него состоят элементарные частицы, а из них всё остальное. Подробнее читайте в FAQ по эфирной физике.