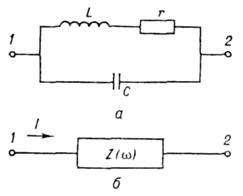
Рис. 1. Электрическая цепь, включающая пассивные линейные элементы и имеющая два полюса: a - схема цепи; б - эквивалентный двухполюсник с импедансом Z(w).
Понятие импеданса было введено в электродинамику О. Хевисайдом (О. Heaviside) и
О. Лоджем (О. Lodge), понятие полевого импеданса - С. Щелкуновым (S.
Schelkunoff, 1938). Импедансные характеристики используют не только в электродинамике, их вводят для описания
линий передачи волновых возмущений любой природы (см., напр., Импеданс акустический).
Импеданс двухполюсника. В теории электрич. цепей любую часть цепи, состоящую из пассивных линейных элементов (таких, как сопротивления r, индуктивности L, ёмкости С,
трансформаторы) и имеющую две точки (полюса) подключения к остальной
цепи (рис. 1), в случае квазистационарных гармонич. процессов с
зависимостью от временя ~exp(iwt) можно рассматривать как пассивный
двухполюсник, все внеш. свойства к-рого описываются одной комплексной
величиной Z, наз. импеданса двухполюсника и равной
Z (w) = V/I =R (w) + iX(w).

Рис. 1. Электрическая цепь, включающая пассивные линейные элементы и
имеющая два полюса: a - схема цепи; б - эквивалентный двухполюсник с импедансом Z(w).
Здесь V - комплексная амплитуда напряжения между полюсами 1 и 2, I - комплексная амплитуда тока в направлении от полюса 1 к полюсу 2; R - веществ. часть импеданса (активное сопротивление), X - мнимая часть импеданса
(реактивное сопротивление, реактанс). Модуль импеданса |Z|=(R2+X2)1/2 наз. полным сопротивлением двухполюсника. В СИ импеданс измеряется в Омах, в Гаусса системе единиц имеет размерность, обратную скорости. Иногда наряду с импедансом Z используют обратную ему величину s=Z-1, наз. адмитансом.
Активное сопротивление R ответственно за потери энергии, поступающей в двухполюсник. Мощность потерь Р (средняя за период колебаний Т=2p/w)выражается соотношением
Р =R|I|2/2.
Реактанс характеризует величину энергии, пульсирующей с частотой 2w (и
потому в среднем за период равной нулю), накапливаемой в двухполюснике и
отдаваемой обратно источнику. Знак реактанса определяется зависимостью
от времени: в технике и прикладной физике (и в данной статье) полагают
её
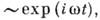 в теоретич.
физике обычно принимают
в теоретич.
физике обычно принимают
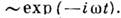 В случае чисто индуктивного двухполюсника (индуктивное сопротивление) Х=ХL=wL (в СИ; в системе единиц Гаусса XL=c-2wL), а для чисто ёмкостного (ёмкостное сопротивление) Х=Хс=-(wС)-1. Различие в знаках порождается дуальной асимметрией Максвелла уравнений (Е''H, Н''- E)и
отражает соотношение между фазами напряжений и токов: ток в идеальной
катушке самоиндукции отстаёт по фазе на p/2 от приложенного напряжения, а
ток через идеальный конденсатор опережает па тот же угол напряжение,
создаваемое на его обкладках. Правила сложения импеданса при последоват. и параллельном их соединении такие же, как и в случае обычных омических
сопротивлений: при последоват. соединении двухполюсников складываются импедансы
Z, а при параллельном - адмитансы Z-l. Напр., для двухполюсника, изображённого на рис. la, имеем:
В случае чисто индуктивного двухполюсника (индуктивное сопротивление) Х=ХL=wL (в СИ; в системе единиц Гаусса XL=c-2wL), а для чисто ёмкостного (ёмкостное сопротивление) Х=Хс=-(wС)-1. Различие в знаках порождается дуальной асимметрией Максвелла уравнений (Е''H, Н''- E)и
отражает соотношение между фазами напряжений и токов: ток в идеальной
катушке самоиндукции отстаёт по фазе на p/2 от приложенного напряжения, а
ток через идеальный конденсатор опережает па тот же угол напряжение,
создаваемое на его обкладках. Правила сложения импеданса при последоват. и параллельном их соединении такие же, как и в случае обычных омических
сопротивлений: при последоват. соединении двухполюсников складываются импедансы
Z, а при параллельном - адмитансы Z-l. Напр., для двухполюсника, изображённого на рис. la, имеем:
Z-1 = (r+ iwL)-1+iwC.
Матрица импеданса. Разветвлённую электрич. цепь,
имеющую более двух точек подключения, наз. многополюсником [если число
пар точек подключения (входов) равно N, то цепь наз. 2N-полюсником].
На входах многополюсника должны быть заданы направления отсчёта
напряжений и токов (рис. 2). Если многополюсник включает в себя только
линейные, пассивные и
взаимные элементы, то для квазистационарных гармонич. процессов все его
внеш. свойства описываются матрицей импеданса ||Zab||, связывающей комплексные амплитуды напряжений и токов на входах при произвольном подключении к когерентным источникам:
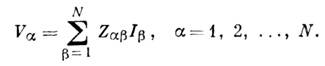
Напр., для четырёхполюсника, изображённого на рис. 3, а, элементы матрицы импеданса равны: Z11=Z1+Z3, Z22=Z2+Z3, Z12=Z21=Z3. В силу взаимности принципа матрица ||Zab|| симметрична, т. е. Zab=Zba
Входной импеданс. Свойства многополюсников можно описать и с
помощью т. н. входных импедансов отд. входов.
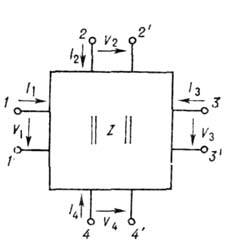
Рис. 2. Многополюсник, все внешние свойства которого задаются матрицей импеданса ||Z||.
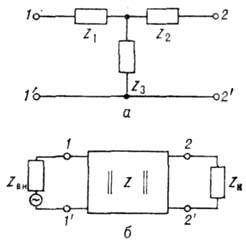
Рис. 3. Четырёхполюсник: a - эквивалентная схема; б - схема для определения входного импеданса.
При этом по отношению к выбранному входу многополюсник рассматривают как
двухполюсник, а все остальные входы считают нагруженными произвольными
импедансами Zнb. Поэтому входные импедансы являются функциями не только частоты, но и нагрузочных импедансов.
Так, для четырёхполюсника, приведённого на рис. 3:
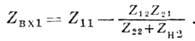
Для согласования произвольной нагрузки Zн с источником, имеющим внутренний импеданс Zвн, используют недиссипативные четырёхполюсники (без поглощающих элементов), добиваясь выполнения условия Zвх(Zн)=Z*вн (*
означает комплексное сопряжение). При этом достигается макс. передача
энергии от источника к нагрузке (кпд равен 50%, остальная энергия
поглощается внутри источника). Если требуется обеспечить высокий кпд
передачи, выбирают такой согласующий четырёхполюсник, чтобы выполнялись
условия: Rвх(Zн)дRвн, Xвх(Zн)=-Хвн.
Волновой импеданс. Входной импеданс четырёхполюсника, удовлетворяющий условию Zвх(Zн=Zв)=Zн= Zв,
наз. волновым импедансом, ибо в бесконечной цепочке, составленной из
одинаковых четырёхполюсников, будут без отражений распространяться волны
(в общем случае экспоненциально затухающие) с пост. значением отношения
напряжения к току. В пределе непрерывной однородной линии передачи это
отношение в любой нормальном сечении постоянно и при отсутствии потерь
равно Zв = (Lп/Cп)1/2, где Lп, Сп - погонные (на единицу длины) индуктивность и ёмкость лииии.
Для линии конечной длины, нагруженной на Zн№Zв, коэф. отражения (отношение комплексных амплитуд отражённой и падающей волн) равен
Г=(Zн-Zв)/(Zн+Zв). (1)
При Zн=0 и Zн'':, что соответствует
короткозамкнутой и разомкнутой линиям, имеет место полное отражение
(Г=71). Длинные линии не являются квазистационарными системами, поэтому
понятие напряжения является условным. Обычно его относят только к
точкам, лежащим в одном нормальном сечении линии Sn, а путь
интегрирования g12 выбирают лежащим в этом же сечении
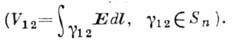
Поверхностный (полевой) импеданс 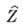 вводят для
монохроматич. эл--магн. полей Е(r)exp(iwt), H(r)exp(iwt) на любой условной поверхности S след. образом:
вводят для
монохроматич. эл--магн. полей Е(r)exp(iwt), H(r)exp(iwt) на любой условной поверхности S след. образом:
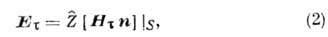
где Et, Нt - тангенц. составляющие напряжённостей электрич. и магн. поля, п - единичная нормаль к S, её направление выбирают обычно так, чтобы проекция на неё среднего по времени потока энергии (вектора Пойнтинга П=(с/8p)Rе [ЕН*] была положительна. Входящий в (2) импеданс 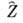 в общем случае является тензором, компоненты к-рого зависят от поляризации поля. В тех случаях, когда Еt и Нt
взаимно перпендикулярны, вводят скалярный полевой импеданс Z. В гауссовых
единицах полевой импеданс безразмерен, а в СИ имеет размерность сопротивления.
Иногда для импеданса в системе единиц Гаусса используют выражение
в общем случае является тензором, компоненты к-рого зависят от поляризации поля. В тех случаях, когда Еt и Нt
взаимно перпендикулярны, вводят скалярный полевой импеданс Z. В гауссовых
единицах полевой импеданс безразмерен, а в СИ имеет размерность сопротивления.
Иногда для импеданса в системе единиц Гаусса используют выражение 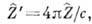 при этом
при этом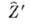 имеет размерность сопротивления.
Эл--магн. волны разных типов (моды) характеризуются разл. полевыми импедансами,
задаваемыми на волновых фронтах. Так, для поперечной плоской волны (типа
ТЕМ), распространяющейся в направлении п в изотропной среде или в волноводе,
имеет размерность сопротивления.
Эл--магн. волны разных типов (моды) характеризуются разл. полевыми импедансами,
задаваемыми на волновых фронтах. Так, для поперечной плоской волны (типа
ТЕМ), распространяющейся в направлении п в изотропной среде или в волноводе,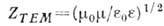 (m, e - относительные магн. и диэлектрич. проницаемости среды, e0, m0 - проницаемости вакуума, в системе единиц Гаусса e0=m0=1). В вакууме
(m, e - относительные магн. и диэлектрич. проницаемости среды, e0, m0 - проницаемости вакуума, в системе единиц Гаусса e0=m0=1). В вакууме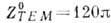 Ом, эта размерная константа наз. характеристич. импедансом вакуума (в системе единиц Гаусса
Ом, эта размерная константа наз. характеристич. импедансом вакуума (в системе единиц Гаусса 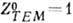 ). Для волн типа ТМ и ТЕ соответствующие импедансы таковы:
). Для волн типа ТМ и ТЕ соответствующие импедансы таковы:
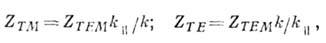
где k - волновое число, k|| - продольная компонента волнового вектора. Для критич. частот (k||''0) ZTM''0, ZTE'':, a для закритических, когда волна превращается в экспоненциально убывающую моду:
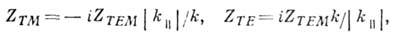
т. е. в первом случае речь идёт о преимуществ. запасе электрич. энергии (ёмкостный импеданс), во втором - магнитной (индуктивный импеданс).
При отсутствии потерь полевой импеданс для распространяющихся волн - величина действительная; иногда её наз. волновым сопротивлением
среды, поскольку она обладает мн. свойствами волнового сопротивления
линии или цепочки четырёхполюсников. В частности, при падении плоской
волны из среды 1 на плоскую границу раздела со средой 2 коэф. отражения
(по амплитудам полей) аналогично (1) выражается в виде
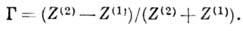
Это выражение представляет собой Френеля формулы, записанные через импеданс (р-поляризации соответствует мода ТМ, s-поляризации - мода ТЕ, (k||/k)(1,2)=cosq(l,2), q(l) и q(2)
- углы падения и преломления). При исследовании отражения от
плоскослоистых неоднородных сред часто ур-ния для полей преобразуют в
ур-ния для полевых импедансов, при этом порядок ур-ний понижается. Существенны
т. н. импедансные поверхности, т. е. поверхности с заданным,
фиксированным на них значением полевого импеданса Фактически фиксация
осуществляется (в большинстве случаев приближённо), когда структура поля
"под поверхностью" неизменна и определяется к--л. свойствами среды или
формирующих поле устройств. Так, при падении волны на хорошо поглощающую
среду волна уходит в глубь среды почти по нормали, независимо от угла
падения, следовательно, "входной" импеданс можно считать фиксированным и
равным Z(2)TEM (Леонтовича граничное условие). С помощью импедансных поверхностей моделируют границы направляющих устройств в антеннах, замедляющих системах и т. д.

|
|