Рис. 1. Кольца Гука в отражённом свете.
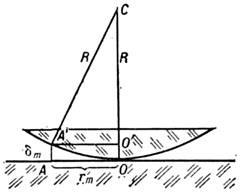
Рис. 2. Схема образования колец Гука:
О - точка касания сферы радиуса R и плоской поверхности;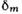 - толщина воздушного зазора в области образования кольца радиуса rm.
- толщина воздушного зазора в области образования кольца радиуса rm.
Знаете ли Вы, в чем фокус эксперимента Майкельсона?
Эксперимент А. Майкельсона, Майкельсона - Морли - действительно является цирковым фокусом, загипнотизировавшим физиков на 120 лет.
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
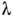 Н. к. представляют собой чередующиеся тёмные и светлые полосы (рис. 1).
Светлые возникают в местах, где разность фаз между прямым и дважды отражённым
лучом (в проходящем свете) или между лучами, отражёнными от обеих соприкасающихся
поверхностей (в отражённом свете), равна
Н. к. представляют собой чередующиеся тёмные и светлые полосы (рис. 1).
Светлые возникают в местах, где разность фаз между прямым и дважды отражённым
лучом (в проходящем свете) или между лучами, отражёнными от обеих соприкасающихся
поверхностей (в отражённом свете), равна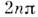 (п
= 1, 2, 3, ...) (т. е. разность хода
(п
= 1, 2, 3, ...) (т. е. разность хода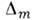 равна чётному числу полуволн). Тёмные кольца образуются там, где разность
фаз равна
равна чётному числу полуволн). Тёмные кольца образуются там, где разность
фаз равна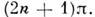 Разность фаз лучей определяется толщиной зазора
Разность фаз лучей определяется толщиной зазора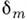 с учётом изменения фазы световой волны при отражении (см. Отражение
света). Так, при отражении от границы воздух - стекло фаза меняется
на
с учётом изменения фазы световой волны при отражении (см. Отражение
света). Так, при отражении от границы воздух - стекло фаза меняется
на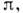 а при
отражении от границы стекло - воздух фаза остаётся неизменной. Поэтому
в случае двух стеклянных поверхностей (рис. 2), с учётом различий в условиях
отражения от ниж. и верх. поверхностей зазора (потеря полуволны), т-етёмное
кольцо образуется, если
а при
отражении от границы стекло - воздух фаза остаётся неизменной. Поэтому
в случае двух стеклянных поверхностей (рис. 2), с учётом различий в условиях
отражения от ниж. и верх. поверхностей зазора (потеря полуволны), т-етёмное
кольцо образуется, если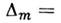
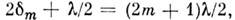 т. е. при толщине зазора
т. е. при толщине зазора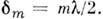 Радиус rт т-го кольца определяется из треугольника
А-О-С:
Радиус rт т-го кольца определяется из треугольника
А-О-С: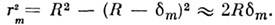

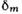 - толщина воздушного зазора в области образования кольца радиуса rm.
- толщина воздушного зазора в области образования кольца радиуса rm.
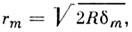 для тёмного m-го кольца rт =
для тёмного m-го кольца rт =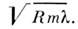 Это
соотношение позволяет с хорошей точностью определять
Это
соотношение позволяет с хорошей точностью определять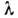 по
измерениям rт. Если
по
измерениям rт. Если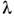 известна, Н. к. можно использовать для измерения радиусов поверхностей
линз и контроля правильности формы сферич. и плоских поверхностей. При
освещении немоно-хроматич. (напр., белым) светом Н. к. становятся цветными.
Наиб. отчётливо Н. к. наблюдаются при малой толщине зазора (т. е. при использовании
сферич. поверхностей больших радиусов).
известна, Н. к. можно использовать для измерения радиусов поверхностей
линз и контроля правильности формы сферич. и плоских поверхностей. При
освещении немоно-хроматич. (напр., белым) светом Н. к. становятся цветными.
Наиб. отчётливо Н. к. наблюдаются при малой толщине зазора (т. е. при использовании
сферич. поверхностей больших радиусов).
