Преобразование Радона - интегральное преобразование
функции f(x)от n вещественных переменных, x = (х1,
..., хп), ставящее в соответствие функции f(x)её интеграл
по (п - 1)-мерной плоскости (гиперплоскости) П = {x х
= С} (хотя бы один из вещественных параметров x i,
задающих положение П в Rn, не равен 0):
где dVп - евклидов элемент
объёма на П.
Преобразование Радона F(x, С)функции f(x)- однородная функция своих переменных степени -1, связанная с Фурье преобразованиемфункции
f(x)ф-лой
Ф-лы обращения Р. п. различны для чётных и нечётных
п: для чётных n
для нечётных n
Здесь Г - произвольная поверхность в пространстве
параметров x, окружающая начало координат, а
Символом
обозначена (n-1)-я производная Р. п. по
последнему аргументу.
Ф-лы обращения решают задачу восстановления функции
по значениям её интегралов, взятых по всем гиперплоскостям пространства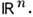Эта
задача возникает, напр., в томографии, где f(x) характеризует
поглощение звука в данной точке c исследуемого объёма, а непосредственно
измеряется её Р. п.- интегральные характеристики поглощения в последовательных
плоских сечениях.
Литература по преобразованию Радона
Гельфанд И. М., Граев М. И., Виленкин Н. Я., Интегральная геометрия, М., 1962;
Функциональный анализ, под ред. С. Г. Крейна, М., 1964.
Знаете ли Вы, что, как и всякая идолопоклонническая религия, релятивизм представляет собой инструмент идеологического подчинения одних людей другим с помощью абсолютно бессовестной манипуляции их психикой для достижения интересов определенных групп людей, стоящих у руля этой воровской машины? Подробнее читайте в FAQ по эфирной физике.
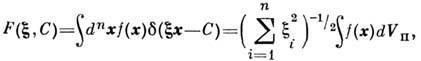
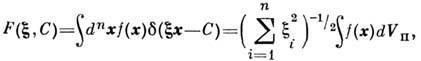
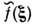функции
f(x)ф-лой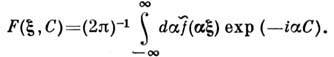
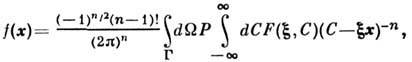
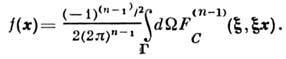
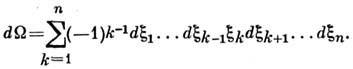
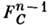обозначена (n-1)-я производная Р. п. по
последнему аргументу.
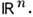Эта
задача возникает, напр., в томографии, где f(x) характеризует
поглощение звука в данной точке c исследуемого объёма, а непосредственно
измеряется её Р. п.- интегральные характеристики поглощения в последовательных
плоских сечениях.
