Знаете ли Вы, что любой разумный человек скажет, что не может быть улыбки без кота и дыма без огня, что-то там, в космосе, должно быть, теплое, излучающее ЭМ-волны, соответствующее температуре 2.7ºК. Действительно, наблюдаемое космическое микроволновое излучение (CMB) есть тепловое излучение частиц эфира, имеющих температуру 2.7ºK. Еще в начале ХХ века великие химики и физики
Д. И. Менделеев и Вальтер Нернст предсказали, что такое излучение (температура) должно обнаруживаться в космосе. В 1933 году проф. Эрих Регенер из Штуттгарта с помощью стратосферных зондов
измерил эту температуру. Его измерения дали 2.8ºK - практически точное современное значение. Подробнее читайте в
FAQ по эфирной физике.
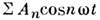 с частотами nw, кратными осн. частоте (где Ап - амплитуды
гармонич. функций, t - время, п - номер гармоники). Чем сильнее
исходное колебание отличается от гармонического, тем богаче его спектр,
тем больше составляющих обертонов (гармоник) содержится в разложении и
тем больше их амплитуды. В общем случае С. к. содержит бесконечный ряд
гармоник, амплитуды к-рых быстро убывают с увеличением их номера, так что
практически приходится принимать во внимание только нек-рое конечное число
обертонов. Процессы, не имеющие строгой периодичности, или непериодические
могут представляться в виде суммы гармонич. компонентов с некратными частотами
или в виде суммы (интеграла) бесконечного числа составляющих со сколь угодно
близкими частотами (непрерывный спектр).
с частотами nw, кратными осн. частоте (где Ап - амплитуды
гармонич. функций, t - время, п - номер гармоники). Чем сильнее
исходное колебание отличается от гармонического, тем богаче его спектр,
тем больше составляющих обертонов (гармоник) содержится в разложении и
тем больше их амплитуды. В общем случае С. к. содержит бесконечный ряд
гармоник, амплитуды к-рых быстро убывают с увеличением их номера, так что
практически приходится принимать во внимание только нек-рое конечное число
обертонов. Процессы, не имеющие строгой периодичности, или непериодические
могут представляться в виде суммы гармонич. компонентов с некратными частотами
или в виде суммы (интеграла) бесконечного числа составляющих со сколь угодно
близкими частотами (непрерывный спектр).
