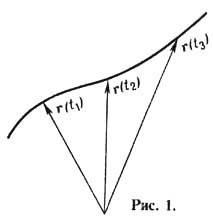
Траектория - кривая, к-рую описывает радиус-вектор r(t)координат тела с течением времени
(рис. 1). Понятие "Т." тесно связано с понятиями "материальная
точка" и "уравнения движения". Говорить о траектории имеет
смысл лишь в том случае,
когда размеры тела малы по сравнению с расстоянием, к-рое оно проходит.

Для определения функции r(t)
(а следовательно, и Т.) необходимо решить дифференц. ур-ние 2-го порядка, вытекающее
из 2-го закона Ньютона:
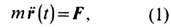
где т - масса тела,
F-действующая на него сила.
Ур-ние (1) при заданной
F определяет целое семейство траекторий. Выбор к--л. одной из
них осуществляется фиксацией нач. условий, роль к-рых обычно выполняют нач.
координаты и скорость тела,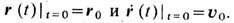 Напр., подставляя в качестве силы F в ф-лу (1) силу всемирного
тяготения,
Напр., подставляя в качестве силы F в ф-лу (1) силу всемирного
тяготения,

где G - гравитационная
постоянная, 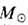 -масса
Солнца, т - масса его спутника, n - единичный вектор, направленный
от спутника к Солнцу, r-расстояние между ними, и, решая ур-ние
(1), можно доказать [И. Ньютон (I. Newton, 1684)], что Т. движения спутника
в зависимости от нач. условий является эллипсом, параболой или гиперболой.
-масса
Солнца, т - масса его спутника, n - единичный вектор, направленный
от спутника к Солнцу, r-расстояние между ними, и, решая ур-ние
(1), можно доказать [И. Ньютон (I. Newton, 1684)], что Т. движения спутника
в зависимости от нач. условий является эллипсом, параболой или гиперболой.
В классич. механике, если
известны координаты и скорость тела в к--л. момент времени, то Т. движения [функция
r(t)] однозначно определяется законом движения (1).
Представление о Т. движения
тела как о нек-рой гладкой кривой, к-рую можно найти, решив ур-ние (1), является
чисто макроскопическим. Для микроскопич. тел это не так. Из основных постулатов
термодинамики следует, что независимо от природы действующих на тело
сил среднеквадратичная флуктуация скорости тела, находящегося в термодинамическом
равновесии с внеш. средой, описывается ф-лой
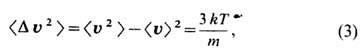
где k-постоянная
Больцмана, т - масса тела, Т-абс. темп-pa среды, в к-рую тело
помещено.
Величина 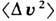 при комнатной температуре пренебрежимо мала для макроскопич. тел, но для отд. молекул
она составляет уже неск. сотен м в секунду. Поэтому Т. движения микроскопич.
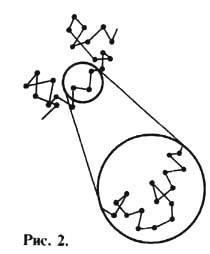
тела будет представлять собой хаотическую ломаную линию, подобную изображённой
на рис. 2. Это почти везде непрерывная и почти нигде недифференцируемая кривая.
Она называется б р о у н о вс к о й т р а е к т о р и е й (см.
Броуновское движение)и обладает тем свойством, что если увеличить любой
её фрагмент, то мы увидим такую же кривую. Т., изображённая на рис. 2, является
случайной, и имеет смысл говорить лишь о статистич. ансамбле таких Т. Полностью
определёнными являются только средние по ансамблю величины. Напр., квадрат ср.
смещения частицы <x2> как функция времени t есть
[А. Эйнштейн (A. Einstein), 1905]:
при комнатной температуре пренебрежимо мала для макроскопич. тел, но для отд. молекул
она составляет уже неск. сотен м в секунду. Поэтому Т. движения микроскопич.
тела будет представлять собой хаотическую ломаную линию, подобную изображённой
на рис. 2. Это почти везде непрерывная и почти нигде недифференцируемая кривая.
Она называется б р о у н о вс к о й т р а е к т о р и е й (см.
Броуновское движение)и обладает тем свойством, что если увеличить любой
её фрагмент, то мы увидим такую же кривую. Т., изображённая на рис. 2, является
случайной, и имеет смысл говорить лишь о статистич. ансамбле таких Т. Полностью
определёнными являются только средние по ансамблю величины. Напр., квадрат ср.
смещения частицы <x2> как функция времени t есть
[А. Эйнштейн (A. Einstein), 1905]:

где D - коэф. диффузии.
Броуновское движение является
заданным, если известна функция

к-рая имеет смысл вероятности
того, что частица, находящаяся в точке r1 в момент
времени t1 в момент t2 окажется в точке
r2.
В простейшем случае одномерного
броуновского движения функция (5) имеет вид
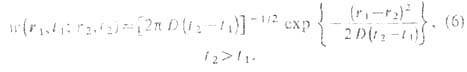
Т. о., для микроскопии,
тел Т. является статистич. понятием.
Для квантовых частиц понятие
"Т." утрачивает смысл. Количеств. критерием квантового движения
является условие

здесь 2p/h - постоянная
Планка, т - масса частицы (напр., электрона), u -характерная скорость,
L - характерный размер области движения частицы.
"Увидеть" Т.
движения квантовой частицы (напр., электрона в атоме) непосредственно при помощи
микроскопа или попытаться "поймать" Т. к--л. способом невозможно.
С формальной точки зрения причина состоит в том, что в квантовой частице неприменимо
понятие материальной точки, можно говорить лишь об амплитуде вероятности обнаружить
частицу в том или ином состоянии. Как показал-Кйзенберг (1927), физ. причина
такого положения вещей заключается в том, что, пытаясь измерить положение частицы,
мы неизбежно воздействуем на неё, причём это воздействие не может быть меньше
постоянной Планка. Следовательно, в квантовом случае [когда выполнено условие
(7)] представление о Т. как о геом. месте точек, в каждой из к-рых частицы имеют
определ. скорость, физически бессмысленно.
Несмотря на это, в 1947
Т. "вернулась" в квантовую механику благодаря остроумному формализму
интегрирования по траекториям, разработанному Р. Фейнманом (R. P. Feynman),
и, т. о., легла в основу его интерпретации квантовой механики (см. Фейнмана
представление в квантовой механике).
Оказывается, амплитуда
перехода квантовой частицы из точки r1,t1 в
точку r2,t2 можно записать в виде
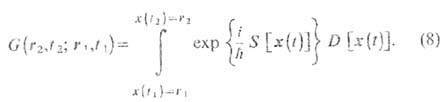
Здесь S[x(t)]
-действие классической частицы, движущейся по Т. х(t),
символ означает, что
необходимо просуммировать величину по всем Т., соединяющим точки r1,t1
и r2,t2. При этом величина 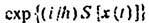 имеет смысл амплитуды вероятности того,
что частица попадёт из точки r1,t1 в точку
r2,t2, двигаясь по Т. x(t).
Т.о., суммируя амплитуды вероятности переходов
по всевозможным Т., мы получим амплитуду пере хода G квантовой
частицы (рис. 3).
имеет смысл амплитуды вероятности того,
что частица попадёт из точки r1,t1 в точку
r2,t2, двигаясь по Т. x(t).
Т.о., суммируя амплитуды вероятности переходов
по всевозможным Т., мы получим амплитуду пере хода G квантовой
частицы (рис. 3).
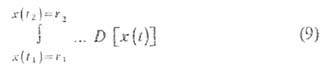
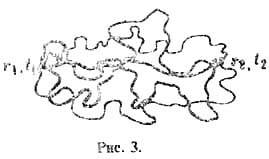
Ур-ние (1) определяет экстремальную
Т. в интеграле (8), к-рую называют классич. Т.
В классич. механике, к-рая описывает поведение мак-роскопич. тел, Т. движения является непосредственно измеряемой величиной. Для микроскопич. тел имеет смысл говорить лишь о статистическом ансамбле траекторий, поскольку для таких тел существенную роль играют термодинамич. флуктуации. И, наконец, в квантовой области представление о Т. как .о наблюдаемой физ. величине не имеет смысла. И всё же Т., уже как матсм. абстракция, образует основу очень красивого и плодотворного описания природы на квантовом уровне.

М. А. Савров
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|