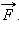 Под действием этой силы скорость тела изменилась на
Под действием этой силы скорость тела изменилась на 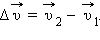 Следовательно, в
течение времени Δt тело двигалось с ускорением
Следовательно, в
течение времени Δt тело двигалось с ускорениемПусть на тело массой m в течение некоторого малого промежутка времени Δt
действовала сила 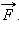 Под действием этой силы скорость тела изменилась на
Под действием этой силы скорость тела изменилась на 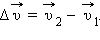 Следовательно, в
течение времени Δt тело двигалось с ускорением
Следовательно, в
течение времени Δt тело двигалось с ускорением
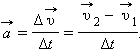 |
Из основного закона динамики следует:
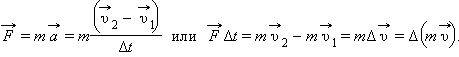 |
Физическая величина, равная произведению массы тела на скорость его
движения, называется импульсом тела (или количеством движения).
Импульс тела – векторная величина. Единицей измерения импульса в СИ является
килограмм-метр в секунду (кг·м/с). Физическая величина, равная
произведению силы на время ее действия, называется импульсом силы. Импульс силы
также является векторной величиной. Второй закон динамики может быть
сформулирован следующим образом: изменение импульса тела (количества
движения) равно импульсу силы. Обозначив импульс тела буквой 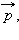 второй закон динамики можно записать в виде
второй закон динамики можно записать в виде
|
Именно в таком общем виде сформулировал второй закон динамики Роберт Гук. Сила
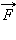 в этом
выражении представляет собой равнодействующую всех сил, приложенных к телу. Это
векторное равенство может быть записано в проекциях на координатные оси:
в этом
выражении представляет собой равнодействующую всех сил, приложенных к телу. Это
векторное равенство может быть записано в проекциях на координатные оси:
| FxΔt = Δpx; FyΔt = Δpy; FzΔt = Δpz. |
Таким образом, изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось. Рассмотрим в качестве примера одномерное движение, то есть движение тела по одной из координатных осей (например, оси OY). Пусть тело свободно падает с начальной скоростью v0 под действием силы тяжести; время падения равно t. Направим ось OY вертикально вниз. Импульс силы тяжести Fт = mg за время t равен mgt. Этот импульс равен изменению импульса тела
| Fтt = mgt = Δp = m(v – v0), откуда v = v0 + gt. |
Этот простой результат совпадает с кинематической формулой для скорости равноускоренного движения. В этом примере сила оставалась неизменной по модулю на всем интервале времени t. Если сила изменяется по величине, то в выражение для импульса силы нужно подставлять среднее значение силы Fср на промежутке времени ее действия. Рис. 1 иллюстрирует метод определения импульса силы, зависящей от времени.
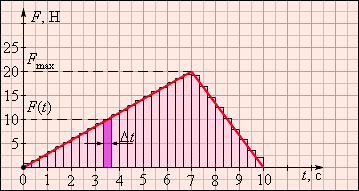 |
| Рисунок 1. Вычисление импульса силы по графику зависимости F(t). |
Выберем на оси времени малый интервал Δt, в течение которого сила F(t) практически остается неизменной. Импульс силы F(t)Δt за время Δt будет равен площади заштрихованного столбика. Если всю ось времени на интервале от 0 до t разбить на малые интервалы Δti, а затем просуммировать импульсы силы на всех интервалах Δti, то суммарный импульс силы окажется равным площади, которую образует ступенчатая кривая с осью времени. В пределе (Δti → 0) эта площадь равна площади, ограниченной графиком F(t) и осью t. Этот метод определения импульса силы по графику F(t) является общим и применим для любых законов изменения силы со временем. Математически задача сводится к интегрированию функции F(t) на интервале [0; t]. Импульс силы, график которой представлен на рис. 1, на интервале от t1 = 0 с до t2 = 10 с равен:
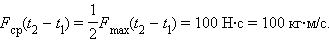 |
В этом простом примере 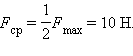 В некоторых случаях среднюю силу Fср
можно определить, если известно время ее действия и сообщенный телу импульс.
Например, сильный удар футболиста по мячу массой 0,415 кг может сообщить
ему скорость v = 30 м/с. Время удара приблизительно равно
8·10–3 с. Импульс p, приобретенный мячом в результате удара есть:
В некоторых случаях среднюю силу Fср
можно определить, если известно время ее действия и сообщенный телу импульс.
Например, сильный удар футболиста по мячу массой 0,415 кг может сообщить
ему скорость v = 30 м/с. Время удара приблизительно равно
8·10–3 с. Импульс p, приобретенный мячом в результате удара есть:
| p = mv = 12,5 кг·м/с. |
Следовательно, средняя сила Fср, с которой нога футболиста действовала на мяч во время удара, есть:
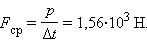 |
Это очень большая сила. Она приблизительно равна весу тела массой
160 кг. Если движение тела во время действия силы происходило по некоторой
криволинейной траектории, то начальный 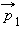 и конечный
и конечный 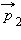 импульсы тела могут отличаться не
только по модулю, но и по направлению. В этом случае для определения изменения
импульса
импульсы тела могут отличаться не
только по модулю, но и по направлению. В этом случае для определения изменения
импульса 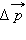 удобно использовать диаграмму импульсов, на которой изображаются вектора
удобно использовать диаграмму импульсов, на которой изображаются вектора
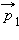 и
и 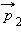 , а также вектор
, а также вектор
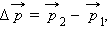 построенный
по правилу параллелограмма. В качестве примера на рис. 2 изображена
диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой m
налетел на стенку со скоростью
построенный
по правилу параллелограмма. В качестве примера на рис. 2 изображена
диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой m
налетел на стенку со скоростью 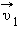 под углом α к нормали (ось OX) и
отскочил от нее со скоростью
под углом α к нормали (ось OX) и
отскочил от нее со скоростью 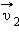 под углом β. Во время контакта со
стеной на мяч действовала некоторая сила
под углом β. Во время контакта со
стеной на мяч действовала некоторая сила 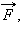 направление которой совпадает с
направлением вектора
направление которой совпадает с
направлением вектора 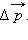
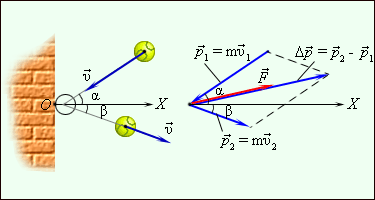 |
| Рисунок 2. Отскок мяча от шероховатой стенки и диаграмма импульсов. |
При нормальном падении мяча массой m на упругую стенку со скоростью 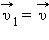 после отскока
мяч будет иметь скорость
после отскока
мяч будет иметь скорость 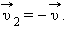 Следовательно, изменение импульса мяча за время отскока равно
Следовательно, изменение импульса мяча за время отскока равно 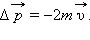 В проекциях на
ось OX этот результат можно записать в скалярной форме Δpx = –2mvx.
Ось OX направлена от стенки (как на рис. 2), поэтому
vx < 0 и Δpx > 0. Следовательно, модуль Δp изменения
импульса связан с модулем v скорости мяча соотношением Δp = 2mv.
В проекциях на
ось OX этот результат можно записать в скалярной форме Δpx = –2mvx.
Ось OX направлена от стенки (как на рис. 2), поэтому
vx < 0 и Δpx > 0. Следовательно, модуль Δp изменения
импульса связан с модулем v скорости мяча соотношением Δp = 2mv.
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|