УМОВ Николай Алексеевич
ЗАКОНЫ КОЛЕБАНИИ В НЕОГРАНИЧЕННОЙ СРЕДЕ ПОСТОЯННОЙ УПРУГОСТИ
Впервые напечатано в Математическом сборнике, т. 5, 1870 г. (Прим. ред.)
§ 2. Приложим приведённые выражения к случаю волны, распространяющейся в среде постоянной упругости. Её поступательное движение совершается с постоянной скоростью, следовательно, если представим себе два бесконечно близких положения волны, то отрезки нормалей
ds, заключающиеся между ними, будут величинами, постоянными для всех точек волновой поверхности. Итак,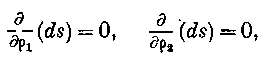
Или обращаясь к уравнению (1)
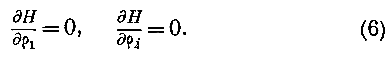
Это основные уравнения в нашем исследовании.
С их помощью ур-ния (2) дают
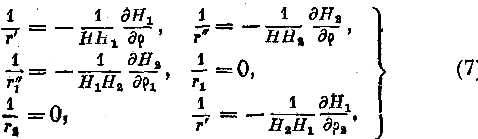
Кривизна 1/p дуги s будет по уравнениям (3) и (7)
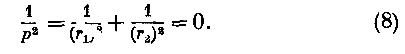
Этот результат известен: линия
s, пересечение поверхностей μ1 и μ2, есть прямая, нормальная к поверхностям (”; эта нормаль имеет здесь значение луча.Отсюда вытекает естественный выбор параметра р. Он может представлять отрезок луча между некоторым начальным и настоящим положением волны.
При таком выборе
ds = d\> и по уравнению (1) имеем Я = 1.Итак, мы имеем теорему:
Если принимаем за параметр волны отрезок луча между начальным и последующим положением волны, то её дифференциальный параметр первого порядка есть во всём пространстве величина постоянная и равная 1.
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|