Рис.26. Схема движения индексов при сортировке вставкой.
При работе со списками очень часто возникает необходимость перестановки элементов списка в определенном порядке. Такая задача называется сортировкой списка и для ее решения существуют различные методы. Рассмотрим некоторые из них.
Задача сортировки заключается в следующем: задан список целых чисел (простейший случай) В=< K1, K2,..., Kn >. Требуется переставить элементы списка В так, чтобы получить упорядоченный список B'=< K'1, K'2,...,K'n >, в котором для любого 1<=i<=n элемент K'(i) <= K'(i+1).
При обменной сортировке упорядоченный список В' получается из В систематическим обменом пары рядом стоящих элементов, не отвечающих требуемому порядку, пока такие пары существуют.
Наиболее простой метод систематического обмена соседних элементов с неправильным порядком при просмотре всего списка слева на право определяет пузырьковую сортировку: максимальные элементы как бы всплывают в конце списка.
Пример:
B=<20,-5,10,8,7>, исходный список;
B1=<-5,10,8,7,20>, первый просмотр;
B2=<-5,8,7,10,20>, второй просмотр;
B3=<-5,7,8,10,20>, третий просмотр.
В последующих примерах будем считать, что сортируется одномерный массив (либо его часть от индекса n до индекса m) в порядке возрастания элементов.
Нижеприведенная функция bubble сортирует входной массив методом пузырьковой сортировки.
/* сортировка пузырьковым методом */
float * bubble(float * a, int m, int n)
{
char is=1;
int i;
float c;
while(is)
{ is=0;
for (i=m+1; i<=n; i++)
if ( a[i] < a[i-1] )
{ c=a[i];
a[i]=a[i-1];
a[i-1]=c;
is=1;
}
}
return(a);
}
Пузырьковая сортировка выполняется при количестве действий Q=(n-m)*(n-m) и не требует дополнительной памяти.
Упорядоченный массив B' получается из В следующим образом: сначала он состоит из единственного элемента К1; далее для i=2,...,N выполняется вставка узла Кi в B' так, что B' остается упорядоченным списком длины i.
Например, для начального списка B=< 20,-5,10,8,7 > имеем:
B=< 20,-5,10,8,7> B'=< >
B=< -5,10,8,7 > B'=< 20 >
B=< 10,8,7 > B'=< -5,20 >
B=< 8,7 > B'=< -5,10,20 >
B=< 7 > B'=< -5,8,10,20 >
B=< > B'=< -5,7,8,10,20 >
Функция insert реализует сортировку вставкой.
/* сортировка методом вставки */
float *insert(float *s, int m, int n)
{
int i,j,k;
float aux;
for (i=m+1; i<=n; i++)
{ aux=s[i];
for (k=m; k<=i && s[k]=k; j--) s[j+1]=s[j];
s[k]=aux;
}
return(a);
}
Здесь оба списка В и В' размещаются в массиве s, причем список В занимает часть s c индексами от i до n, а B' - часть s c индексами от m до i-1 (см. рис.26).
При сортировке вставкой требуется Q=(n-m)*(n-m) сравнений и не требуется дополнительной памяти.
Рис.26. Схема движения индексов при сортировке вставкой.
Упорядоченный список В' получается из В многократным применением выборки из В минимального элемента, удалением этого элемента из В и добавлением его в конец списка В', который первоначально должен быть пустым.
Например:
B=<20,10,8,-5,7>, B'=< >
B=<20,10,8,7>, B'=<-5>
B=<20,10,8>, B'=<-5,7>
B=<20,10>, B'=<-5,7,8>
B=<20>, B'=<-5,7,8,10>
B=< >, B'=<-5,7,8,10,20> .
Функция select упорядочивает массив s сортировкой посредством выбора.
/* сортировка методом выбора */
double *select( double *s, int m, int n)
{
int i,j;
double c;
for (i=m; is[j])
{ c=s[i];
s[i]=s[j];
s[j]=c;
}
return(s);
}
Здесь, как и в предыдущем примере оба списка В и В' размещаются в разных частях массива s (см. рис.27). При сортировке посредством выбора требуется Q=(n-m)*(n-m) действий и не требуется дополнительной памяти.
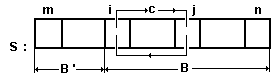Рис.27. Схема движения индексов при сортировке выбором.
Сортировка квадратичной выборкой. Исходный список В из N элементов делится
на М подсписков В1,В2,...,Вm, где М равно квадратному корню из N, и в каждом В1
находится минимальный элемент G1. Наименьший элемент всего списка В
определяется как минимальный элемент Gj в списке Упорядоченные списки А и В длин М и N сливаются в один упорядоченный список
С длины М+N, если каждый элемент из А и В входит в С точно один раз. Так,
слияние списков А=<6,17,23,39,47> и В=<19,25,38,60> из 5 и 4 элементов дает в
качестве результата список С=<6,17,19,23,25,38,39,47,60> из 9 элементов.
Для слияния списков А и В список С сначала полагается пустым, а затем к нему
последовательно приписывается первый узел из А или В, оказавшийся меньшим и
отсутствующий в С.
Составим функцию для слияния двух упорядоченных, расположенных рядом частей
массива s. Параметром этой функции будет исходный массив s с выделенными в нем
двумя расположенными рядом упорядоченными подмассивами: первый с индекса low до
индекса low+l, второй с индекса low+l+1 до индекса up, где переменные low, l,
up указывают месторасположения подмассивов. Функция merge осуществляет слияние
этих подмассивов, образуя на их месте упорядоченный массив с индексами от low до
up (см. рис.28).
Для получения упорядоченного списка B' последовательность значений
В=<K1,K2,...,Kn> разделяют на N списков В1=<K1>, B2=<K2>,...,Bn=<Kn>, длина
каждого из которых 1. Затем осуществляется функция прохода, при которой М>=2
упорядоченных списков B1,B2,...,Bm заменяется на М/2 (или (М+1)/2)
упорядоченных списков, B(2i-1)-oго и B(2i)-ого ( 2i<=M ) и добавлением Вm при
нечетном М. Проход повторяется до тех пор пока не получится одна
последовательность длины N.
Приведем пример сортировки списка путем использования слияния, отделяя
последовательности косой чертой, а элементы запятой.
Пример:
Количество действий, требуемое для сортировки слиянием, равно Q=N*log2(N),
так как за один проход выполняется N сравнений, а всего необходимо осуществить
log2(N) проходов. Сортировка слиянием является очень эффективной и часто
применяется для больших N, даже при использовании внешней памяти.
Функция smerge упорядочивает массив s сортировкой слиянием, используя
описанную ранее функцию merge.
Для сортировки массива путем слияния удобно использовать рекурсию. Составим
рекурсивную функцию srecmg для сортировки массива либо его части. При каждом
вызове сортируемый массив делится на две равных части, каждая из которых
сортируется отдельно, а затем происходит их слияние, как это показано на рис.29.
Быстрая сортировка состоит в том, что список В=< K1,K2,...,Kn>
реорганизуется в список B',< K1 >,B", где В' - подсписок В с элементами, не
большими К1, а В" - подсписок В с элементами, большими К1. В списке
B',< K1 >,B" элемент К1 расположен на месте, на котором он должен быть в
результирующем отсортированном списке. Далее к спискам B' и В" снова
применяется упорядочивание быстрой сортировкой. Приведем в качестве примера
сортировку списка, отделяя упорядоченные элементы косой чертой, а элементы Ki
знаками < и >.
Пример:
Время работы по сортировке списка методом быстрой сортировки зависит от
упорядоченности списка. Оно будет минимальным, если на каждом шаге разбиения
получаются подсписки B' и В" приблизительно равной длины, и тогда требуется
около N*log2(N) шагов. Если список близок к упорядоченному, то требуется около
(N*N)/2 шагов.
Рекурсивная функция quick упорядочивает участок массива s быстрой
сортировкой.
Здесь используются два индекса i и j, проходящие части массива навстречу
друг другу (см. рис.30). При этом i всегда фиксирует разделяющий элемент
cnt=s[low], слева от которого находятся числа, не большие cnt, а справа от i
- числа, большие cnt. Возможны три случая: при s[i+1]<=cnt; при s[i+1]>cnt и
s[j]<=cnt; при s[i+1]>cnt и s[j]>cnt. По окончании работы i=j, и cnt=s[i]
устанавливается на своем месте.
Быстрая сортировка требует дополнительной памяти порядка log2(N) для
выполнения рекурсивной функции quick (неявный стек).
Оценка среднего количества действий, необходимых для выполнения быстрой
сортировки списка из N различных чисел, получена как оценка отношения числа
различных возможных последовательностей из N различных чисел, равного N!, и
общего количества действий C(N), необходимых для выполнения быстрой сортировки
всех различных последовательностей. Доказано, что C(N)/N! < 2*N*ln(N).
Распределяющая сортировка. Предположим, что элементы линейного списка В есть
Т-разрядные положительные десятичные числа D(j,n) - j-я справа цифра в
десятичном числе n>=0, т.е. D(j,n)=floor(n/m)%10, где m=10^(j-1). Пусть
В0,В1,...,В9 - вспомогательные списки (карманы), вначале пустые.
Для реализации распределяющей сортировки выполняется процедура, состоящая из
двух процессов, называемых распределение и сборка для j=1,2,...,T.
PАСПРЕДЕЛЕНИЕ заключается в том, что элемент Кi (i=1,N) из В добавляется как
последний в список Bm, где m=D(j,Ki), и таким образом получаем десять списков,
в каждом из которых j-тые разряды чисел одинаковы и равны m.
СБОРКА объединяет списки В0,В1,...,В9 в этом же порядке, образуя один список
В.
Рассмотрим реализацию распределяющей сортировки при Т=2 для списка:
B=<09,07,18,03,52,04,06,08,05,13,42,30,35,26> .
Количество действий, необходимых для сортировки N T-цифровых чисел,
определяется как Q(N*T). Недостатком этого метода является необходимость
использования дополнительной памяти под карманы.
Однако можно исходный список представить как связанный и сортировку
организовать так, чтобы для карманов В0,В1,...,В9 не использовать дополнительной
памяти, элементы списка не перемещать, а с помощью перестановки указателей
присоединять их к тому или иному карману.
В представленной ниже программе функция pocket реализует распределяющую
сортировку связанного линейного списка (указатель q), в котором содержатся
Т-разрядные десятичные положительные числа, без использования дополнительной
памяти; в функции a[i], b[i] указывают соответственно на первый и на последний
элементы кармана Bi.
На рис.31 показана схема включения очередного элемента списка в К-й карман.
Разновидностью распределяющей сортировки является битовая сортировка. В ней
элементы списка интерпретируются как двоичные числа, и D(j,n) обозначает j-ю
справа двоичную цифру числа n. При этой сортировке в процессе РАСПРЕДЕЛЕНИЕ
требуются только два вспомогательных кармана В0 и В1; их можно разместить в
одном массиве, двигая списки В0 и В1 навстречу друг другу и отмечая точку
встречи. Для осуществления СБОРКИ нужно за списком В0 написать инвертированный
список В1.
Так как выделение j-го бита требует только операций сдвига, то битовая
сортировка хорошо подходит для внешней сортировки на магнитных лентах и дисках.
Разновидностью битовой сортировки является бинарная сортировка. Здесь из
всех элементов списка B=2.2.4. Слияние списков
/* слияние списков */
double *merge(double *s, int low, int up, int l)
{
double *b,*c,v;
int i,j,k;
b=calloc(l,sizeof(double));
c=calloc(up+1-l,sizeof(double));
for(i=low;i<low+l;i++)
b[i-low]=s[i];
for(i=0;i<up-l;i++)
c[i]=s[i+l+low];
v=(b[l]=(c[up-l]=(s[low+l-1]>s[up-1]) ?
(s[low+l-1]+1) : (s[up-1]+1)));
i=(j=0);
k=low;
while(b[i]<v||c[j]<v)
{ if(b[i]<c[j]) s[k]=b[i++];
else s[k]=c[j++];
k++;
}
return (s);
}
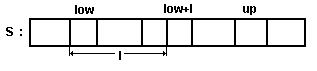Рис.28. Схема движения индексов при слиянии списков.2.2.5. Сортировка списков путем слияния
9 / 7 / 18 / 3 / 52 / 4 / 6 / 8 / 5 / 13 / 42 / 30 / 35 / 26;
7,9 / 3,18 / 4 / 52 / 6 / 8 / 54 / 13 / 30 / 42 / 26 / 35;
3,7,9,18 / 4,6,8,52 / 5,13,30,42 / 26,35;
3,4,6,7,8,9,18,52 / 5,13,26,30,35,42;
3,4,5,6,7,8,9,13,18,26,30,35,42,52.
/* сортировка слиянием */
double *smerge (double *s, int m, int n)
{ int l,low,up;
double *merge (double *, int, int, int);
l=1;
while(l<=(n-m))
{ low=m;
up=m-1;
while (l+up < n)
{ up=(low+2*l-1 < n) ? (low+2*l-1) : n ;
merge (s,low,up,l);
low=up-1;
}
l*=2;
}
return(a);
}
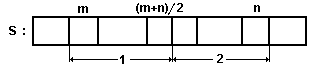Рис.29. Схема сортировки слиянием.
/* рекурсивная сортировка слиянием 1/2 */
double *srecmg (double *a, int m, int n)
{ double * merge (double *, int, int, int);
double * smerge (double *, int, int);
int i;
if (n>m)
{ i=(n+m)/2;
srecmg(a,m,i);
srecmg(a,i+1,n);
merge(a,m,n,(n-m)/2+1);
}
return (a);
}
2.2.6. Быстрая и распределяющая сортировки
9, 7, 18, 3, 52, 4, 6, 8, 5, 13, 42, 30, 35, 26
7, 3, 4, 6, 8, 5/ <9>/ 18, 52, 13, 42, 30, 35, 26
3, 4, 6, 5/<7>/ 8/ 9/ 13/ <18>/ 52, 42, 30, 35, 26
<3>/ 4, 6, 5/ 7/ 8/ 9/ 13/ 18/ 42, 30, 35, 26/ <52>
3/ <4>/ 6, 5/ 7/ 8/ 9/ 13/ 18/ 30, 35, 26/ <42>/ 52
3/ 4/ 5/ <6>/ 7/ 8/ 9/ 13/ 18/ 26/ <30>/ 35/ 42/ 52
/* быстрая сортировка */
double * quick(double *s,int low,int hi)
{ double cnt,aux;
int i,j;
if (hi>low)
{ i=low;
j=hi;
cnt=s[i];
while(i < j)
{ if (s[i+1]<=cnt)
{ s[i]=s[i+1];
s[i+1]=cnt;
i++;
}
else
{ if (s[j]<=cnt)
{ aux=s[j];
s[j]=s[i+1];
s[i+1]=aux;
}
j--;
}
}
quick(s,low,i-1);
quick(s,i+1,hi);
}
return(s);
}
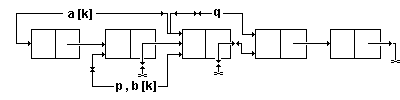Рис.30. Схема быстрой сортировки.
РАСПРЕДЕЛЕНИЕ-1:
B0=<30>, B1=< >, B2=<52,42>, B3=<03,13>, B4=<04>,
B5=<05,35>, B6=<06,26>,B7=<07>, B8=<18,08>, B9=<09>.
СБОРКА-1:
B=<30,52,42,03,13,04,05,35,06,26,07,18,08,09>
РАСПРЕДЕЛЕНИЕ-2:
B0=<03,04,05,06,07,08,09>, B1=<13,18>, B2=<26>,
B3=<30,35>, B4=<42>, B5=<52>, B6=< >,B7=< >,B8=< >, B9=< >.
СБОРКА-2:
B=<03,04,05,06,07,08,09,13,18,26,30,35,42,52>.
/* вызов распределяющeй сортировки списка */
#include
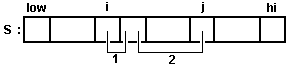Рис.31. Схема включения очередного элемента списка в карман.
Знаете ли Вы, что любой разумный человек скажет, что не может быть улыбки без кота и дыма без огня, что-то там, в космосе, должно быть, теплое, излучающее ЭМ-волны, соответствующее температуре 2.7ºК. Действительно, наблюдаемое космическое микроволновое излучение (CMB) есть тепловое излучение частиц эфира, имеющих температуру 2.7ºK. Еще в начале ХХ века великие химики и физики Д. И. Менделеев и Вальтер Нернст предсказали, что такое излучение (температура) должно обнаруживаться в космосе. В 1933 году проф. Эрих Регенер из Штуттгарта с помощью стратосферных зондов измерил эту температуру. Его измерения дали 2.8ºK - практически точное современное значение. Подробнее читайте в FAQ по эфирной физике.
