 Рис.31. Задача о Ханойских башнях.
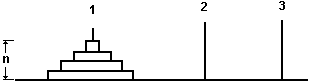
Рис.31. Задача о Ханойских башнях.
Функция называется рекурсивной, если во время ее обработки возникает ее повторный вызов, либо непосредственно, либо косвенно, путем цепочки вызовов других функций.
Прямой (непосредственной) рекурсией является вызов функции внутри тела этой функции.
int a()
{.....a().....}
Косвенной рекурсией является рекурсия, осуществляющая рекурсивный вызов функции посредством цепочки вызова других функций. Все функции, входящие в цепочку, тоже считаются рекурсивными.
Например:
a(){.....b().....}
b(){.....c().....}
c(){.....a().....} .
Все функции a,b,c являются рекурсивными, так как при вызове одной из них, осуществляется вызов других и самой себя.
Рассмотрим задачу о Ханойских башнях. Имеются три стержня с номерами 1,2,3. На стержень 1 надето n дисков различного диаметра так, что они образуют пирамиду (см.рис.31). Написать программу для печати последовательности перемещений дисков со стержня на стержень, необходимых для переноса пирамиды со стержня 1 на стержень 3 при использовании стержня 2 в качестве вспомогательного. При этом за одно перемещение должен переноситься только один диск, и диск большего диаметра не должен помещаться на диск меньшего диаметра. Доказано, что для n дисков минимальное число необходимых перемещений равно 2^n-1.
 Рис.31. Задача о Ханойских башнях.
Рис.31. Задача о Ханойских башнях.
Для решения простейшего случая задачи, когда пирамида состоит только из одного диска, необходимо выполнить одно действие - перенести диск со стержня i на стержень j, что очевидно (этот перенос обозначается i -> j). Общий случай задачи изображен на рисунке, когда требуется перенести n дисков со стержня i на стержень j, считая стержень w вспомогательным. Сначала следует перенести n-1 диск со стержня i на стержень w при вспомогательном стержне j, затем перенести один диск со стержня i на стержень j и, наконец, перенести n-1 диск из w на стержень j, используя вспомогательный стержень i. Итак, задача о переносе n дисков сводится к двум задачам о переносе n-1 диска и одной простейшей задаче. Схематически это можно записать так: T(n,i,j,w) = T(n-1,i,w,j), T(1,i,j,w), T(n-1,w,j,i).
i n-1 w n-1 j
+ | -------->-+|+--------->+ |
n-1| | I ||| Ш | |
+ / \ / \ / \
+-/-----\-+ / \ +-/-----\-+
==+----|----+===/=========\====+----|----+======
+-------------->-------------+
П
Рис.32. Схема решения задачи о Ханойских башнях.
Ниже приведена программа, которая вводит число n и печатает список перемещений, решающая задачу о Ханойских башнях при количестве дисков n. Используется внутренняя рекурсивная процедура tn(n,i,j,w), печатающая перемещения, необходимые для переноса n дисков со стержня i на стержень j с использованием вспомогательного стержня w при {i,j,w} = {1,3,2}.
/* ханойские башни */ #includemain() /* вызывающая */ { void tn(int, int, int, int); /* функция */ int n; scanf(" %d",&n); tn(n,1,2,3); } void tn(int n, int i, int j, int w) /* рекурсивная */ { if (n>1) /* функция */ { tn (n-1,i,w,j); tn (1,i,j,w); tn (n-1,w,j,i); } else printf(" \n %d -> %d",i,j); return ; }
Последовательность вызовов процедуры tn при m=3 иллюстрируется древовидной структурой на рис.33. Каждый раз при вызове процедуры tn под параметры n, i, j, w выделяется память и запоминается место возврата. При возврате из процедуры tn память, выделенная под параметры n, i, j, w, освобождается и становится доступной память, выделенная под параметры n, i, j, w предыдущим вызовом, а управление передается в место возврата.
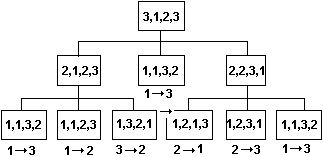 Рис.33. Последовательность вызовов процедуры tn.
Рис.33. Последовательность вызовов процедуры tn.
Во многих случаях рекурсивные функции можно заменить на эквивалентные нерекурсивные функции или фрагменты, используя стеки для хранения точек вызова и вспомогательных переменных.
Предположим, что имеется ситуация:
main() /* вызывающая функция */
{ ... f() ...}
f() /* рекурсивная функция */
{ ... f() ...}
Здесь в функции main вызывается рекурсивная функция f. Требуется заменить описание функции f и ее вызова на эквивалентный фрагмент программы, т.е. удалить функцию f.
Пусть рекурсивная функция f имеет параметры Р1,Р2,...,Рs, внутренние переменные V1,V2,...,Vt и в функциях main и f имеется k обращений к функции f. Для удаления такой функции требуются следующие дополнительные объекты:
- переменные AR1,AR2,...,ARs, содержащие значения фактических параметров при вызове функции f (типы переменных должны соответствовать типам параметров Р1,Р2,...,Рs);
- переменная rz для вычисляемого функцией f результата (тип переменных совпадает с типом возвращаемого значения функции f);
- стек, содержащий в себе все параметры и все внутренние переменные функции f, а также переменную lr типа int, для хранения точки возврата, и переменную pst типа указатель, для хранения адреса предыдущего элемента стека;
- указатель dl для хранения адреса вершин стека;
- промежуточный указатель u для операций над стеком;
- k новых меток L1,...,Lk для обозначенных точек возврата;
- метка jf, используемая для обхода модифицированного тела функции f;
- промежуточная переменная l типа int для передачи номера точки возврата.
Чтобы получить эквивалентную нерекурсивную программу без функции f, необходимо выполнить следующие действия:
1. Убрать объявление функции f в функцию main;
2. Добавить в функции main объявления переменных AR1,AR2,...,ARs,RZ, объявления стека ST и указателей dl и u:
typedef struct st { P1;P2;...;Ps;V1;V2;...;Vt;
int lr; struct st *pst } ST;
ST *dl=NULL, *u;
3. Модифицировать тело функции f во фрагмент программы. Для этого следует:
а) удалить заголовок функции f;
б) объявления параметров и внутренних переменных и заменить фрагментом:
goto jf;
f: a=malloc(sizeof(ST));
a->P1=AR1; a->P2=AR2; ... ;a->Ps=ARs;
a->lr=l; a->pst=dl; dl=a;
в) в конце функции f поставить метку JF, а все обращения к формальным аргументам заменить обращением, к соответствующим элементам стека;
г) вместо каждого оператора return(y) в функции f записать фрагмент:
RZ=y; l=dl->lr;
a=dl; dl=a->pst; free(a);
switch(l)
{ case 1: goto L1;
case 2: goto L2;
...
case k: goto Lk;
}
4. Каждый i-тый вызов функции f (как в вызывающей функции, так и в теле функции f) вида V=f(A1,A2,...,As) заменить фрагментом программы :
AR1=A1; AR2=A2; ... ; ARs=As; l=i; goto f;
Li: V=RZ;
где l=i обозначает l=1 при первом обращении к функции f, l=2 при втором обращении и т.д. Нумерация обращений может быть выполнена в произвольном порядке и требуется для возвращения в точку вызова с помощью операторов switch и goto Li; (где Li есть L1 при первой замене, Li есть L2 при второй замене и т.д.)
5. Вставить модифицированное тело функции f в конце функции main.
Для иллюстрации изложенного рассмотрим несколько вариантов реализации программы вычисляющей функцию Аккермана, которая определяется так:
+ X+1, если N=0
| X, если N=1, Y=0,
| 0, если N=2, Y=0,
A(N,X,Y)= | 1, если N=3, Y=0,
| 2, если N=>4, Y=0,
+ A(N-1,A(N,X,Y-1),X), если N#0, Y#0;
где N,X,Y - целые неотрицательные числа.
Следующая программа вычисляет функцию Аккермана с использованием рекурсивной функции ackr и вспомогательной функции smacc:
/* рекурсивное вычисление функции Аккермана */
# include
main () /* вызывающая */
{ int x,y,n,t; /* функция */
int ackr(int, int, int);
scanf("%d %d %d",&n,&x,&y);
t=ackr(n,x,y);
printf("%d",t);
}
int smacc( int n,int x ) /* вспомогательная */
{ switch (n) /* функция */
{ case 0: return(x+1);
case 1: return (x);
case 2: return (0);
case 3: return (1);
default: return (2);
}
}
int ackr( int n, int x, int y) /* рекурсивная */
{ int z; /* функция */
int smacc( int,int);
if(n==0 || y==0) z=smacc(n,x);
else { z=ackr(n,x,y-1); /* рекурсивные */
z=ackr(n-1,z,x); } /* вызовы ackr(...) */
return z;
}
Модифицируя функции main и ackr в соответствии с изложенным методом получим следующую программу:
/* Эквивалентная нерекурсивная программа */
/* для вычисления функции Аккермана */
#include
#include
int main()
{ typedef struct st
{ int i,j,k,z,lr;
struct st *pst;
} ST;
ST *u, *dl=NULL;
int l,x,y,n;
int smacc(int,int);
int an,ax,ay,rz,t;
scanf("%i %i %i",&n,&x,&y);
an=n;ax=x;ay=y;l=1; /* - замена вызова - */
goto ackr; /* t=ackr(n,x,y); */
l1: t=rz; /* - - - - - - - - */
printf("\n %d ",t);
goto jackr;
/* начало фрагмента заменяющего функцию ackr */
ackr:
u=( ST *) malloc( sizeof (ST) );
u->i=an;
u->j=ax;
u->k=ay;
u->lr=l;
u->pst=dl;
dl=u;
if (an==0||ay==0)
dl->z=smacc(an,ax);
else
{
an=dl->i; /* - замена вызова - */
ax=dl->j; /* */
ay=dl->k-1; /* z=ackr(n,x,y-1); */
l=2; /* */
goto ackr; /* */
l2: dl->z=rz; /* - - - - - - - - */
an=dl->i-1; /* - замена вызова - */
ax=rz; /* */
ay=dl->j; /* z=ackr(n-1,z,x); */
l=3; /* */
goto ackr; /* */
l3: dl->z=rz; /* - - - - - - - - */
}
rz=dl->z; /* - - - - - - - - */
an=dl->i; /* */
ax=dl->j; /* замена */
ay=dl->k; /* */
l=dl->lr; /* оператора */
u=dl; /* */
dl=u->pst; /* return z ; */
free(u); /* */
switch(l) /* */
{ case 1: goto l1; /* */
case 2: goto l2; /* */
case 3: goto l3; /* */
} /* - - - - - - - - */
jackr:
}
int smacc( int n,int x ) /* вспомогательная функция */
{ switch (n)
{ case 0: return(x+1);
case 1: return (x);
case 2: return (0);
case 3: return (1);
default: return (2);
}
}
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|