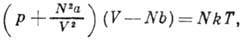
Ван-дер-Ваальса уравнение - уравнение состояния реального газа. Предложено И. Д. Ван-дер-Ваальсом
(J. D. van der Waals) в 1873. Для газа, содержащего N молекул, В. у.
имеет вид:
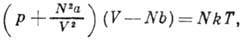
где V - объём, р - давление, T - абс. темп-pa газа, а и b - постоянные,
учитывающие притяжение и отталкивание молекул. Член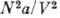 
наз. внутр. давлением, постоянная b равна учетверённому объёму молекулы
газа, если в качестве модели молекулы принять слабо притягивающиеся упругие
сферы.
В. у. количественно определяет
свойства реальных газов лишь в небольшом интервале Т и р - в области
относительно высоких Т и низких р, т. к. а и b являются
функциями температуры. Однако Ван-дер-Ваальса уравнение качественно правильно описывает поведение газа
и жидкости и при высоких р, а также особенности фазового перехода между
ними. При низких давлениях и относительно высоких темп-pax оно переходит в ур-ние
состояния идеального газа (Клапейрона уравнение ),а при высоких давлениях
и низких темп-pax учитывает малую сжимаемость жидкостей. В. у. описывает, кроме
того, критическое и ме-тастабильное состояния системы жидкость - пар.
На рис. приведены в координатах
р - V изотермы, рассчитанные по Ван-дер-Ваальса уравнению, являющемуся кубическим относительно
V. Возможны 3 случая решения Ван-дер-Ваальса уравнения: 1) все три корня действительные и
равны между собой; этот случай соответствует критич. состоянию (изотерма Ткр;
2) все три корня действительные и различные - т. н. докритич. состояние (изотермы
при T<Tкр); 3) два корня мнимые, не имеющие физ.
смысла, один корень действительный; этот случай соответствует сверхкри-тич.
состоянию (изотермы при T>Tкр). Изотермы при Т/Ткр
качественно описывают поведение реальных газов. При докритич. темп-pax Т<Ткр
поведение газа описывается изотермой-изобарой насыщенного пара - прямой на диаграмме
р - V, напр. прямой ас(рн.n.=const), а не S-образной
кривой adec, соответствующей В. у.
Геом. место начальных и
конечных точек "равновесия" а и с стабильной и метастабильной фаз
(определяемое из условия равенства заштрихованных площадей) наз. бинодалью (кривая
аКс). Кривая, соединяющая экстремальные точки типа d и е, наз.
спинодалью (кривая dKe). Область, заключённая между бинодалью и спинодалью,-
область неустойчивого, метастабиль-ного состояния системы. T. о., участки изотерм
типа ad и ес относятся к метастабильному равновесию соответственно
перегретой жидкости и системы жидкость+ газ, а также системы жидкость+газ и
переохлаждённого газа. Участок dbe не имеет физ. смысла, т. к. на этом
участке при росте р увеличивается и V, что невозможно.
При достаточно низких темп-pax
участок adb опускается ниже изобары р=0. В этом случае имеющий
физ. смысл участок
ad попадёт в область отрицат. давлений, что соответствует неустойчивому
состоянию растянутой жидкости.
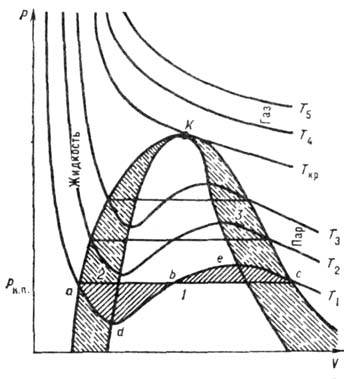
Диаграмма состояния вещества в координатах p-V: T1<T2< T3 < Tкр < T4 < Т5,-изотермы, рассчитанные по В. у.; К - критическая точка, линии аКс - бинодаль, dKe - спинодаль; 1 - область жидкость + газ; 2 и 3 - области метастабильного состояния систем: перегретая жидкость и жидкость+ пар, переохлаждённый пар и жидкость+ пар. Заштрихованные площади adb и bес равны.
С помощью В. у. можно получить
критич. параметры ркр, Vкp и Tкp.
В точке К изотермы Ван-дер-Ваальса имеют как максимум, так и точку перегиба,
т. е.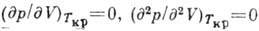 
. Решение системы ур-ний Ван-дер-Ваальса и двух приведённых выше имеет вид:
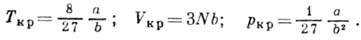
Несмотря на то, что постоянная
b имеет подгоночный характер, размеры молекул, полученные с помощью выражения
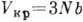, хорошо
согласуются с полученными др. методами.
В. у., в к-рое введены
относит. величины T/Ткр, р/ркр,
T/Tкр, наз. приведённым ур-нием состояния; оно имеет более
широкое применение, чем В. у. Если в В. у. давление разложить по степеням плотности
и сравнить с вириальним разложением, то постоянные а и b можно
выразить через вириальные коэффициенты.
|
|
 |
