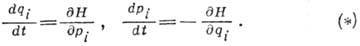
Гамильтона уравнения (канонические уравнения механики). РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Гамильтона уравнения (канонические уравнения механики) - дифференциальные ур-ния движения голономной механич. системы в канонич. переменных, к-рыми являются s обобщённых координат q_i и s обобщённых импульсов p_i, где s - число степеней свободы системы. Выведены У. P. Гамильтоном (W. R. Hamilton) в 1834. Для составления Г. у. надо в качестве характеристич. функции системы знать Гамильтона функцию Н(g_i, р_i, t), где t - время. Тогда, если все действующие на систему силы потенциальны, Г. у. имеют вид

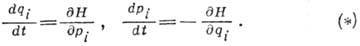
Если наряду с потенциальными на систему действуют непотенциальные силы F, то к правым частям 2-й группы ур-ний (*) надо прибавить соответствующие обобщённые силы Q_i. Ур-ния (*) представляют собой систему 2s обыкновенных дифференц. ур-ний 1-го порядка, интегрируя к-рые можно найти все q_i и p_iкак функции времени t и 2s постоянных интегрирования, определяемых по нач. данным. Решение системы ур-ний (*) можно также свести к отысканию полного интеграла соответствующего ей ур-ния в частных производных (см. Гамильтона - Якоби уравнение).

Если одна из координат q_i, напр. q₁, является циклич. координатой, т. е. явно не входит в выражение функции Н, то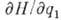

=0 и одно из ур-ний (*) даёт сразу интеграл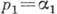

, где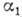

- постоянная. Особый интерес представляет случай, когда все координаты циклические, а функция

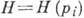явно не зависит от времени (силовое поле и наложенные связи стационарны). Тогда все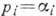

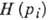, т. е. постоянны; следовательно, функции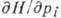

тоже постоянны, и 1-я группа ур-ний (*) даёт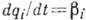

, откуда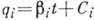

, где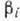

, C_i - новые постоянные. Ур-ния в этом случае интегрируются элементарно и все координаты являются линейными функциями времени. Отсюда следует, что задачу интегрирования Г. у. можно свести к задаче отыскания для системы циклич. координат. Это, в принципе, возможно, т. к. Г. у. обладают тем важным свойством, что они допускают переход с помощью т. н. канонических преобразований от переменных q_i, р_i к новым переменным Q_i(q_i, р_i, t), P_i(q_i, р_i, t), которые также являются каноническими и удовлетворяют уравнениям (*) с соответствующей функцией H(Q_i, P_i, t).

Равноправность в Г. у. координат и импульсов как независимых переменных, а также инвариантность этих ур-ний по отношению к канонич. преобразованиям открывают большие возможности для обобщений. Поэтому Г. у. имеют важные приложения не только в механике, но и во многих др. областях физики, напр. в статистич. физике, квантовой механике, электродинамике и др.

Знаете ли Вы, в чем фокус эксперимента Майкельсона?

Эксперимент А. Майкельсона, Майкельсона - Морли - действительно является цирковым фокусом, загипнотизировавшим физиков на 120 лет.

Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.

В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.

Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.