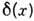Дельта-функция. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Дельта-функция,

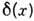1 - наиболее употребительная из обобщенных функций, определяемая формальным соотношением

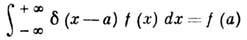
для любой непрерывной функции f(x). Введена П. Дираком (P. Dirac) в 1926. Строгое определение Д--ф. и обоснование правил действий с ней даётся теорией обобщённых функций. В этой теории Д--ф. определяется как непрерывный линейный функционал в пространстве непрерывных функций. Равенство результатов интегрирования правой и левой частей с непрерывными функциями означает справедливость соотношений:

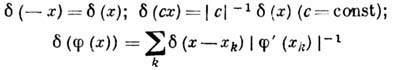
[х_k - корни ур-ния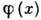

=0] и т. д. В этом же смысле определяют Д--ф. многомерного аргумента x=x₁, . . .,х_n : 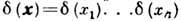. Используют также интегр. представление

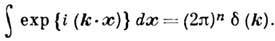
Д--ф. незаменима при матем. описании идеализиров. ситуаций, когда физ. величина (масса, заряд, интенсивность источников тепла и т. п.) сосредоточена в точке: Д--ф. задаёт распределение плотности такой величины. Напр., плотность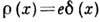

отвечает заряду е в точке х.

Д--ф. используют в совр. матем. физике при построении обобщённых и фундам. решений дифференц. ур-ний, Грина функций краевых задач, при нормировке собств. функций непрерывного спектра и т. д.

Литература по Дельта-функции

Знаете ли Вы, в чем ложность понятия "физический вакуум"?

Физический вакуум - понятие релятивистской квантовой физики, под ним там понимают низшее (основное) энергетическое состояние квантованного поля, обладающее нулевыми импульсом, моментом импульса и другими квантовыми числами. Физическим вакуумом релятивистские теоретики называют полностью лишённое вещества пространство, заполненное неизмеряемым, а значит, лишь воображаемым полем. Такое состояние по мнению релятивистов не является абсолютной пустотой, но пространством, заполненным некими фантомными (виртуальными) частицами. Релятивистская квантовая теория поля утверждает, что, в согласии с принципом неопределённости Гейзенберга, в физическом вакууме постоянно рождаются и исчезают виртуальные, то есть кажущиеся (кому кажущиеся?), частицы: происходят так называемые нулевые колебания полей. Виртуальные частицы физического вакуума, а следовательно, он сам, по определению не имеют системы отсчета, так как в противном случае нарушался бы принцип относительности Эйнштейна, на котором основывается теория относительности (то есть стала бы возможной абсолютная система измерения с отсчетом от частиц физического вакуума, что в свою очередь однозначно опровергло бы принцип относительности, на котором постороена СТО). Таким образом, физический вакуум и его частицы не есть элементы физического мира, но лишь элементы теории относительности, которые существуют не в реальном мире, но лишь в релятивистских формулах, нарушая при этом принцип причинности (возникают и исчезают беспричинно), принцип объективности (виртуальные частицы можно считать в зависимсоти от желания теоретика либо существующими, либо не существующими), принцип фактической измеримости (не наблюдаемы, не имеют своей ИСО).

Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.

Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.

Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.

Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.