Диссипативные структуры - устойчивые пространственно неоднородные структуры, возникающие в результате
развития неустойчивостей в однородной неравновесной диссипативной среде. Термин предложен И. Пригожиным (I. Prigogine). Примером Д. с. могут служить
ячейки Бенара (чередование восходящих и нисходящих конвекционных потоков в жидкости),
страты в плазме, неоднородные распределения концентраций в хим. реакторах, перистые
облака и др. явления. Основы общей теории Д. с. сформулированы А. Тьюрингом
(A. Turing) в 1952.
Простейшие модели Д. с.
описываются двумя динамич. переменными х, у, зависящими от времени t и одной пространственной координаты r:
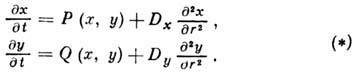
Система (*) описывает кинетику
нелинейных процессов (физ., хим., биол. и т. д.) с учётом миграции компонент
х и у (в частности, за счёт диффузии) в соседние области
пространства. Величины Dx и Dy - коэф. диффузии,
нелинейные функции P (х, у)и Q (х, у)описывают прирост и убыль
компонент х и у. Если Д. с. образуются на отрезке длины 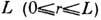 с непроницаемыми концами, граничные условия имеют вид
с непроницаемыми концами, граничные условия имеют вид 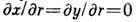 при r=0, L. Образование Д. с. возможно при след. условиях. 1)
Одна из переменных (напр., х) является "автокаталитической",
другая (у) - "демпфирующей". Это значит, что в системе, линеаризованной
вблизи стационарного состояния
при r=0, L. Образование Д. с. возможно при след. условиях. 1)
Одна из переменных (напр., х) является "автокаталитической",
другая (у) - "демпфирующей". Это значит, что в системе, линеаризованной
вблизи стационарного состояния 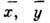 [такого, что
[такого, что 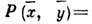
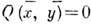 ],
величина
],
величина 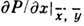 положительна,
а величина
положительна,
а величина 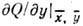 отрицательна.
Величины
отрицательна.
Величины 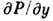 и
и 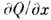 также должны иметь разные знаки. Такие условия выполняются лишь в термодинамически
неравновесных открытых системах; согласно терминологии Пригожина, они
относятся к области "нелинейной термодинамики". 2) Коэф. диффузии
автокатализатора должен быть меньше коэф. диффузии для демпфера (т. е. Dx<Dy).
также должны иметь разные знаки. Такие условия выполняются лишь в термодинамически
неравновесных открытых системах; согласно терминологии Пригожина, они
относятся к области "нелинейной термодинамики". 2) Коэф. диффузии
автокатализатора должен быть меньше коэф. диффузии для демпфера (т. е. Dx<Dy).
При выполнении условий
(1) и (2) однородное стационарное состояние 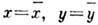 может терять устойчивость по отношению к гармонич. возмущениям с определённой
длиной волны, соизмеримой с L. Значения параметров системы (*), при к-рых
декремент затухания упомянутых возмущений обращается в нуль, наз. бифуркационными,
а само явление - бифуркацией Тьюринга. Система отбирает из внеш. возмущений
огранич. число гармонич. мод (в предельном случае одну), к-рые могут нарастать.
Их нарастание стабилизируется нелинейными членами функций P(х, у)и Q(x,
у). При значениях параметров, близких к бифуркационным, образуется плавная
гармонич. Д. с. Вдали от точки бифуркации возникают контрастные Д. с., к-рые
состоят из узких участков резкого изменения автокаталитич. переменной х, чередующихся с широкими участками плавного изменения переменных. При обратном
соотношении между коэф. диффузии
может терять устойчивость по отношению к гармонич. возмущениям с определённой
длиной волны, соизмеримой с L. Значения параметров системы (*), при к-рых
декремент затухания упомянутых возмущений обращается в нуль, наз. бифуркационными,
а само явление - бифуркацией Тьюринга. Система отбирает из внеш. возмущений
огранич. число гармонич. мод (в предельном случае одну), к-рые могут нарастать.
Их нарастание стабилизируется нелинейными членами функций P(х, у)и Q(x,
у). При значениях параметров, близких к бифуркационным, образуется плавная
гармонич. Д. с. Вдали от точки бифуркации возникают контрастные Д. с., к-рые
состоят из узких участков резкого изменения автокаталитич. переменной х, чередующихся с широкими участками плавного изменения переменных. При обратном
соотношении между коэф. диффузии 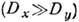 в системе возникают автоволны .Все изученные модели Д. с. разбиваются
на два класса, к-рые можно привести в соответствие с катастрофами типа "складка"
и "сборка" (см. Катастроф теория). Класс Д. с. определяется
числом экстремумов функции
в системе возникают автоволны .Все изученные модели Д. с. разбиваются
на два класса, к-рые можно привести в соответствие с катастрофами типа "складка"
и "сборка" (см. Катастроф теория). Класс Д. с. определяется
числом экстремумов функции 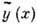 ,
являющейся решением ур-ния
,
являющейся решением ур-ния 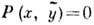 .
.
В случае одного экстремума
(складка) контрастная Д. с. состоит из ряда узких "пиков" автокаталитич.
переменной х(r), разделённых длинными участками плавного изменения обеих
переменных. Если имеется два экстремума (сборка), то возможно образование контрастных
Д. с. ступенчатой формы, состоящих из широких участков повышенного и пониженного
содержания автокатализатора; узкие границы между ними - фронты резкого изменения
х(r).
На отрезке длины L может
существовать несколько (много) разл. периодич. Д. с., реализация каждого решения
зависит от истории возникновения Д. с. Контрастные Д. с. весьма чувствительны
к малым неоднородностям пространства, поэтому могут возникать достаточно стабильные
непериодич. Д. с. (в к-рых длины плавных участков различны). Теорию Д. с. используют
для качественного описания явлений самоорганизации в природе. В частности, в
биофизике её применяют для описания спонтанного возникновения структуры
при развитии организма (морфогенез), пространственно неоднородного распределения
особей в экологии и структуры колоний у ряда микроорганизмов. Теория Д. с. входит
как существ. часть в синергетику и теорию автоволн.

Д. С. Чернавский
|
|