Изгибная деформация. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Изгибная деформация - вид деформации, характеризующийся изменением кривизны оси (бруса, балки, стержня) или срединной поверхности (пластинки, оболочки)под действием внеш. сил или температуры. Применительно к прямому брусу различают плоский (прямой), косой, чистый, поперечный и продольный И. Плоский И. возникает, когда силы, изгибающие брус, совпадают с одной из его гл. плоскостей, т. е. плоскостей, проходящих через ось бруса и гл. оси инерции его поперечных сечений. Косой И. возникает, если силы, изгибающие брус, лежат в плоскости, проходящей через ось бруса, но не совпадающей ни с одной из его главных плоскостей. Чистый И. происходит под действием только пар сил (изгибающих моментов),

Рис. 1. Изгиб бруса: a - чистый; б - поперечный; в - продольный.

напр. в случае приложения к концам бруса двух равных по величине и противоположных по направлению моментов М (рис. 1, а). Поперечный И. происходит как под действием изгибающих моментов, так и поперечных сил, напр., в случае действия на брус сосредоточенных сил (рис. 1, б). Продольный И. возникает под действием на стержень продольных сжимающих сил F (рис. 1, в), при достижении к-рыми нек-рых величин (критических сил)может произойти потеря устойчивости равновесия (см. Продольный изгиб, Устойчивость упругих систем). Изучение И. производится в предположении, что поперечные сечения бруса, плоские до И., остаются плоскими и после него (гипотеза плоских сечений), что продольные волокна бруса при И. не сжимают друг друга и не стремятся оторваться одно от другого. Получаемые при этом расчётные ф-лы применимы, если поперечные размеры бруса малы по сравнению с его длиной и отсутствуют резкие изменения поперечных сечений бруса. При чистом И. в сечениях бруса действуют только изгибающие моменты и притом постоянной величины, поэтому, если из прямого бруса, работающего в упругой области (рис. 2, а), выделить двумя поперечными сечениями элемент длиной ds, то действие отброшенных частей бруса на элемент ds можно заменить равными моментами М.

Рис. 2.а- брус, работающий в условиях чистого изгиба; б - элемент бруса ds после деформации; в - сечение бруса; г - эпюра .

При И. поперечные сечения, расположенные по концам элемента ds, наклоняются одно к другому, оставаясь плоскими (рис. 2, б), а продольные волокна, расположенные на выпуклой стороне элемента, удлиняются, на вогнутой - укорачиваются; промежуточный слой, волокна к-рого не изменяют своей длины, наз. нейтральным слоем. Линия пересечения нейтрального слоя с плоскостью любого поперечного сечения наз. нейтральной линией. При И. прямого бруса нейтральный слой проходит через центры тяжести поперечных сечений и наз. нейтральной осью (линия О-О на рис. 2, в). В сечении по одну сторону от нейтральной оси возникают растягивающие, а по другую - сжимающие нормальные напряжения s, возрастающие по мере удаления от нейтральной оси по линейному закону (рис. 2, г)s=Му/I, где y - расстояние от нейтральной оси до рассматриваемого волокна поперечного сечения, а I - момент инерции поперечного сечения относительно нейтральной оси. Для балок из материалов, одинаково работающих на растяжение и сжатие, в поперечных сечениях, симметричных относительно нейтральной оси, наибольшие нормальные напряжения в крайних волокнах определяются по ф-ле: s=bM/W, где W=2I/h - момент сопротивления поперечного сечения, h/2 - половина высоты сечения. При поперечном И. в сечениях бруса действуют как изгибающий момент, так и поперечная сила, к-рые в зависимости от вида нагрузок изменяются по длине бруса. Характер их изменения изображается графически с помощью эпюр изгибающих моментов М и поперечных сил Q (рис. 3). В поперечных сечениях кроме нормальных напряжений а возникают также касательные напряжения т. Нормальные напряжения определяются теми же ф-лами, как и при чистом И. Касательные напряжения т для заданной точки бруса (рис. 4) получаются равными в площадках, расположенных в плоскости поперечного сечения, и в площадках, параллельных нейтральному слою: по ширине сечения касательные напряжения принимаются одинаковыми и определяются ф-лой Журавского: t=QS/Ib, где Q - поперечная сила в сечении, S - статич. момент относительно нейтральной оси той части сечения, к-рая лежит выше (или ниже) рассматриваемой точки, ">b - ширина сечения на уровне этой точки. Наибольшие t имеют место у нейтральной оси бруса.

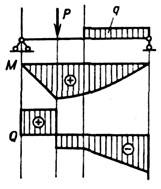
Рис. 3. Эпюры М и Q для балки, нагруженной одним сосредоточенным грузом Р и равномерно распределённой нагрузкой интенсивностью q.

При И. ось бруса искривляется, её кривизна определяется выражением 1/r=M/EI, где r -радиус кривизны изогнутой оси в рассматриваемом сечении, Е - модуль продольной упругости материала (модуль Юнга). Ордината v изогнутой оси наз. прогибом в данной точке. При малых прогибах первоначально прямых брусьев зависимость между прогибом и изгибающим моментом выражается ур-нием: d²v/dx²=M/EI, интегрированием к-рого находят выражение для изогнутой оси бруса v=f(x).

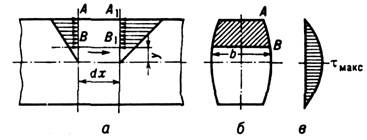
Рис. 4. Касательные напряжения при поперечном изгибе бруса: а - элемент ABB₁A₁, вырезаемый из бруса при исследовании касательных напряжений; б - сечение бруса; в - эпюра касательных напряжений.

Косой И. сводится к сочетанию двух плоских И., к-рые получаются разложением внешних сил (или изгибающих моментов) на составляющие по гл. осям инерции сечения. Нормальные напряжения обоих плоских И. складываются алгебраически и для произвольной точки сечения выражаются ф-лой:

где М_х, M_y - изгибающие моменты в сечении относительно гл. осей х и у; I_x, 1_у - моменты инерции сечения относительно гл. осей; х, у - координаты той точки поперечного сечения, в к-рой определяется напряжение. В кривых брусьях большой кривизны, у к-рых отношение радиуса кривизны r к высоте сечения h меньше 4-6, наличие кривизны резко сказывается на распределении напряжений. При чистом И. такого бруса нейтральная ось смещается от геометрич. оси к центру кривизны бруса, нормальные напряжения распределяются по высоте сечения по гиперболич. закону (рис. 5, а) и резко возрастают по мере приближения к внутр. краю бруса.

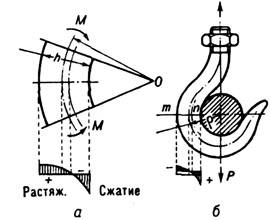
Рис. 5. Распределение напряжений: а - при чистом изгибе бруса большой кривизны; б - в крюке подъёмного приспособления.

Напр., для крюка подъёмного приспособления наибольшие напряжения возникают в сечении т - п (рис. 5, б) и складываются из двух частей: от растяжения силой Р и от И. моментом М=Рr, где Р - нагрузка на крюк, r - радиус кривизны оси бруса в области сечения т - п. Для произвольной точки сечения т - п нормальные напряжения определяются ф-лой:

где F - площадь поперечного сечения, S - статич. момент этой площади относительно нейтральной линии, у - расстояние от рассматриваемой точки до нейтральной оси, r - радиус кривизны нейтрального слоя, зависящий от формы и размеров поперечного сечения и кривизны бруса. И. бруса с учётом пластич. деформаций можно исследовать приближённо, принимая, что материал одинаково работает на растяжение и сжатие, и беря наиболее простую зависимость между напряжениями и деформациями, напр., в виде ломаной линии, состоящей из наклонного участка при упругой и горизонтального - при пластич. деформации (рис. 6). При постепенном возрастании нагрузки в сечении с наибольшим изгибающим моментом сначала возникают упругие деформации, затем в крайних точках сечения появляются пластич. области (рис. 7), к-рые, постепенно увеличиваясь, полностью охватывают обе половины сечения. Такое состояние наз. пластическим шарниром; ему соответствует предельный изгибающий момент, по которому определяют предельную нагрузку на брус.

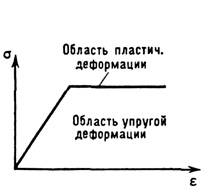
Рис. 6. Зависимость между напряжением s и деформацией e при упругопластическом изгибе бруса.

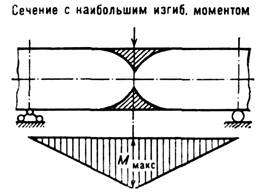
Рис. 7. Возникновение пластического шарнира в сечении с наибольшим изгибающим моментом.

При точном исследовании И. с учётом пластич. деформаций пользуются более сложными методами, изучая весь процесс деформирования бруса, его разгрузку и повторное нагружение. Исследование осложняется при необходимости учитывать влияние на И. времени, высоких температур, а также специфич. свойств материала, напр, в случае брусьев, выполняемых из пластмасс, следует учитывать реологич. эффекты (см. Реология).

Литература по изгибной деформации

Знаете ли Вы, что в 1965 году два американца Пензиас (эмигрант из Германии) и Вильсон заявили, что они открыли излучение космоса. Через несколько лет им дали Нобелевскую премию, как-будто никто не знал работ Э. Регенера, измерившего температуру космического пространства с помощью запуска болометра в стратосферу в 1933 г.? Подробнее читайте в FAQ по эфирной физике.