Реология (от греч. rheos - течение и logos - учение) - наука о деформациях и течении реальных сплошных сред (напр., неньютоновских жидкостей со структурной вязкостью ,дисперсных систем, обладающих пластичностью ).Р. рассматривает процессы, связанные с необратимыми остаточными деформациями вещества (релаксацию напряжений, последействие упругое, ползучесть материалов и т. п.). В основе Р. лежат осн. законы гидромеханики и теории упругости и пластичности (в т. ч. законы И. Ньютона о сопротивлении движению вязкой жидкости, Навье - С такса уравнения движения несжимаемой вязкой жидкости, Гука закон сопротивления упругого тела и др.).
Р. может рассматриваться как часть механики сплошных сред. В
Р. устанавливают зависимости между действующими на тело механич. напряжениями,
вызываемыми ими деформациями и их изменениями во времени. При обычных в
механике сплошных сред допущениях об однородности и сплошности материала
в теоретич. Р. решают краевые задачи деформирования и течения твёрдых и
жидких тел. Осн. внимание обращается на сложное реологич. поведение вещества
(напр., когда одновременно проявляются свойства вязкие и упругие или вязкие
и пластические). Общее реологич. ур-ние состояния вещества вряд ли может
быть установлено из-за существ. различия свойств разнообразных материалов,
но имеются ур-ния для многих частных случаев. При описании реологич. поведения
материалов пользуются механич. моделями, для к-рых составляют дифференциальные
или интегральные ур-ния, куда входят разл. комбинации упругих и вязких
характеристик. Реологич. моделями пользуются также при изучении механич.
свойств полимеров, внутреннего трения в твёрдых телах и др. свойств
реальных тел.
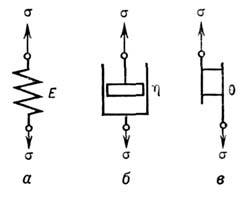
Рис. 1. Механические модели реологических сред: а - упругое тело Гука; б - вязкая жидкость Ньютона; в - шёсткопластическое тело Сен-Венана.
Для одномерных задач служат след. реологич. (механич.) модели: упругий
элемент (рис. 1,а) в виде дружины, к-рый отображает упругие свойства; жидкостный
элемент (рис. 1, б; демпфер, гидравлич. амортизатор), характеризующий вязкие
свойства материала. Действующая на упругий элемент сила моделирует напряжение
и обозначается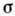
.
Деформация пружины определяет деформацию рассматриваемого реального материала
и обозначается
.
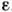Жёсткость пружины моделирует модуль упругости Е реального материала.
Связь между упругой деформацией и напряжением определяется законом Гука: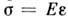
. Ньютоновская жидкость характеризуется соотношением
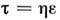(см. Ньютона закон трения),
На рис. 1, в представлена модель жёсткопластич. тела Сен-Венана,
изображаемая в виде узла сухого трения. Элементы этого узла (на рис.- вертикальные
чёрточки) смещаются один относительно другого, передавая пост. силу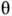
,
независимую от скорости. Если приложенное напряжение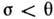
, смещения нет. Т. о., для тела Сен-Венана деформации е и скорости деформаций
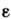равны нулю, пока напряжения а меньше предела текучести
.
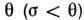При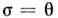
начинается
деформирование,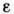
и
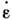при этом
становятся отличными от нуля. Т. о., элемент сухого трения (рис. 1, е)моделирует предел текучести.
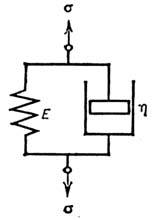
Рис. 2. Механическая модель Фойгта, состоящая из параллельно соединённых
пружины Е и поршня в цилиндре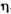
,
заполненном вязкой жидкостью.
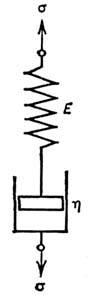
Рис. 3. Модель Максвелла с последовательным соединением пружины и поршня в цилиндре.
Приведённые элементарные модели обычно рассматриваются в Р. как составные части более сложных механич. моделей, отображающих реологич. поведение материала. Для того чтобы построить такие модели, эти элементы соединяют параллельно или последовательно. Так, двухэлементная модель Фойгта (рис. 2) качественно описывает явление упругого последействия, при к-ром деформация развивается с запаздыванием по отношению к приложенному напряжению. Модель Максвелла (рис. 3) удобна для качественного описания процессов релаксации напряжений. Обе эти модели линейны в том смысле, что для них удовлетворяется принцип суперпозиции, но они не обладают достаточной общностью, чтобы определить влияние предыстории состояния на поведение тела, т. е. не описывают явление памяти.
Для более точного описания наследств. свойств линейных материалов применяют
более сложные модели. Вязко-упругое тело - твёрдое тело, проявляющее запаздывающую
упругость, можно описывать моделью Кельвина (рис. 4); при деформировании
такого тела часть энергии необратимо рассеивается в виде теплоты. Вязкопластичное
тело, к-рое не деформируется при напряжениях, меньших нек-рого критич.
значения, а при больших - течёт как вязкая жидкость, описывается моделью
Б и н г а м а (рис. 5), представляющей собой параллельное соединение элементов
Ньютона и Сен-Венана.
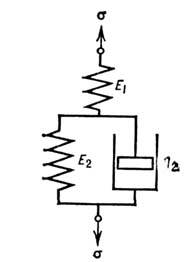
Рис. 4. Модель Кельвина: последовательное соединение элементов Гука
и Фойгта.
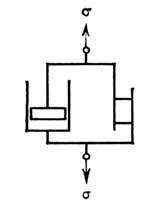
Рис. 5. Модель Бингама: параллельное соединение жидкостного элемента (поршень в цилиндре) и тела Сен-Венана.
Течение вязкопластич. тела описывается ур-ниями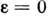
,
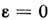, есл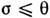и
,
и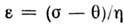
, если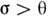
С проблемами Р. приходится встречаться при разработке технологии разнообразных производств. процессов, при проектных работах и конструкторских расчётах, относящихся к разл. материалам (особенно при высоких темп-pax): полимерам, композиционным материалам, бетонам, силикатам, пищевым продуктам и др. Методы Р. стали применяться для целей оперативного управления технологич. процессами. При этом осуществляется непрерывное или периодич. измерение одного пли неск. реологич. свойств сырья и (или) продукта по заданной программе, иногда с применением ЭВМ; с использованием обратной связи проводится корректирование в заданных пределах параметров сырья, процесса или дозирование поступающих ингредиентов.
Определяющие соотношения гидродинамики имеют ограниченное применение
в Р., поскольку реальные среды обладают аномалией вязкости (напр., вязкость
зависит от давления и температуры среды, скорости её течения). Проявляется
также зависимость напряжённо-деформированного состояния среды в данный
момент времени от всей предыстории напряжений (или деформаций). Предметом
изучения Р. выступают такие явления, приводящие к аномалии вязкости, как
т и к с о т р о п и я - способность нек-рых дисперсных систем (напр., коагуляц.
структур) обратимо разжижаться при достаточно интенсивных механич. воздействиях
(перемешивании, встряхивании) и отвердевать (терять текучесть) при пребывании
в покое; реопексия - ускорение нарастания прочности и структурирования
дисперсных систем при приложении небольших напряжений и деформировании
с небольшой скоростью; дилатансия (у концентрированных дисперсных систем
типа паст) - возрастание эффективного коэф. вязкости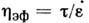
(где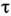
-
касат. напряжение,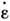
- скорость деформации сдвига) с увеличением скорости деформирования, сопровождающееся
нек-рым увеличением объёма, занимаемого системой (твёрдые частицы при деформировании
образуют более рыхлый каркас, и имеющейся жидкой среды оказывается недостаточно,
для того чтобы обеспечить системе подвижность).
Экспериментальная Р. (реометрия) определяет разл. реологич. свойства веществ с помощью спец. приборов и испытат. машин. Микрореология исследует деформации и течение в микрообъёмах, напр. в объёмах, соизмеримых с размерами частиц дисперсной фазы в дисперсных системах или с размерами атомов и молекул. Биореология изучает течение разнообразных биол. жидкостей (напр., крови, синовиальной и плевральной жидкостей), деформации разл. тканей (мышц, костей, кровеносных сосудов) у человека и животных. Изучение взаимодействия реологич. течений с электрич. и магн. полями, к-рые могут воздействовать на потоки как активно, так и путём их влияния на реология, характеристики вещества, составляет предмет электрореологии и магнитореологии.
Н. И. Малинин
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|
 |
