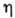 ,
обычно называемый вязкостью, определяется как коэф. пропорциональности между скоростью деформации
сдвига
,
обычно называемый вязкостью, определяется как коэф. пропорциональности между скоростью деформации
сдвига 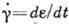 (
(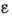 -
относит. деформация сдвига, t - время деформации) и возникающим при этом
касательном вязком напряжении
-
относит. деформация сдвига, t - время деформации) и возникающим при этом
касательном вязком напряжении 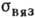 :
:Вязкость - переноса явления, определяющие диссипацию энергии при деформации среды. Вязкость при деформациях сдвига наз. сдвиговой вязкостью, при деформации всестороннего сжатия - объёмной вязкостью, при одноосном растяжении - продольной вязкостью. Рассеяние энергии при сдвиговой вязкости происходит вследствие переноса импульса, при объёмной - путём обмена энергией между степенями свободы при изменении объёма. В результате вязкости возникают напряжения, пропорциональные скоростям деформаций. Количественной характеристикой вязкости являются коэффициент вязкости.
Коэффициент сдвиговой вязкости 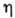 ,
обычно называемый вязкостью, определяется как коэф. пропорциональности между скоростью деформации
сдвига
,
обычно называемый вязкостью, определяется как коэф. пропорциональности между скоростью деформации
сдвига 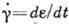 (
(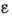 -
относит. деформация сдвига, t - время деформации) и возникающим при этом
касательном вязком напряжении
-
относит. деформация сдвига, t - время деформации) и возникающим при этом
касательном вязком напряжении 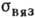 :
:
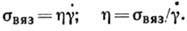
Это соотношение, установленное
И. Ньютоном (I. Newton), справедливо только в том случае, когда 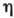 не зависит от скорости деформации. Среды, для к-рых выполняется это условие,
наз. ньютоновскими (см. Ньютоновская жидкость ).Коэф. сдвиговой
вязкости равен импульсу, переносимому в единицу времени через единицу площади при
не зависит от скорости деформации. Среды, для к-рых выполняется это условие,
наз. ньютоновскими (см. Ньютоновская жидкость ).Коэф. сдвиговой
вязкости равен импульсу, переносимому в единицу времени через единицу площади при 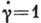 .
В системе СИ единица вязкости - паскаль-секунда [Па*с]. В гидродинамике часто пользуются понятием коэффициента
кинематической вязкости
.
В системе СИ единица вязкости - паскаль-секунда [Па*с]. В гидродинамике часто пользуются понятием коэффициента
кинематической вязкости 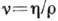 (
(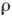 -плотность),
измеряемой в м2/с. Величину, обратную вязкости, иногда наз. текучестью.
-плотность),
измеряемой в м2/с. Величину, обратную вязкости, иногда наз. текучестью.
Если касательные напряжения,
возникающие в среде за счёт внеш. сил, поддерживаются равными вязким напряжениям,
то в среде установится постоянный во времени градиент скорости - возникает ламинарное
течение (рис. 1). Работа внеш. сил, уравновешивающих вязкие напряжения и поддерживающих
стационарный поток, полностью переходит в тепло. Коэф. сдвиговой вязкости 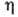 и мощность W, рассеиваемая в единице объёма за счёт вязкости, связаны соотношением
и мощность W, рассеиваемая в единице объёма за счёт вязкости, связаны соотношением
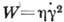 .
.
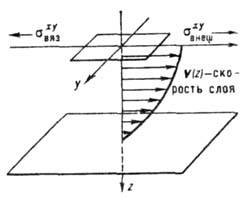
Рис. 1. Схема ламинарного течения вязкой жидкости.
Коэф. объёмной вязкости 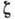 определяется как коэф. пропорциональности между скоростью объёмной деформации
и дополнит. давлением, возникающим в среде в результате нарушения термодинамич.
равновесия (см. Сжимаемость).
определяется как коэф. пропорциональности между скоростью объёмной деформации
и дополнит. давлением, возникающим в среде в результате нарушения термодинамич.
равновесия (см. Сжимаемость).
Коэф. продольной вязкости 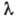 определяет поглощение продольных звуковых волн и является комбинацией
определяет поглощение продольных звуковых волн и является комбинацией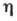
и 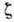 :
: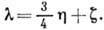
Статистич. теория необратимых
процессов позволяет получить 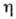 (а также
(а также 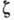 и
и 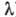 )
интегрированием по времени t автокорреляц. функций соответствующих потоков
или напряжений; для
)
интегрированием по времени t автокорреляц. функций соответствующих потоков
или напряжений; для 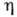 имеем:
имеем:
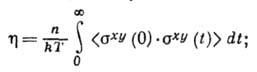
п - число частиц
в единице объёма. Автокоррелятор 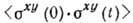 имеет простой физ. смысл: если в момент времени 0 в системе создаётся напряжение
имеет простой физ. смысл: если в момент времени 0 в системе создаётся напряжение
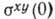 и затем она предоставляется
самой себе, то за счёт потока импульса через плоскость ху напряжение
будет меняться и к моменту времени t станет равным
и затем она предоставляется
самой себе, то за счёт потока импульса через плоскость ху напряжение
будет меняться и к моменту времени t станет равным 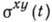 ; произведение этих двух значений напряжения, усреднённое по равновесному ансамблю
всех возможных конфигураций системы, и есть автокоррелятор напряжения. Поскольку
в каждый данный момент
; произведение этих двух значений напряжения, усреднённое по равновесному ансамблю
всех возможных конфигураций системы, и есть автокоррелятор напряжения. Поскольку
в каждый данный момент 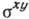 как раз равно потоку импульса через плоскость ху, то автокоррелятор потоков
импульса
как раз равно потоку импульса через плоскость ху, то автокоррелятор потоков
импульса 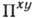 равен
автокоррелятору напряжения
равен
автокоррелятору напряжения
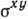 . Автокоррелятор
потоков импульса может быть вычислен с помощью кинетич. ур-ний. Для изотропной
молекулярной системы
. Автокоррелятор
потоков импульса может быть вычислен с помощью кинетич. ур-ний. Для изотропной
молекулярной системы
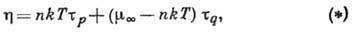
где 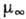 -т.
н. мгновенный модуль сдвига, определяющий мгновенную упругую реакцию среды;
-т.
н. мгновенный модуль сдвига, определяющий мгновенную упругую реакцию среды;
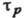 -время релаксации
по импульсам;
-время релаксации
по импульсам; 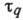 -время
релаксации по координатам.
-время
релаксации по координатам.
Для газов, как было показано
ещё Дж. Максвеллом (J. Maxwell), 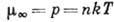 , где р - давление, и
, где р - давление, и 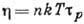 . Скорость релаксации по импульсам в этом случае определяется частотой молекулярных
соударений, и для идеального газа получим:
. Скорость релаксации по импульсам в этом случае определяется частотой молекулярных
соударений, и для идеального газа получим:
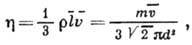
где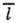 -
ср. длина свободного пробега,
-
ср. длина свободного пробега,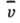 -
ср. скорость теплового движения молекул, т - масса, d -
диаметр молекулы. Вязкость такого газа не зависит от плотности или давления и растёт с температурой
пропорц.
-
ср. скорость теплового движения молекул, т - масса, d -
диаметр молекулы. Вязкость такого газа не зависит от плотности или давления и растёт с температурой
пропорц.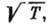 поскольку
поскольку
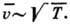 Зависимость вязкости
реальных газов от температуры и давления определяется отклонениями от идеального
состояния. Имеется
ряд эмпирич. и полуэмпирич. ф-л, описывающих зависимость вязкости реальных газов от
температуры и давления.
Зависимость вязкости
реальных газов от температуры и давления определяется отклонениями от идеального
состояния. Имеется
ряд эмпирич. и полуэмпирич. ф-л, описывающих зависимость вязкости реальных газов от
температуры и давления.
Вязкость низкомолекулярных жидкостей сильно зависит от температуры, падая с её
ростом. При не слишком высоких темп-pax
(близких к температуре плавления) кинетич. членами в ур-нии (*) можно пренебречь
и для сдвиговой вязкости жидкости принять: 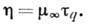
Сильная зависимость вязкости жидкости от температуры объясняется прежде всего температурной зависимостью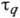 .
.
Для большинства жидкостей
зависимость вязкости от температуры при пост. давлении в узком интервале температур можно
описать ф-лой Андраде:
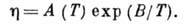
A (T)по сравнению
с 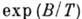 - слабая функция
от T. В нулевом приближении величину В связывают с энергией активации
молекулярного скачка
- слабая функция
от T. В нулевом приближении величину В связывают с энергией активации
молекулярного скачка 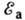 (см. Жидкость):
(см. Жидкость): 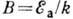 ,
а время релаксации по координатам считают равным ср. времени жизни частицы в
данном окружении (времени оседлости). Совр. исследования показали внутр. противоречивость
этой модели, и ф-лу Андраде и её разл. обобщения следует рассматривать как эмпирические.
,
а время релаксации по координатам считают равным ср. времени жизни частицы в
данном окружении (времени оседлости). Совр. исследования показали внутр. противоречивость
этой модели, и ф-лу Андраде и её разл. обобщения следует рассматривать как эмпирические.
Вязкость жидкостей при постоянной температуре обычно увеличивается с ростом давления. Исключение составляет вода,
у которой при температурах ниже 250C вязкость с ростом давления сначала
падает и проходит через минимум. Простые жидкости достаточно хорошо описываются
формулой Бачинского: 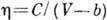 , где V - молярный объём, b - несжимаемый объём 1 моля, С - постоянная.
, где V - молярный объём, b - несжимаемый объём 1 моля, С - постоянная.
При пост. объёме вязкость зависит
от температуры гораздо слабее, чем при пост. давлении, и ф-ла Андраде неприменима.
При высоких температурах или при высоких давлениях кинетич.
членами в ур-нии (*) пренебрегать нельзя, и зависимость от температуры оказывается
достаточно сложной (рис. 2). Тот факт, что вязкость непосредственно определяется временем
релаксации по координатам 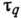 ,
объясняет корреляции в зависимостях вязкости и других физико-кинетических характеристик
жидкости, зависящих от
,
объясняет корреляции в зависимостях вязкости и других физико-кинетических характеристик
жидкости, зависящих от 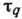 , например скоростей релаксации в ядерном магнитном резонансе.
, например скоростей релаксации в ядерном магнитном резонансе.
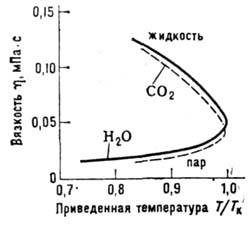
Рис. 2. Характер температурной
зависимости вязкости вещества в жидком и газообразном состояниях.
Вязкость воды при 20 0C
составляет 1,002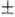 0,001
мПа*с, и это значение принимается как эталонное. Вязкость низкомолекулярных жидкостей,
расплавленных металлов и солей обычно не превышает неск. десятков Па*с. При
более высоких вязкостях жидкости перестают вести себя как ньютоновские и их
поведение следует рассматривать с общих позиций реологии и вязкоупругости.
0,001
мПа*с, и это значение принимается как эталонное. Вязкость низкомолекулярных жидкостей,
расплавленных металлов и солей обычно не превышает неск. десятков Па*с. При
более высоких вязкостях жидкости перестают вести себя как ньютоновские и их
поведение следует рассматривать с общих позиций реологии и вязкоупругости.
Вязкость растворов зависит от
концентрации растворённого вещества, прячем эта зависимость может быть достаточно
сложной, а вязкость раствора может быть и больше, и меньше вязкости чистого растворителя.
Вязкость предельно разбавленных суспензий линейно зависит от объёмной доли 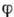 взвешенных частиц:
взвешенных частиц: 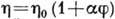 (ф-ла Эйнштейна);
(ф-ла Эйнштейна); 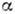 =
2,5 для частиц сферической формы,
=
2,5 для частиц сферической формы, 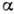 >2,5
для частиц вытянутой формы,
>2,5
для частиц вытянутой формы, 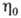 - вязкость дисперсионной среды.
- вязкость дисперсионной среды.
В расплавах и растворах
полимеров, а также в многокомпонентных системах наблюдаются сложные явления,
связанные с разрушением надмолекулярных структур при деформациях сдвига (см.,
напр., тиксотропия), и
поведение таких сред оказывается ньютоновым при малых касат. напряжениях и неньютоновым
при больших.
Сдвиговая и объёмная вязкость являются важнейшими техн. характеристиками веществ. Эксперим. методы определения
сдвиговой вязкости см. в ст. Вискозиметрия; объёмная вязкость определяется из измерения
поглощения звуковых и ультразвуковых волн.

Ю.П. Сырников
|
|