Индуктивное сопротивление в аэродинамике - часть аэродинамического сопротивления крыла, обусловленная вихрями, оси к-рых берут своё начало на крыле и направлены вниз по потоку.
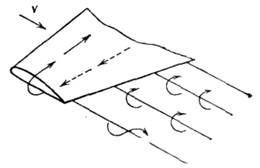
Рис. 1. Схема возникновения торцевого вихря в результате перетекания воздуха из области под крылом в область над крылом.
Эти т. н. свободные вихри происходят от перетекания воздуха у торцов
(рис. 1) из области под крылом в область над крылом. Течение воздуха у
торцов вызывает поток, направленный над крылом от торцов к плоскости симметрии,
а под крылом - от плоскости симметрии к торцам; в результате в спутной
струе, или следе, за крылом происходит вращение каждой частицы вокруг
оси, проходящей через неё и параллельной местному вектору скорости v
потока; направление вращения при этом противоположно для левого н
правого полукрыла (рис. 2). Т. о., возникает непрерывная система вихрей,
отходящих от каждой точки поверхности крыла. В случае крыла большого
удлинения можно считать, что свободные вихри образуют плоскую вихревую
пелену; для крыла малого удлинения вихревая система является
пространственной.
Свободные вихри вызывают (индуцируют) в области между торцами крыла
потоки, направленные вниз, к-рые, налагаясь на набегающий поток,
отклоняют последний вниз на угол Да (угол скоса потока). В результате
подъёмная сила элемента крыла, к-рая по
теореме Жуковского о подъёмной силе должна быть перпендикулярна
набегающему потоку, отклоняется назад на тот же угол (рис. 3). Разлагая
эту силу на компоненты вдоль v и перпендикулярно v, получаем индуктивное лобовое сопротивление и подъёмную силу.
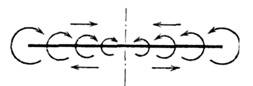
Рис. 2. Разрез потока за крылом плоскостью, перпендикулярной v.
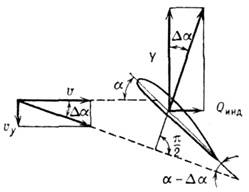
Рис. 3. Образование индуктивного сопротивления в результате скоса потока свободными вихрями крыла; vy - скорость, индуцированная свободными вихрями; Da - угол скоса.
И. с. и угол скоса потока могут быть вычислены, если в каждом сечении крыла известно распределение циркуляции скорости
по контуру, охватывающему профиль. В случае крыла большого удлинения в
потоке несжимаемой среды угол скоса и И. с. определяются ф-лами:
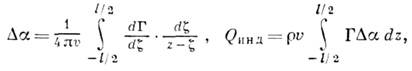
где l - размах крыла, r - плотность
среды, Г - циркуляция скорости по контуру, охватывающему данное сечение
крыла, z - расстояние сечения от ср. плоскости крыла, z - расстояние
оси свободного вихря от этой плоскости. Распределение циркуляции по
размаху должно удовлетворять интегродифференциальному ур-нию:
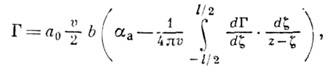
где а0 - производная от коэф. подъёмной силы по углу атаки для данного сечения крыла, b - хорда данного сечения, aа
- аэродинамнч. угол атаки (т. е. угол атаки, отсчитываемый от
направления, при к-ром подъёмная сила равна нулю). Ур-ние для Г(z)
обычно решается с помощью тригонометрич. рядов.
Безразмерный коэф. И. с. Сх инд связан с коэф. подъёмной силы Сy плоского крыла соотношением
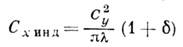
(l=l2/S - удлинение крыла, S
- площадь крыла в плане, d - величина, зависящая от распределения
циркуляции по размаху крыла). Если крыло имеет бесконечно большой размах
(l=:), И. с. отсутствует. Если циркуляция распределена вдоль размаха
крыла по эллиптич. законy, то d=0 и И. с. минимально.
И. Я. Фабрикант
Понятие же "физического вакуума" в релятивистской квантовой теории поля подразумевает, что во-первых, он не имеет физической природы, в нем лишь виртуальные частицы у которых нет физической системы отсчета, это "фантомы", во-вторых, "физический вакуум" - это наинизшее состояние поля, "нуль-точка", что противоречит реальным фактам, так как, на самом деле, вся энергия материи содержится в эфире и нет иной энергии и иного носителя полей и вещества кроме самого эфира.
В отличие от лукавого понятия "физический вакуум", как бы совместимого с релятивизмом, понятие "эфир" подразумевает наличие базового уровня всей физической материи, имеющего как собственную систему отсчета (обнаруживаемую экспериментально, например, через фоновое космичекое излучение, - тепловое излучение самого эфира), так и являющимся носителем 100% энергии вселенной, а не "нуль-точкой" или "остаточными", "нулевыми колебаниями пространства". Подробнее читайте в FAQ по эфирной физике.
|
|
 |
