 ].
].Молекула (от новолат. molecula, уменьшит. от лат. moles - масса) - наименьшая устойчивая частица вещества, обладающая
его осн. химическими и физическими свойствами. Состоит из атомных ядер и электронов, связанных
между собой эл--магн. силами; можно также считать молекулу системой атомов, связанных
друг с другом разл. связями (см. Межатомное взаимодействие).
Представление о молекуле возникло в 18 в. и с развитием
в 19 в. кинетич. теории газов и становлением термодинамики получило широкое
распространение. Прямое экспериментальное подтверждение существования
молекул провёл Ж. Перрон (J. Perrin) при изучении броуновского движения (1906).
Молекулярные вещества в газовой и жидкой фазах
и в молекулярных кристаллах сохраняют индивидуальность.
В расплавах и ионных кристаллах молекулы, как правило, утрачивают индивидуальность,
т. к. каждый атом в них связан с большим числом окружающих его атомов.
Химическая формула молекулы - брутто формула - указывает все
входящие в неё атомы хим. символами элементов, а также число одинаковых атомов.
Порядок расположения атомов в молекуле и характер связи между ними отражает
структурная ф-ла молекулы.
Молекула образуется из атомов при их сближении, если
энергия связанного состояния меньше суммы энергий свободных атомов. Выделяемая
при образовании молекулы энергия может передаваться др. частицам (переходить в тепло)
или испускаться в виде кванта света (хемилю-минесцснция), Соответственно,
для отрыва от молекулы отд. атомов или атомных групп необходимо сообщить молекуле
определ. энергию (энергию диссоциации). Число атомов в молекуле составляет от двух
(H2, O2, HCl, СО) до сотен и тысяч (нек-рыe витамины,
гормоны, белки).
Энергия отдельных химических связей в молекуле составляет
неск. эВ. Связь между атомами в молекуле осуществляется электронами незамкнутых оболочек
(валентными электронами) так, чтобы система была электронейтральной, а электронная
оболочка - замкнутой. Атомы с замкнутыми в основном состоянии оболочками могут
образовывать хим. связи, если их перевести в возбуждённое состояние.
Образующиеся при этом молекулы (напр., He*2) являются
метастабильными и наз. эксимерными.
Молекулы с открытыми (незамкнутыми) электронными оболочками
(напр., ОН, CH2, NH2) наз. радикалами (свободными радикалами).
Молекулы и радикалы с нескомпенсированным электрич. зарядом, получающиеся при отрыве
или присоединении электронов к нейтральной молекуле.
(напр., H+2, H-2),
наз. молекулярными (радикальными) нонами. Радикалы и ионы образуются как промежуточные
продукты хим. реакций, при разл. воздействиях на молекулы и в обычных условиях неустойчивы,
но в изолиров. состоянии (напр., в космич. пространстве) могут существовать
долго.
Близкими к молекулам образованиями являются ван-дер-ваальсовские
комплексы (HCl.Ar), молекулярные ассоциаты, ионные кластеры, ван-дер-ваальсовы
молекулы и т. д., связанные между собой более слабыми, чем химические, связями
- водородными или ван-дер-ваальсовыми. Комплексы могут состоять из двух, трёх
и т. д. Молекулы [(H2O)2, (NaCl)4], их называют димерами,
три-мерами и т. д. Ионные кластеры образуются из иона H+3
и молекул H2 [напр., 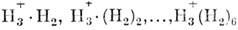 ].
].
Такие системы неустойчивы и распадаются под внеш.
воздействием.
В молекуле между валентными электронами в основном
состоянии преобладает обменное взаимодействие, к-рое выстраивает спины электронов
антипараллельно, поэтому осн. электронное состояние большинства молекул синглетное,
Молекула диамагнитна. Свободные радикалы обычно парамагнитны.
В зависимости от числа валентных
электронов, принимающих участие в хим. связи, последние наз. одинарными, двойными
и тройными. Напр., атомы С в молекуле этана C2H6 связаны одинарной
связью С - С, в молекуле этилена C2H4 - двойной связью C = C,
а в молекуле ацетилена C2H2 - тройной связью C=C. Одинарная
связь образуется двумя валентными электронами (s-электроны), двойная связь
- четырьмя электронами (p-электроны),
а тройная связь - шестью электронами (также p-электроны).
Электроны внутр. замкнутых оболочек атомов практически не участвуют в хим. связи.
Такая классификация хим. связей условна и не всегда приемлема. Она лучше всего
подходит для классификации связей в разветвлённых (насыщенных) углеводородах
и неприменима к циклич. углеводородам типа бензола (C6H6),
т. к. в этом случае шесть одинаковых связей между атомами С, наз. также сопряжёнными
связями, образуются за счёт 18 валентных электронов и рассмотренная классификация
привела бы к полуторным связям.
В нек-рых случаях хим. связи образуются нечётным
числом электронов. Так, в стабильном ионе H+2
связь образована одним электроном, в ионе
H+3, имеющем структуру
равностороннего треугольника, три связи H - H образованы всего двумя электронами
и т. д. Кроме того, не все электроны внеш. электронной оболочки атомов принимают
участие в хим. связи. Напр., в молекуле NH3 два из пяти внеш. электрона
атома N не принимают участия в образовании связей и наз. неподелённой парой
электронов. Бели при образовании связи между атомами А и Б электрон переносится
от А к Б (или обратно), то связь между A и Б наз. ионной (напр., NaCl), а если
валентные электроны распределены между А и Б равномерно, то связь А - Б наз.
ковалент-ной (напр., H - H, С - С). Обычно ковалентные связи прочнее ионных.
В сопряжённых системах типа бензола электроны, связывающие атомы С, равномерно
распределены по всему кольцу.
Форма молекулы определяется пространств. расположением
атомов в ней, к-рое в свою очередь определяется величинами длин связей и углов
между связями (валентных углов). Между кратностью и длиной связи существует
корреляция: связь между определ. атомами укорачивается с ростом её кратности.
Напр., типичные величины длин связей С - С,С = С и С = С соответственно
равны 1,50, 1,35 и 1,20 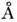 .
Длина связи зависит от её хим. окружения в молекуле. Напр., длина связи С - H в группе
- CH3 составляет ок. 1,10
.
Длина связи зависит от её хим. окружения в молекуле. Напр., длина связи С - H в группе
- CH3 составляет ок. 1,10 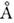 ,
а в группах =СН2 и =CH 1,08 и 1,05
,
а в группах =СН2 и =CH 1,08 и 1,05 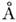 соответственно. Валентные углы между связями бывают самые разные, причём углы
между одними и теми же связями в различных молекулах могут быть различными, хотя определ.
характеристичность существует и для углов. Напр., угол между связями С-H в группе
-CH3, входящей в различные молекулы, часто близок к 109°. Если атом С образует
четыре связи, то углы между этими связями близки к тетраэдрич. углу (109°
30'). Для качеств. описания формы молекул, содержащих атом С, важное значение имеет
гибридизация атомных орбиталей С (см. Молекулярная орби-таль), т. е.
образование из пары орбиталей внешних s-электронов и пары орбиталей р-электронов
четырёх эквивалентных линейных комбинаций, наз. гибридными орбиталями.
соответственно. Валентные углы между связями бывают самые разные, причём углы
между одними и теми же связями в различных молекулах могут быть различными, хотя определ.
характеристичность существует и для углов. Напр., угол между связями С-H в группе
-CH3, входящей в различные молекулы, часто близок к 109°. Если атом С образует
четыре связи, то углы между этими связями близки к тетраэдрич. углу (109°
30'). Для качеств. описания формы молекул, содержащих атом С, важное значение имеет
гибридизация атомных орбиталей С (см. Молекулярная орби-таль), т. е.
образование из пары орбиталей внешних s-электронов и пары орбиталей р-электронов
четырёх эквивалентных линейных комбинаций, наз. гибридными орбиталями.
Нек-рые представления о форме и геометрич. симметрии
молекулы, состоящей из данного набора атомов, можно получить на основе симметрии молекулы
и концепции молекулярных орбиталей (МО). В зависимости от знака вклада, вносимого
электроном данной МО в полную энергию молекулы, МО наз. разрыхляющими или связывающими:
связывающие участвуют в образовании прочных хим. связей, а разрыхляющие - не
участвуют. Число связывающих и разрыхляющих МО зависит только от симметрии расположения
атомов в молекуле. Поэтому определение устойчивой формы молекулы сводится к нахождению такого
расположения атомов, к-рому соответствует наиб. число связывающих МО. Напр.,
в случае CH4 для тетраэдрич. расположения четырёх атомов H вокруг
С (симметрия Td)получается наиб. число связывающих МО - 8
(напр., для симметрии C3u
их 6). Разл. МО вносят разный вклад в энергию, и поэтому этот метод но всегда
применим, но в большинство случаев он правильно предсказывает геом. симметрию
молекулы (напр., он позволяет установить, что молекула H2O - нелинейная,
молекула CO2 - линейная), особенно геом. симметрию молекул в возбуждённых электронных состояниях.
Структурные параметры для осн. электронного состояния мн. молекул определены методами
газовой электронографии, микроволновой спектроскопии
и др. спектральными методами.
В зависимости от изотопич. состава атомов молекула имеет изотопич. модификации. Напр., CH3D, CH2D2,
CHD3, CD4 являются изотопич. модификациями метана (CH4).
Структурные параметры изотопич. модификаций очень близки к структурным параметрам
основной молекулы, а малые отличия (~ 0,01 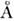 в длинах связей и ~1° в валентных углах) обычно обусловлены различием колебат.
поправок к структурным параметрам. Кроме того, низкосимметричные изотопич. модификации
неполярных молекул могут быть слабо полярными с дипольным моментом ок. 0,01 дебая.
в длинах связей и ~1° в валентных углах) обычно обусловлены различием колебат.
поправок к структурным параметрам. Кроме того, низкосимметричные изотопич. модификации
неполярных молекул могут быть слабо полярными с дипольным моментом ок. 0,01 дебая.
В соответствии с симметрией равновесной конфигурации молекул, можно разделить на три класса: 1) Молекулы, не имеющие осей симметрии 3-го пли более высокого порядка; 2) Молекулы, имеющие одну ось симметрии 3-го или более высокого порядка; 3) Молекулы, имеющие неск. осей симметрии 3-го или более высокого порядка (см. Симметрия молекул). Молекулы этих классов наз. асимметричными, симметричными и сферич. волчками соответственно. Линейная молекула является частным случаем симметричного волчка.
Уровни энергии молекул определяются из решения полного Шрёдингера уравнения методами
квантовой химии. Численные решения ур-ния Шрёдингера выполнены только
для очень простых молекул (H+2
H2), для остальных молекул проводится приближённое разделение ур-ния Шрёдингера
на отдельные yp-ния для электронной и ядерной подсистем. Такое разделение проводят
на основании Борна - Оппенгеймера теоремы. Решение ур-ния Шрёдингера
для электронов даёт электронные уровни энергии молекулы в зависимости от координат
ядер как от параметров (см. Потенциальная поверхность ),а ур-ниe Шрёдингера
для ядер - колебательно-вращательные уровни энергии в разл. электронных состояниях.
Ур-ние Шрёдингера для ядер также разделяют на колебательное и вращательное.
Электронная энергия молекулы в 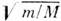 (т - масса электрона, M - масса ядра) раз больше колебательной,
к-рая в
(т - масса электрона, M - масса ядра) раз больше колебательной,
к-рая в 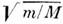 раз больше
вращательной, что и позволяет произвести такое разделение. Взаимодействия между
разл. видами движений (электронными, колебательными, вращательными) очень важны
и составляют осн. предмет исследований в совр. молекулярной спектроскопии.
раз больше
вращательной, что и позволяет произвести такое разделение. Взаимодействия между
разл. видами движений (электронными, колебательными, вращательными) очень важны
и составляют осн. предмет исследований в совр. молекулярной спектроскопии.
Полные электронно-колебательно-вращательныо (рови-бронные)
уровни энергии молекулы классифицируют по неприводимым представлениям (типам симметрии)
группы симметрии молекулы. Разделение полного движения на отд. виды дает возможность
ввести приближённые квантовые числа для классификации уровней молекулы.
В большинстве случаев эти числа связаны с собств. значениями квадратов и z-проекций
соответствующих угл. моментов. В спектроскопии двухатомных молекул используются угл.
моменты и их квантовые числа, приведённые в табл.

Для линейных многоатомных молекул, симметричных и
сферич. волчков кроме упомянутых угл. моментов используются также колебат. угл.
моменты lt для каждого вырожденного колебания и полный колебат.
угл. момент 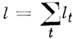 .
Для симметричных волчков важное значение имеет квантовое число К проекции
вращат. угл. момента на выделенную ось симметрии молекул; К = 0 в невырожденных
колебат. состояниях и К = l в вырожденных колебат. состояниях
линейных молекул. Для асимметричных волчков К теряет смысл, а для обозначения
вращат. уровней используют символ JKаКc , где Ка и Кс являются проекц. квантовыми числами для предельных
случаев вытянутого (a) и сплюснутого (с)симметричного волчка.
Для сферич. волчков К также но имеет смысла, и вместо него используют
типы симметрии уровней с данными J и их кратность.
.
Для симметричных волчков важное значение имеет квантовое число К проекции
вращат. угл. момента на выделенную ось симметрии молекул; К = 0 в невырожденных
колебат. состояниях и К = l в вырожденных колебат. состояниях
линейных молекул. Для асимметричных волчков К теряет смысл, а для обозначения
вращат. уровней используют символ JKаКc , где Ка и Кс являются проекц. квантовыми числами для предельных
случаев вытянутого (a) и сплюснутого (с)симметричного волчка.
Для сферич. волчков К также но имеет смысла, и вместо него используют
типы симметрии уровней с данными J и их кратность.
Разл. электронные уровни с заданным L линейной молекулы обозначают S, П, D, F, ... в соответствии со значениями
L = 0,1,2,3,... Между типами симметрии и значениями L имеется взаимно
однозначное соответствие, поэтому неприводимые представления точечных групп
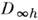 и
и 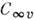 также
обозначаются S , П, D, F. Мультиплет-ность уровня, определяемая
значениями 2S + 1, записывается слева сверху L. Напр., 3S
обозначает уровень с L
= 0 и S = 1, а 2П обозначает уровень с L
= 1 и S = 1/2. К этому символу добавляется
значение J, N или F для каждого вращат. подуровня, а если необходимо,
то ещё и номер колебат. уровня u. Для нелинейных молекул L
не имеет смысла, вместо L
используется тип симметрии, а остальные обозначения сохраняются.
также
обозначаются S , П, D, F. Мультиплет-ность уровня, определяемая
значениями 2S + 1, записывается слева сверху L. Напр., 3S
обозначает уровень с L
= 0 и S = 1, а 2П обозначает уровень с L
= 1 и S = 1/2. К этому символу добавляется
значение J, N или F для каждого вращат. подуровня, а если необходимо,
то ещё и номер колебат. уровня u. Для нелинейных молекул L
не имеет смысла, вместо L
используется тип симметрии, а остальные обозначения сохраняются.
В простейшем приближении каждому нормальному
колебанию молекул vk сопоставляется гармонический осциллятор
с энергией

где wk
- волновое число, uk
- колебат. квантовое число. Состояние молекулы, в к-ром возбуждено неск. колебаний,
обозначают набором чисел uk.
Напр., состояние (1, 2, 1) молекула H2O характеризуется числами u1
= 1, u2
= 2 и u3 = 1 (иногда такое состояние обозначают v1 + 2v2
+ v3). Если возбуждены вырожденные колебания, то квантовые
числа ut снабжаются также верхним индексом ls, указывающим квантовое
число колебат. углового момента, равное but,
b(ut - 2), ...: напр., состоянию (2,3b1,
1) отвечают квантовые числа u1 = 2, u2
= 3, l2 = b1, u3
= 1.
Вращат. уровни молекулы качественно описываются в рамках модели жёсткого волчка.
Вращат. энергия жёсткой (т. е. колебания её атомных ядер незначительны)
двухатомной молекулы в 1S-состоянии
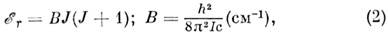
где В - вращат. постоянная, I -
момент инерции. Ф-ла (2) справедлива также для жёсткой линейной молекулы и для жёсткого
сферич. волчка в 1S-состоянии,
причём каждый J - уровень сферич. волчка (2J+1) - кратно
вырожден по проекции J на одну из осей молекулы (для линейной молекулы эта
проекция равна нулю). Для жёсткого симметричного волчка два из трёх гл. моментов
инерции равны между собой и энергия
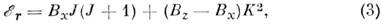
где z - выделенная ось симметрии волчка,
а ось x перпендикулярна z. Оси инерции молекулы принято обозначать также буквами
а, b, с, причём Ia <= Ib
<= Iс, a вращат. постоянные буквами A >= В >=
С. В зависимости от соответствия между осями х, у, z и а, b,
с симметричные волчки разделяются на два класса - вытянутые, для к-рых энергия
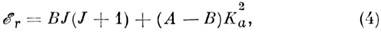
и сплюснутые, для к-рых
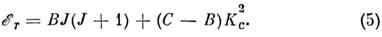
В качестве оси квантования вращат. угл. момента
в (4) выбрана ось a (Ib= Iс), а в
(5) - ось с (Ia = Ib).
При промежуточных значениях В уровни с
разд. значениями пары чисел Ка, Кс при заданном
J не пересекаются, поэтому символ JKaKc является однозначной
характеристикой вращат. уровней асимметричного волчка, когда Iа 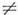 Ib
Ib 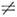 Ic. Числа J, Ка и Кс тесно связаны
с числом и ориентацией узлов волновой функции асимметричного волчка. Энергия увеличивается
с ростом Ка и уменьшается с ростом Kc, т.
е. энергия растёт в соответствии с последовательностью квантовых чисел:
Ic. Числа J, Ка и Кс тесно связаны
с числом и ориентацией узлов волновой функции асимметричного волчка. Энергия увеличивается
с ростом Ка и уменьшается с ростом Kc, т.
е. энергия растёт в соответствии с последовательностью квантовых чисел:
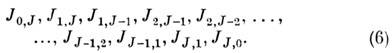
Сумма Ка + Кс равна J (при чётном J)или J + 1 (при нечётном J).
Асимметрия волчка характеризуется параметром:
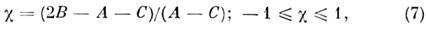
к-рый равен -1 для вытянутого и +1 для сплюснутого
симметричных волчков. Поэтому вместо JKaKc пишут также JK-1K+1. Энергия асимметричного волчка определяется только численно как собств. значения
матрицы энергии, записанной в базисе волновых функций симметричного волчка. Отличные
от нуля элементы этой матрицы равны:
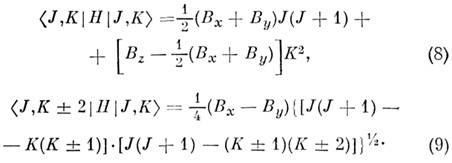
Вырождение уровней по знаку Ка и Кс, присущее симметричному волчку, для асимметричного
волчка снимается недиагональными элементами в (9). Получающееся при этом расщепление
наз. K-удвоением: величина K-удвоения максимальна при К = 1
и падает с ростом К.
Модель жёсткого волчка является грубым приближением
к реальной молекулы. Реально молекула при вращении искажается, и такое центробежное искажение
даёт существенный вклад в её энергию. В случае двухатомной молекулы основная (квартичная)
центробежная поправка к (3) равна

где DJ = 4В3/w2,
и если В = 1 см-1 и w = 1000 см-1, то DJ
= 4·10-6 см-1 = 120 кГц, поправка к энергии при J
= 10 равна 1,2 ГГц. Для сферич. волчка (напр., молекула CH4) квартичиая
центробежная поправка состоит из двух частей:
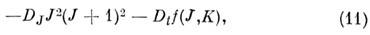
из к-рых первая - изотропная и не зависит от
проекции J, а вторая - анизотропная и расщепляет уровень с заданным J
на подуровни разл. типов симметрии. Напр., для CH4 Dt = 132 кГц и уровень с J= 2 расщепляется на компоненты с интервалом
между ними 60 Dt . функция f(J, К)определяется
численно. Она ~J4, и расщепление быстро растёт с ростом J:
при заданном J её мин. значение равно -4J2(J
+ 1)2, а макс. значение равно +8J2(J + 1)2.
Для симметричных волчков центробежная поправка
также состоит из двух частой, из к-рых первая
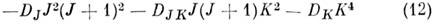
сдвигает уровни, а вторая, зависящая от симметрии
молекулы, может приводить к снятию вырождения уровней по знаку К. Для асимметричных
волчков центробежная поправка к энергии определяется только численно. Константы
квартичного центробежного искажения зависят от квадратичных членов разложения
потенциальной поверхности и используются для определения гармонич. силовых
постоянных молекулы. Обычно из вращат. спектров молекул определяются также константы центробежных поправок
более высокого порядка (секстичные, октичные и др.), к-рые содержат информацию
о константах энгармонизма молекул.
В гармоническом приближении энергия колебат. уровней молекулы определяется суммой выражений типа (1)
по всем нормальным колебаниям, к-рые возбуждены в данном состоянии:
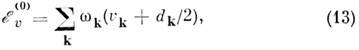
где dk - степень вырождения
k-го колебания. Для молекул типа асимметричного волчка все гармонич.
колебат. состояния невырождсны и энгармонизм только сдвигает их, как правило,
вниз. Кубич. и квартичные члены разложения потенц. поверхности во втором приближении
теории возмущении дают след. вклад в энергию:
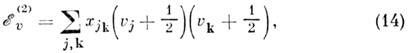
где xjk. - постоянные ангармоничности, к-рые составляют обычно 1 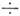 10 см-1, но для лёгких атомов возрастают до 100 см-1.
В гармонич. приближении (13) энергия колебат. уровней не зависит от колебат.
угловых моментов lt. Поэтому состояния молекул типа симметричного
и сферич. волчков, в к-рых возбуждены вырожденные колебания, могут быть вырожденными.
Это вырождение частично снимается энгармонизмом, и получающееся расщепление
называется ангармонич. расщеплением. Для молекул такого типа энергия колебат. уровней
рассчитывается по более общей, чем (14), ф-ле:
10 см-1, но для лёгких атомов возрастают до 100 см-1.
В гармонич. приближении (13) энергия колебат. уровней не зависит от колебат.
угловых моментов lt. Поэтому состояния молекул типа симметричного
и сферич. волчков, в к-рых возбуждены вырожденные колебания, могут быть вырожденными.
Это вырождение частично снимается энгармонизмом, и получающееся расщепление
называется ангармонич. расщеплением. Для молекул такого типа энергия колебат. уровней
рассчитывается по более общей, чем (14), ф-ле:
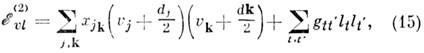
в к-рой ангармонич. расщепление уровней представлено
вторым членом. Напр., в молекулах с симметрией C3u
(напр., NH3) уровень с ut= 2, lt = 0, b2 (все остальные uk
= 0) расщепляется на подуровни с lt =0 и lt=b2
с интервалом между ними 4gtt', а уровень с ut
= 1, lt = b1 и ut'
=1, lt' = b1 расщепляется на подуровни
с lt + lt' = 0 и lt =
b2 с интервалом между ними 2gtt'. Ангармонич. расщепления
вырожденных колебат. уровней молекул типа симметричного и сферич. волчков (BF3,
SF6 и т. д.) играют важную роль в многофотонном поглощении ИК-излучения.
Ф-лы (14) и (15) справедливы при отсутствии т.
н. ангармонич. резонансов. Если осн. гармонич. частота wk
равна или близка к составной гармонич. частоте wi + wj
и коэф. ангармоничности Kijk 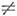 0, то ангар-монизм приводит к сильному перемешиванию состояний и аномальному
сдвигу уровней, наз. случайными ангармонич. резонансами (или резонансами Ферми).
Впервые такой эффект наблюдэлся в спектре комбинац. рассеяния света молекулами CO3
и был интерпретирован Э. Ферми (E. Fermi) в 1931: сильное перемешивание состояний
с u1 = 1 и u2l2
=20 приводит к появлению в спектре комбинац.
рассеяния двух полос v1 и 2v2 вблизи 1200
см-1 с близкой интенсивностью (в отсутствие резонанса полоса 2v2
должна была быть намного слабее).
0, то ангар-монизм приводит к сильному перемешиванию состояний и аномальному
сдвигу уровней, наз. случайными ангармонич. резонансами (или резонансами Ферми).
Впервые такой эффект наблюдэлся в спектре комбинац. рассеяния света молекулами CO3
и был интерпретирован Э. Ферми (E. Fermi) в 1931: сильное перемешивание состояний
с u1 = 1 и u2l2
=20 приводит к появлению в спектре комбинац.
рассеяния двух полос v1 и 2v2 вблизи 1200
см-1 с близкой интенсивностью (в отсутствие резонанса полоса 2v2
должна была быть намного слабее).
Ангармонич. резонансы наблюдаются и при wi
b wj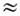 wk
b wl,
wi
wk
b wl,
wi 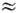 wj b
wk
b wl
и т. д., если отличны от нуля соответствующие
коэффициенты ангармоничности. Ангармонические резонансы могут иметь место только
между колебат. уровнями одинакового типа симметрии.
wj b
wk
b wl
и т. д., если отличны от нуля соответствующие
коэффициенты ангармоничности. Ангармонические резонансы могут иметь место только
между колебат. уровнями одинакового типа симметрии.
Вращат. уровни возбуждённых невырожденных колебат. состояний
отличаются от вращат. уровней осн. состояния только тем, что величины вращат.
и центробежных постоянных немного (на 0,1 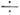 1%)
отличаются от их величин для осн. состояния, хотя при наличии случайных резонансов
вращат. структура возбуждённого состояния может быть сильно деформированной.
Качеств. отличие вращат. структуры вырожденных колебат. состояний от вращат.
структуры невырожденных состояний определяется прежде всего наличием в вырожденных
состояниях колебат. угловых моментов lt. Для симметричного
волчка взаимодействие lt с вращат. угловым моментом J
(наз. также ко-риолисовым взаимодействием) вносит вклад в энергию, к-рый в первом
приближении равен:
1%)
отличаются от их величин для осн. состояния, хотя при наличии случайных резонансов
вращат. структура возбуждённого состояния может быть сильно деформированной.
Качеств. отличие вращат. структуры вырожденных колебат. состояний от вращат.
структуры невырожденных состояний определяется прежде всего наличием в вырожденных
состояниях колебат. угловых моментов lt. Для симметричного
волчка взаимодействие lt с вращат. угловым моментом J
(наз. также ко-риолисовым взаимодействием) вносит вклад в энергию, к-рый в первом
приближении равен:
 где Szt - постоянные кориолисова взаимодействия,
зависящие от формы нормальных колебаний и структурных
парэметров молекулы. Кориолисово взаимодействие даёт вклад в ангармонич. расщепление
уровней с различными |lt|. Кроме того, оно расщепляет уровень
с bК, b l от уровня с bК, bl, но
уровни с +К, +l и -К, -l, а также уровни с +К, -l и
-К, +l остаются вырожденными: это вырождение снимается эффектами
колеба-тельно-вращат. взаимодействия более высокого порядка.
В частном случае молекул симметрии C3u
при К = lt = b1 (или Klt =
+1) происходит расщепление на подуровни величиной qtJ(J + 1),
получившей назв. l-удвоения; константа l-удвоения qt зависит от кубич. коэф. ангармоничности. Такое удвоение имеет место и для
линейных молекул, для к-рых, однако, qt зависит только от
гармонич. части потенц. поверхности.
где Szt - постоянные кориолисова взаимодействия,
зависящие от формы нормальных колебаний и структурных
парэметров молекулы. Кориолисово взаимодействие даёт вклад в ангармонич. расщепление
уровней с различными |lt|. Кроме того, оно расщепляет уровень
с bК, b l от уровня с bК, bl, но
уровни с +К, +l и -К, -l, а также уровни с +К, -l и
-К, +l остаются вырожденными: это вырождение снимается эффектами
колеба-тельно-вращат. взаимодействия более высокого порядка.
В частном случае молекул симметрии C3u
при К = lt = b1 (или Klt =
+1) происходит расщепление на подуровни величиной qtJ(J + 1),
получившей назв. l-удвоения; константа l-удвоения qt зависит от кубич. коэф. ангармоничности. Такое удвоение имеет место и для
линейных молекул, для к-рых, однако, qt зависит только от
гармонич. части потенц. поверхности.
Численные значения энергий электронных уровней молекулы определяются методами квантовой химии,
число же уровней разл. типов симметрии и их относит. расположение могут быть
найдены на основе модельных представлений и соображе-ний симметрии.
Если рассматривать молекулу как объединённый атом (о. а.) или более простую объединённую молекулу (о. м.) с
тем же числом электронов, то возможные электронные уровни рэзл. типов симметрии
точечной группы молекул можно определить, рассматривая расщепление электронных уровней
о. а. или о. м. в электрич. поле искомой M. или просто корреляцию между уровнями
о. а. и M. или же о. м. и M., к-рая легко определяется из характеров точечных
групп. Напр., о. а. для CH4 является этом Ne, а первые три уровня
1Sg, 3Pu, 1Pu
коррелируют с уровнями типa 1A1, 3F2,
1F2 M. CH4 соответственно, т.
е. основным уровнем CH4 является уровень 1A1, первое возбуждённое состояние 3Pu этома Ne
приводит к 3F2-состоянию CH4 и т.д.
Ясно, что коррелируют уровни о. а. и M. с одинаковой мультиплет-ностью. Это
справедливо, пока спин-орбитальное расщепление мало, а если же оно велико, то
необходимо проводить корреляцию между полными волновыми функциями, учитыва-ющими
спин.
Электронные уровни M. можно получить также из
уровней разъединённых атомов (р. а.) или групп зто-мов по векторной модели.
При этом квантовое число L получается алгебраич. сложением проекций MLi орбитальных моментов всех атомов,

а полный электронный спин M. получается как векторная сумма спинов атомов

Напр., если молекула HCN образована из атомов И, С,
N в их основных состояниях 2Sg, 3Pg, 4Su соответственно, то L
= 1 или 0 и S = 3, 2.2, 1, 1, 0 и для HCN получаются след. уровни: 1S,
1P,
по два уровня типа 3S, 3P,
5S, 5P,
по одному уровню 7S и 7П. Уровни HCN можно получить
также из уровней H и CN.
Модели о. а. и р. а. позволяют определить кол-во
электронных уровней разл. типов симметрии, но не дают надёжных сведений относительно
их энергии. Более полную информацию о расположении уровней и их устойчивости
дают молекулярные орбитали.
Электронные уровни энергии расщепляются за счёт
спин-орбитального взаимодействия на т. н. мультиплет-иые уровни (см. Мультиплетность). В случае нормальной связи это расщепление равно:

константа А спин-орбитального взаимодействия
быстро растёт с ростом зарядов ядер атомов, составляющих M. Квантовые числа
L и S теряют смысл хороших квантовых чисел, а расщеплённые подуровни
теперь характеризуются значениями квантового числа W = = L + S
проекции полного электронного угл. момента на ось M. Напр., уровень 3П
линейной M. за счёт спин-орбитального взаимодействия расщепляется на подуровни
S + , S-, П, D, соответствующие значениям
W = 0,0, l, 2. Константа А составляет от неск. см-1 для
лёгких M. до неск. сотен см''1 для тяжёлых M.
Колебат. структура синглетных электронных состояний M. описывается
ф-лами (13) - (15), в к-рых, однако, следует учесть зависимость частот колебаний
и постоянных ангармоничности от электронного состояния. Они также описывают
уровни невырожденных колебаний в вырожденных электронных состояниях или же уровни
вырожденных колебаний в невырожденных электронных состояниях. Качественно новые
эффекты возникают в вырожденных электронных состояниях при возбуждении вырожденных
колебаний, в основном за счёт взаимодействия колебат. угловых моментов вырожденных
колебаний с электронным орбитальным угл. моментом.
Для симметричного волчка или линейной молекулы
электронно-колебательные (вибронные) уровни энергии можно классифицировать по
значениям квантового числа К = L + l проекции вибронного
угл. момента на ось симметрии M. Электронно-колебат. взаимодействие снимает
вырождение по L и l, и вибронные уровни энергии расщепляются. В
M. типа симметричного и сферич. волчков линейные члены разложения электронного
гамильтониана по координатам вырожденных колебаний не равны нулю, расщепление
виб-ронных уровней в этом случае наз. линейным эффектом Яна - Теллера (см. Вибронное
взаимодействие). Энергия расщеплённых подуровней даётся ф-лой:
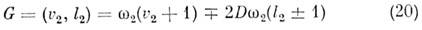
при малых величинах параметра Яна - Теллера D. Для линейных M. линейные члены разложения электронного гамильтониана равны
нулю и расщепление описывают квадратичные члены разложения (эффект Рен-пера).
В реальных M. эффекты Яна - Теллера и Рен-пера следует учитывать совместно с
ангармонизмом и спин-орбитальным взаимодействием.
Определяющую роль в формировании вра-щат. структуры вырожденных
электронных и вибронных состояний играют взаимодействия вращат. углового момента
с электронным спином и орбитальным (или вибронным) угл. моментом. В общем случае
многоатомной M. учёт всех этих взаимодействий
довольно сложен. Для двухатомных M. различают неск. предельных случаев связи
угл. моментов, получивших назв. случаев Хунда. В случае а предполагается
наличие сильного спин-орбитального взаимодействия, что справедливо для достаточно
тяжёлых M. В этом случае сначала учитывают связь L и S,
а затем - связь суммарного момента j = L + S
с R. В случаях Хунда b спин-орбитальное взаимодействие
предполагается очень слабым (справедливо для лёгких M. и для всех S-состояний):
сначала учитывают связь R с L, а затем
N=R+L с S и получают
J. Существуют и др. случаи Хунда. Ниже приведены вращат.
энергии для M. типа жёсткого волчка для случаев а, b, с и d.

Взаимодействие вращат. углового момента с электронными
моментами приводит к снятию вырождения, указанного в последнем столбце этой
табл. В 1P-состояниях
взаимодействие типа L2J2 приводит
к эффекту L-удвоения с величиной Dv = qeJ(J + 1), где qe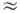 2В2е
/ve, a ve - разность энергии и ближайшего
1S-состояния.
2В2е
/ve, a ve - разность энергии и ближайшего
1S-состояния.
Каждый уровень энергии молекулы может иметь ядерную
сверхтонкую структуру (CTC), обусловленную наличием у ядер электрич. и магн.
моментов. В электронном 1S-состоянии ядерная CTC уровней формируется
в результате: 1) электростатич. взаимодействия электрич. квадрупольного момента
ядра с электрич. полем M. (квадрупольное взаимодействие или квадрупольная связь);
2) взаимодействия магн. дипольного момента ядра с магн. полем, возникающим при
вращении M. (ядерное спин-вращательное взаимодействие); 3) взаимодействия магн.
моментов разл. ядер между собой (ядерные спин-спиновые взаимодействия).
Обычно квадрупольное взаимодействие даёт осн.
вклад в CTC, но оно имеет место только для ядер со спином l > 1/2
(напр., D, 14N, Cl, Br, I). В простейшем случае одиночного квадрупольного
ядра в двухатомной M. энергия квадрупольного взаимодействия описывается ф-лой
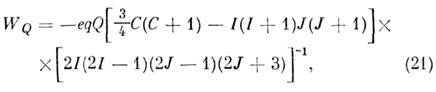
где е - заряд электрона, q - градиент
электрич. ноля, Q - квадрупольный момент ядра, J - вращат. квантовое
число, I - спин ядра,
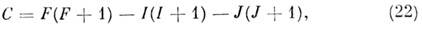
a F - квантовое число полного угл. момента
F= =J + I, получающее значения
F = J + 1, J + I - 1, J + I - 2, .., J
- I. Число J теряет смысл хорошего квантового числа, и уровни
CTC классифицируются по значениям F. Напр., вращат. уровень с J
= 1 в случае ядра со спином I = 5/2 (ядра Al, I
и др.) расщепляется на три подуровня с F = 5/2,
7/2 и 3/2 с энергией WQ
= +4еqQ/25, - egQ/20 и - 7eqQ/50. Константа
квадрупольпой связи eqQ зависит и от типа ядра и от молекулярного окружения
и изменяется в широком интервале.
Квадрупольная CTC обычно наблюдается в спектрах
высокого разрешения. Спин-вращательные и спин-спиновые взаимодействия дают небольшой
вклад в CTC и имеют место для всех ядер
со спином I >= 1/2 (I = 1/2
для H, F и др.). Расщепления вращат. уровней за счёт этих взаимодействий
составляют обычно не более 100 кГц и наблюдаются только на уникальных установках
(пучковые мазеры, электрич. резонанс в пучке и Др.). Эксперим. данные по константам
квадруполь-ной связи и спин-вращательного взаимодействия дают ценную информацию
об электронном строении M., а константы спин-спиновых взаимодействий зависят
только от гсом. параметров M.
В вырожденных электронных состояниях важное значение
имеют взаимодействия электронного спина с ядерными спинами, энергия к-рых в
gemБ/gI mЯ раз
больше энергии чисто ядерных спин-спиновых взаимодействий, где gc
и gI - электронный и ядерный g-факторы, mБ
- магнетон Бора, mЯ - ядерный магнетон. Электрон-ядерные
спин-спиновые взаимодействия бывают двух видов: 1) классич. диполь-дипольное
взаимодействие (анизотропное), энергия к-рого в общем случае произвольной M.
определяется тензором второго ранга с 9 компонентами; 2) не имеющее классич.
аналога изотропное контактное взаимодействие Ферми aSI, обусловленное
наличием электронной спиновой плотности в место расположения ядра. В отличие
от анизотропного спин-спинового взаимодействия контактное взаимодействие имеет
место только в состояниях с L = 0, аналогичных s-состояниям атомов,
т. к. только атомные s-орбитали создают спиновую плотность в месте расположения
ядра. Константы обоих видов взаимодействий зависят от электронной плотности
M. p дают ценную информацию об электронных волновых функциях M.
Все физ. и хим. свойства молекулы так или иначе связаны
с системой уровней энергии молекулы и с переходами между ними под действием внеш.
возмущений.
Молекула как система положит. и отрицат. зарядов характеризуется опре-дел. расположением
зарядов, т. с. обладает электрич. дипольным, квадрупольным и т. д. моментами.
Определяет электрич. свойства M. её дипольный момент m:

где ei, ri - заряд и радиус-вектор i-й частицы, входящей в M. Вектор m
можно разложить на составляющие ma, mb и mс
по направлениям гл. осей инерции a, b и с.
Асимметрия распределения заряда r характеризуется квадрупольным моментом,
к-рый для M. определяется так же, как и для ядра:
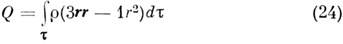
или
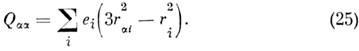
Дипольный момент M. определяет интенсивности
линий в спектрах поглощения и испускания, различные электрич. явления в газах
(электрич. потери, отклонения пучков M. в неоднородных электрич. полях и т.
д.). Электрич. дипольный момент M. d зависит от нормальных
колебат. координат qk, и при малых смещениях ядер из положения
равновесия его можно разложить в ряд Тейлора по степеням qk. Первый
не зависящий от qk член mе этого ряда наз. постоянным дипольным моментом M. Не все M. имеют пост. дипольный
момент. Он отличен от нуля, если по крайней мере одна из компонент электрич.
дипольного момента принадлежит к полносимметричному типу симметрии группы симметрии
M. Если m 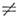 0, то M. наз. полярной, a M. с m = 0 наз. неполярными. К полярным, напр.,
относятся H2O, NH3, к неполярным - CH4, BF3,
CO2. В M. NH3 дипольный момент me
направлен по оси симметрии C3, в H2O
mеа - по оси C2, a meb - перпендикулярно оси C2.
0, то M. наз. полярной, a M. с m = 0 наз. неполярными. К полярным, напр.,
относятся H2O, NH3, к неполярным - CH4, BF3,
CO2. В M. NH3 дипольный момент me
направлен по оси симметрии C3, в H2O
mеа - по оси C2, a meb - перпендикулярно оси C2.
Наиб. прецизионный метод определения me состоит в измерении расщепления уровней энергии и соответствующих спектральных
линий при наложении на M. внеш. электрич. поля (Штарка эффект ).В общем
случае вращат. уровень с заданными J, К расщепляется в электрич.
поле на (2J + 1) компонентов, т. к. в электрич. поле энергия уровня зависит
ещё и от магн. квантового числа т, т. е. квантового числа проекции угл.
момента J на направление поля: т = -J, -J +1, ..,
+ J. Обычно напряженность внеш. электрич. поля E выбирают так,
чтобы энергия взаимодействия M. с полем (-mE)была значительно
меньше энергии вращат. перехода. Тогда величина штарковского расщепления уровня
энергии зависит от E или линейно (эффект Штарка 1-го порядка), или квадратично
(эффект Штарка 2-го порядка); в общем случае она выражается как аЕ +
bЕ2+... . Если поле направлено по оси z, фиксированной
в пространстве, то энергия взаимодействия M. с полем будет равна -mzEz, где mz - проекция m на ось z.
Электрич. дипольный момент обычно измеряют в
единицах Дебая: 1Д = b10-18 СГСЕ. Для полярных M. он составляет
от долей до неск. Д (напр., для SO2 me = meb
= 1,58Д, для OCS me = 0,7124Д, для KCl me
= 10,27 Д, для NH3 me = 1,49 Д). Константа
Штарка mE = 0,50344 (МГц/Д).(В/см). Поэтому при
точности измерений частот ок. 10 кГц штарковское расщепление в полях 102-103
В/см достаточно велико и поддаётся весьма точному измерению. Обычно дипольный
момент M. измеряется с точностью до 0,01 Д, но в спец. экспериментах достигнута
точность вплоть до 10-7Д.
В состоянии с орбитальным моментом L электрона M. имеет орбитальный магн. момент

а в состоянии со спином S - спиновой
магн. момент

где mБ - магнетон Бора, gs
- спиновый g-фактор свободного электрона (см. Ланде множитель; )знак
минус указывает на то, что магн. и механич. моменты направлены антипараллельно.
В 1S-состоянии
(L= S=0) электронный магн. момент отсутствует, но M. может иметь
небольшой магн. момент, к-рый возникает из-за вращения M. При вращении M. происходит
слабое перемешивание электронной волновой функции основного состояния с волновыми
функциями возбуждённых "парамагнитных" состояний. Кроме того, вращение
ядер само по себе создаёт магн. момент. При этом возникает т. н. вращательный
магн. момент с компонентами по гл. осям инерции в виде:
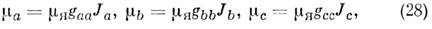
где mЯ - ядерный
магнетон и gaa, gbb, gcc - компоненты
тензора вращат. g-фактора, определяемые для основного состояния по ф-ле:
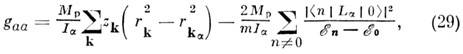
где Mp - масса протона, Ia
- гл. моменты инерции, т - масса электрона, zk
- заряд k-го ядра, rk - его радиус-вектор,
rka
- проекция rk на ось a,
a суммирование по n проводится по всем возбуждённым электронным состояниям,
связанным с основным состоянием матричными элементами орбитального момента:
первый член даёт вклад ядер, второй - вклад электронов. Очевидно, что вращат.
магн. момент намного (в 103-104 раз) меньше орбитального
и спинового магн. моментов. Энергия взаимодействия магн. момента m
с внеш. магн. полем H, направленным по оси z лабораторной
системы координат, даётся ф-лой:

где
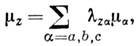
lza
- направляющая косинусов компонентов ma
в гл. осях инерции относительно оси z. Можно показать, что оператор H имеет
диагональные матричные элементы в состоянии |J, т, Г >
типа симметрии Г, если тип симметрии JM содержится в симметричном
произведении [Г2], т. е. если
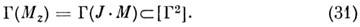
T. к. Mz всегда относится к
полносимметричному типу симметрии и [Г2] всегда содержит полносимметричный
тип, условие (30) фактически не ограничивает класс состояний, в к-рых H имеет
диагональные элементы. T. о., расщепление уровней энергии во внеш. магн. поле
(Зеемана эффект)происходит для всех M. уже в первом приближении, т.
е. наличие линейного по нолю эффекта Зеемана ничем не ограничено. Величина линейного
зеемановского расщепления для жёсткого асимметричного волчка даётся ф-лой:

где
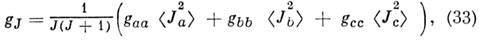
ср. значение <J2a>
определяют численно. Для симметричного волчка
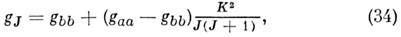
а для линейной M. gJ = g, т. е. не зависит от J. Обычно расщепления уровней энергии за счёт
вращат. эффекта Зеемана малы и для их точного измерения используют магн. поля
~ (20-50).103 Гс. Следует отметить, что в таких сильных
полях, вследствие магн. восприимчивости c, в M. возникает ещё и наведённый
магн. момент, к-рый также вносит вклад в зеемановское расщепление.
По величине зеемановского расщепления уровней
энергии определяются вращат. g-факторы и компоненты тензора c, а
из них вычисляются электрич. квадру-польные моменты M. по ф-лам:
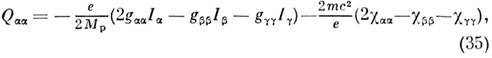
где
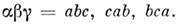
В вырожденных электронных состояниях зееманов-ская
энергия определяется также ф-лой (32), в к-рой, однако, следует заменить ядерный
магнетон mЯ на магнетон Бора mБ и учесть, что
g -факторы зависят от типа состояния и величины взаимодействия угл. моментов.
Напр., в случае Хунда а в П- и D-состояниях двухатомной M. электронный
магн. момент вдоль оси M. равен:
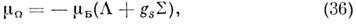
а электронный g-фактор
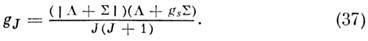
T. к. mБ/mЯ ~ 103, зеемановские расщепления вращат. уровней энергии вырожденных электронных состояний наблюдаются и точно измеряются уже в полях в неск. десятков Гс. Поэтому методы, основанные на эффекте Зеемана (зеемановская модуляция в микроволновой спектроскопии и лазерный магн. резонанс), используются для изучения радикалов и ионов с открытыми электронными оболочками.
Согласно Максвелла - Больцмана распределению, при
тепловом равновесии число M. Nn в
состоянии с энергией 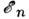 и статистическим весом gn пропорц. величине
и статистическим весом gn пропорц. величине
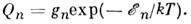
При T 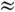 300
К (Tk
300
К (Tk 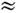 200
см-1) подавляющее большинство M. находится в основном электронном
состоянии и распределено по вращат. уровням основного ко-лебат. состояния, а
их небольшая часть - по уровням НЧ-колебаний (т. е. по уровням с энергией до
500- 700 см-1). Если M. не содержит ядер с отличным от нуля спином,
то величина gn равна числу состояний с различными магн. квантовыми
числами m, T. е. gJ = = 2J + 1. В случае жёсткого
сферич. волчка вращат. уровни вырождены ещё и по квантовому числу К проекции
вращательного угл. момента J по одной из осей M. и gJ =
(2J + 1)2. Если M. содержит ядра X, Y,... с ненулевыми
спинами IX, IY, ..., но не содержит тождеств. ядер
(напр., HCl, HCN), то статистич. веc содержит множитель (2IX
+1)(2IY + 1)..., одинаковый для всех вращат. уровней,
к-рый не влияет на распределение M. по вращат. уровням. Для M., содержащих тождеств.
ядра, статистич. веса уровней с различными J, К будут иметь разл.
спиновые множители. Напр., отношение спиновых статистич. весов симметричных
(J чётное) и антисимметричных (J нечётное) вращат. уровней двухатомной
M., состоящей из одинаковых ядер со спином I, равно (I+1)/I,
если I целое (I = 1, 2, 3...), или I/(I+1), если
I полуцелое (I = 1/2, 3/2,...);
если I = 0, то антисимметричные уровни отсутствуют.
200
см-1) подавляющее большинство M. находится в основном электронном
состоянии и распределено по вращат. уровням основного ко-лебат. состояния, а
их небольшая часть - по уровням НЧ-колебаний (т. е. по уровням с энергией до
500- 700 см-1). Если M. не содержит ядер с отличным от нуля спином,
то величина gn равна числу состояний с различными магн. квантовыми
числами m, T. е. gJ = = 2J + 1. В случае жёсткого
сферич. волчка вращат. уровни вырождены ещё и по квантовому числу К проекции
вращательного угл. момента J по одной из осей M. и gJ =
(2J + 1)2. Если M. содержит ядра X, Y,... с ненулевыми
спинами IX, IY, ..., но не содержит тождеств. ядер
(напр., HCl, HCN), то статистич. веc содержит множитель (2IX
+1)(2IY + 1)..., одинаковый для всех вращат. уровней,
к-рый не влияет на распределение M. по вращат. уровням. Для M., содержащих тождеств.
ядра, статистич. веса уровней с различными J, К будут иметь разл.
спиновые множители. Напр., отношение спиновых статистич. весов симметричных
(J чётное) и антисимметричных (J нечётное) вращат. уровней двухатомной
M., состоящей из одинаковых ядер со спином I, равно (I+1)/I,
если I целое (I = 1, 2, 3...), или I/(I+1), если
I полуцелое (I = 1/2, 3/2,...);
если I = 0, то антисимметричные уровни отсутствуют.
Полное число M. в данном объёме пропорц. суммe
величин Qn по всем состояниям M., т. е.
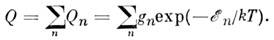
Величина Q наз. статистической суммой
или суммой по состояниям, через неё могут быть выражены все термодинамич. функции
идеального газа, причём учитываются все степени свободы M., включая и её поступат.
движение. Если не учитывать взаимодействие между видами внутр. движений M.,
то величину Q можно представить в виде произведения поступательной (Qt), вращательной (Qr), колебательной (Qu)и электронной (Qe)статистич. сумм:
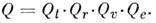
Статистич. сумма поступат. движения M. для объёма
газа V и температуры T равна
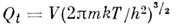
(т - масса M.). Вращат. статистич. сумма
для жёсткой двухатомной или линейной многоатомной M. при kcB <<
kT (без учёта ядерных спиновых статистич. весов)
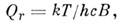
для M. типа жёсткого симметричного волчка
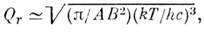
а для жёсткого асимметричного волчка
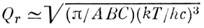
(А, В, С - вращат. постоянные). Колебат.
статистич. сумма Qu
в гармонич. приближении выражается как произведение величин
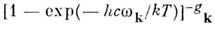
для каждого нормального колебания с частотой
wk
и кратностью вырождения gk. Если все возбуждённые электронные
состояния M. сильно удалены от основного состояния (что справедливо для большинства
устойчивых M.), можно положить Qe 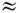 1.
1.
T. о., если известны частоты нормальных колебаний
и вращат. постоянные M., то можно найти полную статистич.
сумму Q, а затем вычислить термодинамич. функции газа. В частности, теплоёмкость
Ср одного моля газа при пост. давлении определяется по ф-ле
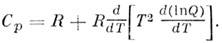

M. P. Алиев
|
|