Симметрия молекул играет фундаментальную роль в молекулярной спектроскопии, позволяет проводить классификацию уровней энергии молекул, определить отбора правила для молекул, существенно упростить аналитич. и численные расчёты внутр. энергий и вероятностей переходов молекул.
В наиб. общем виде С. м. определяется как группа преобразований, оставляющих полный гамильтониан молекулы инвариантным, и состоит из следующих операций:
а) все перестановки координат и спинов электронов;
б) любое вращение координат и спинов всех частиц (электронов и ядер) вокруг любой оси (оси симметрии), проходящей через центр масс молекулы;
в) любая трансляция молекулы в пространстве;
г) обращение знака всех линейных и угл. моментов, эквивалентное обращению времени;
д) одноврем. инверсия координат всех частиц в центре масс;
е) любая перестановка координат и спинов тождественных ядер.
Каждый из наборов этих операций составляет отдельную группу, а каждая группа симметрии гамильтониана представляет собой прямое произведение всех этих групп. При решении конкретных задач используют не все перечисленные группы. Группа (а) используется только в связи с Паули принципом ,согласно к-рому волновая функция электрона антисимметрична относительно любой перестановки электронов; группа (б) отражает закон сохранения для полного угл. момента молекулы; группа (в) для изолиров. молекулы несущественна, т. к. трансляции молекулы не влияют на волновые функции, описывающие внутр. состояние молекулы; инвариантность гамильтониана относительно групп (г) и (д) показывает, что он может содержать только чётные степени угл. моментов и пространственных декартовых координат частиц.
Для молекулы наиб. важны группа (а) и прямое произведение групп (д) п (е), к-рое представляет собой т. н. перестановочно-инверсионную (ПИ) группу С. м. ПИ-грунпы введены в теорию С. м. X. К. Лонге-Хиггинсом (Н. Ch. Longuet-Higgins) в 1963. Частным случаем ПИ-групп являются точечные группы С. м. Группы (б), (в) и (г) лишь накладывают на гамильтониан молекулы определённые условия, к-рые учитываются при решении конкретных задач. Для групп С. м. применяют обозначения, заимствованные из кристаллографии (см. Симметрия кристаллов).
ПИ-группа симметрии молекул представляет собой прямое произведение групп перестановок тождественных ядзр (Е,Р)на группу инверсии (Е, Е*), где Е - идентичная операция, Е* - инверсия, Р - перестановки. ПИ-груипа состоит из перестановок Р тождественных ядер, перестановок с инверсией Р* = РЕ* = Е*Р и идентичной операции Е; просто инверсия Е может не быть элементом ПИ-группы. Для молекул, содержащих много тождественных ядер, размерность ПИ-группы может быть очень большой, т. к. она определяется только хим. ф-лой молекулы. Напр., полная ПИ-группа молекулы С6Н5С1 состоит из 2*6!*5!*1! = 2*720*120*1 = 172 800 операций, и очевидно, что такая группа для практич. целей бесполезна. Лонго-Хиггинс предложил постулат, согласно к-рому из полной группы выбирается подгруппа, элементы к-рой соответствуют физически возможным операциям. Физически невозможными считаются операции, отвечающие разрыву хим. связей, и операции переходов между равновесными конфигурациями молекул, разделёнными высокими потенциальными барьерами. После исключения таких физически невозможных операций получается ПИ-группа обычно небольшой размерности, к-рая и используется при классификации уровней энергии молекулы. Напр., для С6Н5С1 такая подгруппа состоит всего из 4 элементов и изоморфна точечной группе симметрии С2v (см. ниже).
В нек-рых случаях полная ПИ-группа состоит только из физически возможных
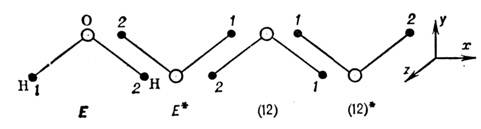
операций. Напр., ПИ-группа молекулы Н2О состоит из 4 операций:
Е, перестановки (12), Е* и (12)*, к-рые графически можно представить
в виде:

где каждый вид молекулы получен из первого с помощью операции, указанной
под ним. Эта ПИ-группа изоморфна точечной группе С2v, состоящей
из чисто геом. операций вращения С2 вокруг биссектрисы валентного
угла H1OH2 на 180°, отражения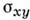 на плоскости молекулы и отражения
на плоскости молекулы и отражения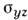 на плоскости, проходящей через ось С2 и перпендикулярной плоскости
молекулы. Изоморфизм выражается следующими тождествами:
на плоскости, проходящей через ось С2 и перпендикулярной плоскости
молекулы. Изоморфизм выражается следующими тождествами: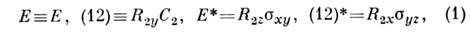 где R2x, R2y, R2z - операции вращения
на 180° вокруг осей х, у, z соответственно.
где R2x, R2y, R2z - операции вращения
на 180° вокруг осей х, у, z соответственно.
В случае Н2О все операции ПИ-группы физически осуществимы,
т. к. молекула Н2О имеет только одну равновесную конфигурацию.
Если молекула имеет неск. равновесных конфигураций, то ПИ-группа имеет
подгруппу, к-рая изоморфна точечной группе симметрии одной из равновесных
конфигураций. Напр., полная ПИ-группа молекулы NH3 состоит из
элементов:
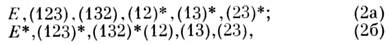
где (123) обозначает циклич. перестановку трёх протонов, (12), (13),
(23) - парные перестановки, а (...)*- парные перестановки с последующей
инверсией. ПИ-группа изоморфна точечной группе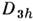 ,
но элементы в (2а) [а также и в (2б)] составляют подгруппу, к-рая изоморфна
точечной группе
,
но элементы в (2а) [а также и в (2б)] составляют подгруппу, к-рая изоморфна
точечной группе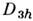 .
Подгруппа (2а) описывает также геом. симметрию пирамидальной равновесной
конфигурации NH3, подгруппа (2б) описывает геом. симметрию др.
пирамидальной равновесной конфигурации NH3, получаемой от первой
при инверсии. Поэтому если инверсионный потенциальный барьер невысок и
туннелирование через него наблюдается в виде туннельного расщепления ровибронных
уровней (см. Молекула ),то следует использовать для классификации
уровней энергии ПИ-группу или точечную группу D3h; если
туннельное расщепление не наблюдается, то можно использовать группу C3v. Для
NH3 инверсионный барьер составляет ок. 2000 см-1
(в единицах частоты перехода) и инверсионное туннельное расщепление уровней,
равное в основном колебат. состоянии 0,8 см-1, в первом возбуждённом
колебат. состоянии 36 см-1, во 2-м - 285 см-1, легко
наблюдается. Поэтому для NH3 используют группу D3h. Для
молекул РН3, AsH3, SbH3 инверсионное расщепление
в низких колебат. состояниях не наблюдается, и для них используется группа
С3v. Интересен также пример молекулы N2H4
(гидразин), равновесная конфигурация к-рой имеет низкую геом. симметрию
С2, но, т. к. инверсия на обоих атомах азота и внутр. вращение
вокруг связи N - N имеют достаточно низкие барьеры, ПИ-группа состоит из
16 физически возможных операций и изоморфна точечной группе D4h:
фактически происходит туннелирование гидразина между 8 эквивалентными равновесными
конфигурациями и уровни жёсткой конфигурации с симметрией С2
расщепляются в соответствии с корреляцией между типами симметрии групп
С2
и О4h.
.
Подгруппа (2а) описывает также геом. симметрию пирамидальной равновесной
конфигурации NH3, подгруппа (2б) описывает геом. симметрию др.
пирамидальной равновесной конфигурации NH3, получаемой от первой
при инверсии. Поэтому если инверсионный потенциальный барьер невысок и
туннелирование через него наблюдается в виде туннельного расщепления ровибронных
уровней (см. Молекула ),то следует использовать для классификации
уровней энергии ПИ-группу или точечную группу D3h; если
туннельное расщепление не наблюдается, то можно использовать группу C3v. Для
NH3 инверсионный барьер составляет ок. 2000 см-1
(в единицах частоты перехода) и инверсионное туннельное расщепление уровней,
равное в основном колебат. состоянии 0,8 см-1, в первом возбуждённом
колебат. состоянии 36 см-1, во 2-м - 285 см-1, легко
наблюдается. Поэтому для NH3 используют группу D3h. Для
молекул РН3, AsH3, SbH3 инверсионное расщепление
в низких колебат. состояниях не наблюдается, и для них используется группа
С3v. Интересен также пример молекулы N2H4
(гидразин), равновесная конфигурация к-рой имеет низкую геом. симметрию
С2, но, т. к. инверсия на обоих атомах азота и внутр. вращение
вокруг связи N - N имеют достаточно низкие барьеры, ПИ-группа состоит из
16 физически возможных операций и изоморфна точечной группе D4h:
фактически происходит туннелирование гидразина между 8 эквивалентными равновесными
конфигурациями и уровни жёсткой конфигурации с симметрией С2
расщепляются в соответствии с корреляцией между типами симметрии групп
С2
и О4h.
Точечные группы симметрии молекул. Как было указано выше, симметрия
равновесной конфигурации молекулы описывается точечной группой, к-рая может
быть изоморфна подгруппе ПИ-группы или самой ПИ-группе. Точечные группы
состоят из чисто геом. операций поворотов и отражений, переводящих равновесную
конфигурацию молекулы в саму себя. Точечными эти группы наз. потому, что
по крайней мере одна точка молекулы при операциях точечной группы симметрии
остаётся неподвижной. Элементами таких групп кроме идентичной операции
Е могут быть: поворот Сп вокруг оси симметрии n-го
порядка, отражение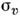 на плоскости, содержащей ось Сп, отражение
на плоскости, содержащей ось Сп, отражение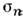 на плоскости, перпендикулярной к оси Сп, и инверсия i (не
следует путать i с E*!). Напр., группа С2v состоит из
Е, поворота вокруг оси С2 на 180° и двух отражений
на взаимно перпендикулярных плоскостях с осью пересечения на С2; группа
С3v состоит из Е, поворотов. С3 и
на плоскости, перпендикулярной к оси Сп, и инверсия i (не
следует путать i с E*!). Напр., группа С2v состоит из
Е, поворота вокруг оси С2 на 180° и двух отражений
на взаимно перпендикулярных плоскостях с осью пересечения на С2; группа
С3v состоит из Е, поворотов. С3 и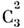 вокруг
оси С3 на 120° и 240°, трёх отражений
вокруг
оси С3 на 120° и 240°, трёх отражений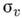 на плоскостях, проходящих через ось С3. Осн. характеристиками
точечной группы (как и ПИ-группы) являются их неприводимые представления
(см. Представление группы ),наз. также типами симметрии, к-рые определяют
свойства преобразования волновых функций при операциях точечной группы. Типы
симметрии обозначают буквами А, В, Е, F (или Т)с индексами
на плоскостях, проходящих через ось С3. Осн. характеристиками
точечной группы (как и ПИ-группы) являются их неприводимые представления
(см. Представление группы ),наз. также типами симметрии, к-рые определяют
свойства преобразования волновых функций при операциях точечной группы. Типы
симметрии обозначают буквами А, В, Е, F (или Т)с индексами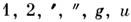 . Буквами А я В обозначают одномерные неприводимые представления,
или невырожденные типы симметрии. Так,
. Буквами А я В обозначают одномерные неприводимые представления,
или невырожденные типы симметрии. Так,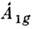 означает, что волновая функция типа
означает, что волновая функция типа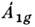 полносимметрична относительно всех операций точечной группы. Если волновая
функция симметрична относительно операции поворота вокруг оси, она обозначается
буквой А, а если антисимметрична,- буквой В. Индексы 1 и
2 указывают симметричность и антисимметричность функции относительно отражения
на плоскости
полносимметрична относительно всех операций точечной группы. Если волновая
функция симметрична относительно операции поворота вокруг оси, она обозначается
буквой А, а если антисимметрична,- буквой В. Индексы 1 и
2 указывают симметричность и антисимметричность функции относительно отражения
на плоскости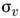 ,
верхние индексы ' и
,
верхние индексы ' и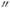 - относительно отражения на плоскости
- относительно отражения на плоскости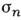 .
Буквой Е (от нем. entartet - вырожденный) обозначают дважды вырожденный,
а буквой F (или Т)трижды вырожденный тип симметрии. Напр.,
точечная группа Td молекулы СН4 состоит из
24 операций и имеет типы симметрии A1, А2, Е,
F1 и F2. ПИ-группа СН4 состоит
из 2*4! = 48 операций и изоморфна прямому произведению
.
Буквой Е (от нем. entartet - вырожденный) обозначают дважды вырожденный,
а буквой F (или Т)трижды вырожденный тип симметрии. Напр.,
точечная группа Td молекулы СН4 состоит из
24 операций и имеет типы симметрии A1, А2, Е,
F1 и F2. ПИ-группа СН4 состоит
из 2*4! = 48 операций и изоморфна прямому произведению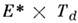 , но инверсия связана с преодолением очень высокого барьера. Поэтому уровни
типа A1, А2 и т. д. СН4 фактически
состоят из двух инверсионных подуровней с одинаковой энергией, обозначаемых
верхними индексами «+» и «-», к-рые указывают симметрию и антисимметрию
относительно пространственной инверсии:
, но инверсия связана с преодолением очень высокого барьера. Поэтому уровни
типа A1, А2 и т. д. СН4 фактически
состоят из двух инверсионных подуровней с одинаковой энергией, обозначаемых
верхними индексами «+» и «-», к-рые указывают симметрию и антисимметрию
относительно пространственной инверсии: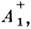
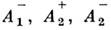 и т. д. На практике часто используются характеры неприводимых представлений
точечных групп, таблицы к-рых приводятся обычно в литературе по теории
групп и по молекулярной спектроскопии.
и т. д. На практике часто используются характеры неприводимых представлений
точечных групп, таблицы к-рых приводятся обычно в литературе по теории
групп и по молекулярной спектроскопии.
Классификация нормальных колебаний молекулы по типам симметрии. Молекула,
состоящая из N атомов, имеет 3N степеней свободы (N
- число атомов в молекуле), из к-рых 3N - 6 связаны с относит. движением
атомов - их колебаниями, а остальные 6 относятся к вращениям и поступат.
движениям молекулы в целом. Для симметричных молекул смещения атомов в
данном колебании или вращении (трансляции) относятся к определённому типу
симметрии точечной группы или ПИ-группы. Число степеней свободы типа симметрии
Гg определяется по ф-ле
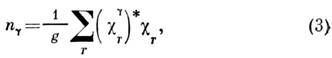
где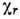 - характер приводимого представления для операции r (т. е. представления
размерности 3N X 3N, по к-рому преобразуются произвольно
выбранные смещения атомов),
- характер приводимого представления для операции r (т. е. представления
размерности 3N X 3N, по к-рому преобразуются произвольно
выбранные смещения атомов),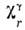 - характер неприводимого
- характер неприводимого
представления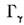 ,
индекс «*» указывает на комплексное сопряжение, g - порядок точечной
группы. Характеры
,
индекс «*» указывает на комплексное сопряжение, g - порядок точечной
группы. Характеры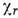 определяются по поведению декартовых координат атомов при операциях точечной
группы. При идентичной операции Е все координаты всех атомов остаются
неизменными, поэтому
определяются по поведению декартовых координат атомов при операциях точечной
группы. При идентичной операции Е все координаты всех атомов остаются
неизменными, поэтому . Если при операции r атомы меняются местами, то их вклад в
. Если при операции r атомы меняются местами, то их вклад в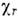 равен нулю. Напр., для
равен нулю. Напр., для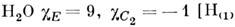 и Н(2) меняются местами, y(0) остаётся неизменной, а
х(0)и z(0)меняют знак],
и Н(2) меняются местами, y(0) остаётся неизменной, а
х(0)и z(0)меняют знак],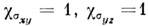 . Характеры
. Характеры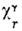 приведены в табл.:
приведены в табл.:
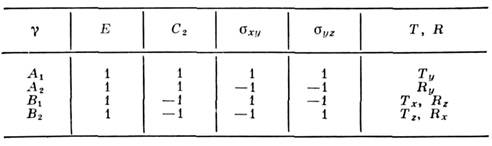
В последнем столбце даны типы симметрии вращений и трансляций (относительно
осей х, у, z)молекулы в целом. Тогда из (3) следует
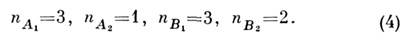
За вычетом трёх вращений и трёх трансляций получим два колебания типа
А1 и одно колебание типа B1, к-рые обозначаются также
символами vl, v2(A1)и v3(В1). Осн. колебат. состояние всегда относится к типу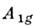 , первое возбуждённое состояние колебания типа
, первое возбуждённое состояние колебания типа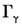 принадлежит к тому же типу симметрии
принадлежит к тому же типу симметрии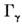 ,
типы симметрии более высоких возбуждённых состояний определяются из прямых
произведений симметризованных степеней типов симметрии возбуждённых колебаний.
Если в данном состоянии молекулы возбуждено п колебаний типа
,
типы симметрии более высоких возбуждённых состояний определяются из прямых
произведений симметризованных степеней типов симметрии возбуждённых колебаний.
Если в данном состоянии молекулы возбуждено п колебаний типа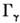 ,
т колебаний типа
,
т колебаний типа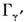 и т. д., то тип симметрии такого состояния определяется из прямого произведения
симметризов. степеней
и т. д., то тип симметрии такого состояния определяется из прямого произведения
симметризов. степеней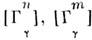
и т. д. Напр., тип симметрии состояния с возбуждением одного колебания
v3(E)и двух квантов колебания v1(E)молекулы NH3
будет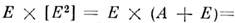
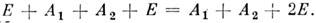
Модельные симметрии. Если молекула не содержит тождественных
ядер, то её ПИ-группа сводится к группе инверсий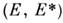 : симметричные и антисимметричные состояния такой молекулы (напр., CHFClBr)
могут отличаться по энергии только за счёт слабых электронно-ядерных взаимодействий.
Однако и для таких молекул при решении конкретных модельных задач часто
оказываются полезными группы симметрии более высоких порядков. Напр., в
теории вращат. спектров в качестве нулевого приближения используется модель
жёсткого волчка, к-рой присуща своя симметрия. Гамильтониан молекулы типа
жёсткого асимметричного волчка
: симметричные и антисимметричные состояния такой молекулы (напр., CHFClBr)
могут отличаться по энергии только за счёт слабых электронно-ядерных взаимодействий.
Однако и для таких молекул при решении конкретных модельных задач часто
оказываются полезными группы симметрии более высоких порядков. Напр., в
теории вращат. спектров в качестве нулевого приближения используется модель
жёсткого волчка, к-рой присуща своя симметрия. Гамильтониан молекулы типа
жёсткого асимметричного волчка
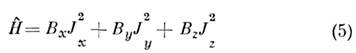
инвариантен относительно поворотов на 180° вокруг гл. осей инерции х,
у, z (Jx, Jy, Jz - соответствующие
моменты), т. е. относительно операций точечной группы D2 4-го
порядка. Учёт этой симметрии даёт полезный способ классификации вращат.
уровней асимметричного волчка и позволяет разложить матрицу вращат. энергии
на 4 блока. Гамильтониан молекулы типа симметричного волчка, получаемый
из (5) при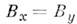 , инвариантен относительно операций группы
, инвариантен относительно операций группы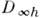 любых поворотов вокруг оси z и отражения на плоскости
любых поворотов вокруг оси z и отражения на плоскости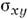 . Эта группа позволяет классифицировать вращат. уровни энергии молекул
типа симметричного волчка по квантовому числу К. Модельная симметрия
часто используется и для нежёстких молекул, когда нек-рые атомные группы
в молекуле имеют достаточно высокую симметрию, хотя сама молекула высокой
симметрии не имеет. Напр., если молекула содержит СН3-группу,
то при изучении внутр. вращения такой группы используется точечная группа
C3v. В частности, туннелирование группы СН3 в периодич. потенциальной
яме с тремя минимумами приводит к известному дублетному A- E-расщеплению
уровней по типам симметрии точечной группы
C3v. Более
сложное квартетное туннельное расщепление уровней молекулы с двумя СН3-группами
[напр., (СН3)2СО] классифицируется по типам симметрии
прямого произведения
. Эта группа позволяет классифицировать вращат. уровни энергии молекул
типа симметричного волчка по квантовому числу К. Модельная симметрия
часто используется и для нежёстких молекул, когда нек-рые атомные группы
в молекуле имеют достаточно высокую симметрию, хотя сама молекула высокой
симметрии не имеет. Напр., если молекула содержит СН3-группу,
то при изучении внутр. вращения такой группы используется точечная группа
C3v. В частности, туннелирование группы СН3 в периодич. потенциальной
яме с тремя минимумами приводит к известному дублетному A- E-расщеплению
уровней по типам симметрии точечной группы
C3v. Более
сложное квартетное туннельное расщепление уровней молекулы с двумя СН3-группами
[напр., (СН3)2СО] классифицируется по типам симметрии
прямого произведения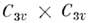

М Р Алиев
|
|