Симметрия кристаллов - свойство кристаллов совмещаться с собой
при поворотах, отражениях, параллельных переносах либо при части или комбинации
этих операций. Симметрия внеш. формы (огранки) кристалла определяется симметрией
его атомного строения, к-рая обусловливает также и симметрию физ. свойств
кристалла.

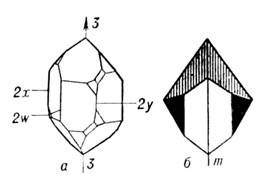
Рис. 1. а - кристалл кварца; 3 - ось симметрии 3-го порядка,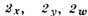 - оси 2-го порядка; б - кристалл водного метасиликата натрия; m - плоскость
симметрии.
- оси 2-го порядка; б - кристалл водного метасиликата натрия; m - плоскость
симметрии.
На рис. 1а изображён кристалл кварца. Внеш. его форма такова,
что поворотом на 120° вокруг оси 3 он может быть совмещён сам с
собой (совместимое равенство). Кристалл метасиликата натрия (рис. 1, б)преобразуется в себя отражением в плоскости симметрии m (зеркальное
равенство). Если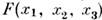 - функция, описывающая объект, напр. форму кристалла в трёхмерном пространстве
или к--л. его свойство, а операция
- функция, описывающая объект, напр. форму кристалла в трёхмерном пространстве
или к--л. его свойство, а операция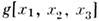 осуществляет преобразование координат всех точек объекта, то g является
операцией, или преобразованием симметрии, а F - симметричным объектом,
если выполняются условия:
осуществляет преобразование координат всех точек объекта, то g является
операцией, или преобразованием симметрии, а F - симметричным объектом,
если выполняются условия:
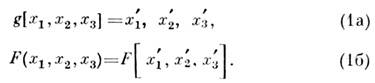
В наиб. общей формулировке симметрия - неизменность (инвариантность) объектов и законов при нек-рых преобразованиях описывающих их переменных. Кристаллы - объекты в трёхмерном пространстве, поэтому классич. теория симметрии кристаллов - теория симметричных преобразований в себя трёхмерного пространства с учётом того, что внутр. атомная структура кристаллов дискретная, трёхмерно-периодическая. При преобразованиях симметрии пространство не деформируется, а преобразуется как жёсткое целое. Такие преобразования паз. ортогональными или изометрическим и. После преобразования симметрии части объекта, находившиеся в одном месте, совпадают с частями, находящимися в др. месте. Это означает, что в симметричном объекте есть равные части (совместимые или зеркальные).
Симметрия кристаллов проявляется не только в их структуре и свойствах в реальном трёхмерном пространстве, но также и при описании энергетич. спектра электронов кристалла (см. Зонная теория ),при анализе процессов дифракции рентгеновских лучей, дифракции нейтронов и дифракции электронов в кристаллах с использованием обратного пространства (см. Обратная решётка)и т. п.
Группы симметрии кристаллов. Кристаллу может быть присуща не одна, а
неск. операций симметрии. Так, кристалл кварца (рис. 1, а)совмещается
с собой не только при повороте на 120° вокруг оси 3 (операция gi), но
и при повороте вокруг оси 3 на 240° (операция g2),
& также при поворотах на 180° вокруг осей 2Х, 2у,
2W (операции g3, g4, g5).
Каждой операции симметрии может быть сопоставлен элемент симметрии - прямая,
плоскость или точка, относительно к-рой производится данная операция. Напр.,
ось 3 или оси 2x, 2у, 2w являются
осями симметрии, плоскость т (рис. 1,б) - плоскостью зеркальной
симметрии и т. п. Совокупность операций симметрии {g1, g2,
..., gn} данного кристалла образует группу симметрии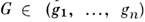 в смысле матем. теории групп. Последоват. проведение двух операций
симметрии также является операцией симметрии. В теории групп это обозначают
как произведение операций:
в смысле матем. теории групп. Последоват. проведение двух операций
симметрии также является операцией симметрии. В теории групп это обозначают
как произведение операций: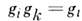 .
Всегда существует операция идентичности g0, ничего не
изменяющая в кристалле, наз. отождествлением, она геометрически соответствует
неподвижности объекта или повороту его на 360° вокруг любой оси. Число
операций, образующих группу G, наз. порядком группы.
.
Всегда существует операция идентичности g0, ничего не
изменяющая в кристалле, наз. отождествлением, она геометрически соответствует
неподвижности объекта или повороту его на 360° вокруг любой оси. Число
операций, образующих группу G, наз. порядком группы.
Группы симметрии преобразований пространства классифицируют: по числу
п измерений пространства, в к-рых они определены; по числу т измерений
пространства, в к-рых объект периодичен (их соответственно обозначают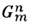 ),
и по нек-рым др. признакам. Для описания кристаллов используют различные
группы симметрии, из к-рых важнейшими являются точечные группы симметрии
),
и по нек-рым др. признакам. Для описания кристаллов используют различные
группы симметрии, из к-рых важнейшими являются точечные группы симметрии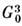 ,
описывающие внеш. форму кристаллов; их наз. также кристаллографич. классами;
пространственные группы симметрии
,
описывающие внеш. форму кристаллов; их наз. также кристаллографич. классами;
пространственные группы симметрии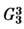 ,
описывающие атомную структуру кристаллов.
,
описывающие атомную структуру кристаллов.
Точечные группы симметрии. Операциями точечной симметрии являются:
повороты вокруг оси симметрии порядка N на угол, равный 360°/N (рис.
2, а); отражение в плоскости симметрии т (зеркальное отражение,
рис. 2, б); инверсия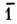 (симметрия относительно точки, рис. 2, в); инверсионные повороты
(симметрия относительно точки, рис. 2, в); инверсионные повороты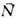 (комбинация поворота на угол 360°/N с одноврем. инверсией, рис.
2, г). Вместо инверсионных поворотов иногда рассматриваются эквивалентные
им зеркальные повороты
(комбинация поворота на угол 360°/N с одноврем. инверсией, рис.
2, г). Вместо инверсионных поворотов иногда рассматриваются эквивалентные
им зеркальные повороты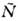 Геометрически возможные сочетания операций точечной симметрии определяют
ту или иную точечную группу симметрии, к-рая изображается обычно в стереографич.
проекции. При преобразованиях точечной симметрии по крайней мере одна точка
объекта остаётся неподвижной - преобразуется сама в себя. В ней пересекаются
все элементы симметрии, и она является центром стереографич. проекции.
Примеры кристаллов, относящихся к различным точечным группам, даны на рис.
3.
Геометрически возможные сочетания операций точечной симметрии определяют
ту или иную точечную группу симметрии, к-рая изображается обычно в стереографич.
проекции. При преобразованиях точечной симметрии по крайней мере одна точка
объекта остаётся неподвижной - преобразуется сама в себя. В ней пересекаются
все элементы симметрии, и она является центром стереографич. проекции.
Примеры кристаллов, относящихся к различным точечным группам, даны на рис.
3.
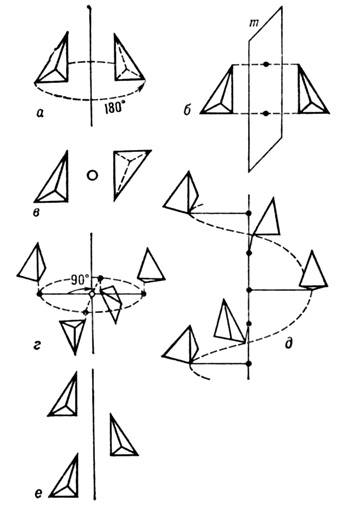
Рис. 2. Примеры операций симметрии: а - поворот; б - отражение; в - инверсия; г - инверсионный поворот 4-го порядка; д - винтовой поворот 4-го порядка; е - скользящее отражение.
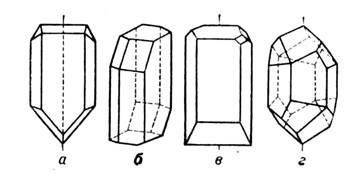
Рис. 3. Примеры кристаллов, принадлежащих к разным точечным группам
(кристаллографическим классам): а - к классу m (одна плоскость симметрии);
б - к классу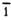 (центр симметрии или центр инверсии); а - к классу 2 (одна ось симметрии
2-го порядка); г - к классу
(центр симметрии или центр инверсии); а - к классу 2 (одна ось симметрии
2-го порядка); г - к классу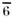 (одна инверсионно-поворотная ось 6-го порядка).
(одна инверсионно-поворотная ось 6-го порядка).
Точечные преобразования симметрии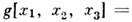
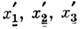 описываются линейными ур-ниями
описываются линейными ур-ниями
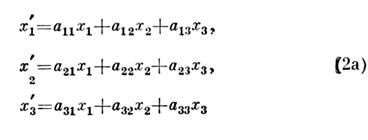
или матрицей коэффициентов
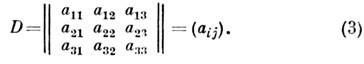
Напр., при повороте вокруг оси х1 на угол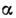 -
=360°/N матрица D имеет вид:
-
=360°/N матрица D имеет вид:
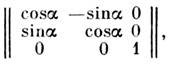
а при отражении в плоскости х1х2 D имеет
вид:

Число точечных групп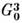 бесконечно. Однако в кристаллах ввиду наличия кристаллич. решётки возможны
только операции и соответственно оси симметрии до 6-го порядка (кроме 5-го;
в кристаллич. решётке не может быть оси симметрии 5-го порядка, т. к. с
помощью пятиугольных фигур нельзя заполнить пространство без промежутков).
Операции точечной симметрии и соответствующие им элементы симметрии обозначаются
символами: оси 1, 2, 3, 4, 6, инверсионные оси
бесконечно. Однако в кристаллах ввиду наличия кристаллич. решётки возможны
только операции и соответственно оси симметрии до 6-го порядка (кроме 5-го;
в кристаллич. решётке не может быть оси симметрии 5-го порядка, т. к. с
помощью пятиугольных фигур нельзя заполнить пространство без промежутков).
Операции точечной симметрии и соответствующие им элементы симметрии обозначаются
символами: оси 1, 2, 3, 4, 6, инверсионные оси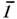 (центр
симметрии или центр инверсии),
(центр
симметрии или центр инверсии),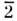 (она же - плоскость симметрии т),
(она же - плоскость симметрии т),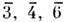 (рис. 4).
(рис. 4).
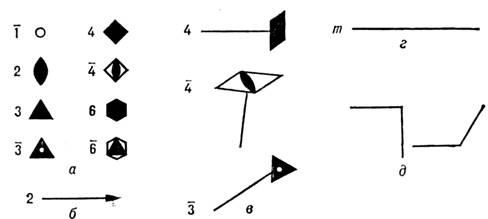
Рис. 4. Графические обозначения элементов точечной симметрии: а - кружок - центр симметрии, оси симметрии, перпендикулярные плоскости чертежа; б - ось 2, параллельная плоскости чертежа; в - оси симметрии, параллельные или косо расположенные к плоскости чертежа; г - плоскость симметрии, перпендикулярная плоскости чертежа; д - плоскости симметрии, параллельные плоскости чертежа.
Для описания точечной группы симметрии достаточно задать одну или неск.
порождающих её операций симметрии, остальные её операции (если они есть)
возникнут в результате взаимодействия порождающих. Напр., для кварца (рис.
1, а) порождающими операциями являются 3 и одна из операций 2, а всего
операций в этой группе 6. В международные обозначения групп входят символы
порождающих операций симметрии. Точечные группы объединяются по точечной
симметрии формы элементарной ячейки (с периодами а, Ь, с и углами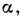
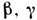 ) в 7 сингоний (табл. 1).
) в 7 сингоний (табл. 1).
Группы, содержащие кроме гл. оси N плоскости симметрии т, обозначаются как N/m, если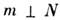 или Nm, если ось лежит в плоскости т. Если группа помимо
гл. оси имеет неск. проходящих через неё плоскостей симметрии, то она обозначается
Nmm.
или Nm, если ось лежит в плоскости т. Если группа помимо
гл. оси имеет неск. проходящих через неё плоскостей симметрии, то она обозначается
Nmm.
Табл. 1.-Точечные группы (классы) симметрии кристаллов
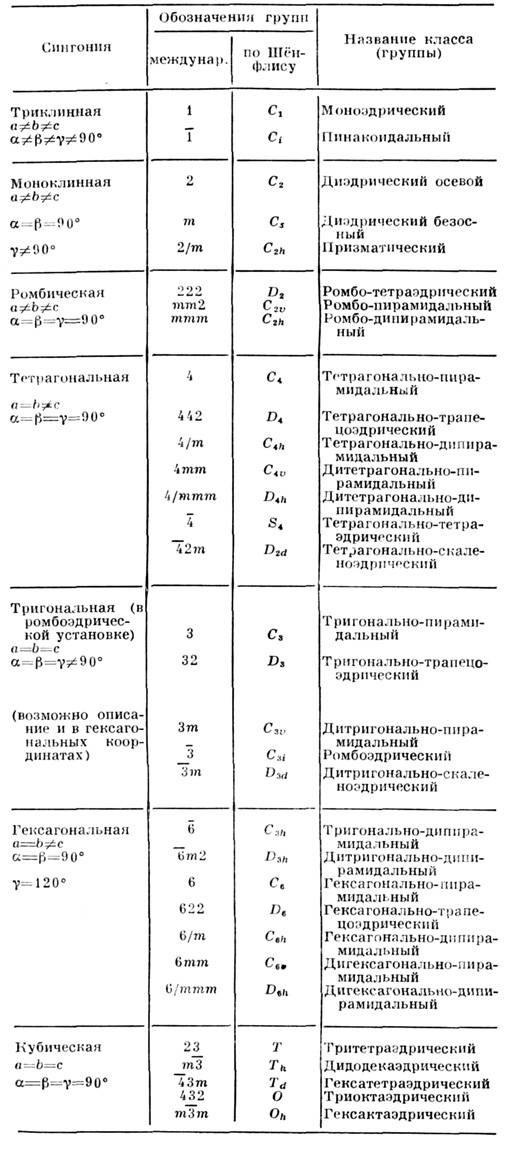
Группы, содержащие лишь повороты, описывают кристаллы, состоящие только из совместимо равных частей (группы 1-го рода). Группы, содержащие отражения или инверсионные повороты, описывают кристаллы, в К-рых есть зеркально равные части (группы 2-го рода). Кристаллы, описываемые группами 1-го рода, могут кристаллизоваться в двух энантиоморфных формах («правой» и «левой», каждая из к-рых не содержит элементов симметрии 2-го рода), но зеркально-равных друг другу (см. Энантиоморфизм).
Группы симметрии кристаллов несут в себе геом. смысл: каждой из операций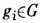 соответствует, напр., поворот вокруг оси симметрии, отражение в плоскости.
Нек-рые точечные группы в смысле теории групп, учитывающей лишь правила
взаимодействия операций
соответствует, напр., поворот вокруг оси симметрии, отражение в плоскости.
Нек-рые точечные группы в смысле теории групп, учитывающей лишь правила
взаимодействия операций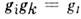 в данной группе (но не их геом. смысл), оказываются одинаковыми, или изоморфными
друг другу. Таковы, напр., группы 4 и
в данной группе (но не их геом. смысл), оказываются одинаковыми, или изоморфными
друг другу. Таковы, напр., группы 4 и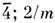 ,
тт2, 222. Всего имеется 18 абстрактных групп, изоморфных одной или
нескольким из 32 точечных групп симметрии кристаллов
,
тт2, 222. Всего имеется 18 абстрактных групп, изоморфных одной или
нескольким из 32 точечных групп симметрии кристаллов
Точечные группы описывают симметрию не только кристаллов, но любых конечных
фигур. В живой природе часто наблюдается запрещённая в кристаллографии
точечная симметрия с осями 5-го, 7-го порядка и выше. Для описания регулярной
структуры сферич. вирусов, в оболочках к-рых соблюдаются принципы плотной
укладки молекул, и нек-рых неорганич. молекул оказались важными икосаэдрич.
точечные группы 532 и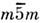 (см. Биологический кристалл ).Икосаэдрич. симметрия наблюдается
также в квазикристаллах.
(см. Биологический кристалл ).Икосаэдрич. симметрия наблюдается
также в квазикристаллах.
Предельные группы. функции, к-рые описывают зависимость различных свойств кристалла от направления, имеют определённую точечную симметрию, однозначно связанную с группой симметрии огра-нения кристалла. Она либо совпадает с ней, либо выше неё по симметрии (Неймана принцип).
В отношении макроскопич. свойств кристалл может описываться как однородная
непрерывная среда. Поэтому многие из свойств кристаллов, принадлежащих
к тем или иным точечным группам симметрии, описываются т. н. предельными
точечными группами, содержащими оси симметрии бесконечного порядка, обозначаемые
символом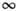 .
Наличие оси
.
Наличие оси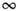 означает, что объект совмещается с собой при повороте на любой, в т. ч.
бесконечно малый, угол. Таких групп 7 (рис. 5). Т. о., всего имеется 32
+ 7 = 39 точечных групп, описывающих симметрию свойств кристаллов. Зная
группу симметрии кристаллов, можно указать возможность наличия или отсутствия
в нём нек-рых физ. свойств (см. Кристаллофизика).
означает, что объект совмещается с собой при повороте на любой, в т. ч.
бесконечно малый, угол. Таких групп 7 (рис. 5). Т. о., всего имеется 32
+ 7 = 39 точечных групп, описывающих симметрию свойств кристаллов. Зная
группу симметрии кристаллов, можно указать возможность наличия или отсутствия
в нём нек-рых физ. свойств (см. Кристаллофизика).
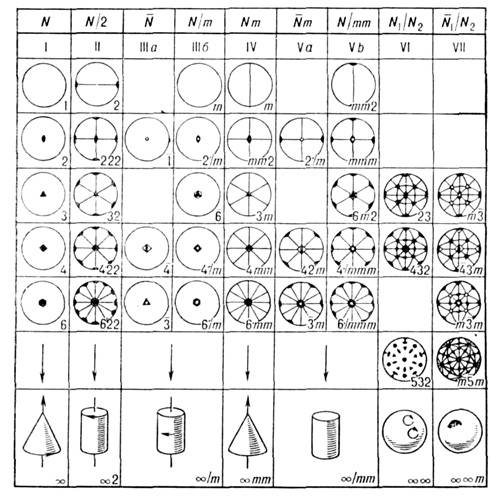
Рис. 5. Стереографические проекции 32 кристаллографических и 2 икосаэдрических групп. Группы расположены в колонки по семействам, символы которых даны в верхнем ряду. В нижнем ряду указана предельная группа каждого семейства и изображены фигуры, иллюстрирующие предельную группу.
Пространственные группы симметрии. Пространственная симметрия
атомной структуры кристаллов описывается пространственными группами симметрии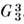 . Они наз. также фёдоровскими в честь нашедшего их в 1890 Е. С. Фёдорова;
эти группы были независимо выведены в том же году А. Шёнфлисом (A. Schoenflies).
В противоположность точечным группам, к-рые были получены как обобщение
закономерностей форм кристаллич. многогранников (С. И. Гессель, 1830, А.
В. Гадолин, 1867), пространственные группы явились продуктом математическо-геом.
теории, предвосхитившей эксперим. определения структуры кристаллов с помощью
дифракции рентг. лучей.
. Они наз. также фёдоровскими в честь нашедшего их в 1890 Е. С. Фёдорова;
эти группы были независимо выведены в том же году А. Шёнфлисом (A. Schoenflies).
В противоположность точечным группам, к-рые были получены как обобщение
закономерностей форм кристаллич. многогранников (С. И. Гессель, 1830, А.
В. Гадолин, 1867), пространственные группы явились продуктом математическо-геом.
теории, предвосхитившей эксперим. определения структуры кристаллов с помощью
дифракции рентг. лучей.
Характерными для атомной структуры кристаллов операциями являются 3
некомпланарные трансляции а, b, с, к-рые и задают трёхмерную
периодичность кристаллич. решётки. Кристаллич. решётка рассматривается
как бесконечная во всех трёх измерениях. Такое матем. приближение реально,
т. к. число элементарных ячеек в наблюдаемых кристаллах очень велико. Перенос
структуры на векторы а, Ь, с или любой вектор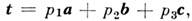 где p1, p2, р3 - любые целые числа,
совмещает структуру кристалла с собой и, следовательно, является операцией
симметрии (трансляционная симметрия).
где p1, p2, р3 - любые целые числа,
совмещает структуру кристалла с собой и, следовательно, является операцией
симметрии (трансляционная симметрия).
Физ. дискретность кристаллич. вещества выражается в его атомном строении.
Пространственные группы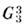 - это группы преобразования в себя трёхмерного однородного дискретного
пространства. Дискретность заключается в том, что не все точки такого пространства
симметрически равны друг другу, напр. атом одного и атом др. сорта, ядро
и электроны. Условия однородности и дискретности определяет тот факт, что
пространственные группы - трёхмерно периодические, т. е. любая группа
- это группы преобразования в себя трёхмерного однородного дискретного
пространства. Дискретность заключается в том, что не все точки такого пространства
симметрически равны друг другу, напр. атом одного и атом др. сорта, ядро
и электроны. Условия однородности и дискретности определяет тот факт, что
пространственные группы - трёхмерно периодические, т. е. любая группа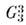 содержит подгруппу трансляций Т - кристаллич. решётку.
содержит подгруппу трансляций Т - кристаллич. решётку.
Вследствие возможности комбинирования в решётке трансляций и операций
точечной симметрии в группах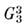 кроме операций точечной симметрии возникают операции и соответствующие
им элементы симметрии с трансляц. компонентой - винтовые оси различных
порядков и плоскости скользящего отражения (рис. 2, д, е).
кроме операций точечной симметрии возникают операции и соответствующие
им элементы симметрии с трансляц. компонентой - винтовые оси различных
порядков и плоскости скользящего отражения (рис. 2, д, е).
В соответствии с точечной симметрией формы элементарной ячейки (элементарного параллелепипеда) пространственные группы, как и точечные, подразделяются на 7 кристаллографических сингоний (табл. 2). Дальнейшее их подразделение соответствует трансляц. группам и соответствующим им Враве решёткам. Решёток Браве 14, из них 7 - примитивные решётки соответствующих сингоний, они обозначаются Р (кроме ромбоэдрической R). Другие-7 центриров. решёток: базо (боко) - центрированные А (центрируется грань bc), В (грань ас), С (аb); объёмноцентрнрованные I, гранецентрированные (по всем 3 граням) F. С учётом центрировки к оперирации трансляций t добавляются соответствующие центру центрирующие переносы tc. Если комбинировать друг с другом эти операции t + tс и с операциями точечных групп соответствующей сингоний, то получаются 73 пространственные группы, наз. симморфными.
Табл. 2.-Пространственные группы симметрии

На основе определённых правил из симморфных пространственных групп можно
извлечь нетривиальные подгруппы, что даёт ещё 157 несимморфных пространственных
групп. Всего пространственных групп 230. Операции симметрии при преобразовании
точки х в симметрично равную ей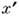 (а значит. и всего пространства в себя) записываются в виде:
(а значит. и всего пространства в себя) записываются в виде: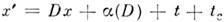 , где D - точечные преобразования,
, где D - точечные преобразования,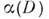 - компоненты винтового переноса или скользящего отражения,
- компоненты винтового переноса или скользящего отражения,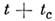 - операции трансляц. группы Браве. Операции винтовой симметрии и соответствующие
им элементы симметрии - винтовые оси имеют угл. компоненту
- операции трансляц. группы Браве. Операции винтовой симметрии и соответствующие
им элементы симметрии - винтовые оси имеют угл. компоненту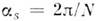 (N = 2, 3, 4, 6) и трансляционную ts = tq/N, где t - трансляция решётки, поворот на
(N = 2, 3, 4, 6) и трансляционную ts = tq/N, где t - трансляция решётки, поворот на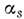 происходит одновременно с трансляцией вдоль оси Ж, q - индекс
винтового поворота. Общий символ винтовых осей Nq (рис.
6). Винтовые оси направлены вдоль гл. осей или диагоналей элементарной
ячейки. Оси 31 и 32, 41 и 43,
61 и 65, 62 и 64 соответствуют
попарно правым и левым винтовым поворотам. Кроме операции зеркальной симметрии
в пространственных группах возможны также плоскости скользящего отражения
а, Ь, с: отражение сочетается с переносом на половину соответствующего
периода решётки. Переносу на половину диагонали грани ячейки соответствует
т. н. клиноплоскость скольжения n, кроме того, в тетрагональных и кубич.
группах возможны «алмазные» плоскости d.
происходит одновременно с трансляцией вдоль оси Ж, q - индекс
винтового поворота. Общий символ винтовых осей Nq (рис.
6). Винтовые оси направлены вдоль гл. осей или диагоналей элементарной
ячейки. Оси 31 и 32, 41 и 43,
61 и 65, 62 и 64 соответствуют
попарно правым и левым винтовым поворотам. Кроме операции зеркальной симметрии
в пространственных группах возможны также плоскости скользящего отражения
а, Ь, с: отражение сочетается с переносом на половину соответствующего
периода решётки. Переносу на половину диагонали грани ячейки соответствует
т. н. клиноплоскость скольжения n, кроме того, в тетрагональных и кубич.
группах возможны «алмазные» плоскости d.
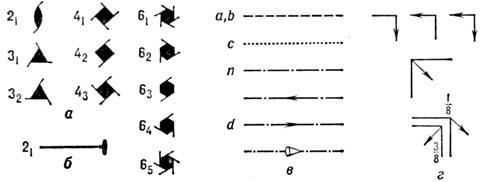
Рис. 6. а - Графические обозначения винтовых осей, перпендикулярных
плоскости рис.; б - винтовая ось, лежащая в плоскости рис.; в - плоскости
скользящего отражения, перпендикулярные плоскости рис., где а, b, с - периоды
элементарной ячейки, вдоль осей которой происходит скольжение (трансляционная
компонента а/2), п - диагональная плоскость скользящего отражения [трансляционная
компонента (а + b)/2], d - алмазная плоскость скольжения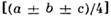 ; г - то же в плоскости рисунка.
; г - то же в плоскости рисунка.
В табл. 2 даны интернациональные символы всех 230 пространственных групп в соответствии с их принадлежностью к одной из 7 сингоний и классу точечной симметрии.
Трансляц. компоненты операций микросимметрии пространственных групп
макроскопически в точечных группах не проявляются; напр., винтовая ось
в огранке кристаллов проявляется как соответствующая по порядку простая
поворотная ось. Поэтому каждая из 230 групп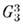 макроскопически
сходственна (гомоморфна) с одной из 32 точечных групп. Напр., на точечную
группу
макроскопически
сходственна (гомоморфна) с одной из 32 точечных групп. Напр., на точечную
группу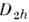 -
ттт гомоморфно отображаются 28 пространственных групп.
-
ттт гомоморфно отображаются 28 пространственных групп.
Обозначения Шёнфлиса пространственных групп - это обозначение соответственной
точечной группы (напр.,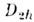 , табл. 1), к-рому сверху приписан принятый исторически порядковый номер,
напр.
, табл. 1), к-рому сверху приписан принятый исторически порядковый номер,
напр.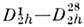 . В международных
обозначениях указывается символ решётки Браве и порождающие операции симметрии
каждой группы -
. В международных
обозначениях указывается символ решётки Браве и порождающие операции симметрии
каждой группы -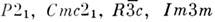 и т. д. Последовательность расположения пространственных групп в табл.
2 в международных обозначениях соответствует номеру (верхнему индексу)
в обозначениях Шёнфлиса.
и т. д. Последовательность расположения пространственных групп в табл.
2 в международных обозначениях соответствует номеру (верхнему индексу)
в обозначениях Шёнфлиса.
На рис. 7 дано изображение пространств. группы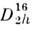 - Рпта согласно Интернациональным кристаллографич. таблицам. Операции
(и соответствующие им элементы) симметрии каждой пространственной группы,
указываемые для элементарной ячейки, действуют на всё кристаллич. пространство,
всю атомную структуру кристалла и друг на друга.
- Рпта согласно Интернациональным кристаллографич. таблицам. Операции
(и соответствующие им элементы) симметрии каждой пространственной группы,
указываемые для элементарной ячейки, действуют на всё кристаллич. пространство,
всю атомную структуру кристалла и друг на друга.
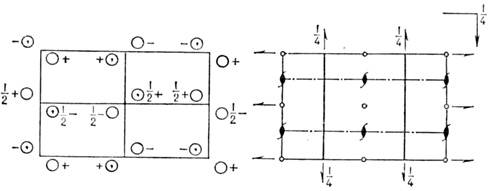
Рис. 7. Изображение группы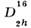 -
Рпта в Интернациональных таблицах.
-
Рпта в Интернациональных таблицах.
Если задать внутри элементарной ячейки к--н. точку х (x1x2x3), то операции симметрии преобразуют её в симметрично равные ей точки
во всём кристаллич. пространстве; таких точек бесконечное множество. Но
достаточно описать их положение в одной элементарной ячейке, и эта совокупность
уже будет размножаться трансляциями решётки. Совокупность точек, выводимых
из данной операциями gi группы G - х1,
x2,...,xn-1, наз. правильной системой точек (ПСТ).
На рис. 7 справа дано расположение элементов симметрии группы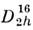 ,
слева - изображение ПСТ общего положения этой группы. Точки общего положения
- это такие точки, к-рые не расположены на элементе точечной симметрии
пространственной группы. Число (кратность) таких точек равно порядку группы.
Точки, расположенные на элементе (или элементах) точечной симметрии, образуют
ПСТ частного положения и обладают соответственной симметрией, количество
их в целое число раз меньше кратности ПСТ общего положения. На рис. 7 слева
кружками указаны точки общего положения, их внутри элементарной ячейки
8, символы «+» и «-», «1/2+» и «1/2-» означают соответственно координаты
+z, -z, 1/2 + z, 1/2 - z. Запятые пли их отсутствие означают попарное зеркальное
равенство соответствующих точек относительно плоскостей симметрии т, имеющихся
в данной группе при у = 1/4 и 3/4. Если же точка попадает на плоскость
т, то она этой плоскостью не удваивается, как в случае точек общего положения,
и число (кратность) таких точек частного положения 4, их симметрия -m.
То же имеет место при попадании точки в центры симметрии.
,
слева - изображение ПСТ общего положения этой группы. Точки общего положения
- это такие точки, к-рые не расположены на элементе точечной симметрии
пространственной группы. Число (кратность) таких точек равно порядку группы.
Точки, расположенные на элементе (или элементах) точечной симметрии, образуют
ПСТ частного положения и обладают соответственной симметрией, количество
их в целое число раз меньше кратности ПСТ общего положения. На рис. 7 слева
кружками указаны точки общего положения, их внутри элементарной ячейки
8, символы «+» и «-», «1/2+» и «1/2-» означают соответственно координаты
+z, -z, 1/2 + z, 1/2 - z. Запятые пли их отсутствие означают попарное зеркальное
равенство соответствующих точек относительно плоскостей симметрии т, имеющихся
в данной группе при у = 1/4 и 3/4. Если же точка попадает на плоскость
т, то она этой плоскостью не удваивается, как в случае точек общего положения,
и число (кратность) таких точек частного положения 4, их симметрия -m.
То же имеет место при попадании точки в центры симметрии.
Для каждой пространственной группы имеются свои совокупности ПСТ. Правильная система точек общего положения для каждой группы одна. Но нек-рые из ПСТ частного положения могут оказаться одинаковыми для различных групп. В Интернациональных таблицах указаны кратность ПСТ, их симметрия и координаты и все др. характеристики каждой пространственной группы. Важность понятия ПСТ состоит в том, что в любой кристаллич. структуре, принадлежащей данной пространственной группе, атомы или центры молекул располагаются по ПСТ (одной или нескольким). При структурном анализе распределение атомов по одной или неск. ПСТ данной пространственной группы производится с учётом хим. ф-лы кристалла и данных дифракц. эксперимента, позволяет находить координаты точек частных или общих положений, в к-рых расположены атомы. Поскольку каждая ПСТ состоит из одной или кратного числа решёток Браве, то и расположение атомов можно представлять себе как совокупность «вдвинутых друг в друга» решёток Браво. Такое представление эквивалентно тому, что пространственная группа содержит в себе как подгруппу трансляц. группу Браве.
Подгруппы групп симметрии кристаллов. Если часть операции к--л.
группы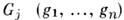 сама образует группу Gr(g1,...,gm),
сама образует группу Gr(g1,...,gm),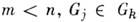 , то последняя наз. подгруппой первой. Напр., подгруппами точечной группы
32 (рис. 1, а) являются группа 3 и группа 2. Также и среди
пространств. групп существует иерархия подгрупп. Пространственные группы
могут иметь в качестве подгрупп точечные группы (таких пространственных
групп 217) и подгруппы, к-рые являются пространственными группами более
низкого порядка. Соответственно существует иерархия подгрупп.
, то последняя наз. подгруппой первой. Напр., подгруппами точечной группы
32 (рис. 1, а) являются группа 3 и группа 2. Также и среди
пространств. групп существует иерархия подгрупп. Пространственные группы
могут иметь в качестве подгрупп точечные группы (таких пространственных
групп 217) и подгруппы, к-рые являются пространственными группами более
низкого порядка. Соответственно существует иерархия подгрупп.
Большинство пространственных групп симметрии кристаллов различны между собой и как абстрактные группы; число абстрактных групп изоморфных 230 пространственным группам равно 219. Абстрактно равными оказываются 11 зеркально-равных (энантиоморфных) пространственных групп - одна лишь с правыми, другие с левыми винтовыми осями. Таковы, напр., P3121 и P3221. Обе эти пространственные группы гомоморфно отображаются на точечную группу 32, к к-рой принадлежит кварц, но кварц соответственно бывает правый и левый: симметрия пространственной структуры в этом случае выражается макроскопически, но точечная группа в обоих случаях та же.
Роль пространственных групп симметрии кристаллов. Пространственные группы симметрии кристаллов- основа теоретич. кристаллографии, дифракционных и иных методов определения атомной структуры кристаллов и описания кристаллич. структур.
Дифракционная картина, получаемая методом рентгенографии, нейтронографии или электронографии ,позволяет установить симметрийные и геом. характеристики обратной решётки кристалла, а следовательно и самой структуры кристалла. Так определяют точечную группу кристалла и элементарную ячейку; по характерным погасаниям (отсутствие определённых дифракционных рефлексов) определяют тип решётки Браве и принадлежность к той или иной пространственной группе. Размещение атомов в элементарной ячейке находят по совокупности интенсивностей дифракционных рефлексов.
Большую роль играют пространственные группы в кристаллохимии. Определено более 100 тыс. кристаллич. структур неорганич., органич. и биологич. соединений. Любой кристалл относится к одной из 230 пространственных групп. Оказалось, что почти все пространственные группы реализованы в мире кристаллов, хотя одни из них встречаются чаще, другие реже. Имеется статистика распространённости пространственных групп по различным видам хим. соединений. Пока не найдены среди исследованных структур лишь 4 группы: Рсс2, P42cm, P4nc1, Р6тп. Теория, объясняющая распространённость тех пли иных пространственных групп, учитывает размеры составляющих структуру атомов, понятия плотной упаковки атомов или молекул, роль «упаковочных» элементов симметрии - плоскостей скольжения и винтовых осей.
В физике твёрдого тела используется теория представлений групп с помощью матриц и спец. функций, для пространственных групп эти функции периодичны. Так, в теории структурных фазовых переходов 2-го рода пространственная группа симметрии менее симметричной (низкотемпературной) фазы является подгруппой пространственной группы более симметричной фазы и фазовый переход связан с одним из неприводимых представлений пространственной группы высокосимметричной фазы. Теория представлений позволяет также решать задачи динамики кристаллической решётки, её электронной и магн. структур, ряда физ. свойств. В теоретич. кристаллографии пространственные группы позволяют развить теорию разбиения пространства на равные области, в частности полиэдрические.
Симметрия проекций, слоев и цепей. Проекции кристаллич. структур
на плоскость описываются плоскими группами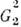 ,
их число - 17. Для описания трёхмерных объектов, периодических в 1 или
2 направлениях, в частности фрагментов структуры кристаллов, могут быть
использованы группы
,
их число - 17. Для описания трёхмерных объектов, периодических в 1 или
2 направлениях, в частности фрагментов структуры кристаллов, могут быть
использованы группы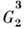 - двумерно периодические и
- двумерно периодические и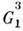 - одномерно периодические. Эти группы играют важную роль в изучении биологич.
структур и молекул. Напр., группы
- одномерно периодические. Эти группы играют важную роль в изучении биологич.
структур и молекул. Напр., группы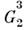 описывают
строение биологич. мембран, группы
описывают
строение биологич. мембран, группы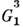 -
цепных молекул (рис. 8, а), палочкообразных вирусов, трубчатых кристаллов
глобулярных белков (рис. 8, б), в к-рых молекулы уложены согласно
спиральной (винтовой) симметрии, возможной в группах
-
цепных молекул (рис. 8, а), палочкообразных вирусов, трубчатых кристаллов
глобулярных белков (рис. 8, б), в к-рых молекулы уложены согласно
спиральной (винтовой) симметрии, возможной в группах (см. Биологический кристалл).
(см. Биологический кристалл).
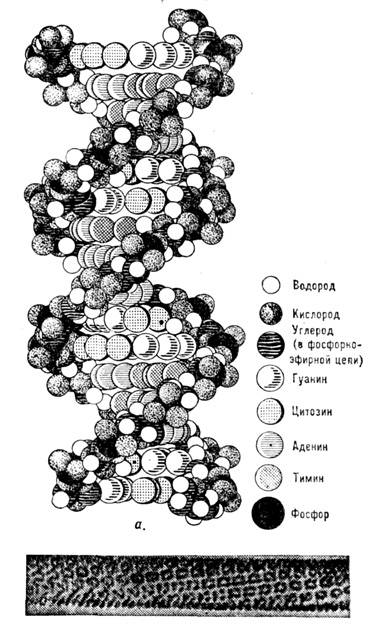
Рис. 8. Объекты со спиральной симметрией: а - молекула ДНК; б - трубчатый кристалл белка фосфорилазы (электронно-микроскопический снимок, увеличение 220 000).
Структура квазикристаллов. Квазикристалля (напр., А186Мn14) имеют икосаэдрич. точечную симметрию (рис. 5), к-рая невозможна в кристаллнч. решётке. Дальний порядок в квазикристаллах - квазипериодический, описываемый на основе теории почти периодич. функций. Структура квазикристаллов может быть представлена как проекция на трёхмерное пространство шестимерной периодич. кубич. решётки с осями 5-го порядка. Квазикристаллы с пятимерной симметрией в высшем измерении могут иметь 3 типа решёток Браве (примитивную, объёмноцентрированную и гранецентрированную) и 11 пространственных групп. Др. возможные типы квазикристаллов - укладки в стопку двумерных сеток атомов с осями 5-, 7-, 8-, 10-, 12-го ... порядков, с периодичностью вдоль третьего перпендикулярного сеткам направления.
Обобщённая симметрия. В основе определения симметрии лежит понятие
равенства (1,б) при преобразовании (1,а). Однако физически (и математически)
объект может быть равен себе по одним признакам и не равен по другим. Напр.,
распределение ядер и электронов в кристалле антиферромагнетика можно
описать с помощью обычной пространственной симметрии, но если учесть распределение
в нём магн. моментов (рис. 9), то «обычной», классич. симметрии уже недостаточно.
К подобного рода обобщениям симметрии относятся а н т и с и м м е т р и
я и цветная сниметрия.
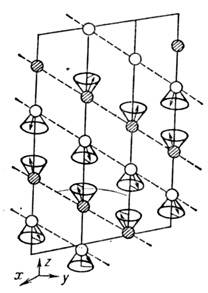
Рис. 9. Распределение магнитных моментов (стрелки) в элементарной ячейке ферримагнитного кристалла, описываемое с помощью обобщённой симметрии.
В антисимметрии в дополнение к трём пространственным переменным х1,
х2, х3 вводится добавочная, 4-я переменная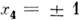 . Это можно истолковать таким образом, что при преобразовании (1,а) функция
F может быть не только равна себе, как в (1,б), но и «антиравна»
- изменит знак. Существует 58 групп точечной антисимметрии
. Это можно истолковать таким образом, что при преобразовании (1,а) функция
F может быть не только равна себе, как в (1,б), но и «антиравна»
- изменит знак. Существует 58 групп точечной антисимметрии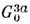 и 1651 пространственная группа антисимметрии
и 1651 пространственная группа антисимметрии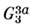 (шубнпковские
группы).
(шубнпковские
группы).
Если добавочная переменная приобретает не два значения, а больше (возможны 3,4,6,8, ..., 48), то возникает т. н. цветная симметрия Белова.
Так, известна 81 точечная группа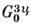 и 2942 группы
и 2942 группы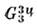 . Осн. приложения обобщённой симметрии в кристаллографии - описание магн.
структур.
. Осн. приложения обобщённой симметрии в кристаллографии - описание магн.
структур.
Найдены и др. группы антисимметрии (кратной и др.). Теоретически выведены и все точечные и пространственные группы четырёхмерного пространства и более высоких измерений. На основе рассмотрения симметрии (3 + К)-мерного пространства можно также описывать несоразмерные в трёх направлениях модулиров. структуры (см. Несоразмерная структура).
Др. обобщение симметрии - симметрия подобия, когда равенство частей
фигуры заменяется их подобием (рис. 10), криволинейная симметрия, статистич.
симметрия, вводимая при описании структуры разупорядоченных кристаллов,
твёрдых растворов, жидких кристаллов и др.

Рис. 10. Фигура, обладающая симметрией подобия.

Б. К. Вайнштейн
|
|