к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Квазикристалл

Квазикристалл - твёрдое тело, состоящее из атомов, к-рые не образуют кристаллич. решётки, но тем не менее обладают дальним координац. порядком, проявляющимся в способности когерентно рассеивать падающее излучение (см. Дальний и ближний порядок). Дальний координац. порядок принципиально отличает К. от жидкостей и аморфных тел, а отсутствие подрешеток - от таких нестехиометрич. соединений, как т. н. алхим. золото (Hg_3-_dAsF₆). Как и вещества с волнами зарядовой и спиновой плотности (см. Волны зарядовой плотности ),К. является несоразмерной структурой, однако в отличие от них несоизмеримость К. обусловлена свойствами его точечной группы симметрии. Характерными для К. являются нефёдоровские группы симметрии, несовместимые с трансляционной инвариантностью кристаллов (см. Симметрия кристаллов ).Известен ряд материалов, имеющих группу симметрии правильного икосаэдра, содержащую запрещённые для фёдоровских групп оси симметрии 5-го порядка. Эти вещества можно разделить на два класса: "метастабильные" (напр., Аl₆Мn, UPd₃Si, Ti-Ni - V) и "стабильные" (напр., Al₆CuLi₃, Al-Сu-Fe, Al-Zn-Mg). Метастабильные К. получаются из расплава быстрым охлаждением, а при нагревании необратимо переходят в кристаллич. состояние. Электронограмма этих К. состоит из точечных рефлексов (рис. 1), характерных для обычных кристаллов (см. Электронография).

Рис. 1. Электронограмма квазикристалла Аl₆Мn.

Размер области, в к-рой имеется дальний координац. порядок, оценивается по обратной полуширине дифракционных пиков и для разных соединений составляет от 10 до 10³Е. Стабильные К. получаются при сколь угодно медленном охлаждении расплава, т. е. ему соответствует определённая область на диаграмме равновесных состояний. Дифракционные пики электронограммы имеют малую ширину, варьирующуюся от 10^-2 до 10^-5Е, т. е. размер области координац. упорядочения существенно больше, чем у метастабильных К. Как и для обычных кристаллов, группа симметрии проявляется в морфологии роста, приводя к образованию огранённых монокристаллов с икосаэдрич. симметрией (рис. 2). Помимо икосаэдрич. К., получены также К., группы симметрии к-рых содержат оси симметрии 8-го, 10-го и 12-го порядка, запрещённые для фёдоровских групп симметрии.

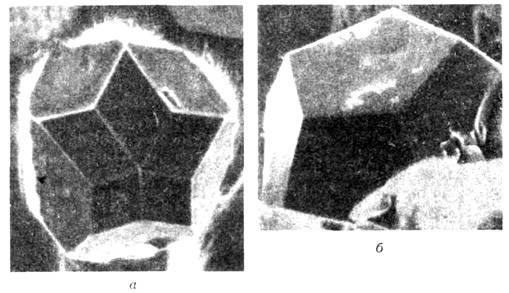
Рис. 2. Огранённые монокристалличесиие зёрна икосаэдрических К.: a) Al₆Cu Li₃-триаконтаэдрическая огранка; 6) А1-Сu-Fe - додекаэдрическая огранка.

Структуру икосаэдрич. К. можно описать двумя эквивалентными способами. Первый основывается на предложенном Р. Пенроузом (R. Penrose) методе построения непериодич. узоров, состоящих из двух разных элементов (рис. 3). Хотя у этого узора и его трёхмерного аналога, описывающего К., периодичность отсутствует, в расположении ромбов и соответствующих им атомов есть элементы упорядочения: 1) в узоре можно найти сколь угодно большие фрагменты с симметрией 5-го порядка; 2) структура квазипериодична - на достаточно больших расстояниях повторяются сколь угодно большие её участки; 3) узор обладает симметрией подобия - структура, получаемая удалением определ. набора атомов, отличается от исходной изменением масштаба в t=[(Ц5)+l]/2 раз; 4) атомы расположены в определённых плоскостях (в двумерном случае - на линиях), причём расстояние между плоскостями (линиями) может принимать 2 значения, к-рые чередуются в определённом порядке (связанном с числовым рядом Фибоначчи), отношение этих значений равно t;

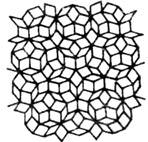
Рис. 3. Плоский непериодический узор, составленный из двух типов ромбов с острыми углами 36° и 72°.

5) дифракц. картина от подобной структуры необычна: расположение атомов вдоль плоскостей приводит к Брэгговским пикам, причём, в отличие от кристаллов, точечные рефлексы плотно заполняют обратное пространство, тем не менее только малая доля пиков имеет большую интенсивность и может наблюдаться экспериментально. Положения пиков и распределение их интенсивностей, вычисленные для трёхмерного узора, качественно согласуются с экспериментом. Др. метод описания структуры икосаэдрич. К. основан на том, что группа икосаэдра содержится в группе симметрии шестимерного гиперкуба, к-рая совместима с трансляционной инвариантностью в шестимерном пространстве. Произвольный шестимерный периодич. кристалл с такой симметрией может быть использован для построения трёхмерной структуры. Для этого трёхмерное пространство рассматривается как гиперплоскость в шестимерном и часть атомов шестимерного кристалла, близкая к ней, проектируется на гиперплоскость. Изменяя шестимерный кристалл, можно получить различные трёхмерные структуры и, в частности, узор Пенроуза. Полученные т. о. структуры обладают свойствами 1-5. Выбор пространства др. размерности и гиперплоскости в нём позволяет описать структуры с произвольными нефёдоровскими симметриями.

Литература по квазикристаллам

Shechtman D. и др., Metallic phase with longrange orientation order and no translational symmetry, "Phys. Rev. Lett.", 1984, v. 53, p. 1951;
Levine D., Steinhardt P. J., Quasicrystals: a new class of ordered structures, там же, р. 2477;
Калугин П. А., Китаев А. Ю., Левитов Л. С., Аl_0,86Mn_0,14 - шестимерный кристалл, "Письма в ЖЭТФ", 1985, т. 41, с. 119.

Л. С. Левитов

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что "тёмная материя" - такая же фикция, как черная кошка в темной комнате. Это не физическая реальность, но фокус, подмена.
Реально идет речь о том, что релятивистские формулы не соответствуют астрономическим наблюдениям, давая на порядок и более меньшую массу и меньшую энергию. Отсюда сделан фокуснический вывод, что есть "темная материя" и "темная энергия", но не вывод, что релятивистские формулы не соответствуют реалиям. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира